Thermally Radiative Viscous Fluid Flow Over Curved Moving Surface in Darcy-Forchheimer Porous Space
A.Rauf∗Z.Abbas S.A.Shehzad and T.Mushtaq
1Department of Mathematics, The Islamia University of Bahawalpur, Bahawalpur, 63100 Pakistan
2Department of Mathematics, COMSATS University Islamabad, Sahiwal 57000, Pakistan
3Department of Mathematics, COMSATS University Islamabad, Vehari 61100, Pakistan
(Received July 31, 2018; revised manuscript received August 19, 2018)
Abstract A numerical analysis is developed for incompressible hydromagnetic viscous fluid passed through a curved stretching surface.Fluid saturated by porous space is bounded by curved surface.Term of porous medium is characterized by implementation of Darcy-Forchheimer theory.Adequate similarity variables are implemented to develop a system of non-linear ordinary differential system of equations, which govern the flow behavior.The impact of radiation constraint and Eckert number is incorporated in the energy equation.Numerical scheme based on RKF45 technique is implemented to solve the derived flow model.Prescribed heat flux (PHF)and prescribed surface temperature (PST)boundary conditions are utilized on temperature with Prescribed Surface Concentration (PSC)and Prescribed Mass Flux (PMF)on concentration.Flow behavior is discussed for both the slip and no-slip conditions.Dimensionless physical quantities are presented through graphs and tables.
Key words: viscous fluid, porous medium, curved stretching sheet, radiation, Joule heating

Nomenclature
1 Introduction
Cooling of filaments or continuous strips, paper production, metallic plate cooling placed in cooling bath,glass blowing, artificial fibers, wire drawing and extrusion of rubber sheets are some practical applications of fluid flow passing through stretching surfaces.Polymer industry plays a major role in the process of molten polymers manufacturing with the help of slit die for the production of plastic or fiber sheet.Such materials travelled between wind-up and feed roll or through conveyor-belts describing the behavior of stretched surfaces.[1]The mechanical characteristics of the product strictly depend on the heat transfer rate through stretching surfaces.Boundary layer approximation is used for the solutions and hence not comprises the exact solution of Navier-Stokes equation.[2−3]However Crane[4]presented a similarity solution in closed and exact form for viscous fluid owing to a linear stretching surface.Many researchers extended the Crane’s idea by including different physical features like injection/suction, magnetic field, analysis of heat transfer etc.The combined influence of mass and heat transport analysis was presented by Gupta and Gupta[5]over porous stretched surface considering the injection/suction cases.Wang[6]investigated viscous flow through a stretched surface in view of suction and surface slip.The flow analysis of micropolar fluid past through stretching/shrinking surface was analyzed by Zhenget al.[7]Unsteady boundary layer viscous fluid problem corresponding to a stretching sheet was discussed by Rashidi and Pour.[8]Sheikholeslamiet al.[9]reported the flow problem of nanofluid past stretched wall.Many researchers investigated different flow models along flat surfaces.[10−14]
The flows embedded in porous medium generated a remarkable interest between the scientists owing to their wide practical applications in industry such as geothermal systems, porous insulation, packed beds, fossil fuels, extraction of crude oils, food storage, petroleum technology and disposal of waste materials etc.[15−17]Different models like Darcy and Brinkman, and Darcy-Forchheimerextended was presented in literature to explain physical and mathematical features in the porous medium.Researchers are curious to study the models related to porous media.Such models are developed in view of Darcy’s law in which pressure gradient is in direct relationship with volume average velocity.Darcy’s formula is capable for slower velocity and lesser porosity while excluding the influence of thermal dispersion, inertia forces,variable porosity and solid boundary.The addition of non-Darcian impacts is very essential in the analysis of porous medium in order to achieve the desired accurate results.Such impacts are introduced by Forchheimer[18]with the addition of the term named square velocity in the term of Darcian-velocity.After that Muskat[19]named such term as “Forchheimer term” which is applicable for high Reynolds number.Seddek[20]reported the analysis of thermophoretic velocity effect in Darcy-Forchheimer porous space by considering the convective flow of viscous liquid.Pal and Mandal[21]considered the convective diffusion in hydromagnetic viscous fluid flow in a non-Darcy porous space under the aspects of heat sink/source.Gireeshaet al.[22]addressed the numerical modeling of boundary layer liquid through non-Darcian effects.
In all the work cited above authors considered flow models over flat surfaces.Cartesian co-ordinates are implemented for the modeling of the problem.Fluid passed through curved moving surfaces has practical implications in stretch-forming machines owing to curve jaws.A numerical problem of viscous fluid by curved stretched surface was first discussed by Sajidet al.[23]Curvilinear coordinates were utilized for the governing equations.Later Sajidet al.[24]extended his work to the flow of micropolar fluid through curved sheet.The results show that pressure can not be neglected within the boundary layer in contrast with the flat stretching surface.The same problem was modified by Naveedet al.[25]by considering the phenomenon of heat transportation.Naveedet al.[26]reported the unsteady hydromagnetic flow of viscous fluid through a curved surface.Buongiorno model was implemented to find the numerical solution of curved sheet problem by Naveedet al.[27]Rosca and Pop[28]studied flow of unsteady viscous fluid by curved stretching/shrinking sheet.Imtiazet al.[29]analyzed analytically unsteady hydromagnetic viscous fluid through curved sheet.A numerical problem of viscous fluid owing to non-linear stretched curved sheet was constructed by Sanniet al.[30]Abbaset al.[31]reported the flow model of viscous liquid.
The combined influence of heat with mass transfer over flat surfaces has gained considerable interest among the researches due to its significance importance in chemical industries and metallurgy like polymer extrusion, continuous casing,metal spinning,food processing,temperature distribution to agriculture fields and flow in desert cooler.More importantly polymer industry has main operation of extrusion of plastic sheets.The process involves the transfer of heat between surrounding fluid and the surface.Melt issue from slit is expanded in order to acquire the required quality in manufacturing process of sheet.Thermal radiative flow is important for industrial purposes such as nuclear plant, air craft, design of equipments, gas turbines, space vehicles, satellite etc.In the perspective of space machinery, few devices are produced to function at large temperature for the achievement of higher thermal efficiency.Hence radiation impact is very important in the process of high temperature while studding the thermal effects.Rashidiet al.[32]investigated hydromagnetic viscous fluid flow problem due to a vertical sheet incorporating the influence of radiative heat with mass transfer.Rashidiet al.[33]reported the problem of thermally radiative nanofluid due to stretched surface.Palet al.[34]discussed the influence of thermal radiation in nanofluids through stretching/shrinking surface.A numerical study on three dimensional nanofluid flow through stretching sheet under solar radiation was examined by Raufet al.[35]Hayatet al.[36]reported the thermal radiation effect on Maxwell nanofluid flow passed through a stretching surface.
The intention of the current study is to elaborate the numerical outcomes of thermally radiative flow of hydromagnetic viscous fluid subject to the stretching surface with mass transfer.The stretching surface is drenched into non-Darcy permeable medium.Prescribed heat and mass flux conditions on temperature and concentration with slip and no-slip conditions on velocity are utilized.The results are also discussed for prescribed surface temperature and concentration cases.According to the authors’ knowledge, till now no such study is reported in the literature.Problem formulation is illustrated in Sec.2.Numerical scheme is prescribed in Sec.3.Section 4 has the detailed discussion of the results obtained through numerical technique.In Sec.5 we presented the concluding remarks the current research.
2 Problem Formulation
We consider incompressible radiative two dimensional MHD flow of viscous fluid over a stretched curved surface with radiusR.The surface is submerged in the non-Darcy porous medium.Ther-axis is taken normal to the direction of flow.To make the sheet stretched, we apply opposite forces of same magnitude at the ends of curved surface alongs-direction by fixing the origin.A magnetic field with magnitudeB0is functional along transverse direction as mentioned in Fig.1.The magnetic Reynolds number Re is specified to be less as a result the induced magnetic field is insignificant.Electric field is not considered.Governing equations of flow phenomenon are[31]

here (u,v)denote the components of velocity along (s,r)-directions respectively,ρthe liquid density,pthe pressure,σethe electric conductivity,cbthe form of drag,ϕ1andk1are the porosity and permeability of porous medium,respectively,DBthe diffusion co-efficient,Tthe temperature,Cthe concentration,qrthe radiative heat flux andµthe dynamic viscosity.

Fig.1 Flow configuration.
The suitable conditions suggested for the flow problem are:[37]
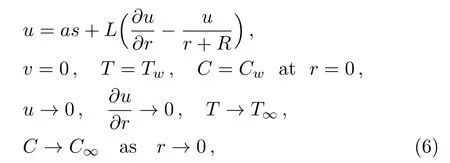
hereastands for constant of stretching andLthe slip parameter initial value.WhenL= 0,no-slip condition case can be retrieved.For different heating processes, we have:[31]
Case 1PHF and PMF
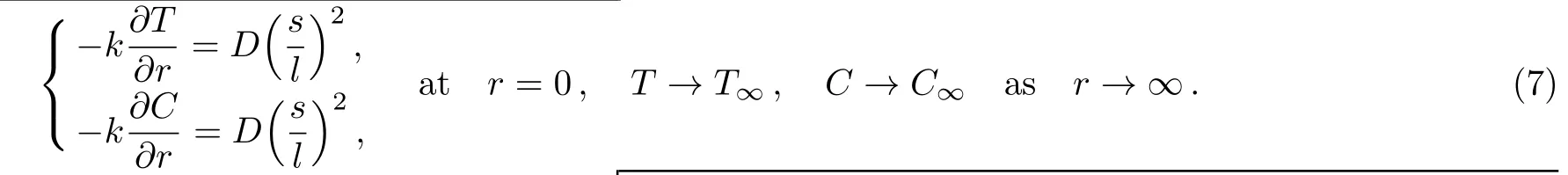
Case 2PST and PSC

For finding the solution of Eqs.(2)–(5),the following similarity variables are utilized:
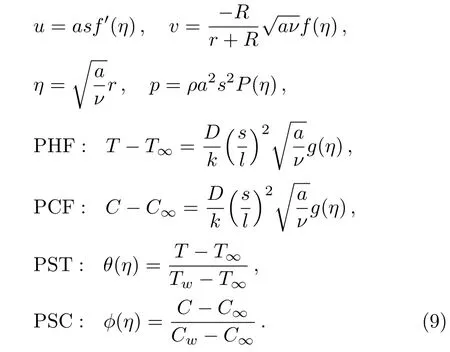
The continuity equation (1)is automatically satisfied by using the similarity transformation.The transformed equations (2)and (3)are:



Equations (4)and (5)take the following form:
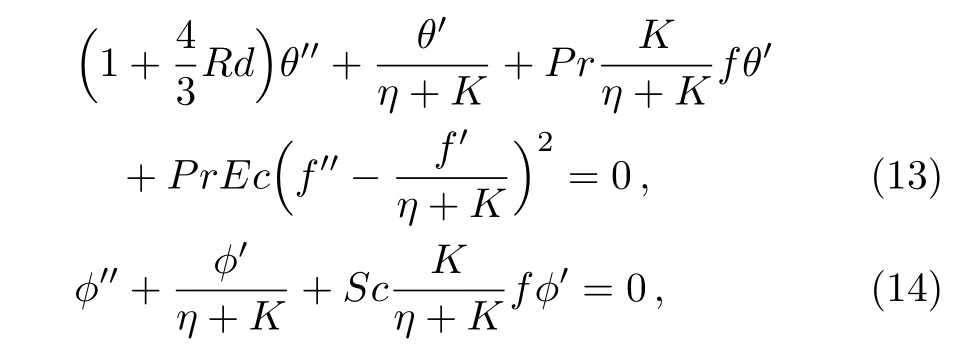
herePr=µcp/kthe Prandtl number,Rd=16σthe radiation parameter,Sc=ν/DBthe Schmidt number andEc=a2l2/Acpthe Eckert number in whichAis constant.The transformed boundary conditions (6)–(8)are as follows:
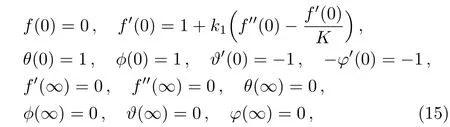
wherek1=L(a/ν)1/2is the slip length and the slip condition can be obtained fork1=0.
The physical quantities of our interest are the skin friction co-efficient, local Nusselt number and Sherwood number along s-directions, which take the following form:
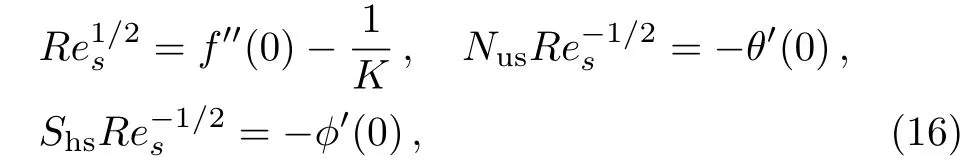
whereRes=as2/νis the local Reynolds number.
3 Numerical Scheme
Runge-Kutta-Fehlberg fourth fifth order (RKF45)technique, mainly based on the numerical method that is helpful for the solution of the equation dy/dx=h(x,y),y(xs)=ys.In this technique appropriate step-size is used and technique ensures accuracy in the solution of initial value problem.Every proper step-size contains two dissimilar approximations to solution that are computed and then compared.Valid approximation is considered when the answers are close enough.In vice versa case the stepsize is reduced to obtain the desired accuracy.The addition in step-size is made in the scenario is answers meet the criteria of more than significant digits.The required six steps are:


Order 4 approximation to the solution is:
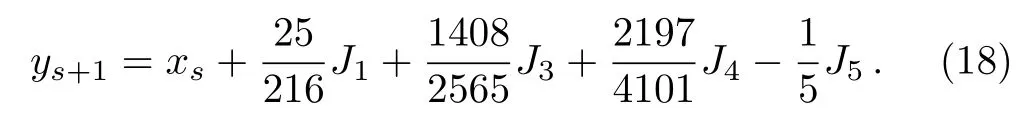
A better order 5 approximation to the solution is:
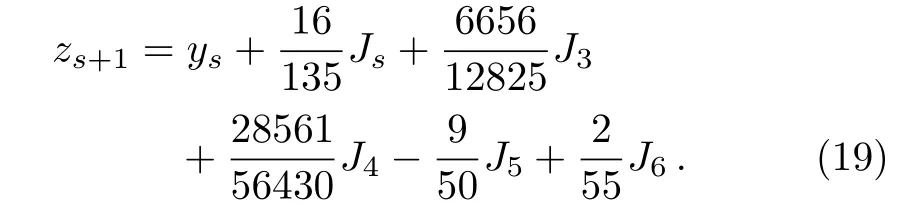
Finallydhis optimal step size which is defined by multiplying scalardwithh,wheredis obtained by the formula:

where tol is for error tolerance.
Our key objective is to transform first the system(11)–(15)into initial value problem.To do this, we set:
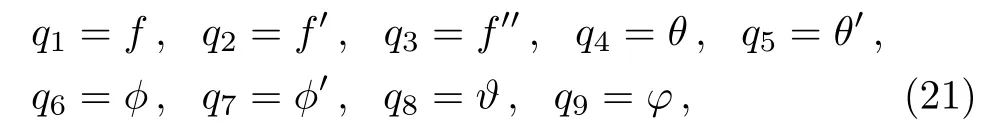
here prime denotes the derivative with respect toη.Using Eq.(21)into Eqs.(11)–(15), we acquired the reduced system of first order equations:

Boundary conditions (15)become:
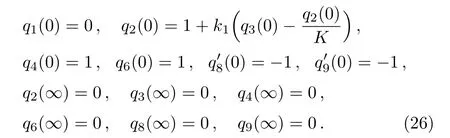
The criterion for convergence is settled to 10−7at least.
4 Results and Discussion
We studied the two-dimensional viscous fluid flow over a curved sheet.We implement Runge-Kutta-Fehlberg forth-fifth (RKF45)order technique[34]to obtain a numerical solution of Eqs.(12)–(14)subject to boundary conditions (15).This technique transformed the boundary value problem to initial one and guarantees the accurateness in the solution.In numerical procedure we fixηmax= 5, 15, 25 to achieve an asymptotic behavior of flow parameters.[10]Dimensionless parameters are discussed through graphs and tables for better understanding of the physics of problem.
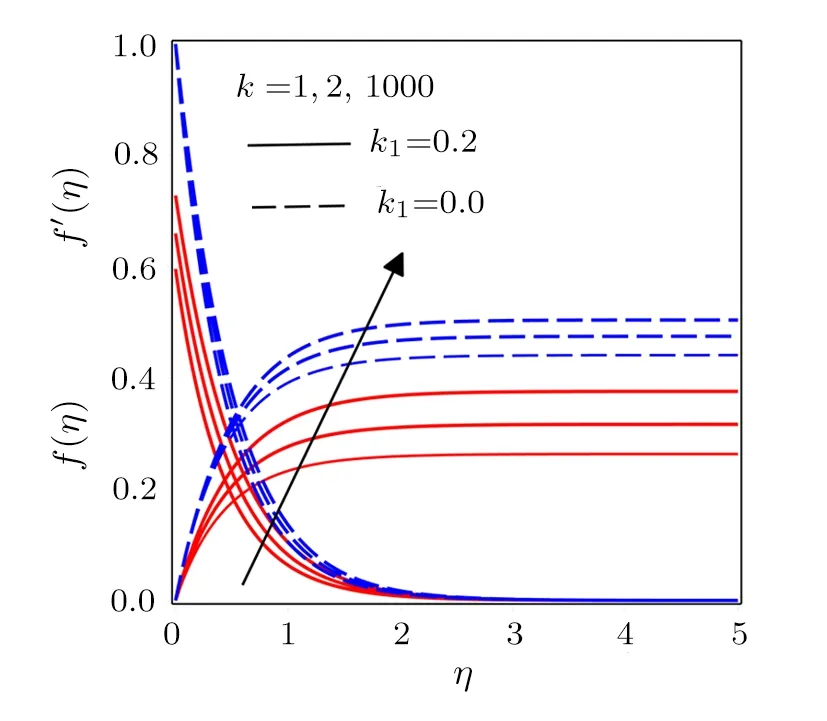
Fig.2 Influence of various values of k on f(η)and f′(η)with k1=0.2 and k1=0.

Fig.3 Influence of various values of p1 on f(η)and f′(η)with k1=0.2 and k1=0.
Figure 2 is plotted to show the impact of curvature radius parameterkon velocity profiles fork1= 0 andk1= 0.2.The casesk1= 0 andk1= 0.2 in Eq.(15)show no-slip and slip conditions respectively.Both the profilesf′(η)andf(η)correspond to theuandvcomponents of velocity are enhanced for increasing values ofk.Actually radius of the sheet increases for larger values of the curvature parameter which accelerates the fluid flow.Figure 3 is drawn to study the behavior of porosity parameter.The existence of porous medium slows down the flow field, which in results increase the shear stress at the curved surface and so the velocity profiles show a decreasing tendency for increasing values ofP1.Opposite to the impact of porosity parameter, the variations in the local inertia co-efficient parameter lead to enhance the profilesf(η)andf′(η)as presented in Fig.4.

Fig.4 Influence of various values of α on f(η)and f′(η)with k1=0.2 and k1=0.
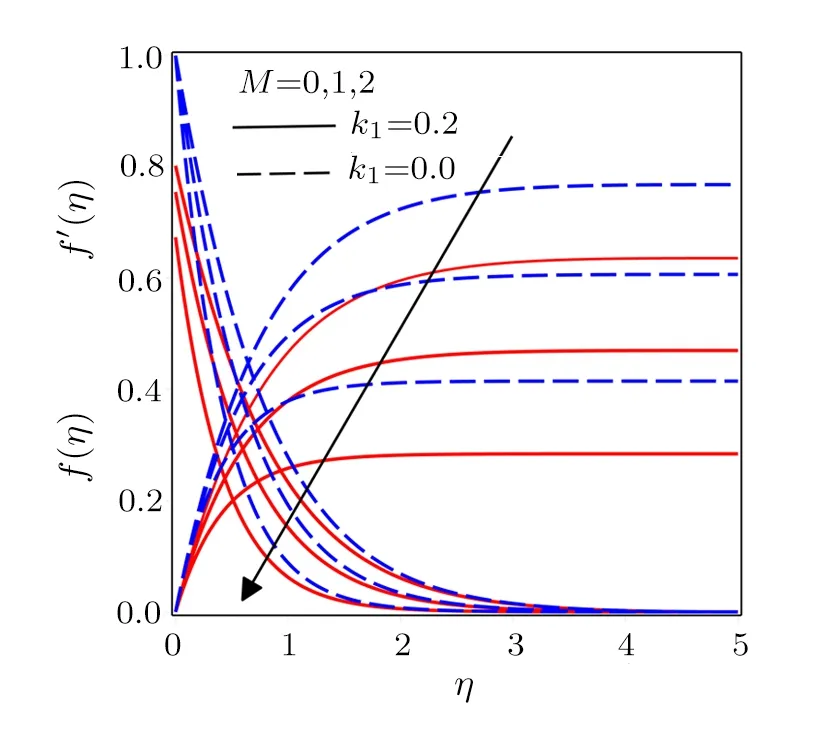
Fig.5 Influence of various values of M on f(η)and f′(η)with k1=0.2 and k1=0.
Figure 5 illustrates the variations in velocity profiles for enhancing magnetic parameter.The strength of applied magnetic force produces larger Lorentz force.Such force suppresses the fluid flow motion that caused a decreasing nature of velocity profiles.It is seen that velocity boundary layer thickness shows an increasing tendency in Figs.2 and 4 while a reverse phenomenon is noted from Figs.3 and 5.Temperature profilesθ(η)andϑ(η)and concentration profilesϕ(η)andφ(η)are drawn for PST and PHF cases in Figs.6–9.Figure 6 is plotted to observe the influence of Prandtl number.Increasing values ofPrreduces the thermal diffusivity, which in results decreases the temperature and its related thermal boundary layer thickness.

Fig.6 Influence of various values of Pr for different conditions PHF and PST.
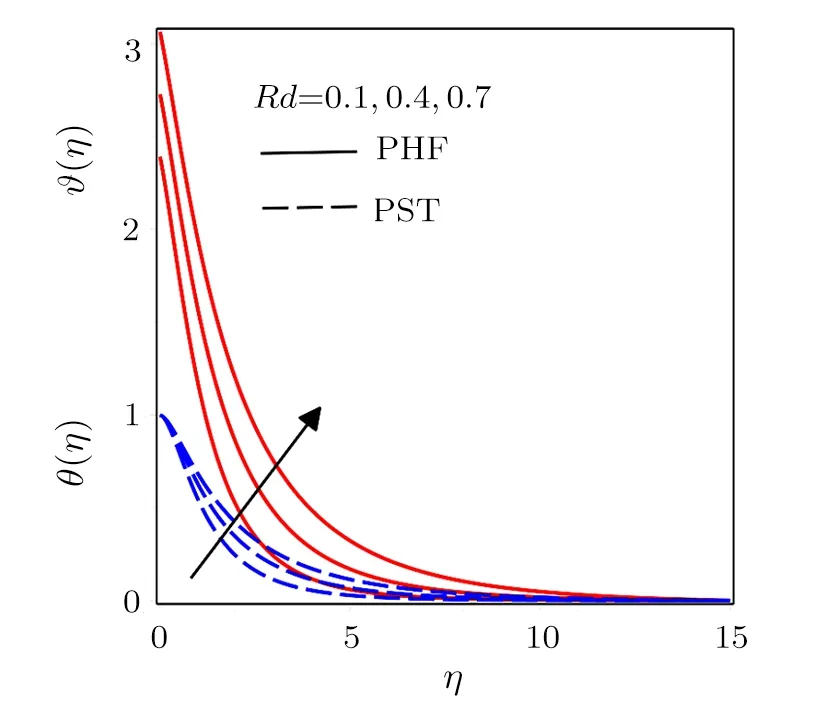
Fig.7 Influence of various values of Rd for different conditions PHF and PST.
Figure 7 exposes the variations of radiation parameter.Conduction effects increases for different values ofRdand consequently due to diffusion flux temperature amplify with its associated boundary layer thickness.Figure 8 is designed to explore the effects of Eckert number.Heat produces in the fluid flow from frictional heating by increasingEc, which causes an increase in temperature distribution with thermal boundary layer thickness.Mass diffusion decreases for larger values of Schmidt number ultimately shows a reduction in concentration profiles and boundary layer thickness as presented in Fig.9.Figures 10 and 11 depict the variations inP(η)for higher values ofkandα.A decrease in the magnitude of pressure inside boundary layer is noticed for increasing values of radius of curvature parameter and local inertia coefficient parameter.Moreover for away from sheet the pressure distribution approaches to zero.Figures 12 and 13 exhibit pressure distribution for various values porosity parameter and magnetic parameter.Initially magnitude of pressure decreases and afterη >1 a reverse trend in pressure distribution is noted by increasingP1andM.

Fig.8 Influence of various values of Ec for different conditions PHF and PST.

Fig.9 Influence of various values of Sc for different conditions PHF and PST.
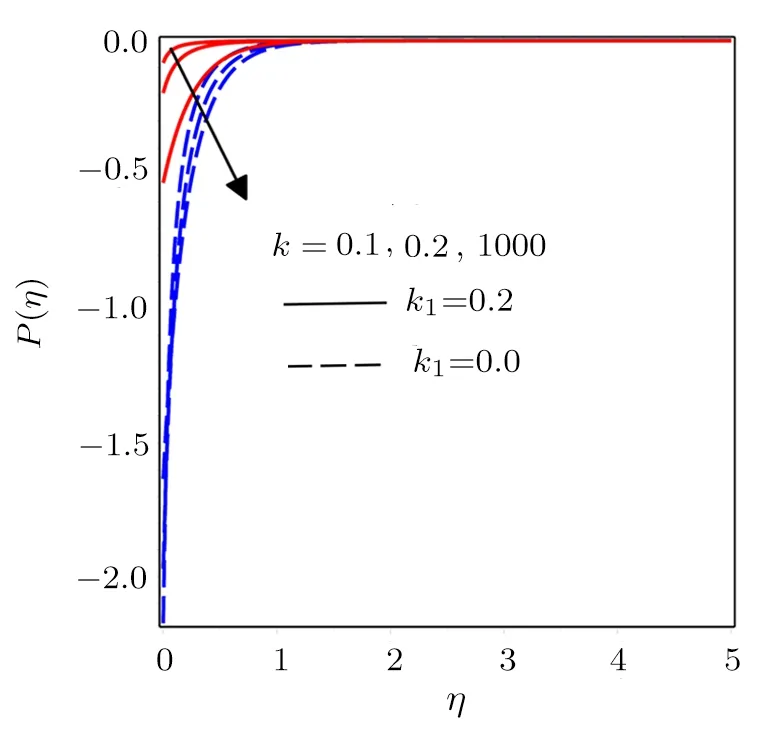
Fig.10 Influence of various values of k on P(η)with k1=0.2 and k1=0.

Table 1 Shear stress at sheet for various values of K,p1,α,and M at different conditions k1=0.2 and k1=0.
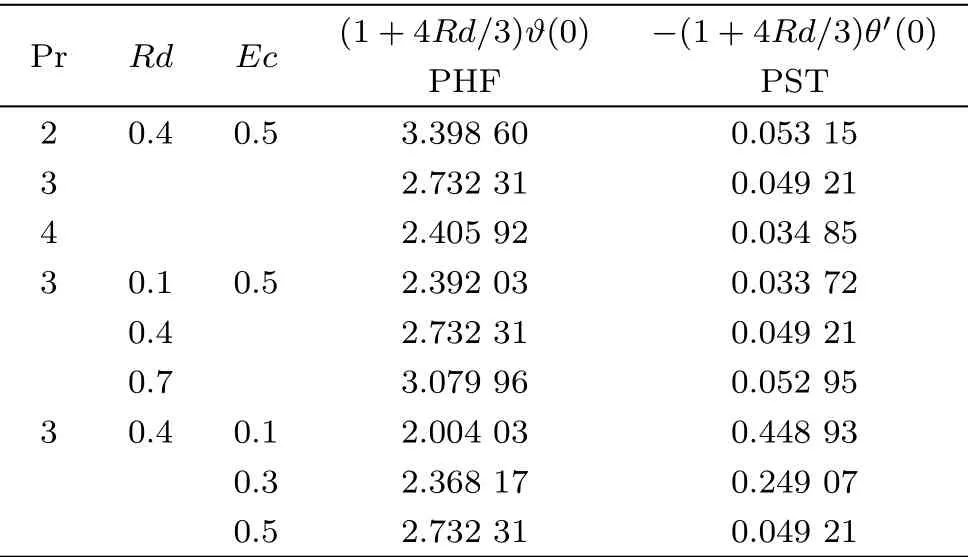
Table 2 Heat transfer rate at sheet for various values of Pr, Rd, and Ec at different conditions PHF and PST.

Table 3 Mass transfer rate at sheet for various values of Sc at different conditions PMF and PSC.

Table 4 Relative values of −CfRe1/2s when P1=α=0,M=0.2, and k1=0.
Table 1 illustrates the impact ofK,P1,αandMat two different conditionsk1=0.2 andk1=0.Shear stress are enhanced due to larger values of porosity parameter and magnetic parameter while an opposite trend in the values of shear stress are noticed for different values ofKandM.Heat transfer rate for various values of Prandtl number, radiation parameter and Eckert number at different conditions PHT and PST is shown in Table 2.A decrement in transfer rates are observed for enhancing values ofPrwhile the influence of radiation parameter differ from that of the Prandtl number.An increasing tendency in heat transfer rate is eminent for arbitrary values of Eckert number in case of PHT whereas an opposite scenario is observed for PST.Various values of Schmidt number decrease mass transfer rate when considering PHC and a reverse behavior due to PSC as shown in Table 3.Table 4 is drawn to for the validation of present work with the previously published literature in a limiting case by varyingKto compute skin-friction co-efficient.The obtained results match well with Ref.[31].
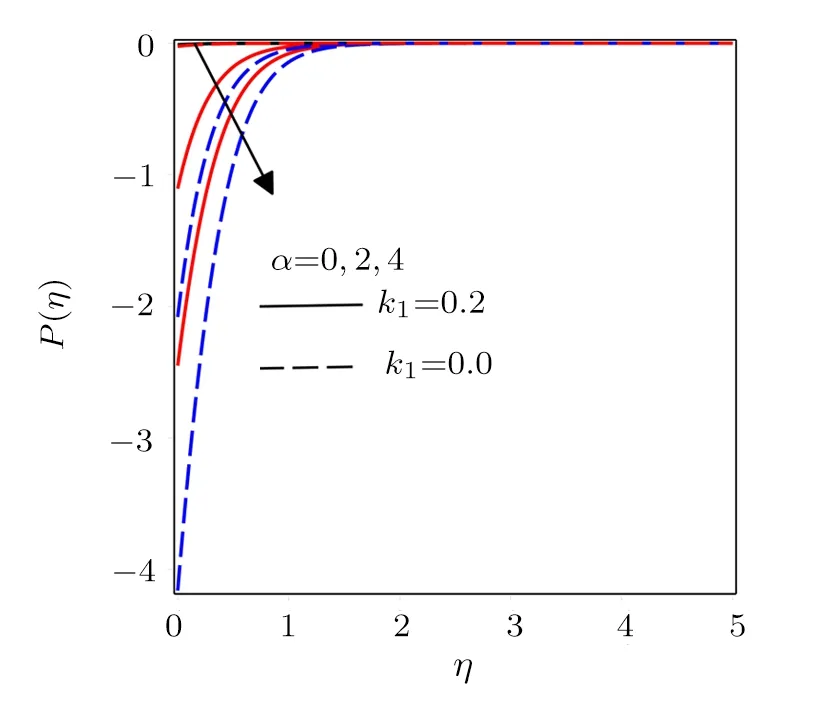
Fig.11 Influence of various values of α on P(η)with k1=0.2 and k1=0.
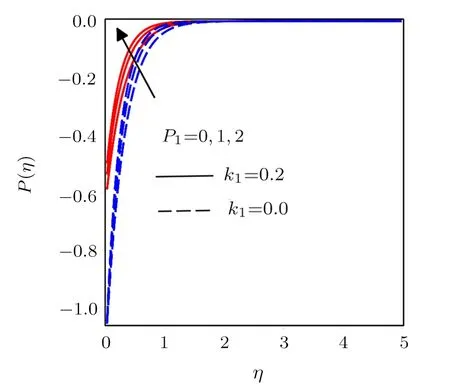
Fig.12 Influence of various values of p1 on P(η)with k1=0.2 and k1=0.

Fig.13 Influence of various values of M on P(η)with k1=0.2 and k1=0.
5 Conclusions
Darcy-Forchheimer flow of hydromagnetic viscous fluid passed through a curved stretching is analyzed in the presence of heat and mass transfer.Radiation and viscous dissipation terms are incorporated in the energy equation.RKF45 method is implemented to obtain the solution of the resultant system of non-linear equations.The results are discussed through graphs and tables of the emerging dimensionless parameters.Subsequent conclusions can be made for the present numerical analysis: (i)Velocity profiles rise due to the variations in radius of curvature and local inertia co-efficient parameter while a fall in such profiles is seen for different values of porosity and magnetic parameters.(ii)Variations in Prandtl number and radiation parameter have opposite influence on temperature profiles.(iii)Enhanced values of Schmidt number declined the concentration profiles.(iv)Pressure profiles decay for larger values of inertia co-efficient parameter and radius of curvature while the profiles climb for rising values of porosity and magnetic parameters.(v)Increased values of radiation parameter amplify heat transfer rate.(vi)Heat transfer rate reduce in case of PST and enlarge for PHT by varying Eckert number.
 Communications in Theoretical Physics2019年3期
Communications in Theoretical Physics2019年3期
- Communications in Theoretical Physics的其它文章
- Entropy Quantization of Schwarzschild Black Hole
- Pull-in Instability Analysis of Nanoelectromechanical Rectangular Plates Including the Intermolecular, Hydrostatic, and Thermal Actuations Using an Analytical Solution Methodology
- Boundary Layer Flow over a Curved Surface Imbedded in Porous Medium
- Spin-Dependent Electron Tunneling in ZnSe/Zn1−xMnxSe Heterostructures with Double δ-Potentials
- Interaction of Wave Trains with Defects∗
- Modulated Dust-Acoustic Wave Packets in an Opposite Polarity Dusty Plasma System
