基于eMBB、mMTC、uRLLC场景的第五代移动通信方法研究

陈虹旭 李菲 李晓坤 邵娜 郑永亮 杨磊

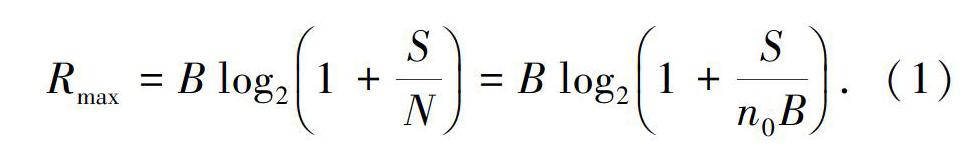
摘要：由于极化码在5G标准化中起到的重要作用，本文基于第五代移动通信在三大场景的关键技术方法，研究了系统极化码在联合信源信道编码中的使用，并通过网络传输，对数据压缩量进行研究。结果表明，系统极化码可以实现分布式压缩，其速率接近理论界限，对于较弱的压缩和较长的块长度可以降低误码率，同时对于更强的压缩和更短的块长度，可以更好地减小传输中发生的错误。

关键词：第五代移动通信：eMBB：uRLLC;mMTC;系统极化码

0引言

随着通讯需求的日益增长与全球移动通讯技术发展的日新月异，第四代移动通信已无法满足人们在工作生活中对于移动网络通讯的需要。工信部2018年11月底信息记录，现如今4G用户达11.5亿，宽带用户总数达4.05亿。用户数量的增长导致第四代通讯网络极高负荷，第五代移动通讯应运而生。1TU针对第五代移动通讯定义了三大应用场景：eMBB（enhanced Mobile Broadband）场景、mMTC（Massive Machine Type Communications）场景和uRLLC（Ultra Reliaue Low Latency Communications）场景。本文基于三大场景的第五代移动通信技术，进行其传输信道，即高斯信道建模，将高斯信道建模构造成实际现实系统的简化方案。其中JSCC信源信道联合编码系统基于系统极化码设计，满足第五代移动通信（5G）的最新技术。本研究可以投射到网络环境中，其中无线传感器网络将观测数据传输到中心节点进行解码。经过仿真环境设置，研究结果表明，系统极化码可以实现分布式压缩，其速率接近理论界限，对于较弱的压缩和较长的块长度可以获得更低的误码率，更强的压缩和更短的块长度可以更好抵抗传输错误。

1第五代移动通信标准

1.1eMBB场景

关于增强的移动宽带（eMBB），场景的业务指标，在3GPP的技术文件TR22.891和TR38.913中给出了相应的描述。eMBB旨在显著改善移动宽带接人的数据速率、延迟、用户密度、容量和覆盖范围。有助于满足对更快传输数据速度和不断增长的移动数据量的需求。随着科技的不断发展，應用对于宽带的要求只会越来越大，也必定会超过当前应用对宽带的需求。而eMBB将有助于车辆与车辆千兆位连接，数据密集型等较新应用的实现。即使在智能高速公路等较为拥挤的环境中，也能够实现AR/VR应用的实时数据流传输。这些应用的实现提升了用户体验性能，eMBB场景的目标是人与人之间极致的通信体验。考虑到人们对于经济方式的要求，5G网络也必须用更低的每比特成本传递数据。

1.2mMTC场景

海量机器类型通信（mMTC），又称大规模物联网，是指跨越大量设备的服务。mMTC实现了设备装置或技术在数量上尽可能多的参与到物联网中，满足人们对于覆盖区域，连接支持，功耗成本，网络带宽等一系列因素的需求，保证大量相邻设备同时享受顺畅的通信连接。例如，传感器这种设备，尽管每个传感器产生的数据量通常非常小，对移动通信网络的总体流量所具有的影响也非常微弱。可一旦部署数百万甚至数十亿个传感器，就会产生重大影响。就技术要求而言，mMTC并没有过高的要求非常低的延迟。虽然制动器的成本同样有限，但其可能具有不同的能量，范围从非常低到中等的能量消耗。然而，连接设备的绝对数量严重挑战了网络提供信令和连接管理的能力。为了解决这个问题，同时满足不损害设备所需的安全功能。移动网络可通过短程无线电接人技术提供设备连接，例如Wi-Fi、蓝牙、6LoWPAN等。连接设备后，移动网络经由网关提供超出本地区域的无线连接，从而实现尽可能多处理不同的应用。mMTC与现有网络共存，更加侧重人与物之间的信息交互。具有广覆盖、多连接、大速率、低成本、低功耗、优架构等特点。使得许多设备支持嵌入式高速传感器、停车传感器和智能电表等应用。

1.3uRLLC场景

超可靠和低延迟通信（uRLLC）将有助于支持关键任务应用程序，使用户和设备能够以最低延迟与其它设备进行双向通信，同时保证高网络可用性。与当前移动通信系统相比，一些设想的5G用例，例如交通安全、关键基础设施、行业过程的控制，可能需要更低的延迟。虽然传输到设备和从设备传输的数据的平均量不大，但是更大的瞬时带宽将有助于满足对于容量和延迟要求。由于应用程序级框架的要求和媒体编解码器限制可能会导致实际应用中更高的延迟，而为了支持这种对延迟至关重要的应用程序，5G允许应用程序端到端延迟1毫秒。uRLLC主要体现物与物之间的通信需求。因许多服务将在靠近空中接口的地方分配计算容量和存储，这将为实时通信创造新功能，并将在娱乐、自动驾驶车辆、工业过程控制等各种场景中实现超高的服务可靠性。

2三大场景关键技术

2.1编码技术

2.1.1极化码基础

极化码是由Arikan教授在2008ISlT国际信息大会上提出，是目前唯一一种可以证明达到信道容量极限的信道编码方法。分为系统极化码与非系统极化码，是一种新的高效编码技术。具体实现过程为N个信道组合和分离，获得相关性，当N接近无穷大时，子信道发生信道极化，一部分的信道容量趋近于1并且另一个子信道的容量趋近于0。

针对极化码编码结构的解码方案，Arikan提出了连续消除（SC）解码算法，另一种就是置信传播方法，但二者相比，前者拥有较低的复杂度，

本文将应用系统极化码以及系统极性译码器算法进行模拟仿真。

2.1.2香农极限

极化码与Turbo码、LDPC码相比，具有更好的性能和更低的复杂度，与香农极限相近。

Claude Elwood Shannon于1948年首次提出香农定理，该定理是在信号处理等领域的研究中，计算信号在白噪声干扰信道中，经过一段距离，信号衰减后得出的公式：

其中，Rmax为最大传输速率bit/s;B为频谱宽带;S为信号功率（W）;V為信息速率（bit/s）;n₀为噪声功率谱密度;N为噪声功率（W）;S/N为信噪比（dB）。

香农定理表明，如果V≤Rmax.则理论上存在一种方法使得信息以一种任意小的错误概率通过该信道。

如果信息速率V>Rmax.理论上信息无法通过该信道，或者此信息以50%错误概率通过该信道。

由香农公式可得出信噪比与信道带宽的关系，以及信道宽带对传输速度的限制。由于现代宽带无线制式不同，导致信道容量极限不同，而信道容量也不仅取决于信息信噪比，还取决于编码技术。基于香农定理，极化码编码技术可在通信领域中实现高效、可靠的大信道容量通信传输。

2.2非正交多址技术

非正交多址技术（NOMA）为第五代移动通信三大场景中至关重要的传输技术。在发送端，采用非正交传输并主动引入干扰信息：在接收端，通过串行干扰删除实现正确调节。与传统的正交多址接入相比，无线电允许多用户在同一时间，同一频率传输信号和接收信号，非正交多址技术可以提高频谱利用效率，扩大吞吐量，具有低延迟，高可靠性，同时也可以支持更大规模的设备与其进行连接。因此，非正交多址接入技术成为第五代移动通信的核心技术之一。

NOMA的2种主要类型是：电源域和代码域。电源域NOMA的关键特性是允许不同的用户共享相同的时间、频率和代码，但具有不同的功率级别。在代码域NOMA中，将不同的扩频码分配给不同的用户，然后在相同的时频资源上复用。另外，在功率域NOMA中，现如今主要采用串行干扰删除技术来大幅的减少多址的干扰等问题。

串行干扰消除技术的主要思想是逐步消除干扰。在接收信息一端采用具有串行干扰消除技术的接收机来消除干扰。接收信号中对用户逐一进行解码，完全解码后，在接收信号中减去这个用户信号带来的多址干扰，然后对其余用户根据一定顺序再次进行循环解码，循环多次消除同一时刻同一频率所有的多址干扰。NOMA基本模型如图1所示。

2.3D2D

D2D终端直通技术是第五代移动通信中三大场景的重要技术，支持不占用频谱资源的直接通信。在本文仿真实验中，应用D2D技术通过复用通信网络资源，实现终端与终端之间交换信息。从蜂窝网络覆盖范围来看，D2D通信可分为基于蜂窝网覆盖下的D2D连接和无蜂窝网覆盖下的D2D连接。基于蜂窝网覆盖下的D2D连接又可分为全部覆盖与部分覆盖。当全部覆盖时，首先通过基站搜索D2D设备，然后进行连接，在成功进行资源的管理、调度、分配等一系列操作后，实现用户之间通讯。当部分覆盖时，因其网络复杂度远低于全覆盖下的D2D连接，无需进行资源调度即可通过基站成功引导D2D设备连接，实现用户之间通过D2D技术的通讯。无蜂窝网覆盖连接时，用户与用户可直接通讯。

根据随机几何理论，BS基站空间分布可利用泊松点分布建立强度为h8s的网络模型。

其中，ψ（A）为计数测度，|A|为勒贝格测度。将用户建模分为两组，一组为D2D传输Ue.建立强度为λ_tx，的泊松点分布模型，另一组为D2D接收Ue.建立强度为λ_rx的泊松点分布模型。其中UE为用户设备。

假定D2D模型的选择基于蜂窝网连接和D2D连接的下行信号强度DL。因下行信号通过UE的测量结果可经首层与末层进行平均，所以只考虑下载信号强度路径损耗即可，通常根据幂法则，可得下行信号强度。

其中，x为传输信号位置;y为接收信号位置;i为蜂窝网连接与D2D连接;|x-y|为输入信号与输出信号之间的距离;P_I为传输能量效率;G_I为天线增益;ηi为信号传播路径损耗;A_i为信号传播常数。

移动模型代表移动用户的移动，可以用来预测用户的未来位置。在一个新的移动adhoc网络协议的研究中，模拟协议及评价其性能非常重要，移动模型是协议模拟的关键参数之一。随机路点移动模型为移动模型的一种，其用户轨迹可用其无限的四重序列表示：

其中，X_n-1为初步位置;X_n为结束位置;V_n为速度;S_n为到达航点暂停时间。给定当前的航点X_n-1，得出一个密度为λ₁同质泊松点分布ψ_i（n），选择距离ψ₁（n）最近的点作为下一个航点。

由此可知，变化长度呈瑞利分布。

D2D模型的选择基于蜂窝网连接和D2D连接下行信号的强度DL。一般来说，2种选择之间无明确界限，本文中给出一种方式，当用户超出D2D范围时，给出模式选择界限，其中D2D以用户设备为中心，通信范围由等待偏置的DL的边界来界定。对于传统的D2D传输Ue.边界由BS和D2D传输UE的相同DL边界平面点来界定。

其中，γ_c和γ_d为蜂窝网连接和D2D连接的数据流量减负偏差，根据D2D传输UE时选择模式的多种情况，D2D接收UE将选择最先接触DL边界的用户设备，

一般情况下假定BSl_BS位于起点，由D2D传输UE位于x_t（d.0），由D2D接收UE位于（x.y）∈r.其中，D2D接收UE到BSl_BS的距离为：

当D2D模式转换速率提高时，传输UE通信模式的频率也将提高，这直接有助于系统指令开销。对于传输UE运行轨迹L^′，可将强度为λ_t的随机路点移动模型分为无限个移动小区间。因此，D2D模式转换是在一个移动区间内的转换。

其中，E_N为预期数量，E_T预期时段时间。对于传输Ue.在第n个移动区间执行D2D模式转换的概率可表示为接收UE位于areal和area2的概率，即：

求整个概率空间上的平均值，计算出传输UE的预期D2D模式转换数：

为了得到DL边界圆半径的概率密度函数，需得出BS输出UE与D2D输出UE之间的距离d的概率密度函数X_t2b。X_t2b>r事件等同于以半径为r输出UE的圆内没有部署BS的事件，因此，X_t2b>r的概率为：

平均变化时间可以通过使用预期变化长度和平均速度的比来求导出，即：

2.4系统极性译码器算法

本文设计了一种高效、低复杂度的算法来执行系统的极坐标编码，适用于任意选择的冻结位索引（不一定是极坐标）。其具体过程如下：

功能编码器A（y.x）

INPUT：y.x with unfilled bits（variables of x=可得：

系統极性码中消息向量被映射到码字，使得消息比特显示可见。考虑码字X中消息位的索引显示，可以选择与信息位索引i的集合相等的集合。在该集合中，消息位显示为第k位。

其中，x和y是未知数且二者之间有N个未知量，很容易看出得到的x是一个重新排列的线性方程组。且F^×n是一个上三角矩阵，可以直接用高斯消去法求解方程。

2.5实验系统模型

基于三大场景第五代移动通信关键技术的无线传感器网络背景，将常规的信息源数据传输到中央基站进行解码，如图2所示。传感器1使用系统极性编码器独立编码得其数据X。在系统极性编码器的输出端，当通过噪声信道时，将系统位d.丢弃，将奇偶校验位d_p发送到基站。当奇偶校验位的数量不超过系统位数时，则进行压缩。传感器2采用信源编码与信道编码技术来传输其观察到的信号数据y.在基站处具有相应的常规解码器。在接收端，系统极性译码器使用解码后的数据Y（近似为Y）作为解码X所需的系统数据的噪声。

利用传统编码技术，Y可以被压缩到接近其极限熵H（Y）的速率并且可被解码器正确恢复Y′=r.使用任何合适的熵编码方案都可以实现向前纠错码。如前所述，通过在解码器处利用X和Y之间的相关性，可将J的速率压缩接近条件H（X/Y），因H（X）≥H（X/Y），所以与H（X）相比，采用Y来解码x.不能够实现最大强度压缩。对于i（n.K）系统极性编码器，当N<2K时实现压缩，并且Z的压缩率为：

根据离散无记忆信源z.‘0与‘1符号可能性相等的情况。为了模拟数据之间的相关性，使用虚拟通道在其输入处得到x.并在其输出处得到Y。由于Y不一定是离散的，因此考虑到高斯相关模型，可以简化系统模型，如图3所示。

其中关联模型被模拟为高斯模型。二进制数据X被反馈到二进制脉冲幅度调制器（B-PAM），其输出矩形脉冲幅度为±E_b^1/2，持续时间为T_b，然后添加高斯随机变量（RV），对信道输出进行采样以获得数据Y。该信道关联模型借鉴于通信理论，其中E_b表示比特能量，加性高斯RV表示功率谱密度为N₀/2的零均值加性高斯白噪声（AWGN）。X和Y之间的相关性可以通过比特能量与噪声密度比E_b/N₀来测量，比率越高，相关程度越大。根据Slepian-Wolf定理，只的下限是H（X/Y），压缩界限可表示为：

公式中E_b是平均比特能量。通常情况下一个Bit是由很多个chip组成的，所以其能量=N*E_c。No是Noise的缩写，指白噪声的功率谱密度，其单位是W/Hz。

E_c/N_o定义为：每个调制比特的能量与噪声功率之比。RSSI接收信号强度指示（接受信号功率/整个信道带宽内的接收功率），相应信道带宽内的宽带接收功率，测量在UTRAN下行载波上进行。

实际上，可实现的速率（取决于代码设计）与理论界限之间始终存在差距。在JSCC系统模型下，需要额外的冗余位来克服信道损耗，因此与H（X/Y）之间的差距进一步增加。

本研究中，对于（N，K）码，选择输出第N个比特位（系统位加上奇偶校验位）为2的幂（N=2ⁿ，n=8.10.12.14.16.18）。而对于给定的N值，通过改变输入数据位的数量及来改变压缩率。

在系统极性编码器中，输出码由系统位和奇偶校验位组成，使得：

其中，系统位部分是d_s=d_{i}=x_{i}，奇偶校验位部分是d_p=d_{i}c。系统极性编码器中的系统位不是输出码字中的前K个位，类似于系统线性分组编码，但它们出现在系统极性编码器输出的信息位索引处，因此，奇偶校验位被置于d中的冻结位索引处。给定信息向量x.系统极性编码器的输出码d为：

3实验结果与分析

本文研究了在三大场景中第五代移动通信关键技术的无线传感器网络背景下，系统极化码在联合信源信道编码中的应用。使用高斯模型来表示源相关，采用高斯信道进行传输。模拟了两个简单场景。研究表明，利用较弱的压缩和较长的块可以降低错误率，然而更强的压缩和更短的块长度可以更好的降低传输错误。

在模拟中，首先考虑DSC分析法的情况，其中没有噪声作用于奇偶校验位。差距在可达到的压缩率与理论压缩界限之间，目标误码率（BER）在1E-6时，使用不同n∈{8.10.12.14.16.18}值的系统极性译码器，得到结果如图4所示。

由图4可以观察到：随着X和Y之间的相关性E_b/N₀的增加，H（X/Y）减小。这些曲线表明，对于所需的压缩比，当n减小时，需要更大的能量与相关噪声比，以实现所需的误码率性能。

在图5中，以0.6的压缩率获得的不同n值的误码率，绘制了不同系统极性编码器获得的误码率（BER）作为条件熵的函数。对于这种压缩率，n=18所显示的误码率最低，因此n=18在这种情况下的压缩率表现最佳。

在图6中，H（X|Y）固定为0.085.并且针对不同的压缩率测量误码率。已知，無论n为何值，更强的压缩都会导致误码率的增加。通过观察较大n值（n=14.16.18）的数据情况，可以注意到，当压缩率<0.4时，误码率随n增加而增加。在压缩率>0.4情况下，误码率随n值的增加而急剧下降并减小。这是因为在具有非常大的N的（N，K）系统极性编码器中压缩率接近零时不能实现低的误码率，这与在信道编码应用中使用的极化码的情况不同。可通过增加N来获得更好的性能，但其最大值受物理条件约束，

在评估了DSC系统之后，接下来研究了JSCC系统的情况，即传输信道误差对系统性能的影响。如在JSCC场景描述中所提到的，假设Y在解码器处成功恢复（使用传统的源和信道编码技术），而SPE共同用于压缩和前向纠错，用于源X的传输和重建。相关信道与DSC相同，而符号能量与噪声密度比E_b/N_o在传输信道（即奇偶校验位的信道）上变化，以便在误码率方面分析JSCC系统性能。考虑压缩率为0.45和0.64时误码率的情况。如图5所示，由于传输源的不确定性由噪声的传输而增加，造成H（X/Y）的差异。因此，本文中将误码率曲线绘制为相关参数E_b/N_o的函数。

通过分析图7到图lO可以得出2个主要结论。

（1）针对于较弱的压缩和较长的块长度，可以获得更低的误码率见表1。

通过比较可得结论，在相同压缩率时，较长的块长（n=16）度拥有更低的误码率见表2。

通过比较可得结论，在相同块长度时，较弱的压缩（压缩率=0.64时）拥有更低的误码率。

（2）更强的压缩和更短的块长度可以更好抵抗传输错误。例如，计算E_c/N_o在同一E_b/N_o下的平均误码率，块长度从n=12增加到n=16.压缩比为0.45时，块长度误码率从1245倍增加到21087倍，增加约16.93倍。当压缩比为0.64时，误码率从134.4倍增加到2330倍，增加约17.33倍。则可得出结论，在0.45.n=12时，误码率增加倍数更少，系统抗噪声能力越强，能够更好地抵抗传输错误。

4结束语

本文研究了在基于三大场景的第五代移动通信关键技术的无线传感器网络背景下，系统极化码在联合信源信道编码中的应用。利用高斯模型来表示源相关，采用高斯信道进行传输，模拟了2个相关源的简单场景。研究表明，利用较弱的压缩和较长的块长度可以降低错误率，更强的压缩和更短的块长度允许更好抵抗传输错误。本文结合第五代移动技术三大场景，对三大场景的关键技术分别进行了解析，证明了通过应用系统极化码仿真得到的通信性能更好、可靠性更强，更符合现如今信息技术的发展需要。