弯曲河流颈口裁弯不同阶段水流运动特性

吴新宇,李志威,2,胡旭跃,2,陈 帮,杨 玥

(1.长沙理工大学水利工程学院,湖南 长沙 410114; 2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114)

自然裁弯是弯曲河道演变由渐变发展到一定阶段后出现的突变现象,是河流内在的自组织调节机制。弯曲河流在演变过程中弯曲度逐渐增加,达到临界值后会因洪水过程或崩岸贯穿发生裁弯,降低弯曲度,促使河道启动新一轮的横向演变[1-3]。裁弯是弯曲河流演变过程中的突变事件,也是牛轭湖形成的最主要方式。裁弯的研究在世界各地的弯曲河流中均有较多报道,比如我国长江中游荆江、渭河下游和塔里木河中下游[2-4],密西西比河下游[5]、Wabash河[6]和Powder河[7],英国的Bollin河[8]和澳大利亚的Hunter河[9]等。颈口裁弯是河湾的颈口不断缩窄,洪水作用使得上、下游河道交汇形成新的河道,旧河道逐渐淤积形成牛轭湖。颈口裁弯通常出现在洪水期高水位条件下,需要多次高水位漫滩水流冲刷才能实现[7],崩岸贯穿的裁弯模式在滨河植被发育良好、河岸物质组成为二元结构的弯曲河流较常见[1]。

以往关于颈口裁弯的研究多数是基于野外观测开展。潘庆燊等[4]对长江中游中洲子和上车湾两处裁弯工程的原型观测表明,裁弯发生后,新、老河道的水流和泥沙条件均发生改变,新河经历普遍冲刷、弯道形成和弯道正常演变三个阶段,横断面变化过程是先变深后变宽。老河淤积经历河道型淤积、单向淤积和牛轭湖形成三个阶段。裁弯对上游河道影响较大,使上游比降增大,水位降低,对下游河道基本没有影响。前人的野外观测表明颈口裁弯通常历时短暂,短时间内完成新河槽形成过程[10-12]。尽管野外观测是重要的研究手段,但是不能长时间连续观测水流结构的变化和河道冲淤的过程,已有的野外观测均没有涉及裁弯过程中的水动力测量。

目前,已有许多学者研究弯道水流的数值模拟[13-14],然而关于颈口裁弯水动力数值模拟的研究成果很少。早期,谢鉴衡[15]以在适当的假设条件下计算人工裁弯实施前后河道分流情况和河床变形情况，设计引河断面,但不涉及具体的流场分布情况。Fares[16]在野外观测数据的基础上建立二维规则弯道水流数学模型,重点研究颈口裁弯交汇区流速和边界剪应力。最新研究也有利用三维数学模型研究裁弯对上下游河道的影响[17],但是没有涉及裁弯过程中新、老河道的逐步发展过程。裁弯过程中新、老河道的水动力变化过程的数值模拟研究尚未见报道。由于颈口裁弯过程的短暂性和实际野外观测的局限性,建立三维水动力学数学模型模拟颈口裁弯过程具有较高的科学参考价值。

本文以黄河源若尔盖的泥炭型弯曲河流两处裁弯的野外观测颈口裁弯资料为基础,建立基于不可压缩雷诺平均Navier-Stokes方程、k-ε紊流模型和有限体积法的MIKE 3 Flow Model水动力模型,分析颈口裁弯形成过程中不同阶段的流场变化,以期有助于深入了解裁弯的水动力过程,进而为预测颈口裁弯的泥沙冲淤过程提供有价值的参考。

1 数学模型及验证

1.1 基本方程

MIKE 3 Flow Model是通用三维数学模型,可用于不同类型水体的三维非恒定流模拟[18]。主要假设有Bousinesq涡黏假定和静水压假设。水动力控制方程是不可压缩雷诺平均Navier-Stokes方程[19]

采用σ坐标，垂向网格σ坐标变换公式为

(1)

式中:z为笛卡尔坐标中的垂向坐标;d为静水深;η为自由水面相对于基准水面的高程。

连续方程与动量方程为

(2)

(3)

(4)

式中:t为时间;x、y、z为笛卡尔坐标;u、v、w分别为x、y、z方向的速度;h为总水深,h=η+d;f为柯氏力系数;g为重力加速度;pa为空气大气压力;ρ为水的密度;ρ0为水的参考密度;Sxx、Sxy、Syx和Syy为分散应力张量的分量;Fu、Fv为水平应力量;vt为垂直方向的涡黏系数;us、vs为源(汇)流向外界的流速分量;S为源(汇)流量。

k-ε紊流模型闭合方程为

(5)

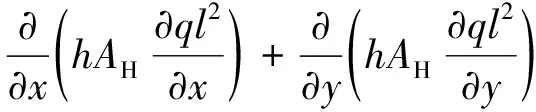
(6)

式中:q2为2倍紊动动能;l为混掺长度;Aq、AV分别为垂向和水平扩散系数;Ab、AH分别为垂向和水平紊动扩散系数；B1、E1、E3为经验参数。

(7)

式中:L-1=(η-z0)-1+(h-z0)-1,其中z0为河底高程;E2为经验常数,取1.33。

1.2 数值求解方法

MIKE 3将计算区域在垂直方向上分为若干层求解,首先确定每层内二维变量,再结合连续方程求得垂直方向的分量。方程的求解采用显隐式交替技术,浅水方程的时间积分和输移(扩散)方程基于半隐格式求解,相应平流项采用显式格式求解,而垂直对流项则采用全隐格式求解。时间步长要求严格满足CFL数小于0.8。

1.3 模型验证

采用Abhari等[20]的90°弯道模型进行验证。弯道总长11.3 m,宽0.6 m,上游直段长5.5 m,下游直段长2.8 m,弯曲段内外半径分别为1.5 m和2.1 m(图1)。上游进口流量为0.03 m3/s,下游出口水位为0.20 m。水平方向划分1 064个网格,640个节点。垂直方向划分30层。河床粗糙高度0.005 m,采用高阶计算模式,时间步长0.001 s。选取30°、60°和90° 3个过水断面,纵向流速的垂向分布计算值和实测值的对比见图2,横向流速的垂向分布计算值和实测值对比见图3,计算值和实测值非常接近,模型精度较高。凹岸与凸岸水位差的成果见表1,两岸水位差值小于2 mm。由于文献[20]中未见水位的测量数据,在此仅对流速分布进行验证。

图1 验证模型平面(单位:m)

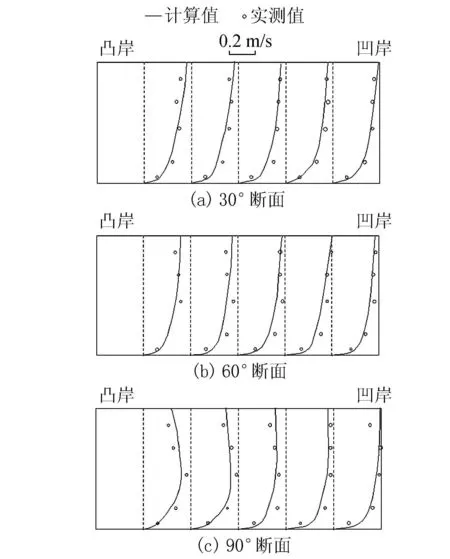
图2 纵向流速垂向分布的计算值与实测值对比

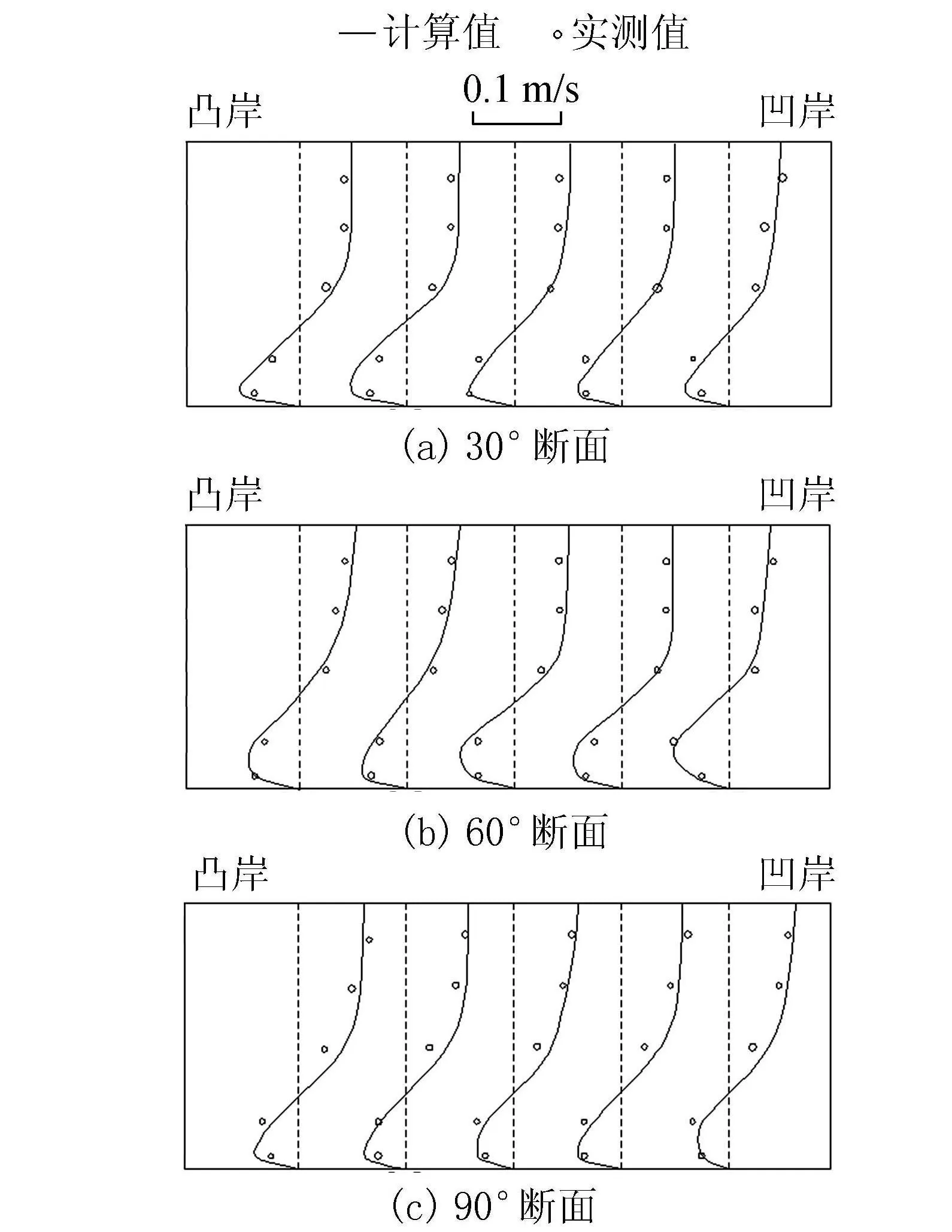
图3 横向流速值的垂向分布计算值与实测值对比

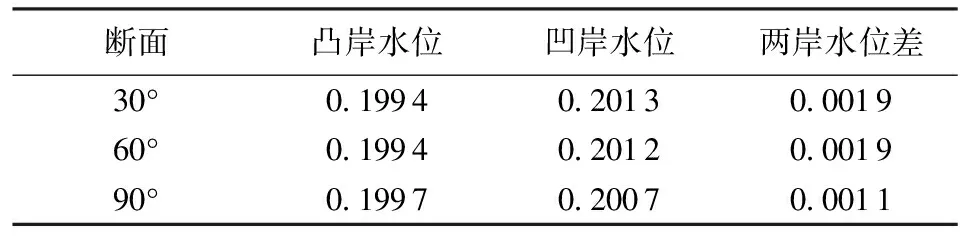
表1 计算得到的两岸水位 m

2 裁弯水动力模型建立

基于2013年、2014年和2016年7月对黄河源若尔盖的泥炭型弯曲河流(黑河支流,哈曲上游)的实测资料建立数值模型,研究区域为两处裁弯的弯道及其上、下游(图4)。裁弯1(NC-1)位于北纬103°03′14″,东经32°56′55″,计算河段长300 m。裁弯2(NC-2)位于北纬103°03′07″,东经32°56′47″,计算河段长405 m。河岸物质组成具有明显的二元结构,上层为泥炭层,下层为湖相的粉沙,夹杂河流相的粗沙或卵石。

图4 黄河源若尔盖黑河上游的2个裁弯位置(2016年7月)

数值模型共计8种工况(表2),包括2013年未裁弯，2013年开始裁弯,2014年、2016年裁弯情况。模型进、出口均控制流量恒定,依据实测资料,进、出口流量均取Q=3.0 m3/s,河床粗糙高度取0.005 m,采用高阶计算模式,时间步长取0.001 s。

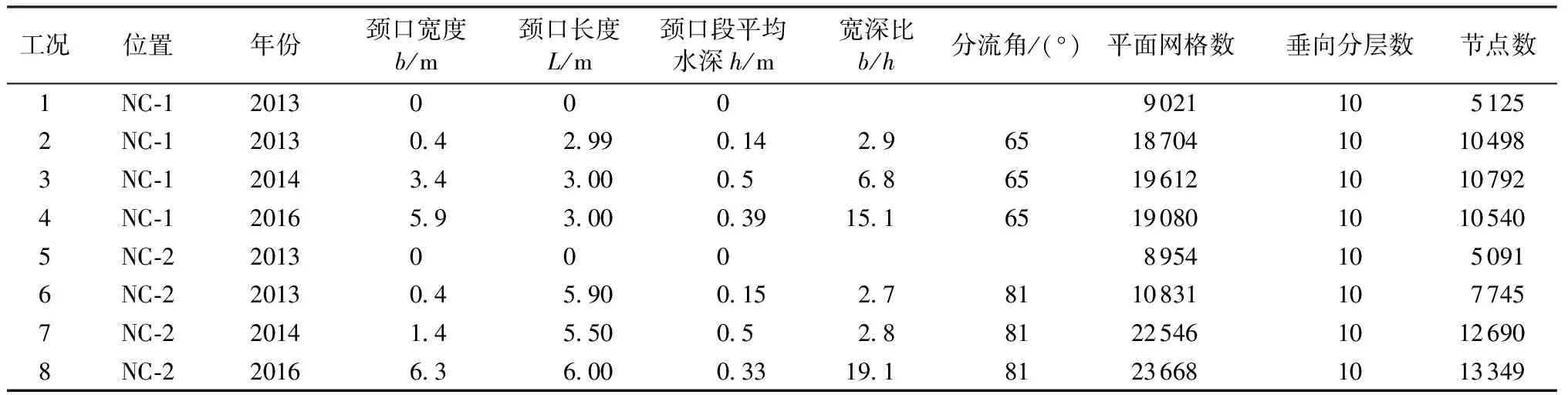
表2 数值模拟工况

对于各工况下的地形数据作以下处理。

裁弯1:2013年河道原始地形(工况1)坡降取0.36%(实测值),河宽3.7～5.8 m,横断面简化为矩形。2013年开始裁弯时(工况2),人工裁弯颈口段水深0.16 m,颈口宽度为0.4 m，颈口段坡降为0,原河道地形仍然为未裁弯时的地形。裁弯发展到2014年(工况3),根据实测数据,颈口宽度已经展宽为3.4 m,颈口处被水流冲刷下切,水深已经达到0.5 m以上。老河道进口左侧冲刷严重,出现崩塌现象;而右侧则淤积严重,右侧水深只有0.20 m。由于2014年实测资料较详细,新、老河道的地形均采用实测资料。2016年(工况4),颈口宽度已经展宽为5.9 m;与2014年相比,颈口处有泥沙淤积,水深为0.45 m。老河道进口基本被淤死,高水位时有水流流过,低水位时无水流通过。颈口段地形采用实测数据,将老河道进口断面形态和2014年对比,认为2016年老河道的地形在2014年的基础上淤高了0.05 m。

裁弯2:2013年河道原始地形(工况5)坡降取0.36%(实测值),横断面简化为矩形,河宽2.7～7.0 m。2013年开始裁弯时(工况6),人工裁弯颈口段水深0.15 m,颈口宽度为0.4 m;颈口段坡降为0,老河道地形仍然是未裁弯时的地形。2014年(工况7)人工裁弯颈口段宽度为1.4 m,水深为0.5 m,颈口段横断面简化为矩形,老河道进口断面用实测资料,其他地方横断面仍然简化为矩形,参考裁弯1中2014年地形的变化,认为2014年裁弯2处老河道的地形在2013年基础上淤高0.30 m。2016年(工况8)颈口段新河道宽度达到6.3 m,新河道地形采用实测数据,坡降为0。2016年老河道的地形在2014年的基础上整体淤高0.15 m。

本文所涉及的河道断面位置见图5。

图5 裁弯1断面位置

3 结果分析

3.1 颈口分流

裁弯发生后,一部分水流通过新河道。定义分流比为新河道的流量占干流总流量的百分比,以反映新、老河道流量分配情况[21-22]。研究分流比与新河道宽深比之间的关系,除了流量Q=3.0 m3/s工况以外,另增加两处裁弯2014和2016年Q分别为2.0 m3/s、2.5 m3/s、3.5 m3/s、4.0 m3/s和5.0 m3/s的情况。裁弯发展过程中老河道进口断面逐渐淤积,水流不断冲刷新河道,新河道横断面逐渐变深变宽。用回归分析研究新河道宽深比和分流比、过水面积之间的关系见图6。裁弯发展过程中,新河道分流比随宽深比的增大而增大,二者之间呈线性正相关关系,两处裁弯相关系数均大于0.893。分流比与过水断面面积之间的相关性并不明显。

图6 分流比和宽深比、过水面积之间的关系

3.2 河道平均流速和水深

3.2.1 平面流场变化

以裁弯1为例分析流场变化过程。裁弯1处各种工况的流速等值线分布见图7。与裁弯前工况相比(图7(a)),2013年开始裁弯时老河道的流场分布基本没有改变(图7(b)),颈口段进口处水流顶冲右岸(图8(a))。2014年人工裁弯已经历时1 a,河道主流改变方向,大部分水流沿新河道,老河道只有少量水流通过(图7(c)),颈口段新河道主流偏向右岸(图8(b))。由于只有少量水流通过,老河道流速明显减小。老河道L1断面处右岸(凸岸)淤积,左岸(凹岸)冲刷,故主流偏向左岸。2016年裁弯已历时3 a,流速分布见图7(d)。与2014年相比,颈口段主流方向基本没有改变(图8(c)),仍然偏向右岸,但流速值有所减小。老河道的流量和流速进一步减小,L1断面处主流仍然偏向左岸。

图7 裁弯1发展过程中河道流速分布的变化

图8 裁弯1颈口段进口处流场

3.2.2 平均流速和水位沿程变化

裁弯发生后,新、老河道平均流速和水位均发生改变。以裁弯1为例,分析裁弯过程中新、老河道平均流速和水位的变化情况。不同工况下裁弯1处老河道和新河道的沿程流速和水位分布见图9和图10,图9(a)、图10(a)中横坐标0点表示L1断面,图9(b)、图10(b)中横坐标0点表示N1断面。

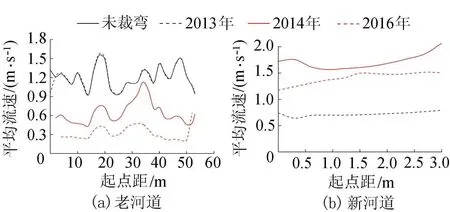
图9 裁弯1平均流速沿程分布

图10 裁弯1水位沿程分布

2013年裁弯初始(图9(a)),老河道L1断面平均流速值减小,其他区域平均流速和未裁弯时相同。2014—2016年,老河道断面平均流速逐渐减小。2013—2016年,颈口段新河道断面平均流速则是先增大后减小(图9(b))。裁弯1处老河道水位沿程变化见图10(a)。2013年裁弯刚发生时,老河道水位基本没有变化。裁弯发展到2014年,水位升高,水面比降增大。2016年,老河道上游水位降低,下游水位有所增加,比降进一步增大。裁弯后,新河道水位的变化见图10(b)。裁弯发展到2014年,新河道水位下降,新河道比降略有增加。2016年,新河道水位和2014年相差不大。

3.3 横向环流变化

K—K断面位于裁弯1处原河道上游弯道的弯顶处,距裁弯颈口5.0 m。裁弯过程中,K—K断面垂向流场变化见图11。各阶段,K—K断面均形成横向环流,底层流速最小,表层流速最大。2013年裁弯刚发生时,K—K断面垂向流场未发生明显变化。裁弯发展到2014年,K—K断面流速值略微减小。而到了2016年,流速值又增加,恢复到未裁弯时的流场。可见,裁弯对其上游弯顶处流场的影响不是特别明显。

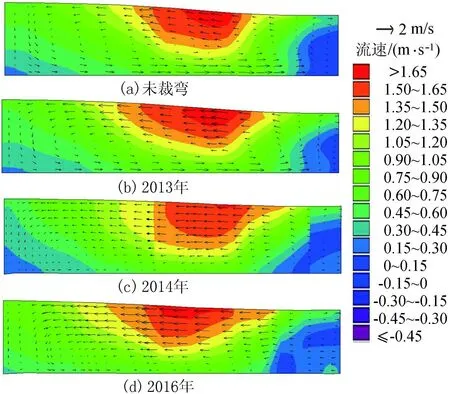
图11 裁弯1上游K—K断面垂向流场变化

裁弯1处下游H—H断面位于新、老河道交汇下游弯道的弯顶处,距裁弯颈口4.0 m。未裁弯时,H—H断面形成横向环流(图12(a)),上部由凸岸指向凹岸,下部由凹岸指向凸岸。凸岸流速大于凹岸流速,上部流速大于底部流速,符合弯道环流的一般特征。2013年裁弯初始,H—H断面流场基本没有变化(图12(b))。裁弯发展到2014年,H—H断面流场与前两种工况完全不同(图12(c))。受新、老河道汇流的影响,水流在H—H断面处形成剧烈的横向环流,环流方向与未裁弯时相反,上部由凹岸指向凸岸,下部由凸岸指向凹岸。底部流速值大于上部流速值,凸岸流速仍然大于凹岸流速。与2013年相比,凸岸流速约增加了1.0 m/s。与2014年相比,2016年H—H断面流场变化不明显(图12(d))。裁弯明显改变了邻近下游弯顶处水流结构,包括横向环流的方向和流速值的大小。

由于裁弯2处上、下游弯道距裁弯位置较远,裁弯对弯顶处水流结构影响不明显。

4 结 论

a. 黄河源若尔盖黑河上游两处颈口裁弯发生后,新河道较快冲深展宽,新河道的分流比和宽深比相应改变,而且两者呈线性正相关关系,即随着新河道的宽深比增加,分流比呈增加趋势。

b. 颈口裁弯引起新、老河道的流量发生重分配和流场重分布。裁弯初始发生时,老河道的流场基本不受影响。颈口段新河道宽深比和分流比随着裁弯发展逐渐增大,且老河道的流量、水深和断面平均流速均逐渐减小。新河道流量则逐渐增大,平均流速则呈先增大后减小的规律。裁弯后,老河道水面比降有所减小,新河道比降略有增大。

c. 颈口裁弯对上游河道流场的影响较小,但是明显改变其邻近下游弯道弯顶处流场,包括横向环流的方向和大小。