基于PSO算法的反力架设计与优化
王 凯, 张良辉, 孙振川, 李凤远, 张 兵, 王超峰
(1. 盾构及掘进技术国家重点实验室, 河南 郑州 450001;2. 中铁隧道局集团有限公司, 广东 广州 511458;3. 汕头市苏埃通道建设投资发展有限公司, 广东 汕头 515000)
0 引言
在现代机械结构或系统设计中,优化设计是一项关键技术。反力架作为盾构始发的支撑结构,伴随盾构法隧道向大直径方向发展(至2016年6月,国内直径≥14 m的盾构隧道已建成11项,在建10项)[1],其结构优化也愈加复杂,不仅要满足结构在强度、变形方面严格的要求,而且对结构的轻量化提出高要求,因此开展反力架的设计与优化研究很有必要。在盾构始发过程中,反力架为盾构提供支撑反力用来克服各类摩阻力,支撑反力达到104kN量级并随盾构直径增大而增大,重载荷下结构的强度及变形问题引起了研究人员的关注。赵宝虎等[2]在有限元计算的基础上,对长江隧道反力架开展应力监测研究,依据对监测数据的分析,选择负环拆除节点。张子辛[3]对盾构反力架结构进行应力分析,并对薄弱部位采取加固措施。李建明等[4]设计了4种轨枕路基疲劳试验机加载反力架,通过在静态强度、动态响应对比基础上优选出强度高、耗钢少的结构。诸多学者对结构优化开展研究,史国宏等[5]采用参数化车身模型,通过多学科优化过程,找到白车身零件形状、尺寸、位置与厚度等各参数之间的最佳组合,实现了结构轻量化的目标。郭京波等[6]利用遗传算法对刀盘的设计开展优化研究,降低了载荷合力及倾覆力矩。李斌斌等[7]在对土压刀盘数值分析的基础上,通过对刀盘结构尺寸进行改进优化,使该刀盘在正常工况下的强度提升,刀盘面板外边缘处的变形量减小约25%。已有研究对反力架进行结构优化时,主要在强度分析的基础上对薄弱结构加强或进行方案优选,并未建立起优化的数学描述。本文以结构件厚度为设计变量,强度及变形为约束条件,针对反力架建立起轻量化的目标优化,并采用PSO算法成功求解了反力架的优化问题。
1 反力架的结构设计及计算
1.1 反力架的结构
反力架为框架式钢结构(见图1),设计尺寸为17 m(宽)×18.5 m(高),中心部位预留环形区用于后配套设备通过。其主要由正面板、背面板及腹板组成,安装时底部支座与混凝土内预埋件连接; 左、右侧腹板及背面板与支撑系统(钢支撑)连接。盾构始发时,油缸推力产生的反作用力经管片传递作用在正面板上,经支座、支撑系统最终传至始发井混凝土结构上。反力架采用的材料为Q345,面板采用厚40 mm的板材,腹板采用厚30 mm的板材。
1.2 反力架有限元模型
1.2.1 有限元模型建立
建模过程中,简化掉对模型影响不大的局部特征,忽略螺栓孔、吊耳等。反力架由钢板焊接制造而成,在三维几何建模的基础上抽取中面,采用板壳单元(Shell)离散。对于个别区域板之间为锐边连接,网格离散后质量较差的情况,修改该部分模型。背面板区域与22根钢支撑连接,腹板与8根钢支撑连接,连接均采用节点耦合的方法处理。运用3种网格(70、50、40 mm)进行网格独立性验证,结果表明网格的种类和网格尺寸对结果影响很小,最终整个模型网格全局尺寸控制为50 mm; 对于与支撑系统连接的部位,进行局部网格细化,尺寸控制为25 mm。整个模型单元总数为760 646,节点总数为739 399。

图1 反力架结构设计图(单位: m)
1.2.2 材料参数
反力架结构的材料为Q345,其详细材料参数见表1。

表1 Q345材料参数
1.2.3 载荷及边界条件
1.2.3.1 载荷
盾构工作时受力较复杂,计算时盾构总推力按照经验公式[8]确定。
F=βD2。
(1)
式中:β为经验系数,一般取为500~1 200 kN/m2;D为盾构直径。
佛莞狮子洋隧道和苏埃通道盾构均在淤泥地层始发,盾构轴线埋深均在20 m附近,端头区都采用“旋喷加固+素墙+注浆+降水井”方案施作,不考虑地下水的影响,采用经验类比的方法对推力进行估算,依据狮子洋隧道泥水盾构(D=13.56 m)前50环掘进推力数据(见表2),对苏埃通道盾构(D=15.03 m)始发推力进行推算,结果见图2。经过推算得到苏埃通道盾构始发前50环最大推力为57 615 kN(近似为60 000 kN)。
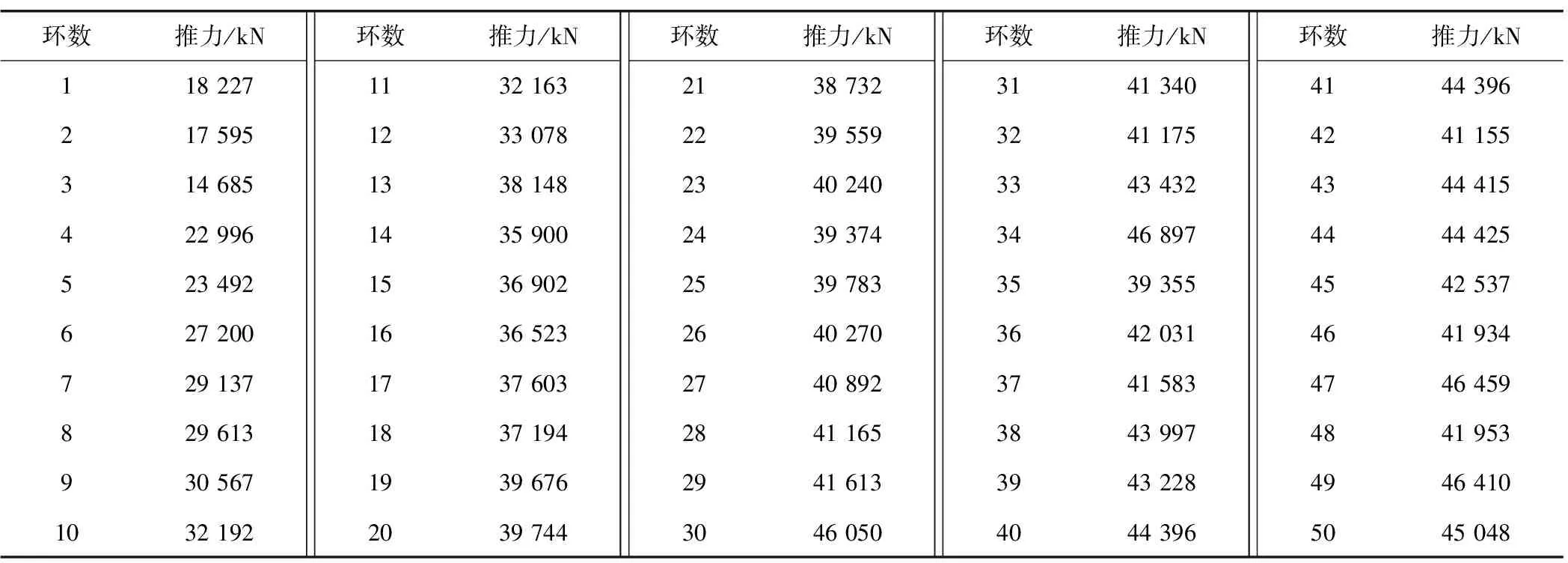
表2 狮子洋隧道前50环推力数据
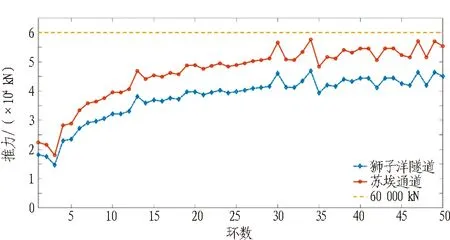
图2 苏埃通道盾构始发前50环推力预测
Fig. 2 Segment thrust forces prediction of first 50 rings of Su′ai Tunnel
1.2.3.2 边界条件
反力架底部通过6个支座结构与始发井预埋件连接,左右两侧各4根钢支撑、背面板后22根钢支撑及另外2根斜支撑均与始发井主体结构通过预埋件相连,将钢支撑端部视为固定端约束。施加载荷和边界条件后的模型见图3。

图3 施加载荷和边界条件后模型
1.3 有限元分析结果
采用静力学分析的方法计算反力架在60 000 kN载荷下的最大变形及应力分布规律。采用等效von-Mises应力作为结构的评定标准。反力架的等效应力云图见图4。从图4可见: 加载区域因受载应力较大,处于63~169 MPa,其他区域的应力则相对较小,处于64 MPa以下,结构极小部分区域出现应力集中,最大应力为254 MPa。应力集中产生原因是板材连接处呈直角且离加载区较近。将最大应力数值与材料的屈服极限(345 MPa)比较,反力架在60 000 kN工况下的静强度安全系数为1.36。
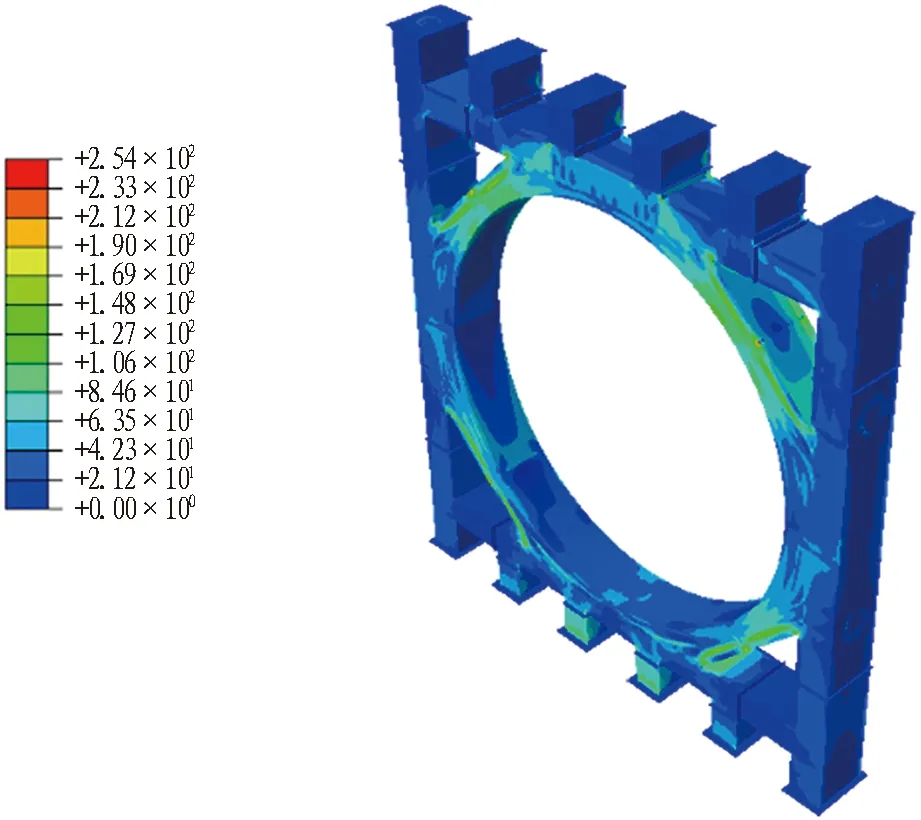
图4 反力架的等效应力云图(单位: MPa)
反力架变形云图见图5。图5中红色为变形量大的区域,最大变形量为9.57 mm,位于反力架正面板顶部(受载部位),从底部至顶部变形量呈增大趋势,因底部支座有固定连接刚度强,而上方支座未起到约束作用刚度弱,因此上部加载区产生变形较下部大。
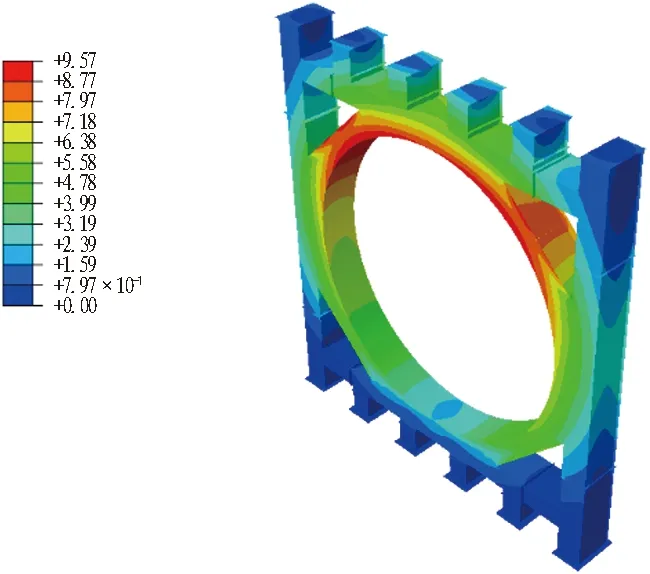
图5 反力架的变形云图(单位: mm)
依据《钢结构设计规范》[9],反力架挠度容许值要求达到重级工作制桥式起重机的水准,根据式(2)计算,只需Lk≤0.017 m(17 mm)即可。通过计算比较,反力架的变形量是符合要求的。
(2)
式中:Yb为反力架跨度,取为17 m;Lk为结构最大变形量,m。
2 结构优化方案
2.1 优化问题建立
通过改变组成反力架各部分板的厚度,实现结构整体轻量化的目标,优化过程中要保证结构的强度、刚度在要求的范围内。变量S1—S10分别为10个子区域的板厚,详细位置见图6。
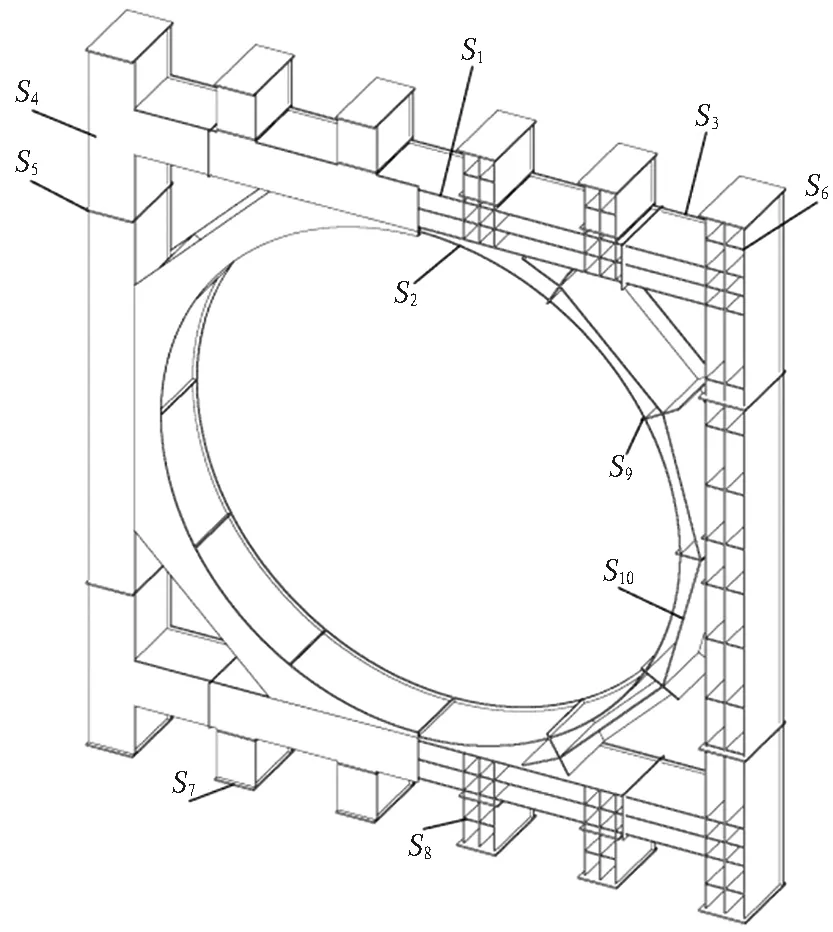
S1为筋板厚度;S2为环形腹板厚度;S3为背面板厚度;S4为正面板厚度;S5为C型连接板厚度;S6为A型连接板厚度;S7为盖板厚度;S8为B型连接板厚度;S9为环形区腹板厚度;S10为环形区加强筋厚度。
图6反力架设计变量
Fig. 6 Design variables of counterforce frame
变量S1—S10进行主效应分析时的取值范围见表3。为了寻找对结构质量贡献大的变量,按式(3)原理,利用ISIGHT进行方差分析。采用正交试验的设计方法进行实验设计[10],抽样方法为超拉丁方,共抽取20个样本,借助ISIGHT来驱动ABAQUS实现批量计算,进行主效应分析。

表3 进行主效应分析的变量及取值范围
注: 表中数字单位为mm。
(3)
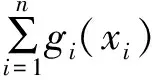
通过方差分析得到对质量贡献量较大的设计变量贡献量,见图7。选取S1贡献量为32%、S2贡献量为22%、S3贡献量为11%、S4贡献量为9%、S5贡献量为9%,一共5个参数作为本次设计的优化变量。约束条件为:σmax≤254 MPa,Lk≤13 mm。
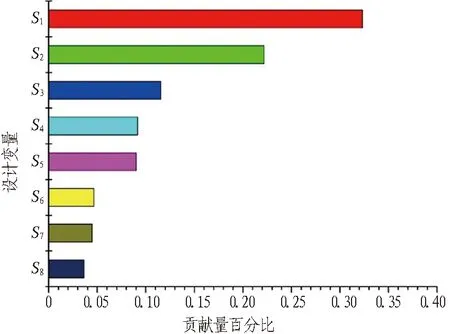
图7 设计变量对结构质量的贡献量
反力架结构优化中采用的数学公式如下:
(4)
各优化变量及其取值范围见表4。
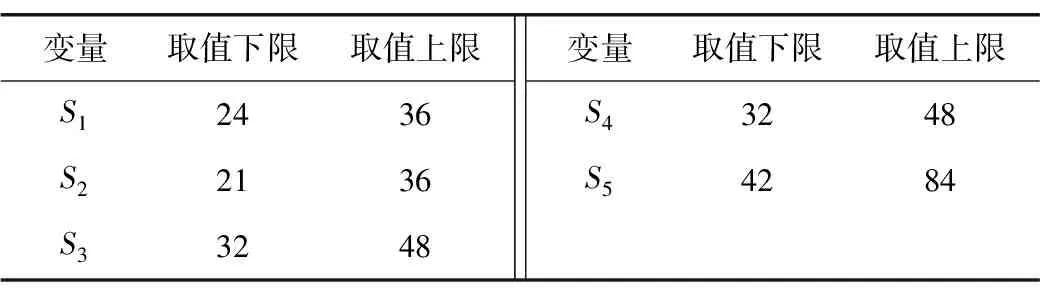
表4 各优化变量及其取值范围
2.2 优化求解策略
建立优化问题后直接求解存在计算量大、效率低的缺点,尤其是有限元求解时需要大量计算。借助近似模型的方法,通过采用拟合、插值等数值方法,将相对于变量的约束条件、目标函数重新构造,再进行数学模型上的分析,以此来减少实际模型分析时的计算量和周期,达到较简便的优化效果[11]。
反力架优化流程图见图8,采用近似模型的反力架目标设计步骤如下:
1)确定设计变量(优化变量)。
2)选择合适的试验设计方法。在设计空间中确定构造模型所用的样本点,试验设计方法通常包括全因子设计、部分因子设计、正交设计、中心组合设计和拉丁方设计等[12]。
3)利用数值计算确定样本点处的响应值,通过数值拟合构造响应值的近似模型。
4)选择合适的优化算法对近似模型进行求解。
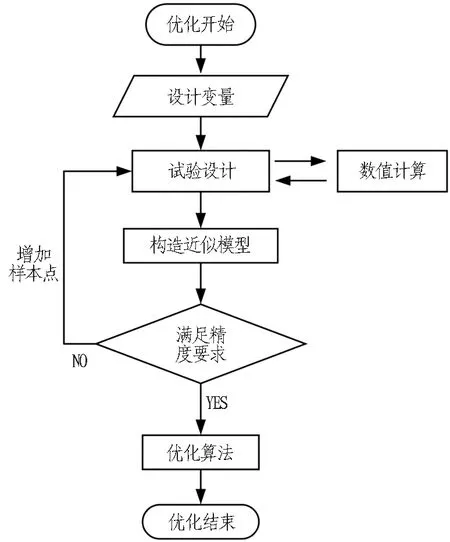
图8 反力架优化流程图
采用试验设计(DOE)作为构建近似模型的采样策略,决定了采样点的数量和空间分布[13]。为了使样本点尽可能均匀分布在设计空间,采用超拉丁方方法设计了35个样本的试验,将这些试验的计算值作为建立近似模型的基础。近似模型的拟合主要有: 克里格模型(Kriging model)、径向基函数模型(RBF model)、正交多项式模型(orthogonal polynomial model)、响应面模型(response surface model)。构造近似模型后要用复相关系数R2来检验模型是否满足精度要求[14]。R2为[0,1]的值,R2越接近1,表明模型的拟合精度越高,可信度越大,通常要求R2>0.9,构造的模型精度不够时可通过增加样本点的方法来提高。表5所示为不同近似模型下R2的值,通过对比发现径向基函数(RBF)模型拟合精度最高,R2为0.97,因此采用RBF构造近似模型。
粒子群优化算法(particle swarm optimization, PSO)是一种基于种群的随机搜索算法,具有操作简单、搜索效率高和收敛速度快等优点,适合求解混合整数非线性约束优化模型[15]。本次结构优化设计中基于PSO算法进行寻优,粒子群数取30,最大速度vmax取0.02,以避免速度过高错过最优解,经过1 501次迭代得到反力架的最轻质量。
3 方案结果对比
利用数值计算软件ABAQUS及多学科优化程序ISIGHT联合开展反力架结构轻量化设计,得到了变量及响应值在设计空间内的最优解。反力架优化前后数据对比见表6。由表6可知:S2由30 mm降至21 mm,S3由40 mm降至34 mm,S4由40 mm降至34 mm,S5由80 mm降至42 mm,反力架总质量由初始的305.78 t降至274.85 t,反力架减重10.1%(30.90 t)。
结构优化后的强度和变形云图见图9。由图9可知: 优化后结构最大应力为252.2 MPa(优化前为254 MPa),最大变形量为10.6 mm,均满足设计要求。
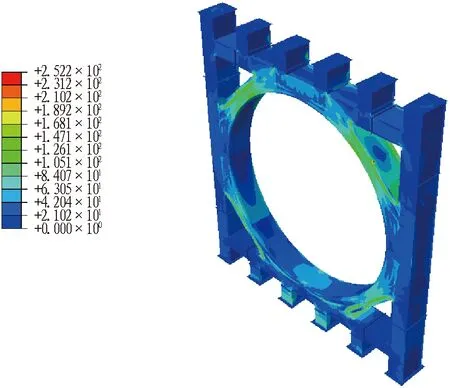
(a) 优化后的应力(单位: MPa)
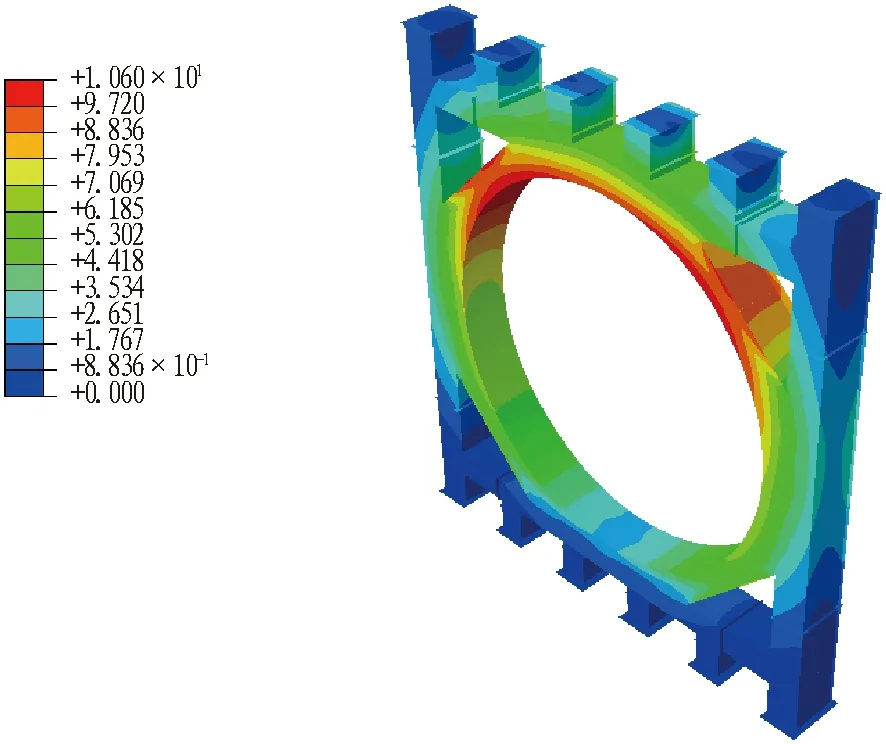
(b) 优化后的变形(单位: mm)
Fig. 9 Stress and deformation nephograms of counterforce frame after optimization
4 结论与建议
1)依据反力架结构建立了三维数值模型并开展了静力学分析,分析结果表明: 优化前结构最大等效应力为254 MPa(含应力集中点),小于材料的屈服强度(345 MPa); 结构最大变形为9.57 mm,小于控制上限(17 mm),优化前结构满足设计要求。
2)基于方差分析确定5种对结构质量贡献量大的板厚作为优化变量,以最大等效应力和最大变形作为约束条件,建立以反力架总质量最小化为目标的优化问题数学描述。
3)通过在DOE基础上建立近似模型并采用PSO算法进行求解,得到优化后结构总质量从305.78 t降至274.85 t,减重达10.1%(30.90 t),最大应力为252.2 MPa、最大变形为10.6 mm,均在要求范围之内,验证了优化方案的有效性。
4)为继续提升反力架优化设计的水平,建议利用拓扑分析方法优化结构材料的分布,在拓扑优化基础之上进行尺寸优化,将各区域板厚分别设计为优化变量,解决反力架部分子区域存在强度冗余度过高的缺点,进一步提升优化的效果。

