干雪的密度—介电常数模型的比较与评价

， ，，，

(1.山东省第七地质矿产勘查院，山东 临沂 276000； 2.贵州省质安交通工程监控检测中心有限责任公司，贵阳 550081； 3.贵州大学 资源与环境工程学院，贵阳 550025)

0 引 言

探地雷达(GPR)是研究高山积雪厚度和雪水当量(SWE)的有效工具，相比于其他技术，GPR能在有限的时间里探查更广大的区域[1-3]。与地震数据处理类似，要将雷达波的双程旅行时间转化为深度，必须要知道雷达波在介质中传播的速度，因此波速的推算就显得尤为重要。在实际应用中，可以通过设计双天线探地雷达的观测方式，并运用相应的地球物理数据的处理方法，达到测量介质中电磁波波速的目的，如共中心点法(CMP)[4]、共深度点法(CDP)[1]、偏移分析法[5]、宽角反射/折射分析法(WARR)[6]以及反射波振幅反演等[7]。另外，还有其他电磁波方法和技术，如时域反射法(TDR)和雪特性分析仪(Snow Fork)，它们可以测量探针附近一小块积雪区域的电磁波速度[8-10]，一般情况下，可以将其作为整个调查区域的电磁波波速。

除此之外，还有根据雪的密度求取波速的方法，即通过模型方程，将雪的密度与雪的介电常数联系起来[1，3，6，8-9，11]。这种方法需要明确区分雪的干、湿状态，以便准确地选择相应的方程。

在最简单的干雪状态下(仅仅是冰与空气的混合)，表征雪的介电常数和密度关系的方程也有许多种，因此选择合适的方程就有一定难度。倘若雪中还掺杂了部分水，这种三相混合的情况将会更加复杂，误差也会大大增加。此外，大多数模型方程都没有给出明确的不确定度，这会影响到对计算结果的可信度分析。

本文所研究的重点是在干雪状态下，对表征雪的介电常数和密度关系的模型方程进行比较，选出最合适的模型方程，并加以验证。

1 密度-介电常数的关系

几十年来，许多学者使用时域反射法(TDR)或频率域分析法测算干雪/湿雪的介电常数，根据雪的密度(ρ)和其介电常数(ε)的测量结果，提炼出两者之间的关系。本文将一些较为经典的ε(ρ)关系方程归纳见表1，表1中部分方程适用于湿雪状态，可以将其模型中的含水率定为零，使其适用于干雪状态[12]。

表1 雪的密度-介电常数关系

表1中雪的密度单位是g/cm3。根据表1，关系方程大致可以分为以下3类：

①线性关系：

ε=a1+a2ρ

②二次非线性关系：

ε=a1+a2ρ+a3ρ2或ε=(1+a4ρ)2

③混合规则：如文献[13]、文献[14]

相应文章的作者参考自己测量得到的数据及其他文献的数据，得到这些线性和二次非线性关系方程。一些作者通过更新测量数据，简单地修正了方程，因此表1中有些方程的常数项有许多相似之处。

大多数的文章作者都没有给出相应方程或者参数的不确定度，这限制了方程的实际应用，并使得方程之间的对比变得困难[15]。只有个别作者给出了不确定度，具体如下：

文献[17]估计ε的不确定度为±2%。

文献[18]和文献[19]的拟合曲线的标准差为0.031。

文献[20]的拟合曲线的标准差为0.006。

缺少明确的不确定度，选择哪种模型方程计算雪的介电常数就没有对比依据。

表1中的部分文章作者给出的不确定度，已在图1(b)中表示。在模型[13]、模型[14]、模型[21]和模型[22]中，冰的介电常数定为3.19±0.04[12]，冰的密度定为920±10 kg/m3[23]。由于模型[16]和模型[24]的拟合曲线基本一致，所以进行合并处理。

图1为雪的密度-介电常数关系拟合曲线。图1(a)为表1方程的拟合曲线，图1(b)是对图1(a)矩形框中的图形进行放大，以更好地展示模型[16-20]的不确定度。

从图1(b)中可以看出，Robin等的模型(黑色线，模型编号[16])可以作为最合理的选择。因为该模型的不确定度区间几乎囊括了其他模型的范围，只有模型[32]在较高的密度区间上，稍微偏离了模型[16]的不确定度区间。

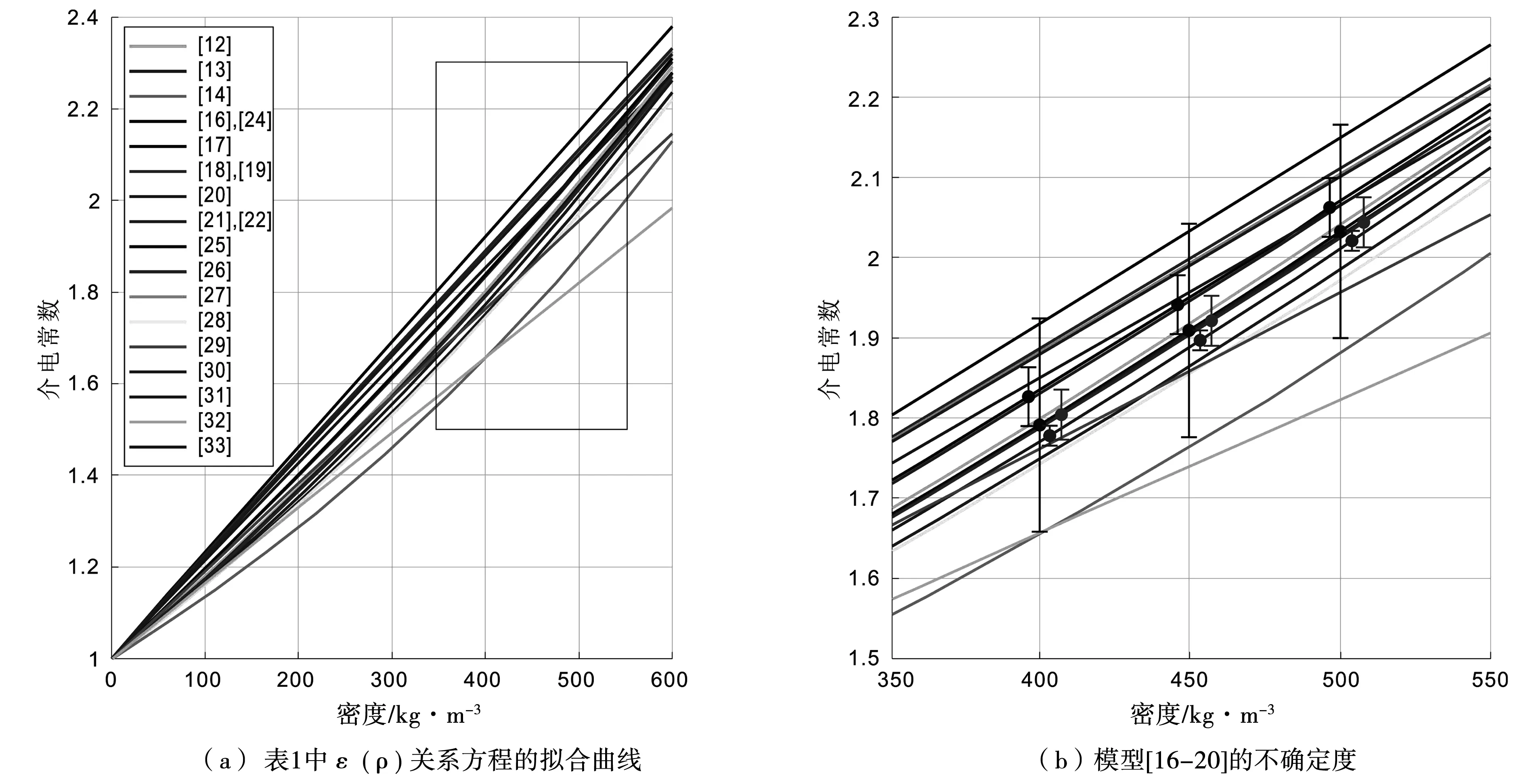
图1 雪的密度-介电常数关系拟合曲线

因此，可以选择模型[16]的方程来求取雪中的电磁波波速。

2 基于干雪的密度求取波速

使用拟合模型[16]，可以通过测得的密度值得到雪的介电常数及其不确定度，并得到雪中的电磁波波速：

(1)

式(1)中的c是真空中的光速，根据不确定度的传播率[15]，波速υ的不确定度uυ取决于以下两个因素：

①根据模型[16]得到的介电常数的不确定度：

②密度测量的不确定度：uρ

因此，可以得到波速υ的不确定度uυ为：

(2)

干雪的密度-电磁波波速关系曲线见图2，数值的计算是基于模型[16]。在图2中，左边轴表征在干雪的密度范围内，同时在模型不确定度的影响下，其电磁波波速的最大值和最小值的范围(以虚线表示)；右边轴表征波速υ的相对不确定度，可由式(2)得到。

需要注意的是，在图2中将密度测量的不确定度(uρ)定为零，因此图2中的波速υ的相对不确定度仅与拟合模型中的介电常数的不确定度(uε)有关。若代入实验数据，就需要考虑雪密度测量的不确定度，所以实测条件下，uυ将会比图2中的值更大。

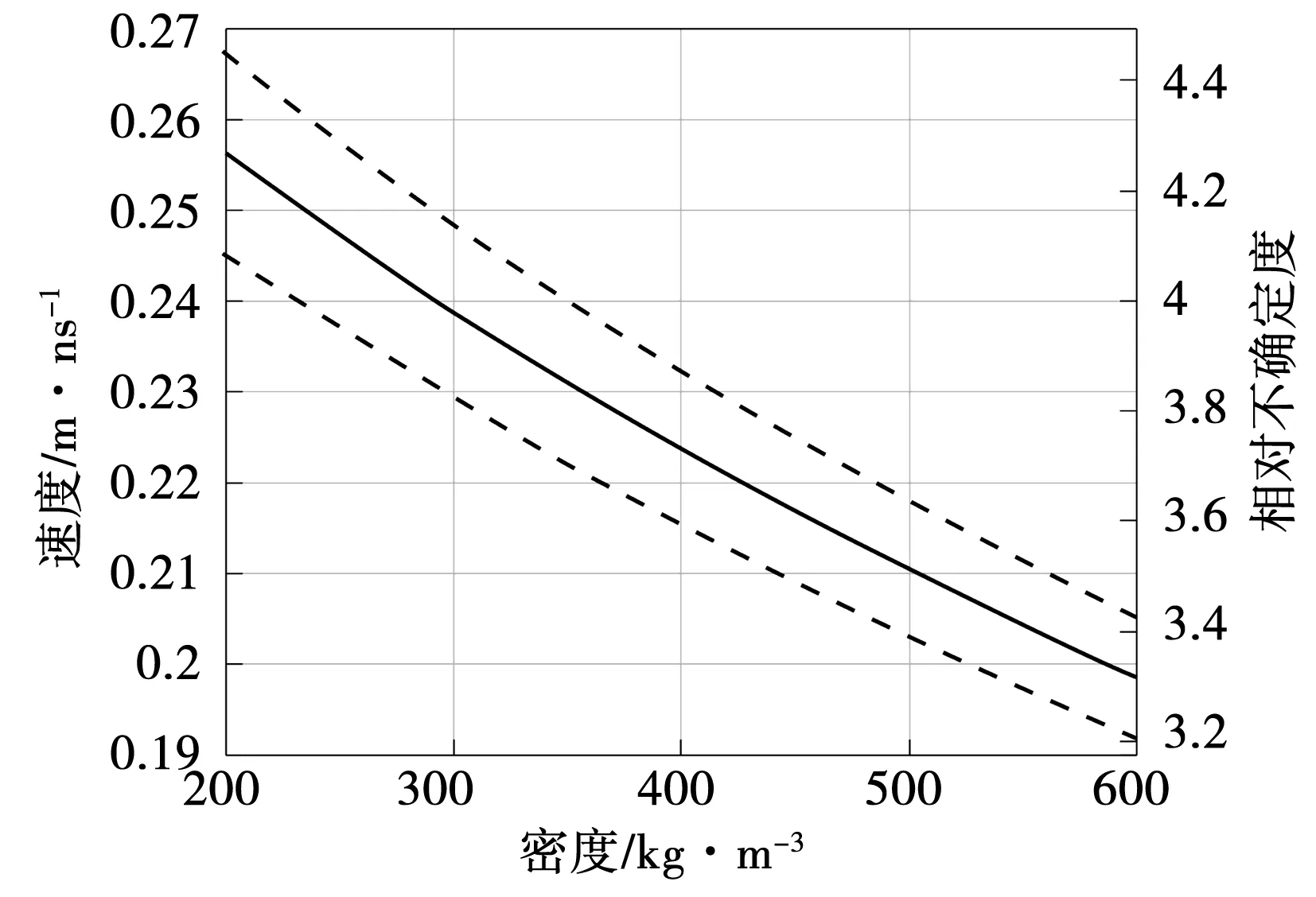
图2 干雪的密度-电磁波波速关系曲线

另外，由模型[16]得到的波速υ的相对不确定度，其量级与其他测量方法得到的波速υ的相对不确定度一致，如时域反射法(TDR)[8-9]、雪特性分析仪(Snow Fork)[10]、共中心点法(CMP)[4]、偏移分析法[5]等。

3 实验数据验证

本文所使用的数据来源于Paolo等测量的数据[9]，其数据采集自意大利阿尔卑斯山东部的Solda冰川附近，其3个采样位置(雪坑)中的雪均为干雪[9]。时域反射法(TDR)测量使用的仪器为美国泰克 Tektronix 1502C 金属电缆测试仪，所连接的3根导线探针长度为l=(30.0±2.9)mm，探针在空气中的理论特性阻抗为(165±2)Ω(计算方法见文献[34])。

实际测量时，在雪坑坑壁的不同高度，将探针水平插入进行探测。由于仪器连接的问题，在采集数据的第一天，在第一个采样坑中，只有坑壁上半部分的数据，见图3(a)。

在传输线中，信号传输的单程走时Δt可以使用导数法进行估算[20]，其波速的计算公式为：

(3)

此外，还在雪坑边缘沿垂直方向进行取芯采样，以测量积雪的密度，并得到相对连续的随深度变化的密度剖面。采样使用的是圆柱形的取样器，其底面直径为(47.00±0.29) mm，长度为(300.0±2.9) mm，每次取样的体积大约为0.5 L。测定样本质量时使用的仪器为科恩HDB 5K5N型电子钩秤，其标称精度为5 g。基于模型[16]，可以由雪坑密度随深度变化的情况，得到波速的垂直分布廓线。

图3为3个采样位置的波速垂直分布廓线。其中，蓝色点表示基于时域反射法(TDR)测量，使用式(1)计算得到的结果，黑色线表示基于取芯密度实测得到的结果。虚线表示根据式(2)得到的波速不确定度，需要指出的是，这个不确定度包含模型[16]的介电常数的不确定度和取芯密度实际测量的不确定度的影响。

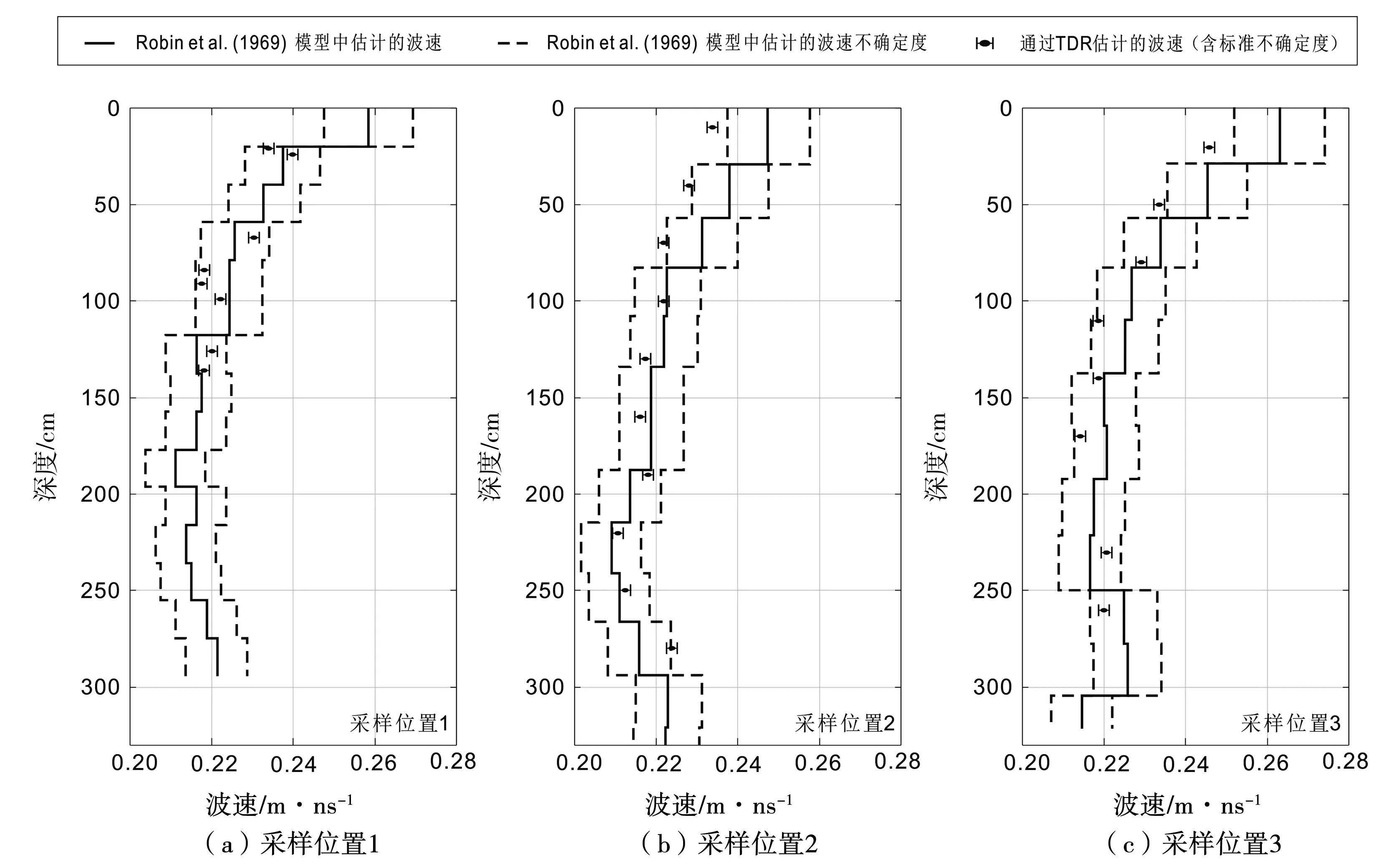
图3 3个采样位置的波速垂直分布廓线

从图3(a)-图3(c)可以知道，所有采样位置都有类似的特征，即地表附近的波速值稍高，且在深度0～150 cm的范围内，均有波速值随深度增加而下降的趋势，当深度大于150 cm时，波速值近似不变。之前的其他研究者也得出了类似的波速垂直分布廓线(如文献[1]和文献[35])。

在每个采样位置的两组数据(即TDR结果和取芯实测结果)中，它们之间差异产生可以归因于测量方法的差异。因为TDR探针在测量时是水平插入坑壁的，而对雪进行取芯采样时是沿着垂直方向的。因此，这两种方法不能同时测量同一部分雪，故而会有差异。此外，两者之间的差异主要集中于采样位置(雪坑)的表面，因为在雪坑表面。雪的孔隙度较大，所以在进行采样和测量时会出现较明显的差异。

4 结 论

通过比较不同的密度(ρ)-介电常数(ε)关系模型，基于如下两个原因，证明了Robin等给出的模型方程是其中最为可靠的一个：

①Robin模型(即模型[16])的拟合曲线位于两个极值曲线的中间(图1)。

②Robin模型(即模型[16])的不确定度区间囊括了其他模型的范围(图1)。

此外，Robin模型的不确定度的大小，与不同测量手段得到的不确定度的大小，是具有可比性的(如TDR或CMP)。在干雪上所采集到的实验数据，其结果也证明了Robin等建立的模型是合适的，最后的比较结果也有较好的一致性。