Impact of Tactical Parameters of Aircraft on Jamming Effectiveness of Surface-Source IR Decoy

Shenbo Li1, *,Qi Tong1 and Chaozhe Wang1

Abstract: As the platform for surface-source infrared decoys,the target aircraft is the aim of attacks in air-to-air combat.It can quickly and accurately evaluate the jamming effectiveness of the surface-source IR decoy in various states of motion is important for enhancing the security of the aircraft.This paper proposes a model of surface-source IR decoy,and compares and analyzes simulated and measured infrared images of diffusion.A system to assess the effectiveness of the jamming of the surface-source IR decoy,target aircraft,and infrared guided missile called “Trinity” is established.Simulations were conducted to assess the impact of flight height,flight speed,and the maneuvering of the target aircraft on the jamming effectiveness of the surface-source IR decoy.The results show that with an increase in flight height and speed,the jamming probability of a surface-source IR decoy first increases and then decreases,where evasive maneuvering by the target aircraft can effectively improve this probability.When the radius of the vertical snake maneuver was 125 m,that of the horizontal snake maneuver was 200 m, and the radius of the barrel roll maneuver was 250 m,the jamming probability of the surface-source IR decoy was relatively high.By comparing the simulation results with measured data,the study verified the accuracy of the proposed method.

Keywords:Surface-source IR decoy,tactical parameters of aircraft,jamming effectiveness,infrared countermeasures,effectiveness evaluation.

1 Introduction

Infrared decoy is one of the earliest infrared jamming equipment used in actual combats [Xu,Shi,Wang et al.(2002);Chen,Wan and Huang (2012)].Infrared decoy as a false target thrown into the air,which has certain radiation energy and infrared spectrum characteristics similar to the real target,is used to deceive or seduce the enemy’s infrared detection system and infrared guidance system.At present,it is the most widely used countermeasure with the highest cost-effectiveness to use the infrared decoy to deceive the attacking missile away from the aircraft,which is favored by all countries [Li,Wang,Yang et al.(2007)].There have been more than 70 kinds of infrared decoy equipment in service currently [Hong,Zhang and Li (2006)].

With the continual development of infrared imaging detection technology,its capabilities of target recognition,resistance to interference,all-weather combat,and guidance precision have significantly improved [Fan and Yang (2012)].Infrared imaging guidance has emerged as an important development direction in research on precision guidance [Xu,Wang and Wu (2013)].Many deficiencies have been exposed in traditional infrared decoys,and by identifying their rate of increase,trajectory,and spectrograph,the infrared detection system can distinguish between true and false targets [Zhao,Ma,Lu et al.(2012)].This requires infrared decoy technology to make continuous improvements and develop new types of IR decoy along with it.For instance,the U.S.government has invested a large amount of capital to study IR decoy since “9.11” event,and requires to carry out research on the new formula of infrared decoy [John and Neal (2011)].

Surface-source IR decoy is characterized by a large area,high efficiency,and wide spectrum.It can form an infrared radiation field with a certain intensity and area,and can change the characteristics of the target or background for jamming,which can effectively help evade infrared imaging-guided missiles [Xu,Wang and Wu (2013);Wang,Ruan and Wang (2015)].After years of development,the jamming technology of surface-source IR decoys has advanced to a high level [Li,Xie and Li (2009);Wu and Chen (2010)].Surface-source IR decoys are equipped with military platforms to effectively interfere with infrared imaging-guided missiles,and is considered an effective piece of airborne self-defense equipment.

Using only experiments to test the performance of airborne surface-type IR decoys leads to a waste of time and to increased cost.To better study jamming effectiveness,simulation and modeling are crucial.The jamming effectiveness of airborne surface-type IR decoys is influenced by many factors,such as IR radiation of airplanes and decoys,the direction of motion of the missile,and the cast of the decoy,which require a comprehensive approach.

C.R.Viau puts forward a Monte Carlo simulation evaluating effectiveness of expendable IR countermeasures against imaging IR-guided threats [Viau (2012)].Zhang et al.[Zhang,Meng,Fu et al.(2008)] proposes the anti-jamming simulation model of the imaging IR imaging guided missiles under dynamic conditions and analyzes the factors that effects the jamming capacity,such as aerial launching interval,distance,orientation,numbers and target maneuver etc.The antiaircraft simulation system that the surface-type IR decoy jam the IR imaging guided missiles is established in reference [Kong,Ma,Du et al.(2011)].Simulation of special material decoy in spatial countermeasure is realized through system of IR radiation models of airplane,IR imaging guided missile and airborne special material decoy on the basis of MJU-50/B decoy [Fu and Fang (2013)].

Most research on the jamming effectiveness of infrared decoys has focused on jamming different kinds of missiles,and no study has gauged the impact of the tactical parameters of the target aircraft.In air-to-air combat,the aircraft is the target as well as the platform for IR decoys.The quick and accurate assessment of the jamming effectiveness of surface-source IR decoys in various states of motion is important to improve the security of aircraft.Therefore,it is essential to study the impact of tactical parameters of aircraft on the jamming effectiveness of surface-source IR decoy.

In this paper,a model is proposed and simulated to study surface-source IR decoys.A motion diffusion model and an infrared image model of the chaff-type surface-source IR decoy are established.The simulation images and measured images are then compared and analyzed.We then sort and establish an effectiveness evaluation system featuring a decoy,aircraft,and missiles,and confirm the proposed method and evaluation indices.Finally,the impact of tactical parameters (flight height,flight speed,and aircraft maneuvers) on the jamming effectiveness of surface-source IR decoys is simulated and analyzed in the proposed evaluation system.

2 Model of surface-source IR decoy

The chaff-type surface-source IR decoy is manufactured by pressing more than 1,000 pieces of chaffs.Once the decoy chaff has been launched,it spontaneously combusts due to oxidation when it comes in contact with air and forms a chaff cloud cluster that approximates an ellipsoid in the air to produce surface-type infrared radiation [Guo,Wang,Huang et al.(2013)].Important characteristics of surface-source infrared decoys are related to motion and radiation,and their modeling and simulation are the basis for evaluating jamming effectiveness.The model of a surface-source IR decoy includes a motion diffusion model and an infrared image model.

2.1 Motion diffusion model

Decoy chaff is a circular sheet of very small mass,and its diffusion process in the atmosphere is greatly affected by external factors.This paper established the following hypothesis:1) the atmosphere is stationary relative to the ground,ignoring the effects of wind,2) chaff is regarded as rigid body with uniform mass distribution,3) the motion of each chaff is relatively independent without considering the collision.

In order to describe the laws of air motion of decoy chaff better,it is necessary to establish appropriate coordinates and transform the corresponding coordinates [Zou,Tong,Wang et al.(2016)].The schematic diagram of the establishment of coordinate system is shown in Fig.1.O-xgygzgis the ground coordinate system.The angle between the chaff central axis and the horizontal plane is the pitch angle of the central axisdθ.The angle between the projection of the central axis on the horizontal plane and the O-xgaxis is the deflection angle of the central axisdψ .The angle between the velocity direction of the chaff and the horizontal plane is the velocity pitch angle θ .The angle between the projection of the velocity direction of the chaff on the horizontal plane and the O-xgaxis is the velocity deflection angle ψ .O-xbybzbis the chaff’s body coordinate system,the origin is the center of the chaff.O-xhyhzhis the chaff’s track coordinate system,the origin is also the center of the chaff.And the angle between the airflow symmetry plane xbOyband the vertical plane xhOyhis the speed roll anglesγ .

The chaff moves without power during diffusion,and is under the action of only aerodynamic force and gravity.The geometry of the chaff is circular.Considering its symmetry,its aerodynamic side force can be ignored.The plane composed of the central axis of the chaff with a velocity along is its plane of airflow symmetry,and the aerodynamic drag and lift on the chaff are on the plane as well.We establish the kinetic equation of a decoy chaff in its track coordinate system O-xhyhzh:

where m is the chaff’s mass;X is aerodynamic drag;Y is aerodynamic lift;xc andyc are aerodynamic coefficients;ρ is atmospheric density;and S is the area of the chaff.According to the conversion relationship in geometry,the speed roll anglesγ of the chaff can be calculated based on the speed of the motion of the center of mass of the decoy chaff and its attitude of the decoy chaff.The direction of velocity of the chaff is determined by the velocity pitch angle θ and velocity deflection angle ψ ,and its attitude is determined by the pitch angle of the central axisdθ and the deflection angle of the central axisdψ :

The kinematic equation of the center of mass of the chaff is:

Due to the particularity of the shape of the chaff,its rotation can be seen as the rotation of two attitude angles along the center:

whereωzbis rotational angular velocity of the pitch angle of the central axis;andωxbis rotational angular velocity of the angle of deflection of the central axis.To simplify the calculation and analysis,it is assumed thatωzband >ωxbdo not change with time.

After setting the initial position of the chaff,the initial velocityV0,the directions of initial velocityoθandψo,the initial attitudes of the chaffθ0dandψ0d,and the rotational angular velocityωzbandωxb,by integrating Eqs.(1),(5) and (6),the flight trajectory of the chaff can be obtained.

The law of motion of the spatial diffusion of surface-source infrared decoy can be summarized by setting the probability distribution of the initial attitude,velocity,and rotational angular velocity of thousands of decoy chaffs and solving their equations of motion [Zou,Tong,Wang et al.(2016)].

A decoy usually contains more than 1,000 chaffs that are compactly laminated.According to analyses of the characteristics of the internal ballistics in Huang et al.[Huang,Zhao and Du (2011)],there are subtle differences in the outlet velocities of the chaffs,where this an acceleration process in the launching cylinder.The first piece has the lowest velocity and the last piece has the highest.Based on the analysis of the simulation results and experimental data,it can be concluded that the outlet velocityV0of the chaffs follows a uniform distributionU(25,35).Due to the influence of random factors,such as atmospheric disturbances,the initial attitudes of the more than 1,000 chaffs are also different.It can be assumed that the initial pitch angleθd0of the center axis of the chaff follows the normal distributionN(π/ 2,π2/300) and the initial deflection angleψd0of the center axis of the chaff follows the normal distributionN(π/ 2,π2/500).When the chaff has completely combusted,it begins rotating under aerodynamic and combustion forces.Given that aerodynamic effects and combustion conditions are somewhat random,the rotation angular velocities of the chaffs are different.It is assumed that both the rotational angular velocityωzbof the pitch angle of the chaff’s center axis and the rotational angular velocityωxbof its deflection angle follow the uniform distributionU( -1 6π,16π).Finally,the diffused image of the surface-source IR decoy can be obtained by solving the equations.

2.2 Infrared image model

After solving for the temperature field and radiance of the decoy chaff’s surface [Mokry (2001);Wilharm (2003)],we use the bottom-up dynamic programming method to solve the optimization problem of the total radiation intensity of the surface-source IR decoy.We briefly introduce the solution to the bottom-up dynamic programming method as shown in Fig.2 [Cormen,Leiserson,Rivest et al.(2015)].

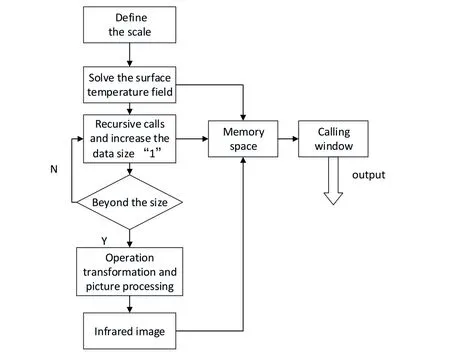
Figure 2:The solving process of combustion optimization algorithm

1.Set the scale of quantity of surface-source IR decoy.In algorithm optimization,set the number of chaffs to 1,000 pieces to make the number consistent with that in the simulation or experiment.If solving for a larger decoy chaff group,it is necessary to only adjust the initial scale of decoy chaffs.

2.Define the minimum scale of solution of the sub-problem as the temperature field of the surface of the single-decoy chaff.We have solved for the decoy chaff in the previous section.The results are saved in the corresponding storage space,and can be called directly to improve operational efficiency.

3.We increase the scale by one each time through recursive calls,and the solved temperature field distributions of sub-problem scale are all saved,and can be called directly.The sub-problems of the same type need only be solved once without repeated processing.When the data scale does not reach that initially set,we continue the recursive call until the scale of the sub-problem is identical to that defined in the initial scale,terminate the recursive call,and return to the temperature field that has been finally solved.

4.Through post-stage operation conversion and image processing,we generate the infrared diffusion images of decoys distributed in the space.

5.When it is necessary to call the solution of a certain scale,we call it through the set call window.

Initial conditions:Set one surface-source IR decoy with 1,000 chaffs,with the mass of a single decoy chaff set to 0.65g,diameter to 25.4mm,and the initial separation time to 0.36s.Launch the chaffs at an angle of 75°,and set the velocity of the launch platform to 0.6Maand the height of the launch point to 3.5m.Figs.3,4,and 5 show the contrast sequences of the simulated image and the measured infrared image when the surfacesource IR decoy is 0.5s,1.0sand 1.5s,respectively.

It is clear the image sequences that the diffusion image and the test image of the surfacesource IR decoy obtained by simulation were consistent in terms of diffusion shape and radiance,which also reflects the correctness of the optimization algorithm in the infrared image model.

Figure 3:Decoy’s infrared image of simulation and experiment at 0.5 s

Figure 4:Decoy’s infrared image of simulation and experiment at 1.0 s

Figure 5:Decoy’s infrared image of simulation and experiment at 1.5 s

3 Effectiveness evaluation system

The overall structure of the effectiveness evaluation system is shown in Fig.6.It contains two main modules.The simulation module contains an aircraft simulation model,a surface-source IR decoy model,and an infrared-guided missile model.The evaluation module consists of an effectiveness evaluation model and the results,the latter of which cater to the jamming effectiveness and jamming strategy of decoys in different situations.The entire system also contains two independent modules.A database is used to provide all initial data needed for the operation of the other modules,and a combat scenario module is used to set the battlefield scenario,environmental parameters,and interference control parameters to complete system initialization.

Figure 6:The overall structure of the effectiveness evaluation system

3.1 Simulation module

The model of the target aircraft

In general,the motion of the aircraft can be determined by solving a six-degree-offreedom equation.However,it is difficult to obtain the parameters and the solution is complex,which affects the efficiency of simulation.In this paper,typical aircraft flight parameters were collected.By interpolating and fitting data relating to the flight parameters,an aircraft fight database was established and the trajectory was obtained,which improves simulation efficiency and ensures the authenticity of the results.

The radiation characteristics of aircraft have been analyzed in detail in Li et al.[Li,Tong,Huang et al.(2017);Zhou,Wang and Li (2017)],in which models of the infrared radiation-related characteristics of the jet nozzle,tail flame,and skin of the airframe have been developed and,through simulation analysis,have been verified.

The model of IR guided missile

The simulation of the guided missile included a recognition mechanism for the seeker and anti-jamming simulation,a guidance method simulation,a control simulation,and a motion equation [Tong,Li,Liu et al.(2008);Lv,Huang and Ling (2004)].

3.2 Evaluation module

In the simulation,the guidance error of the missile was characterized by miss distance,as shown in Fig.7.Without considering the influence of system errors,the miss distance obtained in the simulation was the algebraic sum of the interference error and random error [Tong,Li,Tong et al.(2015)].We selected the miss distance of the missile as the index of the effectiveness of the combat evaluation of surface-source IR decoys.The miss distance is the mathematical expectation of the miss distances in multiple simulations.

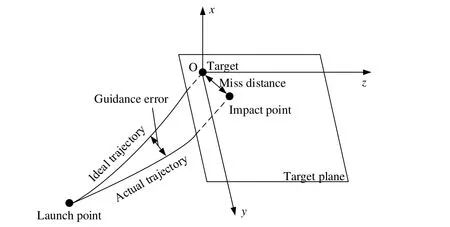
Figure 7:Schematic diagram of miss distance

When the missile exploded,the coordinates of aircraft’s center of mass ( ,,)X Y Zand the coordinates of missile’s center of mass (x,y,z)are given,the missile’s miss distanceR′ is as follow.

In consideration of geometrical shape of the aircraft,the missile’s miss distanceRafter correction is:

Where (L,H,W) shows the aircraft length,height and wingspan respectively.

If missile’s miss distance is bigger than effective killing distance of the missile,the missile can’t hit the target and the decoy jamming is success.Judge whether the jamming is successful or not by calculating the size of miss distance,count the number of times of successful jamming and obtain the probability of successful jamming of surface source IR decoy.

4 Selection of tactical parameters of aircraft

(1) Flight height:The density of air changes with the altitude of the target aircraft.Because the volume of the decoy chaff is relatively small,motion tracking in the diffusion process is easily affected by airflow.The air temperature at different heights was also different,and affects the combustion efficiency of the decoy chaffs.

(2) Flight speed:The change in the speed of the target aircraft affects the infrared radiation characteristics of its skin [Li,Tong,Huang et al.(2017)].The higher its speed,the more intense the heat exchange between the airframe skin and the atmosphere,and the higher the surface temperature of the skin.

(3) Maneuver:Maneuvering of the aircraft enables it to evade attacks [Zhong,Liu,Yang et al.(2008)].Under different scenarios involving missile attacks,the target aircraft maneuvers to evade while releasing surface-source IR decoys to gain more time.

5 Simulation analysis

5.1 Impact of flight height

The initial conditions were set as follows:the target aircraft maintained level flight,and the flight speed was 0.7Ma.The missile was a third-generation missile with a speed of 1.2Ma.The infrared seeker used a cross-detector with a tracking field angle ofφ1= 80° and an instantaneous field angleφ2=3°.The distance between the missile and the aircraft was 5,000mat the same height.Once the missile had locked onto the target,the target aircraft launched a surface-source IR decoy at a launch angle of 80° and launch speed of 30m/s.In the simulation,the height of the target aircraft was altered to 4,500m,5,000m,7,000m,and 9,000m,the jamming probability of the decoy was calculated,and the relationship between flight height and jamming effectiveness was examined.

Figs.8~11 show images of infrared counteraction when the target aircraft was at 4,500m,5,000m,7,000m,and 9,000mrespectively.As shown in the images,successful jamming became very likely when a surface-source IR decoy was released at a height below 9,000m.

Figure 8:Flight height of 4,500 m

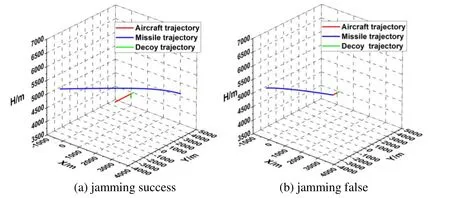
Figure 9:Flight height of 5,000 m

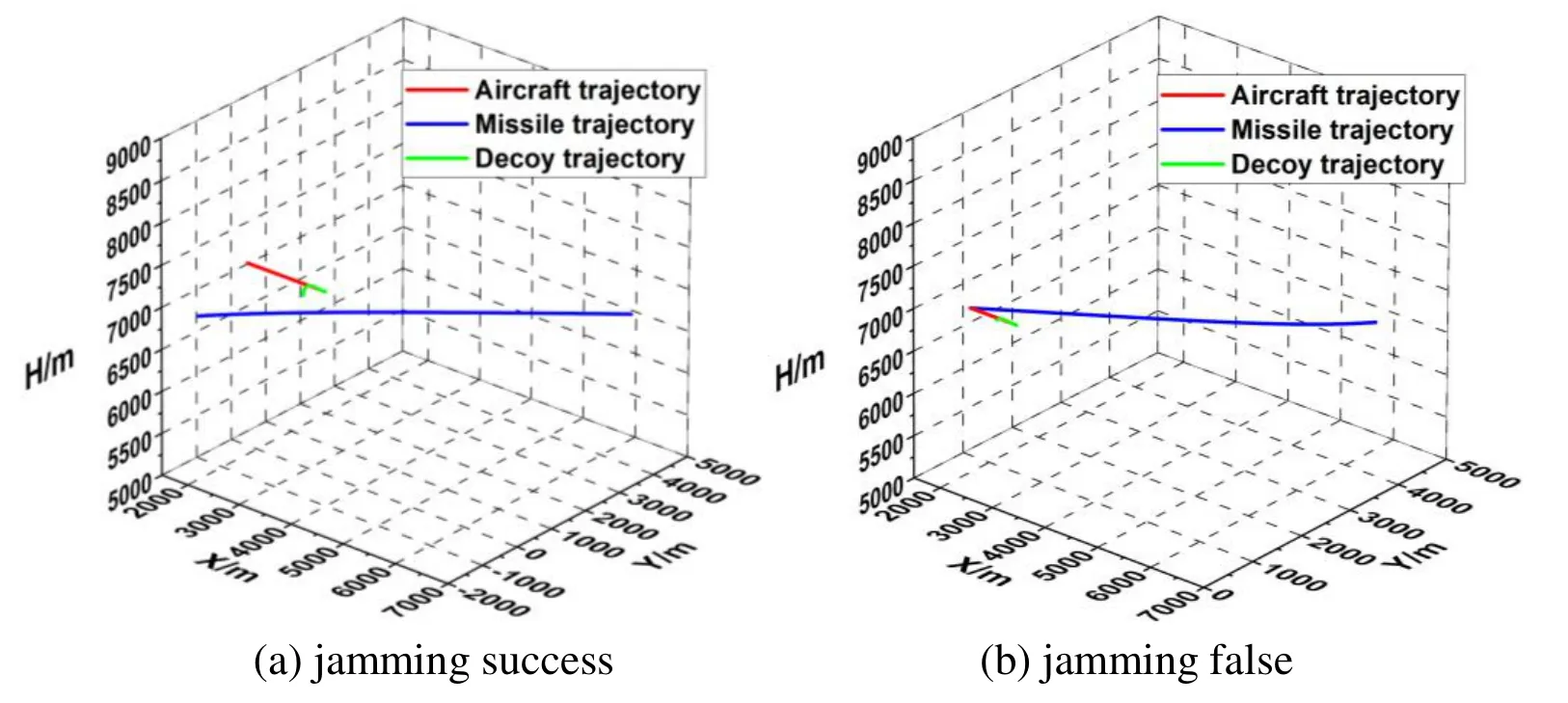
Figure 10:Flight height of 7,000 m

Figure 11:Flight height of 9,000 m

The missile attacked at a side-front angle of 135 ,and was simulated 3,000 times under the same conditions to obtain the probabilities of jamming it using the surface-source IR decoy at heights of 4,500m,5,000m,7,000m,9,000m,10,000m,and 11,000mas shown in Tab.1.The results coincide with experimental measurements.Different heights affect the degrees of diffusion of the surface-source IR decoy,which influenced their jamming probability to a certain extent.

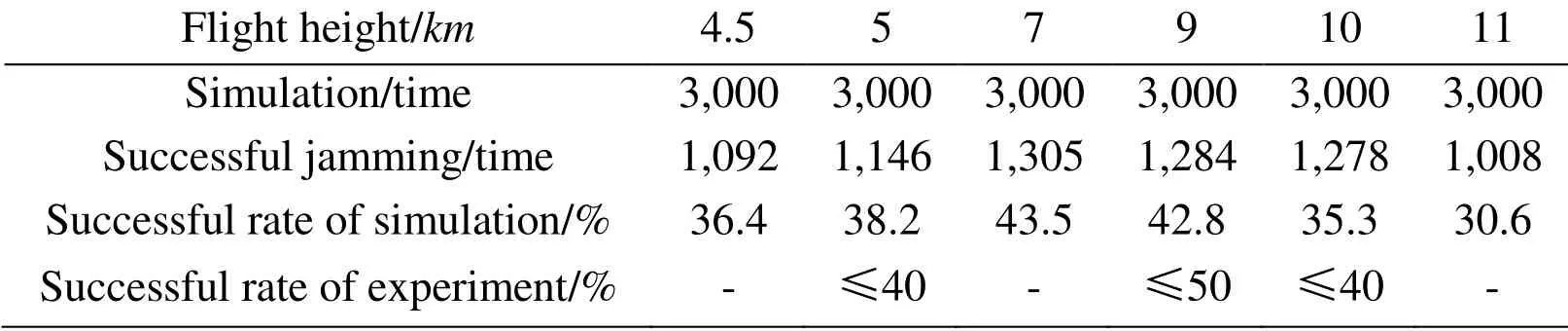
Table 1:Successful jamming probability of simulation

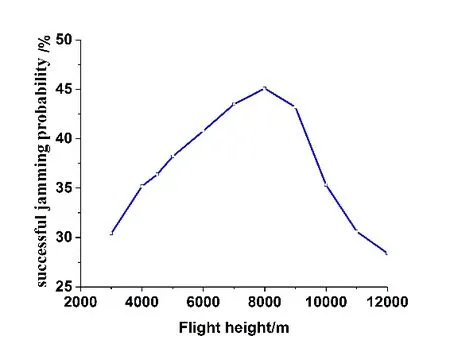
Figure 12:The relation diagram of successful jamming probability and flight height

We analyzed the simulation of the jamming probability of the surface-source IR decoy at different altitudes using the same method,conducted data fitting to the summarized jamming probabilities,and obtained a relationship diagram,as shown in Fig.12.It is clear here that with an increase in height,the jamming probability of the surface-source IR decoy increases gradually,reaches the maximum value at around 8,000m,and quickly decreases.This is because with an increase in flight height,the density of the atmosphere decreased,as did the atmospheric pressure and temperature,and the aerodynamic force of the decoy chaff during motion changed.When the height was low,the diffusion of the decoy chaffs was relatively dispersed.Although the degree of diffusion was adequate,the aerodynamic drag was relatively large,the settlement was comparatively quick,and the effective duration was extremely short.When the height was relatively high,the density of the atmosphere was small.Although chaffs are subject to relatively small aerodynamic drag and their settlement is slow,the chaff cloud did not completely disperse,and could not effectively shield the target aircraft.At a height of around 8,000m,the decoy chaffs were fully dispersed and the settling velocity was moderate.They effectively shielded the tail of the aircraft.The duration was comparatively long and the jamming probability was high.

5.2 Impact of flight speed

The initial conditions were set as follows:The target aircraft maintained level flight at 9,000m.The missile was third generation,and the distance between it and the aircraft was 5,000mat the same height.The missile attacked the aircraft from a right-sided direction angle of 90°.Once it had locked the target,the target aircraft launched a surface-source IR decoy at an angle of 80° and a launch speed of 30m/s.By changing the speed of the target aircraft to 0.5Ma,0.6Ma,0.7Ma,and 0.9Ma,we calculated the jamming probability of the surface-source IR decoy,and determined the relationship between flight speed and the effectiveness of jamming of the decoy.

Figure 13:The third generation missile incomes from the right-side

Fig.13 shows the infrared counteraction of the target aircraft at different speeds when the third-generation missile attacked at a right-sided angle of 90°.The target aircraft released the surface-source IR decoy in this case but the jamming probability was not high because the infrared radiation intensity of the aircraft on the right side was relatively high,and could be more easily captured by the seeker.With an increase in speed of the target aircraft,the rate of change of the tracking angle of sight of the missile gradually increased,but did not exceed the threshold.The missile could distinguish between true and false targets using the motion characteristics of the target aircraft and the decoy.

We performed the above simulation 3,000 times under the same conditions and obtained the jamming probability of the surface-source IR decoy,as shown in Tab.2.The statistical results are in agreement with the measured ones.Different flight speeds affected the degrees of separation between the chaff cloud of the surface-source IR decoy and the target aircraft,which to some extent influenced its jamming probability.

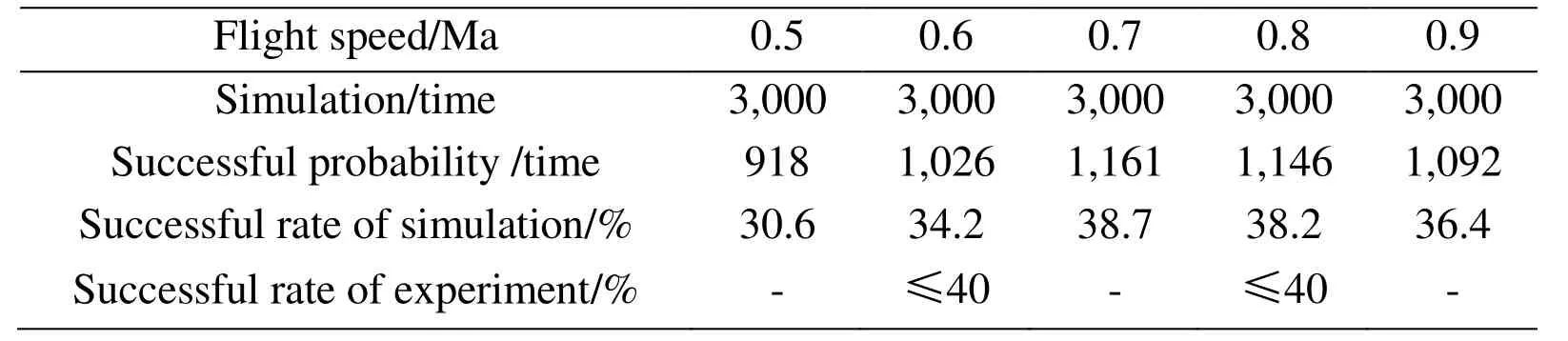
Table 2:Successful jamming probability of simulation

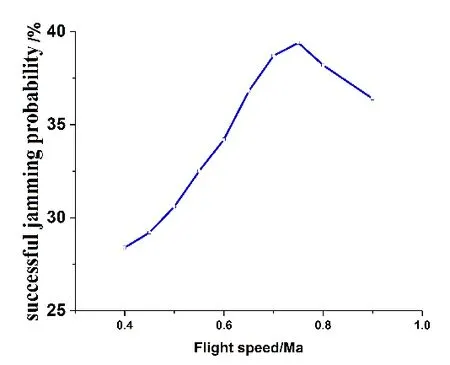
Figure 14:The relation diagram of successful jamming probability and flight speed

We conducted a simulation analysis of the jamming probability of the surface-source IR decoy at different flight speeds using the same simulation method,fitted the data to the summarized jamming probabilities,and obtained a relationship diagram,as shown in Fig.14.With an increase in flight speed,the jamming probability of the IR decoy increased gradually,reached the maximum value at around 0.75Ma,and dropped.This is because with the increase in flight speed,the intensity of friction-based heat exchange between the aircraft’s skin and the air increased,the temperature of the aircraft’s skin rose rapidly as the intensity of infrared radiation increased.At a flight speed of 0.7~0.8Ma,the average radiation intensity of the aircraft’s skin and the chaff cloud of the surface-source IR decoy reached the same order of magnitude.The launching of the decoy enhanced the jamming probability to some extent.With a change in flight speed,both the temperature of the aircraft’s skin and radiation intensity underwent changes,and the seeker was able to distinguish between infrared radiation images of the chaff cloud and the target aircraft easily.

5.3 Impact of aircraft’s maneuver

The initial conditions were set as follows:The missile was third generation,and attacked the aircraft from the right side at angle of 90°,and there was no difference in height between it and the initial height of the target aircraft.Once the missile had locked the target,the target aircraft launched a surface-source IR decoy at an angle of 80 and launch speed of 30m/s.The target aircraft then made vertical and horizontal snake maneuvers at radii of 125mand 300m,respectively,and a barrel roll maneuver at radii of 125mand 250m.We calculated the jamming probability of the surface-source IR decoy,and examined the relationship between the maneuver and the effectiveness of jamming by the decoy.

Fig.15 shows a schematic diagram of infrared counteraction when the target aircraft performed the snake maneuver in the vertical direction at radii of 125mand 300m.In Fig.15(a),the aircraft snakes vertically at a minor radius at a height of 9,000m,which is close to the optimal height for effective jamming.In the maneuvering of the target aircraft,the missile constantly adjusted its tracking field angle,and was involved in a corresponding maneuver.While the surface-source infrared decoy was released,the tracking field angle of the missile changed more significantly.In Fig.15(b),the target aircraft performs the snake maneuver vertically at a major radius at 11,000m,which is far from the best height for effective jamming.It is clear that the tracking field angle of the missile in (b) changes steadily.

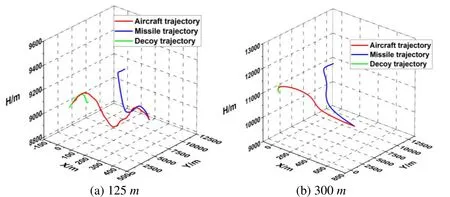
Figure 15:Vertical snake maneuver

We simulated the attack of the third-generation missile from the right side at an angle of 90° at a height of 9,000m3,000 times under the same conditions,and obtained the jamming probability of the surface-source IR decoy as shown in Tab.3.Different maneuver radii affected the maneuvering overload of the attacking missiles to a significant extent,which determined the jamming probability of the surface-source IR decoys.

Table 3:Successful jamming probability of simulation

We conducted a simulation analysis of the jamming probability of surface-source IR decoy under different maneuver radii using the same simulation method,fitted the data to the summarized jamming probabilities,and obtained a relationship diagram as shown in Fig.16.The jamming probability of the surface-source IR decoy in the rear was slightly greater than that in the front because the radiation intensity of the exhaust system played a dominant role when the missile attacked from the rear.When the target aircraft performed the snake maneuver vertically,it efficiently reduced the effective radiation area of the exhaust system,released the surface-source IR decoy,and thus enhanced the jamming probability.Conversely,when the missile attacked from the front,the vertical snake maneuver increased the effective radiation area of the exhaust system and decreased the jamming probability.The smaller the radius of the vertical snake maneuver,the faster the maneuver overload of the missile changes,and the higher the jamming probability.

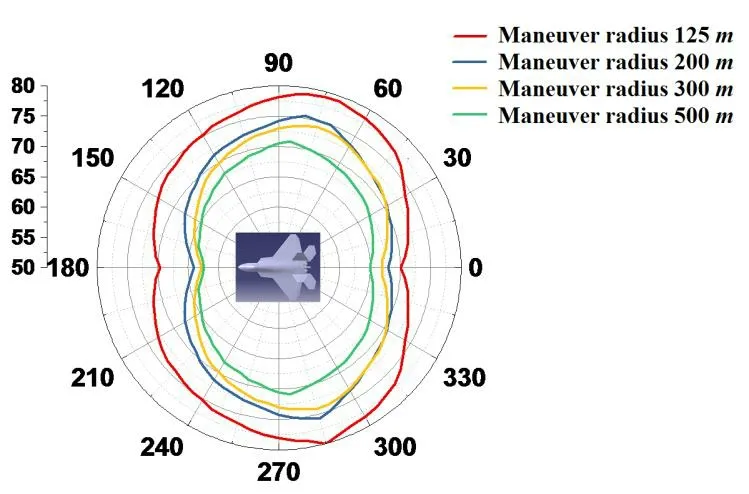
Figure 16:The relation diagram of successful jamming probability and the radius of vertical snake maneuver

Fig.17 shows a schematic diagram of infrared counteraction when the target aircraft performed the snake maneuver in the horizontal direction at maneuver radii of 125mand 300m.In Fig.17(a),the aircraft performs the snake maneuver horizontally with a minor radius at a height of 8,000m,close the best height for effective jamming.In the maneuver process of the target aircraft,the missile constantly adjusted flight attitude,and when the surface-source IR decoy was released,the tracking filed angle of the missile changed significantly.In Fig.17(b),the target aircraft performs the snake maneuver horizontally with a major radius at the same flight height as the target aircraft in Fig.17(a),and it is clear that the field angle of the missile in Fig.17(b) does not change as steadily as that in Fig.17(a).

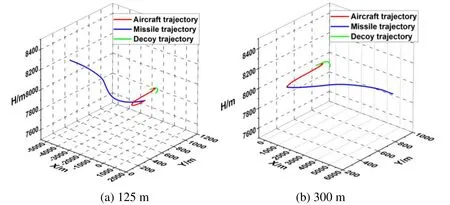
Figure 17:Horizontal snake maneuver

We simulated the attack by the missile from the right at an angle of 90° at a height of 8,000m3,000 times under the same conditions,and obtained the jamming probability of surface-source IR decoy as shown in Tab.4.Different maneuver radii affected the rates of change of the tracking field angles of the missile to a great extent,and determined the jamming probabilities of the surface-source IR decoys.

Table 4:Successful jamming probability of simulation

We conducted a simulation analysis of the jamming probability of the surface-source IR decoy under different maneuver radii using the same simulation method,fitted the data to the summarized jamming probabilities,and obtained a relationship diagram,as shown in Fig.18.It is clear that the jamming probability of the surface-source IR decoy in the rear was slightly smaller than that at the front because when the missile attacked from the rear and the target aircraft performed the horizontal snake maneuver,two situations could occur.First,the aircraft performed the snake maneuver away from the missile,which increased the effective radiation area of the exhaust system.Second,the aircraft performed the horizontal snake maneuver toward the missile,which reduced the time for the seeker to adjust the field angle.In the above two situations,the jamming probability of the surface-source IR decoy was slightly lower than that in the front.When the radius of the horizontal snake maneuver was 200m,the jamming probability of the surfacesource IR decoy was high because when the radius of maneuvering was too small,the effective shielding time of the released surface-source IR decoy was short.When the radius of maneuvering was too large,the missile could adjust the tracking field angle in time to strike the target.

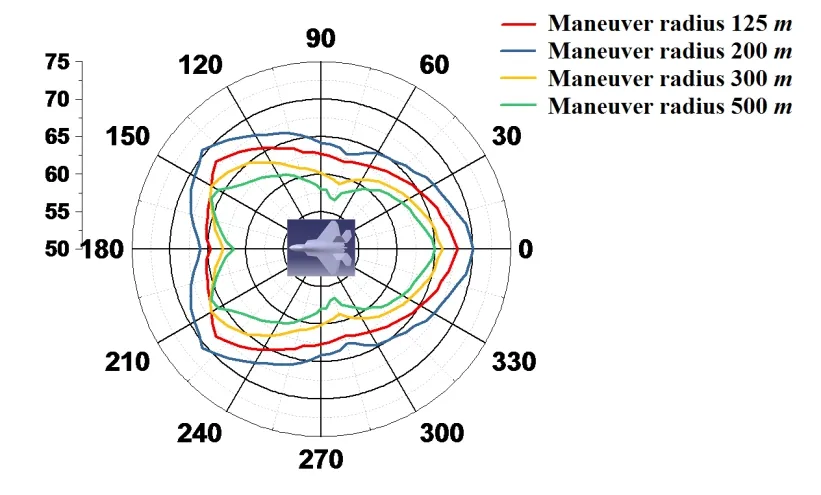
Figure 18:The relation diagram of successful jamming probability and the radius of horizontal snake maneuver

Fig.19 shows a schematic diagram of infrared counteraction when the target aircraft performed the barrel roll maneuver at radii of 125mand 250m.

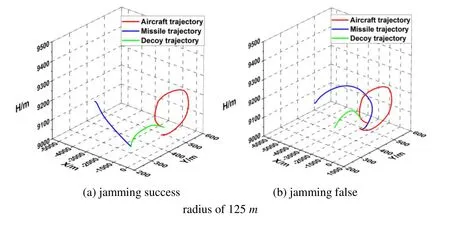
Figure 19:The radius of barrel-roll maneuver is 125 m and 250 m

We simulated the attack by the missile from the right at an angle of 90° at a height of 9,000m3,000 times under the same conditions,and obtained the jamming probability of the surface-source IR decoy as shown in Tab.5.Different maneuver radii affected the rates of change of flight overloads and tracking field angles of the attacking missiles to a great extent,and this determined the jamming probabilities of the surface-source IR decoys.

Table 5:Successful jamming probability of simulation

We conducted a simulation analysis of the jamming probability of the surface-source IR decoy in different directions using the same simulation method,fitted the data to the summarized jamming probabilities,and obtained a relationship diagram as shown in Fig.20.The jamming probability of the surface-source IR decoy in the rear was higher than that in the front,especially along the right-rear direction,where the jamming probability was the highest.This is because when the missile attacked from this direction or near it,the infrared radiation intensity of the exhaust system of the target aircraft played a dominant role,where this is the radiation source that the seeker mainly tracks.When the target aircraft performed the barrel roll maneuver,this rapidly reduced the effective radiation area of the exhaust system and caused the surface-source IR decoy to launch at the same time.The missile might have continued to track the released chaff cloud as the new goal,and the target aircraft would have quickly maneuvered away from the focal plane of the seeker.When the maneuver radius of the barrel roll was 250m,the jamming probability of the surface-source IR decoy was relatively high because when the radius of maneuvering was too small,the effective shielding time of the surface-source IR decoy was relatively short.When the radius of maneuvering was too large,the missile could not be effectively separated from the range of the focal plane of the seeker.

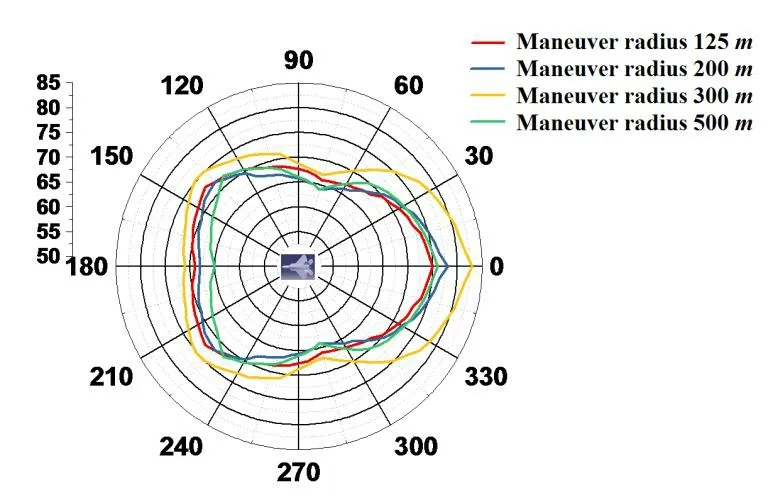
Figure 20:The relation diagram of successful jamming probability and the radius of barrel-roll maneuver

6 Conclusions

This paper conducted out simulation analyses of the impact of the tactical parameters of an aircraft on the jamming effectiveness of its surface-source IR decoy,and compared the results with the statistical results of experiments.The results were found to be credible and effective within the range of error.The main conclusions are as follows:

(1) With an increase in flight height,the successful jamming probability of the surfacesource IR decoy increased gradually,reaching the maximum value at around 8,000m,and quickly decreasing.

(2) With increase in flight speed,the successful jamming probability of the surfacesource IR decoy increased gradually,reached the maximum value at around 0.75Ma,and began to drop.

(3) Evasive maneuvers by the target aircraft can enhance the successful jamming probability of the surface-source IR decoy.When the maneuvering radius of the vertical snake maneuver was 125m,that of the horizontal snake maneuver was 200m,and the maneuver radius of barrel roll was 250m,the successful jamming probability of the surface-source IR decoy was relatively high.

Declaration of Conflicting Interests:The author(s) declared no potential conflicts of interest with respect to the research,authorship,and/or publication of this article.

Acknowledgement:This work is supported by the National Natural Science Foundation of China (No.61471390).

References

Chen,N.;Wan,C.;Huang,F.(2012):Interference availability of IR surface-type decoy.Aerospace Electronic Warfare,vol.28,no.6,pp.38-42.

Cormen,T.H.;Leiserson,C.E.;Rivest,R.L;Stein,C.(2015):Introduction to Algorithm.China Machine Press,Beijing.

Fan,J.X.;Yang,J.Y.(2012):Development trends of infrared imaging detecting technology.Infrared and Laser Engineering,vol.41,no.12,pp.3145-3153.

Fu,X.H.;Fan,Q.L.(2013):Research on modeling and simulation of special material decoy.Electro-Optic Technology Application,vol.28,no.6,pp.81-86.

Guo,B.T.;Wang,X.R.;Huang,X.;Liu,D.L.;Chai,G.B.(2013):Modeling and simulation of the scattering of targets surface by infrared decoys radiation.Infrared and Laser Engineering,vol.42,no.2,pp.300-304.

Hong,Y.;Zhang,K.;Li,Y.J.(2006):Simulation and jamming model of infrared bait.Journal of System Simulation,vol.18,no.2,pp.463-466.

Huang,C.Q.;Zhao,H.;Du,H.W.(2011):The Precision Guidance Theroy of Airborne Mention.National Defense Industry Press,Beijing.

John,F.;Neal,B.(2011):The US IR decoy industry:planning for a viable future.Journal of Electronic Defense,vol.4,no.34,pp.35-37.

Li,B.N.;Xie,J.P.;Li,C.R.(2009):Development analysis of the US surface-type infrared decoy.Ship Electronic Engineering,vol.29,no.7,pp.33-35.

Li,T.R.;Tong,Z.X.;Huang,H.S.;Wang,C.Z.;Li,S.B.(2017):Study on infrared radiation characteristic of aircraft.Laser ＆Infrared,vol.47,no.2,pp.189-194．

Li,W.H.;Wang,Q.L.;Yang,C.Z.;Li,Y.Z.(2007):Study of airborne infrared bait and countermeasures to air-to-air missile simulation.Microcomputer Information,vol.23,no.10,pp.196-197.

Lv,X.Y.;Huang,C.C.;Ling,Y.S.(2004):Analysis on surface-type infrared decoy for jamming infrared imaging guidance.Electronic Warfare Technology,vol.5,pp.41-45.

Mokry,M.(2001):Numerical simulation of aircraft trailing vortices interacting with ambient shear or ground.Journal of Aircraft,vol.38,no.4,pp.636-643.

Kong,X.L.;Ma,S.X.;Du,Y.P.;Lin,T.(2011):Simulation research on surface-type infrared decoy for jamming infrared imaging guided missile.Command Control ＆Simulation,vol.33,no.1,pp.78-81.

Tong,Q.;Li,J.X.;Tong,Z.X.;Xu,A.;Jia,L.T.et al.(2015):Combat operational method of airborne infrared decoy.Infrared and Laser Engineering,vol.44,no.2,pp.419-427.

Tong,Z.X.;Li,C.L.;Liu,P.F.(2008):Digital modeling theories and methods of infrared system attack-defend confront.Journal of System Simulation,vol.20,no.22,pp.6042-6045.

Viau,C.R.(2012):Expendable countermeasure effectiveness against imaging infrared guided threats.Second International Conference on Electronic Warfare.

Wang,Z.W.;Ruan,W.J.;Wang,H.(2015):Simulation of plates group initial separation in high speed.Acta Aerodynamica Sinica,vol.33,no.6,pp.828-834.

Wu,T.;Chen,L.(2010):Development trend of the image type infrared decoy technology.Ship Electronic Engineering,vol.30,no.5,pp.31-34.

Wilhram,C.K.(2003):Combustion model for pyrophoric metal foils.Propellants,Explosives,Pyrotechnics,vol.28,no.6,pp.296-300.

Xu,B.;Shi,J.M.;Wang,J.C.;Yuan,Z.C.(2002):The jamming technology and development tendency of IR guided weapons.Aerospace Electronic Warfare,vol.6,pp.29-32.

Xu,H.L.;Wang,J.;Wu,X.F.(2013):Research into the jamming of distributed surface type infrared decoy to infrared imaging guidance anti-missile.Shipboard Electronic Countermeasure,vol.36,no.1,pp.43-46.

Zhang,X.Y.;Meng,W.H.;Fu,K.S.;Qi,M.(2008):Simulation model for countermeasure test of IR imaging missile.Infrared and Laser Engineering,vol.37,no.4,pp.569-572.

Zhao,F.Y.;Ma,C.X.;Lu,S.;Jiang,C.(2012):Development of the airborne IR decoy technology.Ship Electronic Engineering,vol.32,no.3,pp.20-22.

Zhong,Y.W.;Liu,J.R.;Yang,L.Y.;Shen,G.Z.(2008):Maneuver library integrated control system for autonomous close-in air combat.Acta Aeronautica ET Astronautica Sinica,vol.29,no.5,pp.114-121．

Zhou,Y.;Wang,Q.;Li,T.;Hu,H.Y.(2017):A numerical simulation method for aircraft infrared imaging.Infrared Physics ＆Technology,vol.83,pp.68-77.

Zou,T.;Wang,C.Z.;Tong,Z.X.;Jia,L.T.;Tong,Q.(2016):Diffusion rule of foilsurface-type infrared decoy.Acta Aeronautica ET Astronautica Sinica,vol.37,no.9,pp.2634-2645.