压力明钢管在日照温差作用下横向变形位移计算方法及对比分析

李润清

(山西省水利建筑工程局，山西 太原 030006)

压力明钢管是大中型电站的主要引水方式，通常在水电站一系列的支墩上敷设压力明钢管，并且镇墩往往设置在管道一定长度或转弯处，伸缩节一般靠近上游镇墩，且位于两个镇墩之间，而支墩形式通常为滑动式或滚动式制作[1- 4]。支墩上的压力明钢管和镇墩分别相当于多跨连续梁与固定端，在温度变化时因伸缩节的存在管道自身可沿轴向产生自由伸缩。实际工程及相关研究表明，压力明钢管在管道放空检修期或者施工期可在日照温差作用下沿横向产生较大的变形位移，因此可对各支座产生明显的横向推力。当管道及镇墩设计不当时，可直接造成支墩混凝土破坏、地脚螺旋剪断以及钢管支座脱落等问题[5]。据此，本文在详细分析了压力明钢管横向变形位移在日照温差作用下计算方法和理论的基础上，利用结构力学方法对比分析了3种不同方法的适用性与精确度，以期为提高支座横向变形计算的准确度提供参考和借鉴。

1 横向温差位移计算

压力钢管简化模型为横向温度自由位移计算的基础和前提，因此结合相关研究和有关资料可将压力明钢管简化为悬臂梁的结构形式。其中悬臂梁的固定端和自由端可分别假定为压力明钢管的下游端镇墩与上游伸缩节处，然后假定钢管横向变形不受支座垂直约束的作用影响，钢管变形满足平截面假定并且以直线变化规律作为钢管横向温度梯度的变化形式[6]。

1.1 推导方法

在温度作用下静定结构的位移推导公式如下：

(1)

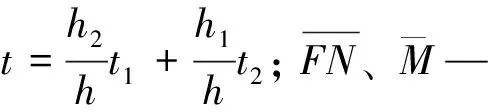
对于等截面杆件的温度位移，可采用下式进行求解：

(2)

(3)

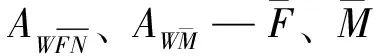
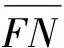
(4)

结合公式(3)、(4)可得到在温差作用下杆件的位移公式为：

(5)

式中，D、X—钢管直径和长度。

1.2 温变后圆弧明钢管轴线位移

在温度上升后，假定明钢管轴线变形为圆形，其轴线半径为R，则轴线变形后的方程可表示为：

R2=X2+Y2

(6)

式中，Y—X的钢管所对应的横向变形。

对温度位移，利用几何关系进行推导可得到两种方法分别如下：

(7)

考虑到αt0足够小，可假定为0，因此温差作用下轴线圆弧半径公式如下：

R=D/(αΔt)

(8)

利用上述结果和相关公式，可得到杆件在温度作用下的横向位移公式如下：

(9)

(2)先求角位移后，求轴线位移法。压力明钢管在温差Δt作用下引起的内外伸长量之差可采用公式Δl=XαΔt进行求解；然后对于圆心角为2θ的圆弧变形，利用几何关系可求得钢管阳面、阴面的圆弧长度，阳面相对于阴面的伸长量为Δl：

(10)

利用上述公式可实现弧度到角度的转化，并得到温度作用下压力明钢管的横向角位移，公式如下：

θ=90XαΔt/(πD)

(11)

考虑到温差作用下引起的角位移较小，因此可假定钢管变形前和变形后端点组成直角三角形，因此对钢管横向温度位移可利用几何关系进行求解，然后带入横向角位移公式可得到温度位移公式，如下所示：

(12)

2 压力明钢管日照温差下的横向变形计算

某工程压力管线爬山段采用压力明钢管，直径为1.6m，爬山段长度为0.3km，共40跨。自然条件下管道阳面和阴面温差为1℃，最大跨度10m。该工程采用涂塑复合钢管对传统的工艺防腐钢管进行优化，优化设计后管道壁厚16mm，优化后其主要优点如下：不仅可节省部分工程投资、降低防腐面积以及钢材用量，而且可有利于单节钢管的安装、吊装和运输，在一定程度上可提高施工速度、降低施工成本和后期运行费用。对涂塑复合钢管进行前处理，主要包括焊缝修模、喷砂除锈处理[7]。焊缝形状为圆弧状时，应保持板材与焊管内表面焊缝的圆滑过渡并避免出现死角、尖角以及直棱。对钢管内焊缝不符合有关要求时，应采用人工修磨方法进行修正处理，同时在进行钢管喷砂时应确保达到除锈和打出一定锚纹深度的粗糙度目标要求[8]。喷砂合格后，对钢管进行中频加热，外表面喷涂聚乙烯粉末，内表面喷涂环氧树脂粉末。

对压力明钢管各支墩处横向温度位移，分别利用上述3种不同方法进行求解，结果表明各方法结果保持良好的一致性。然后，与有关文献和资料中有限元模型对各支座横向温度位移的计算结果进行对比，各支座位移大致保持相等，同时二者具有较高的一致性与吻合度，其中在12号支墩处横向温度位移结果值最大。见表1。

研究表明，压力明钢管轴线变形在一定的日照温差下符合圆弧形基本假定。钢管直径D、长度X以及温差为3种不同计算方法中包含的主要参数，尽管不同计算方法的函数形式存在一定差异，但其计算结果保持相同。

进一步对后2种方法在实际工程中的适用性以及准确性进行分析可知，横向温度位移计算方法1为单位荷载法推导的基准和前提条件，因此后2种推导方法对钢管长度、温差、以及直径等参数的敏感性较高[9]，直径、温度和温差对横向温度位移的影响程度高于方法1。

表1 不同计算方法对钢管横向温度位移计算结果

在钢管直径为1.8m不变的条件下，分别对温差为20℃、15℃、10℃和5℃时最远端钢管温度变位进行计算，结果见表2。

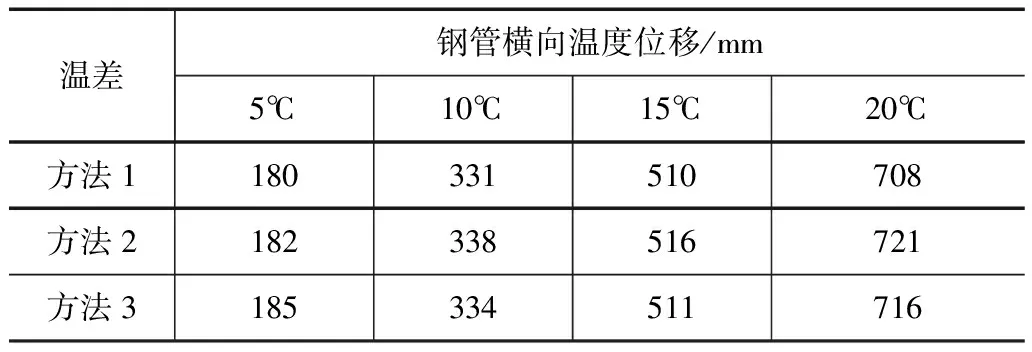
表2 不同温差条件下钢管横向温度位移

由表2可以看出，3种不同方法对不同温度条件下钢管横向温度位移的计算结果非常接近，其中后2种方法结果略高于方法1，并以方法2的横向温度位移值最大。通过对比不同问题条件下各计算方法的变化趋势可知，各计算结果的差值随温度的增大而逐渐提高，但是各方法在不同温度下的横向位移均符合实际工程精度要求。

在保持最大温差不变的条件下，分别选取钢管直径为5.0、4.0、3.0、2.0m进行自由温度变位计算，即保持20℃最大温差对不同钢管直径的最远端自由温度变位分别采用不同方法进行求解，结果见表3。

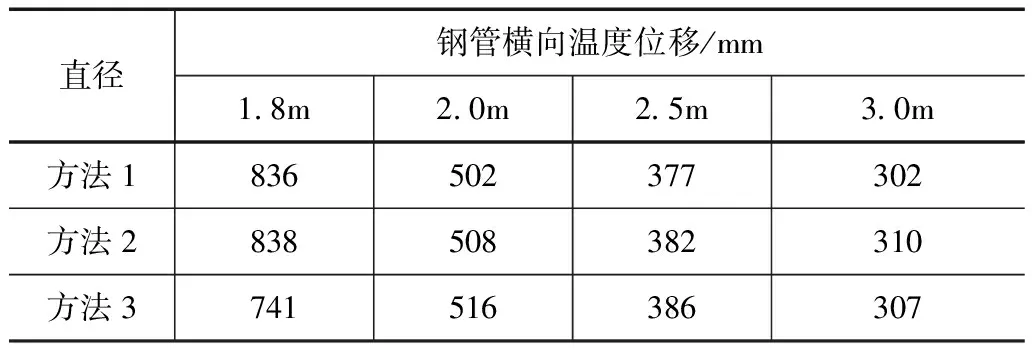
表3 不同直径条件下钢管横向温度位移

根据表3计算结果可知，在保持最大温差为20℃不变时，对不同钢管直径的横向温度位移利用不同方法进行求解，其结果具有良好的一致性；后两种方法的计算结果整体略高于方法1，并以方法2的计算结果值最大。研究表明，不同计算方法结果差值随钢管直径的降低而逐渐增大，即钢管直径越大则相应的温度位移差值越低。

保持钢管直径为1.8m，环境最大温差为20℃不变时，分别对钢管最远端距离为200、150、100、50m时的横向温度位移进行计算，结果见表4。

表4 最远端距离不同时钢管横向温度位移

由表4计算结果可知，在不同最远端距离条件下，各计算方法得到的钢管横向温度位移变化规律与前述温差、直径不同时的变化规律保持相同[10]，不同计算方法其结果大致保持相同；3种方法计算结果均表明差值随最远端距离的增大而增大，随最远端距离的降低而减少。

综上所述，在一定条件下对常规水电站压力明钢管温度变形假定为圆弧形具有合理性与可靠性，对不同横向温度位移的计算结果均符合实际工程的精度要求[11]。

3 结论

(1)通过不同的计算方法求解得出，压力明钢管在一定日照温度作用下其横向变形符合圆弧形基本假设，具有一定的合理性与准确性。对压力钢管的横向位移，不同方法的计算结果相差较小，且均符合实际工程精度要求。

(2)结构力学法即方法1推导求得的横向温度位移值略低于圆弧型轴线变形假定法；并且后2种方法随钢管直径的降低或温差、钢管长度增大，其计算结果相差值呈现出增大趋势。在一定条件下对常规水电站压力明钢管温度变形假定为圆弧形具有合理性与可靠性，不同横向温度位移的计算结果均符合实际工程的精度要求。研究成果可为提高压力明钢管在日照温差作用下的横向变形计算精度与准确性提供一定参考和依据。