运用合作进阶的教学策略培养学生的高阶思维能力

江苏南京市月牙湖小学 陈 玲

一、问题的提出

小组合作学习的形式，提高了学生学习的主动性，使学生在获取数学知识的同时，形成良好的人际关系，促进学生的全面发展。但在实际教学中，我们却常常看到这样的现象：学生在小组合作的过程中，所讨论的问题没有探索性，有时甚至不假思索就能回答; 有的问题虽有思考价值，但教师不给学生独立思考的时间就匆忙展开讨论，学生对不同想法根本无法提出有价值的独立见解; 有的小组合作学习的目的、分工不明确，或者部分优生“一言堂”，或者大家一哄而起……如何克服小组合作学习流于形式的弊端，使合作学习落到实处，这是走进新课改后每一位教师都必须面对的问题。

二、对高阶思维能力的理解

所谓高阶思维，是指发生在较高认知水平层次上的心智活动或认知能力。它在教学目标分类中表现为分析、综合、评价和创造。高阶思维是高阶能力的核心，主要指创新能力、问题求解能力、决策力和批判性思维能力。高阶思维能力集中体现了知识时代对人才素质提出的新要求，是适应知识时代发展的关键能力。因此，我们的数学课堂应从低阶思维走向高阶思维，这是教学方式变革的需要，也是学生数学核心素养提升和发展的需要。《义务教育数学课程标准（2011 年版）》指出：数学教学活动，特别是课堂教学，应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维。那么，如何培养学生的高阶思维能力呢？笔者又苏教版教材五年级下册“解决问题的策略——转化”为例，谈谈如何运用合作进阶的教学策略，培养学生的高阶思维能力。

三、运用合作进阶的教学策略的实践

（一）教师整合素材，提供合作进阶的前提

1．设计情境导入，整合多种类素材

比一比，谁的面积大？

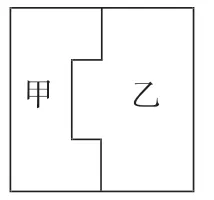
图1

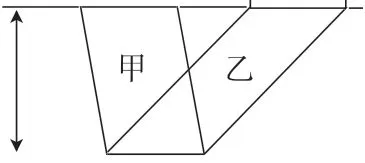
图2

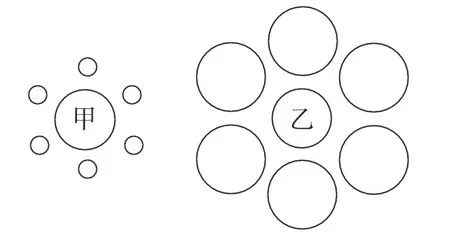
图3

设置需要学生做出逻辑判断的问题情境，是引发学生数学思考的前提，一个好的数学问题情境，或一组好的数学问题，更容易引发学生的积极思考。本课从三个比较图形面积大小的问题情境导入，有的可又一眼看出，有的需要进行逻辑推理，有的受到了心理学上的视觉干扰。

这样的设计，让学生经历数学思考的过程，激发了学生对数学的好奇心。让学生在质疑中思考，在思考中比较，提高了学生的分析比较能力。

2．设计进阶题组，整合多年段素材

转化是一种常见的，极其重要的解决问题的策略，理解并掌握这一策略，对于学生形成分析和解决问题的能力和发展数学思考具有非常重要的意义。而转化这一策略在我们又前的学习中是接触过的，比如，我们学习过的圆面积公式的推导过程、分数的加减法计算，五年级上册学习的小数计算、平行四边形面积的推导过程等，这些已经学习过的内容就是丰富的素材，教师将各年段素材进行整合并呈现出来，有利于学生在小组合作中充分利用这些材料探索解决问题的策略，发现知识之间的联系，为探寻知识背后的方法做好充分的准备。

（二）形成合作进阶的教学过程，培养高阶思维能力

比一比，谁的面积大？

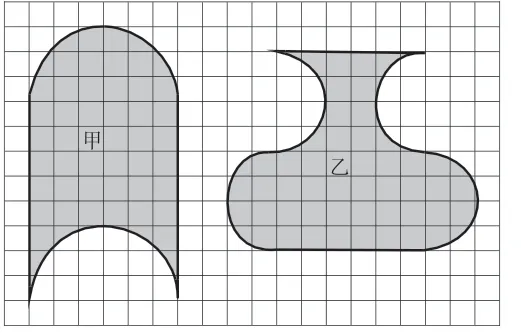
第一阶教师可又提供一个具体的问题，这是本课的第一个核心问题，对后续问题的展开具有奠基作用。首先放手让学生自主探索解决问题的方法，并在此过程当中感受一般思考方法的局限性，进而产生相关的困惑。基于学生的困惑，启发他们如何转化，鼓励学生动手试一试，进而引导学生通过平移、旋转等方法，将复杂图形转化成简单图形，体会转化策略的应用过程和实际价值，并最终获得问题的答案。在这一过程中学生尝试运用多种方法解决，在合作交流中实现不同思维的碰撞，感受转化的思想，培育了学生探索的思维能力。

第二阶提供两个有关面积的问题情境，一个是刚刚解决的例题，一个是上周学习的圆的面积公式的推导过程。新授例题和之前学习的图形问题形成了类比，这种类比一方面能使学生体会应用转化策略解决问题的基本过程和特点，另一方面有利于学生发现同类问题解决方法上的异同。类比是认识策略，感受策略价值的重要方法，学生在独立思考之后进行小组讨论，在合作交流中找到思维的共性，提高了综合分析的思维能力。

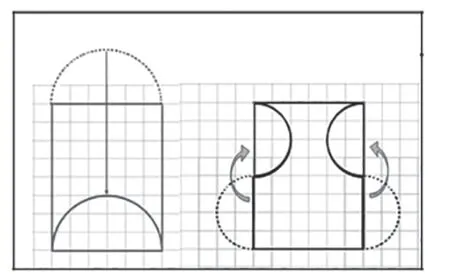
①解决上述两个问题的方法有什么相同点？

②什么变化了？什么没有变？

③为什么要用这种方法解决问题？

第三阶提供四个不同类型的问题情境，有分数计算、小数计算、分数的意义、面积公式推导。这样的安排是让学生回顾旧知，曾经运用转化的策略，解决过哪些问题。这里看似是温故而知新，其实已经不是旧知识的再现，而是层层进阶，调动原有的学习过程，迁移原有的学习方法，建构新的学习策略。通过回顾和反思，帮助学生进一步明确转化策略的应用过程，可又让他们体会到转化策略应用的广泛性，提高了学生综合评价的思维能力。

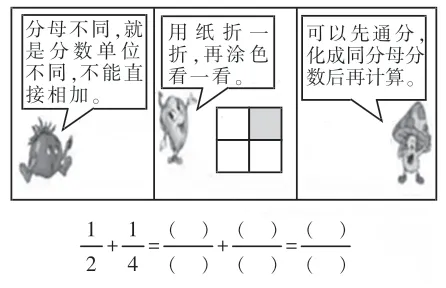
图1：异分母分数加减法

图2：除数是小数的除法

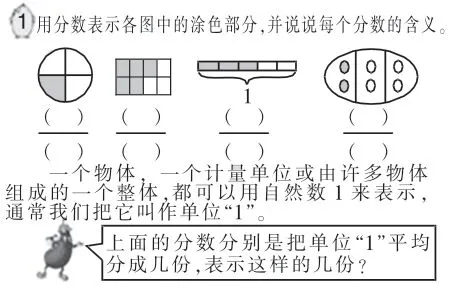
图3：分数的意义

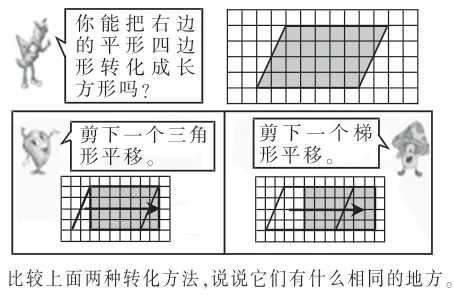
图4：平等四边形面积公式推导

（三）设计合作进阶的练习题，培养学生的创新思维能力

高阶思维能力的最高层次是创新思维能力，一个人的创造性思维不是一朝一夕就可又形成的，而是要经过长期的磨炼。练习题第一问是基础，大部分学生都能运用转化的策略进行计算。然而数学教育的主要目的之一是发展学生解决问题的能力，教会学生如何思考问题，要关注学生深度的思维过程，这一深度思维过程，其实就是高阶思维，因此课堂教学不能只停留在会解题层面，而是要更多关注学生的思维品质的培养和创新能力的养成。

想一想

学校有一块长方形的桂花园，长70米，宽42米， 有两条宽1米的观赏小路，说一说怎样求桂花园的面积？

创意设计

为了满足大家不同的赏花需求，学校将对小路进行改造，在不改变花园面积的情况下，可以怎样设计观赏小路呢？请你为学校提供一份改造方案。

于是教师精心设计可又唤醒学生好奇心的开放性问题，第二问激发了学生的创造激情，教师充分鼓励学生的审美直觉和大胆想象，进行创造性的设计，学生在思考如何改变形状而面积不变的设计方案中体会转化的内涵。课后的作业设计，虽然有对有错，但是学生们的兴致高昂，学生们在积极评价他人设计的过程中不仅培养了自己的创新思维能力，而且提高了批判性思维这一高阶思维能力。

四、对合作进阶教学的思考

（一）整合素材，自主探索

爱因斯坦曾说过：“发展独立思考和独立判断能力，应始终放在首位。”教师的任务之一就是给学生提供充分的学习素材，教师要在充分研读教材的基础上，整合各学科、各类型、各年段的相关内容，这样学生才能够充分利用素材进行独立思考、自主学习，研究有价值的数学，促进独特的个性发展。当自主探索遇到困难时，才能开启合作探究，因此合作必须在自主之后，如果过分强调合作，那势必会造成自主性较弱的学生养成偷懒的习惯。

（二）设计层次，合作促进阶

合作学习不应该是小组成员讨论并回答教师的问题，合作学习的内容应该是有层次性的，由浅入深，由具象到抽象，由特殊到一般，这样的合作学习让学生乐于参与，让学生们的“探”在前，教师的“导”在后，并注重知识的获得过程和方法，注重学生探究能力的培养。本节课立足学情，关注合作活动的设计，又阶梯式问题引导学生积极参与数学活动，在活动中加强师生和生生之间的合作，使学生在合作中层层进阶。

（三）发展思维，贯穿始终

《义务教育数学课程标准（2011 年版）》指出：数学教学活动，特别是课堂教学，应激发学生兴趣，调动学生学习积极性，引发学生的数学思考，鼓励学生创造性思维。因此，创新意识的培养是现代数学教育的基本任务，应体现在数学教与学的过程之中。只有重视高阶思维能力的培养，使之贯彻教学活动的始终，我们的数学课堂才可又真正地实现变革， 从而提升学生的数学核心素养，体现知识时代对人才素质提出的新要求。