基于上限分析的边坡稳定性评估

何 阳, 徐定芳

(湖南省地质调查院，湖南 长沙 410116)

1 引言

边坡稳定性分析一直是岩土工程领域重要的研究课题之一。目前实际工程中最常使用的是极限平衡理论，基于刚极限平衡理论的各类条分法计算简便、发展相对完善，并在实际中取得了大量经验，在工程中应用较为广泛。但该类方法的弊端也是显而易见的，即无法考虑边坡破坏的运动学问题，因此在稳定性分析中不可避免的存在误差。

极限分析上限法能够不受结构几何形状及荷载情况复杂程度的制约，利用所选取的机动许可速度场可直接求得到一个实用的荷载值，并且还能够提供一个清晰的破坏模式的物理图形，近年来获得了广泛研究与应用。Chen最先将上限分析法应用到岩土工程领域，并利用该方法解决了边坡临界高度问题；王敬林等讨论了上限法涉及的关联流动法则、体积剪胀变形、摩擦功等问题，提出一种基于广义塑性力学的极限分析上限法；张小艳等基于上限分析条件，建立一种边坡可靠度分析上限法随机规划模型，对边坡进行风险性评估。

上限分析主要是基于塑性力学，构建满足运动许可的应力场，只考虑速度模式和能量消耗，而不考虑材料的本构关系，过程更为简单、直接。本文以塑性极限分析上限法为基础，构建边坡临界高度上限解计算模型，为边坡的稳定性评估提供一个可选路径。

2 上限分析基本模型

上限分析主要内容的是速度模式(或破坏模型)和能量消耗，首先建立边坡稳定性分析机构，假定破坏面通过坡趾，如图1所示。

其破坏机构的对数螺旋方程为：

r=r0exp[(θ-θ0)tanφ]

(1)

三角形坡体区ABC绕旋转中心O点做旋转运动，OB、OC的倾角分别为θ0和θh，由几何关系可以推导出H/r0和L/r0：

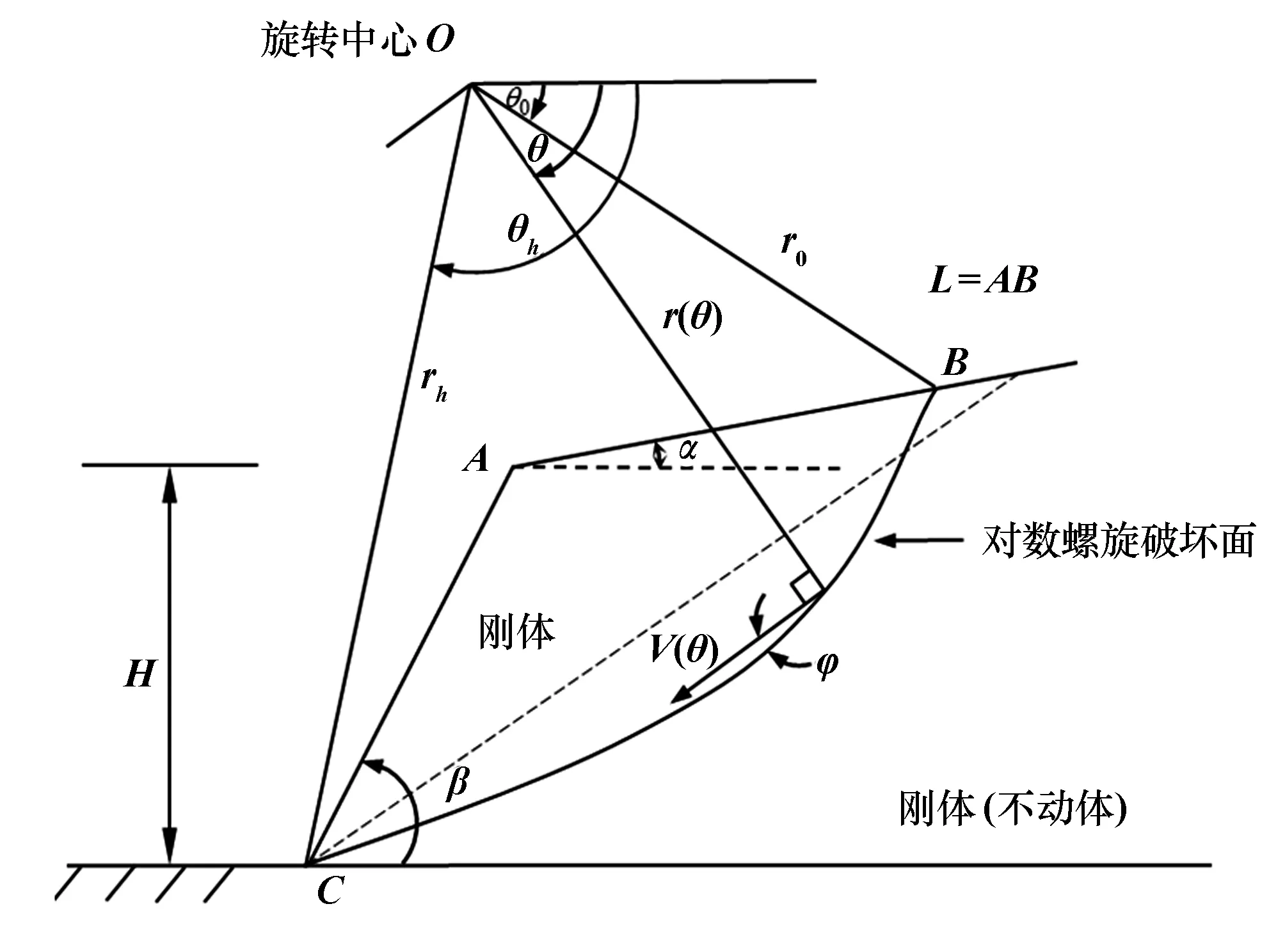
图1 均质边坡破坏机构(破坏面通过坡趾)

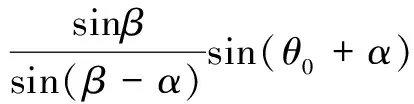
(2)

{exp[(θh-θ0)tanφ]sin(θh+α)-sin(θ0+α)}

(3)

则ABC区由土重所做的功率为：

WABC=γr03Ω(f1-f2-f3)

(4)

式中，γ为土体容重，Ω为ABC角速度；函数f1(θh,θ0)、f2(θh,θ0)、f3(θh,θ0)分别定义为：

exp[3(θh-θ0)tanφ]-(3tanφcosθ0+sinθ0)}

(5)

(6)

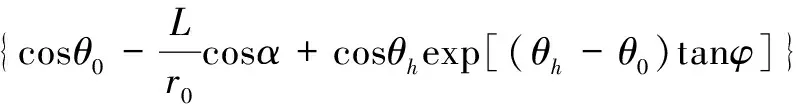
(7)

内部能量损耗主要发生在间断面BC上，沿整个间断面积分即可以得到总的内部能量耗损率：

(8)

令外功率即式(4)与内部损耗率即式(8)相等可得：

(9)

式中f(θh,θ0)定义为：

{sin(θh+α)exp[(θh-θ0)tanφ]-sin(θ0+α)}

(10)

当f(θh,θ0)中当θh和θ0满足条件：

(11)

函数f(θh,θ0)具有一个最小值，因此解出这些方程，并把所有θh和θ0带入式到式(9)，即可得到边坡临界高度的一个最小上限解。

3 工程实例

拟评估边坡位于常德市武陵区白鹤山乡东侧，边坡区域整体较为平坦，由东向西缓倾，地震设防烈度为Ⅶ度，为均质土质边坡。边坡前缘为修筑的乡村道路，后缘存在明显岩土交界面，纵向长约160 m，横向宽约90 m，坡高约60 m。随着修路对边坡坡脚处开挖，造成坡体部分部位出现明显裂痕，严重影响坡体下方居民及道路行人安全，如图2所示。

图2 边坡整体概况

根据现场勘查及钻探取样，可获得边坡中心点处剖面图如图3。边坡土体基本物理力学性质指标如表1。

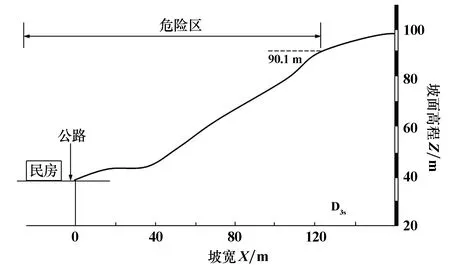
图3 边坡剖面图

参数最大值最小值均值c/kPa24.821.823.12φ/(°)18.615.317.08γ/(kN·m-3)19.318.018.9

利用本章方法对边坡的整体稳定性进行评估，假定边坡破坏面通过坡趾，带入以上各式可得边坡临界高度Hc = 48.52 m，可以看出，边坡实际高度H = 60 m>边坡临界高度Hc，因此，可判定出该边坡整体上处于不稳定状态，需要尽快对其进行稳定性加固或削坡处理等。

4 结论

文章基于塑性极限分析上限法，建立满足运动要求的速度场，利用所构建出的边坡破坏机构，在破坏面通过坡趾条件下，以外功率等于内部损耗率为控制条件，获得了边坡失稳临界高度的一个上限解。结合实际工程算例，对边坡整体稳定性进行了评估，展示了本文方法的实用性。