基座弹性的双柔杆空间机器人的神经网络动态面控制

黄小琴，陈 力*

(1. 福州大学，机械工程及自动化学院，福州 350116； 2. 福建省高端装备制造协同创新中心，福州 350116)

1 引言

空间机器人能够辅助航天员完成太空任务，可大幅度提高人类探索太空的工作效率[1-2]。空间机器人的臂杆因具有长臂，重载等的特点，往往都存在柔性；而空间机器人沿着由桁架组装的导轨移动，在这工作操作过程中会激发导轨的振动，带动基座产生弹性振动，由于基座与臂杆存在耦合关系，造成跟踪轨迹偏差[3-4]。因此对空间机器人控制的研究须考虑臂杆柔性与基座弹性振动的抑制问题。于潇雁等[5]采用自适应控制方法实现了多柔杆空间机器人的轨迹跟踪的同时，应用最优控制进行柔性抑振。梁捷等[6]针对基座弹性影响，采用级联控制法抑制了柔性关节空间机器人的基座与关节振动，但未考虑臂杆的柔性振动。Park等[7]应用反演法，设计了机械手的模糊神经网络方法。以往的研究将臂杆柔性和基座弹性均考虑在内的空间机器人研究较少。

动态面是Swaroop等提出的一种空间机器人动力学控制的有效方法[8]，通过设计一阶低通滤波器估计虚拟控制部分，解决了反演法中在后退过程中，虚拟控制部分重复求导出现的“微分爆炸”问题。Cheong等[9]结合模糊逻辑系统，设计了刚性机器人的状态观测器、参数估计器及动态面滑模控制方法。

本文综合考虑空间机器人两臂杆的柔性和基座的弹性，基于奇异摄动理论，将系统分解为快、慢变子系统：针对慢变子系统设计一种动态面控制器，以避免反演法的计算膨胀；以RBF神经网络逼近包含外部干扰在内的动力学不确定项，从而使基座与两关节铰跟踪期望轨迹。对于快变子系统，采用线性二次型最优控制抑制弹性基座与两柔杆的振动。

2 系统动力学模型

以基座、臂杆全弹性空间机器人为被控对象，系统可简化为如图1所示的由自由飘浮的基座B0加柔性臂杆B1、B2。将导轨弹性简化为一个轻质弹簧，以表示基座的弹性，χ为弹性位移，并可以假定：

1) 弹簧为无质量弹簧；

2) 弹簧只做沿着轴线的拉缩运动；

3) 弹簧的弹性系数kχ为常量；

4) 弹簧初始位移为零。

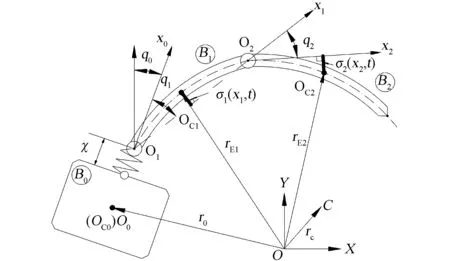
图1 基座、臂杆全弹性空间机器人系统Fig.1 Space robot system with flexible links and elastic base

建立各分体Bi(i=0,1,2)的联体坐标Oixiyi，其中O0与B0的质心Oc0重合，Oi(i=1,2)分别为相应的转动铰中心。B1杆的转动铰O1与B0之间用轻质弹簧连接，x0轴通过O0与O1的连线，x1轴与O1O2在同一直线上，x2轴与B2始终相切于O2。在初始状态下，O1在x0轴上与O0的距离为l0，Bi(i=1,2)沿xi轴的长度为li；载体的质量与绕质心的转动惯量分别为m0、J0。C为系统的总质心。以空间任意点O为原点，设立平动惯性坐标系(O-xy)。

考虑两臂杆均为细长匀质杆件，可只考虑其弯曲变形，忽略其轴线与剪切变形，同时两臂杆在平面内作横向振动。柔性臂Bi(i=1,2)的线密度为ρi，截面抗弯刚度为(EI)i。根据振动力学理论[10]，这两柔性臂可视为伯努利-欧拉梁，那么其弹性变形记作式(1)：

(1)

其中，σi(xi,t)为Bi在截面xi(0≤xi≤li)处的横向弹性变形，ωij(xi)为Bi的第j阶的模态函数，ξij(t)为与ωij(xi)对应的模态坐标，ni为截断项数，大幅值的振动主要由前几阶模态构成，取ni=2。根据文献[10]可查询到相对应的模态函数。利用拉格朗日第二类方程，可得基座弹性的双柔杆空间机器人的动力学方程如式(2):

(2)

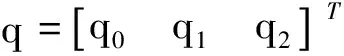
3 快、慢变子系统分解

运用奇异摄动方法，将动力学系统分解为快、慢变子系统，为此，将式(2)表示成式(3)所示分块矩阵形式：

(3)

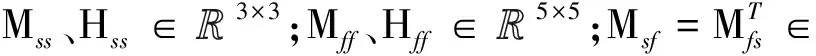
(4)

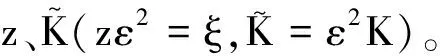
(5)

设计如式(6)所示组合控制律：

τ=τs+τf

(6)

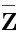
(7)

其中，矩阵或变量上加上划线“-”意为与之对应的慢变分量。将上式代入式(6)，得到慢变子系统如式(8)：

(8)

(9)

4 慢变子系统控制器

4.1 控制器设计

考虑外部干扰τd，慢变子系统可写为式(10)：

(10)

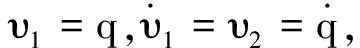
(11)

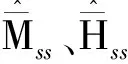
采用动态面控制方法设计虚拟控制量和控制输入信号，在此基础上设计τs。动态面控制的设计步骤如下：

1)定义第一个误差面如式(12)：

s1=e=υ1-qd

(12)

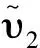
(13)

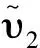
(14)

其中，时间η2>0。定义慢变子系统边界层误差如式(15)：

(15)

求υ2d的一阶导数，得到式(16)：

(16)

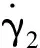
(17)

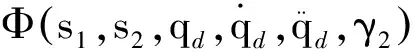
2)提出第二个动态面s2如式(18)，进而设计τs：

s2=υ2-υ2d

(18)

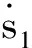
(19)

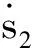
(20)

利用RBF神经网络来逼近Θ(X)=TΔ。记Θ(X|W)为Θ(X)的一个逼近，如式(21)

Θ(X|W)=WTO(X)

(21)

其中，W为权值矩阵，O(X)=[O1,…,Oh]T为基向量，h为基函数列向量。输入X=[X1,…,Xm]T，m为基函数中心点个数；O(X)的元素为式(22)所示高斯基函数：

(22)

其中，aj、bj分别为曲线的中心、宽度。W的最优值W*是一个常数矩阵且满足式(23)：

(23)

其中：ΩW={W|‖W‖≤ρW}，ρW为有界正常数。则Θ(X)可表示为如式(24)所示：

Θ(X)=W*TO(X)+μ*

(24)

其中，μ*为最优逼近误差。设计慢变子系统的控制规律为式(25)：

(25)

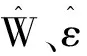
(26)

(27)

其中，β1∈h×h，β2∈3×3。λ1>0，λ2>0。由控制规律式(25)，求出如式(28)：

(28)

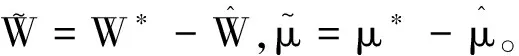
4.2 稳定性分析

定理：对于空间机器人慢变子系统，控制规律式(25)将使系统半全局最终一致有界，即e收敛到零的一个任意小邻域内。

证明：构造如式(29)所示的李雅普诺夫函数V：

(29)

其中，V满足初始条件V(0)≤ρV(ρV为正实数)。求V关于时间t的一阶导数如式(30)：

(30)

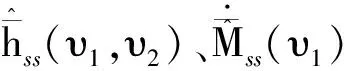
(31)

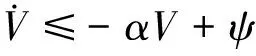
(32)

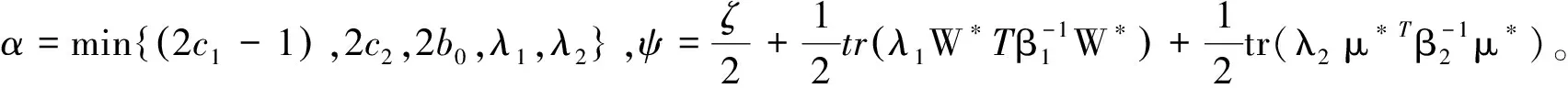
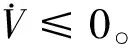
0≤V≤ψ/α+[V(0)-ψ/α]e-αt

(33)

上式表明V最终以ψ/α为界。因此系统半全局最终一致有界，即e收敛到零的一个任意小邻域。

5 快变子系统的线性二次控制器

本文采用线性二次型调节器来控制系统的快变子系统，以抑制弹性基座与两柔杆的振动。

(34)

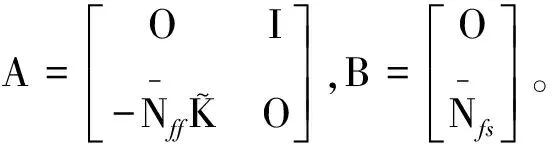
利用最优控制方法可将系统状态变量P调节到零，从而实现基座弹性与两杆柔性振动的抑制。引入如式(35)所示形式的线性二次最优控制性能指标函数：

(35)

其中，Q∈10×10为半正定加权对称阵，R∈3×3为正定加权对称阵。

为了最小化Υ，控制量应设计如式(36)：

τf=-R-1BTΞP

(36)

其中，Ξ满足式(37)所示的Riccati代数方程：

ΞA+ATΞ-ΞBR-1BTΞ+Q=O

(37)

6 仿真验证

以图1所示的模型为例，在MATLAB中进行数值仿真实验。系统惯性与结构参数取值为：l0=l1=1.5 m,l2=1.0 m,m0=40 kg，J0=34.17 kg·m2，ρ1=3.5 kg/m，ρ2=1.1 kg/m，(EI)1=50 N·m2,(EI)2=50 N·m2。弹簧刚度系数kχ=500 N/m。τd(t)取值为:τ0 d=2.5[cos(πt/6)-sin(πt/6)]，τ1 d=2.5cos(πt/6)，τ2 d=2.5sin (πt/6)。设qd分别为：q0d=π/6 rad，q1d=-π/2 rad，q2d=-π/6 rad。初始位形分别取为：q0(0)=0.1 rad，q1(0)=(π/3-0.2) rad,q2(0)=(-π/6-0.15) rad。基座弹簧初始位移为χ(0)=0。设定轨迹追踪过程仿真时间为t=30 s。

图2为基座弹性的双柔杆空间机器人采用文中控制方案时q的实际轨迹与期望轨迹。约12 s之后，基座，关节1和2的稳态误差分别在2×10-4rad、1×10-3rad、8×10-4rad以内。图3为该控制方案下基座弹性振动情况。弹性位移在0.05 s时从最大的0.0678 m到15 s后衰减为零。图4、图5为两柔性臂杆一、二阶模态情况。B1杆一阶模态从2.0 s时最大的0.0643 m衰减到零，二阶模态从0.2 s的0.0075 m衰减到零；B2杆一阶模态从0.8 s的0.0337 m衰减到零，二阶模态从0.02 s的0.0085 m衰减到零。从仿真结果可以看出：q能很好地跟踪上期望轨迹，同时抑制了基座弹性与两柔杆的振动。

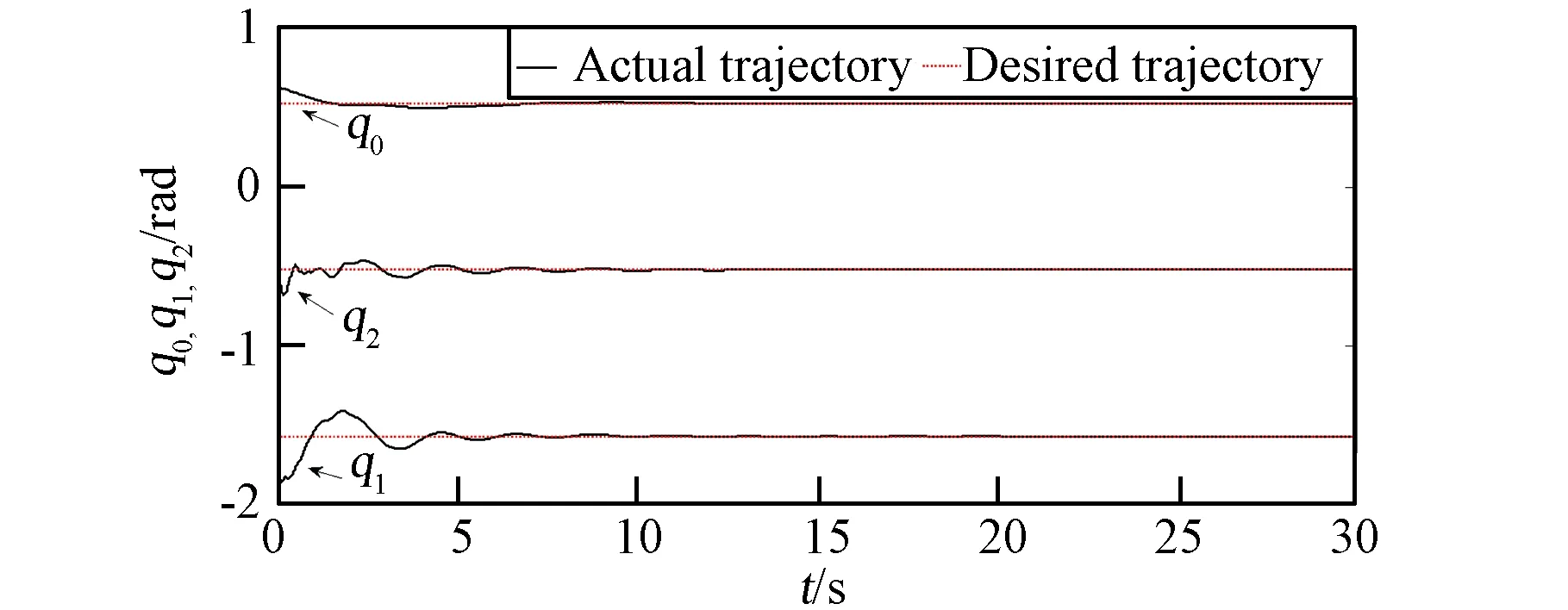
图2 基座与两关节铰姿态角的轨迹图Fig.2 Trajectory tracking of the base‘s attitude and the two links’ joints

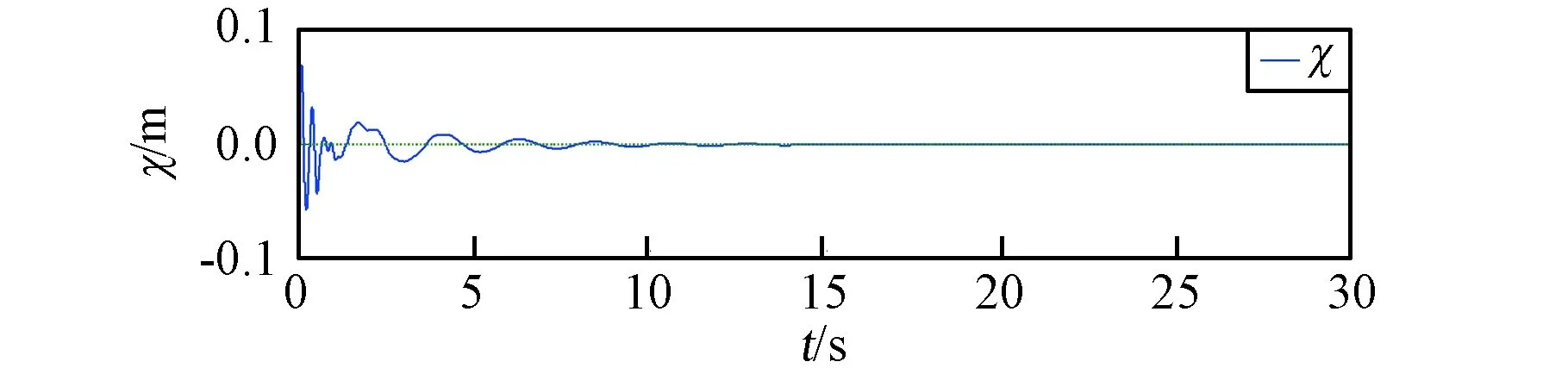
图3 基座弹性位移图Fig.3 Elastic displacement of the base

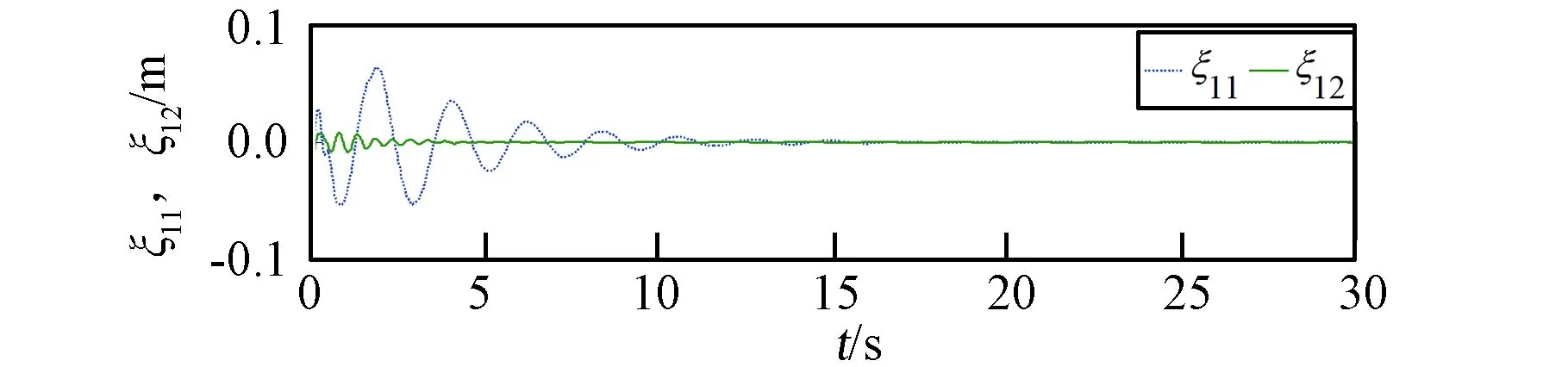
图4 柔性杆B1的模态Fig.4 The mode of flexible linkB1

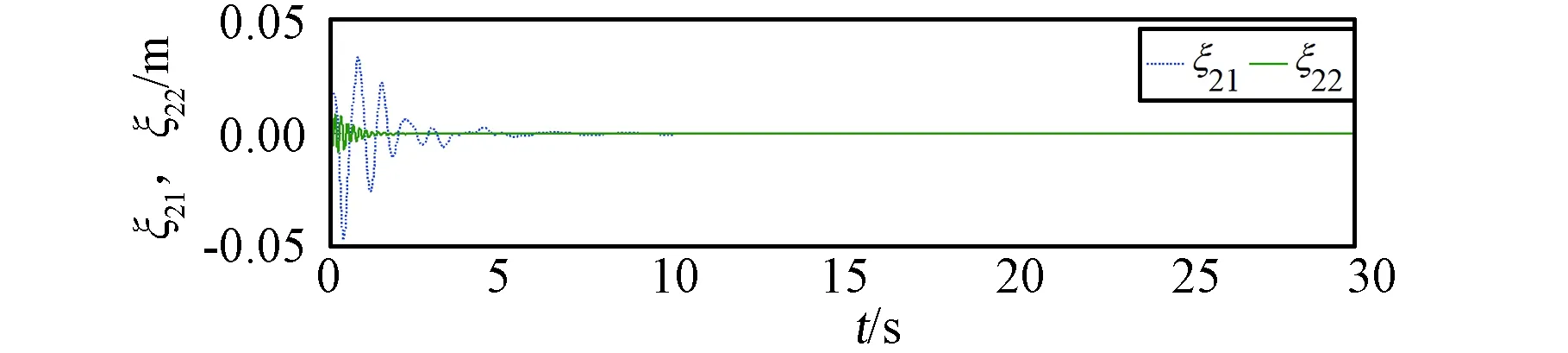
图5 柔性杆B2的模态Fig.5 The mode of flexible linkB2

7 结论

针对基座弹性的双柔杆空间机器人系统，仿真实验验证了所提神经网络动态面控制方案的有效性和可行性。控制器能有效的补偿外部干扰和模型不确定性，具有良好的轨迹跟踪和振动抑制性能。

空间机器人是多自由度的三维臂杆结构，本研究探讨的对象虽为二维空间机械臂系统，但本文所提控制方案经适当扩充，可以推广并应用于太空中从事空间活动的一般三维空间机器人系统。