黏性土的颗粒数量对PFC2D数值模拟影响的研究

刘姗姗 闫倩倩

(聊城大学东昌学院，山东 聊城 252000)

土体是离散的颗粒，离散元理论比有限元更能描述土体的性质。颗粒流程序PFC2D以此为理论基础进行编程，模拟土体颗粒的基本单元采用刚性圆球或圆盘，该基本单元综合考虑了土体颗粒的运动和相互作用，以期最大可能的接近实际问题。

在数值模拟过程中，颗粒数量的多少直接影响软件的计算速度与精度。若颗粒数量过少，则模拟结果误差较大，难以反映实际土体的接触特性；虽然颗粒数量越多，模拟结果越精确，但会影响计算速度，甚至导致计算中断。因此，选取合适的颗粒数目对数值模拟也是至关重要的。以黏性土材料为例，利用PFC2D模拟其单轴压缩试验。

1 参数设置

在颗粒流PFC2D模型中，颗粒间默认是没有黏结的，黏性土之间的黏结模型可通过软件中的接触黏结模型和平行黏结模型建立。两种黏结模型需同时存在，并只在颗粒间适用，而墙体和颗粒间是不能设定黏结的。其中接触黏结模型描述的是小范围内的黏结，类似于点接触，只能传递力；而平行黏结模型可传递力和弯矩，这主要是由颗粒间设定的具有截面形状和尺寸的黏结材料决定的[3]。该模型需要设置的参数有很多，为考察颗粒数量对数值模拟的影响，因此只通过土体颗粒半径改变模型内颗粒数量，而其他参数保持不变，如模型尺寸、平行黏结刚度、平行黏结强度等细观参数。数值模拟计算中，参数的设置关系到能否真实反映原结构力学和运动学的特征。数值试验中墙体的生成采用“wall”命令，“墙单元”是用来生成模型边界条件，在墙单元上不能直接施加力的边界条件，只能通过施加速度间接达到颗粒集合的位移和力的边界。颗粒与墙体间的摩擦对计算结果影响较大，可以通过设置颗粒—颗粒之间的摩擦系数等于墙体—颗粒之间的摩擦系数，降低该影响。通过增加刚度实现对压盘材料刚性加载的目的。通过减小约束墙体刚度，能够降低墙体的边界效应对计算结果的影响，实现约束墙体与颗粒间的柔性约束接触。但墙体刚度越小，两者之间的柔性接触则会越柔软，当超过极限值，墙体会被颗粒穿过流散出去。经过许多数值试验的验证，最终得到墙体刚度缩放系数合理的选择范围，即约束的墙体或施加的外围压是颗粒刚度的0.1倍左右，而加载压盘刚度为颗粒刚度的10倍左右[8]。在PFC2D模型中，主要的控制参数见表1，且墙体的法向刚度为3×109Pa。

表1 黏性土试件细观参数

2 模型建立

如图1是适当的墙体刚度和颗粒刚度比值下生成的颗粒模型，其中黏性土模型的孔隙率为0.1，模型尺寸为100 mm×50 mm。

单轴抗压试验是在“样品”两侧不设约束，直接由上加载板以一定的加载速度移动，同时控制下加载板的移动速率为0，直至样品破坏，如图2所示为颗粒数量为1 674的黏性土试件破坏形态，此时颗粒半径为0.5 mm～1.35 mm。按照文献[5]中所述的数值“样品”生成及位移和力的边界条件的模拟步骤可实现单轴抗压试验模拟。

3 模拟结果分析

通过PFC2D模拟运算，图3表示该试件最终破裂时的位移矢量状态，箭头表示颗粒的位移方向，箭头方向即为颗粒移动方向，而位移的大小与箭头的长度成正比。当颗粒有整体较大的位移时将产生箭头密集区域，反之，则会出现箭头稀疏区域。图3a)为模型整体，图3b)为图3a)中框内区域放大图。

为了与室内黏性土试件单轴压缩试验曲线相匹配，使数值试验结果与实际物理模型试验结果相一致，则需要进行一系列的PFC模型的细观参数输入，用来记录轴向荷载、轴向位移、裂隙数量的变化。根据PFC2D步长与荷载曲线、步长与位移曲线，可以得到图4黏性土试件数值模拟的荷载—位移曲线图。

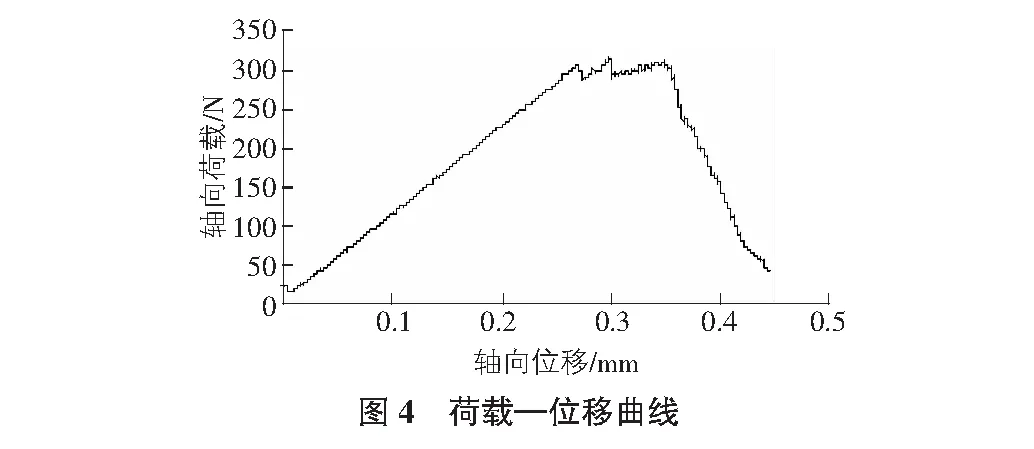
根据以上荷载—位移曲线图，黏性土试件轴向位移达到0.3 mm时产生变形破坏，此时黏性土的极限承载力314 N。

在试件达到极限承载力，破坏时产生裂隙，图5为黏性土试件裂隙数量与轴向位移曲线图。

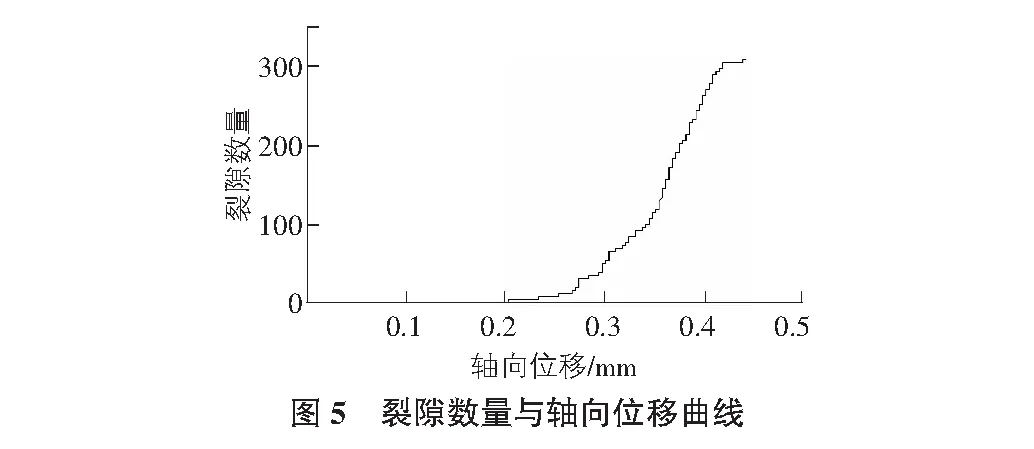
改变模型内颗粒半径，从而改变模型内的颗粒数量，利用PFC重复上述试验，对黏性土进行单轴压缩试验，得到各荷载—位移曲线，发现所有荷载—位移曲线均如图4所示出现峰值，从而得到轴向荷载峰值，在峰值时黏性土发生变形破坏，且试件的裂隙数量与轴向位移曲线均如图5所示，最后趋于稳定。

本试验中颗粒数量取值分别为：1 674，2 104，2 725，3 390，3 666，4 735，5 169，5 729，7 073，11 693，15 915，35 809。其中颗粒数量过多，影响运算速率，此时颗粒半径为0.1 mm～0.3 mm，故需要选取最合适颗粒数量的模型，采用比较各个模型中黏性土单轴抗压强度的方式，以此得到最合适颗粒数量及相应半径。

单轴抗压强度的计算采用如下公式：

其中，Rc为试件的抗压强度，MPa；P为试件破坏时的最大荷载，N；d为试件直径，mm。

单轴抗压强度—颗粒数量曲线如图6所示。

由图6可知，当颗粒数目大于3 000左右时，土体的单轴抗压强度基本保持稳定，此时颗粒半径为0.5 mm～0.8 mm。

4 结语

本文主要通过利用PFC2D颗粒流对黏性土进行单轴压缩试验，“样品”尺寸为100 mm×50 mm，规定其他参数不变，改变颗粒半径，获得此时对应的模型内颗粒数量，当颗粒数量小于3 000时，其单轴压缩强度浮动很大，与颗粒数量之间并没有线性或特殊函数关系。当颗粒数量大于约3 000时，颗粒半径为0.5 mm～0.8 mm，其单轴压缩强度基本保持稳定，即颗粒数量对整个PFC模拟的结果影响很小，可以忽略。