扰动粗粒土修正Duncan-Chang模型建立方法及应用

黄剑兵 陈 娟 刘力琦

(中国建筑东北设计研究院，辽宁 沈阳 110003)

0 引言

粗颗粒土为常见的土体材料，极易就地取材，可减少岩土工程成本。但由于其各向异性、受扰动影响强烈等工程特性，也极易在工程设计中影响计算结果及计算精度，造成工程事故或设计过于保守。在现有的土体分析中，由于参数意义明确且试验相对简便[1]，邓肯—张模型(D-C模型)在实际应用中仍旧占有主导性作用，因此就目前而言，对于粗颗粒土的分析大部分仍基于传统的邓肯—张模型，但较细颗粒土而言，D-C模型在粗颗粒土应力—应变关系的预测中精度大大降低且结果偏于不安全，尤其是在易扰动的粗颗粒土的施工扰动过程模拟及破坏模拟中其劣势体现得尤为明显[2]。因此，本文依托传统D-C模型，结合新型扰动状态函数，提出基于不同扰动状态的粗颗粒土非线性弹性本构模型，对扰动状态下的粗颗粒土的力学行为进行更精准预测，以期为今后的研究及工程应用提供理论依据。

1 土样大三轴剪切过程简介

试验选取中国东北地区三种常见粗颗粒土(圆砾、中粗砂及砾砂)，进行常规土工试验，对上述粗颗粒土进行定性分析，确定试样直径、加载速率及饱和判定等试验相关参数，以使试验过程规范化和便捷化，获得的修正模型相关数据合理化，上述粗颗粒土土性参数详见表1。

对试样进行大三轴固结排水剪切试验(以下称CD试验)前，先对试样进行反压饱和，在CD试验过程中，本文选取的控制应变率为0.015 mm/min。试验终止条件为试样的轴向应变达到15%。

表1 土性参数表

2 修正非线弹性本构的建立

2.1 确定扰动性函数

DESAI[3]首先提出了扰动状态概念(DSC)，采用扰动度(DD)度量材料受扰动的程度，认为一般材料均为相对完整(DD=0)和完全调整状态(DD=1)的混合体。扰动可能会使土体力学指标弱化，也可能会使其强化，所以扰动可区分为负面扰动和正面扰动[4]。

施工过程中，土体受到扰动程度与土体密度、含水量、不均匀系数、相对密实度等土性参数有关。而在土体扰动过程中，相对密实度Dr的变化较其他参数尤其明显[4]。据此，本文基于DSC理论，参考正/负扰动概念，以Dr为媒介，提出了能全面考虑粗颗粒土体正/负面扰动影响的统一扰动度函数：

(1)

其中，Dr0为粗颗粒土初始相对密实度；Drmax,Drmin分别为最大/最小相对密实度。

2.2 考虑扰动影响的修正D-C模型

为将统一扰动度函数引入传统D-C模型中，提出考虑扰动影响的粗颗粒土非线弹性本构模型的构建方法，本文针对我国北方地区三种常见粗颗粒土，分别对其扰动试样进行不同相对密实度条件下的CD试验。结果表明：以Dr为载体进行考虑扰动影响的D-C模型修正过程中，Dr的变化会对原始模型中的参数K及峰值强度产生巨大影响，而对于模型中的其他试验参数影响微小，因此，扰动本构模型修正方法可仅对此二参数进行修正。

以Dr和破坏比为媒介，建立了扰动度DD—初始切线模量Ei关系曲线和扰动度DD—极限偏应力差(σ1-σ3)ult关系曲线，将统一扰动度函数引入至D-C模型中，提出考虑扰动的粗颗粒土修正D-C本构模型的构建方法如下：

1)对粗颗粒土试样进行不同Dr条件下的CD试验，得到粗颗粒土试样的轴向应变、径向应变随应力的变化，计算粗颗粒土试样的体积应变；

2)绘制偏应力—轴向应变、体积应变—轴向应变关系曲线，得到不同围压条件下的峰值应力，计算得到不同围压条件下的极限偏差应力、破坏比和初始切线模量；

3)基于不同Dr，以不同围压σ3下对应的粗颗粒土峰值应力(σ1-σ3)f为条件，作出lg[(σ1-σ3)f/pa]—lg(σ3/pa)关系曲线，根据该关系曲线形状，确定出适合粗颗粒土的Dr与峰值应力(σ1-σ3)f关系曲线；

4)基于不同Dr，以不同围压σ3下对应的粗颗粒土初始切线模Ei为条件，作出lg(Ei/pa)—lg(σ3/pa)关系曲线，并以该曲线确定适合粗颗粒土的Dr—K关系曲线;

5)结合统一扰动度函数DD，Dr-Ei曲线和Dr—峰值应力(σ1-σ3)f曲线，推导出仅含有相对密实度Dr,破坏比Rf的双曲线型粗颗粒土应力—应变关系；并基于Dr—K曲线和Dr—峰值应力(σ1-σ3)f曲线，确定出本构模型中无量纲参数的取值，得到考虑扰动影响的粗颗粒土非线性弹性本构模型。

利用上述步骤得到的考虑扰动影响的修正D-C模型形式如下：

(2)

其中，n为lg(σ3/pa)与lg(Ei/pa)的关系曲线斜率；l为试验常数，对于同一土体，l的值相对稳定，趋近于定值[5]；pa为标准大气压力。

3 结果对比分析

3.1 修正D-C模型结果汇总

本文以三种常见粗粒土，进行多围压条件下的CD试验，通过修正,得到全新的扰动D-C模型，结果如表2，表3所示。

表2 不同种类粗颗粒土拟合形式选取汇总表

表3 考虑扰动的粗颗粒土修正D-C模型参数

3.2 结果对比分析

为验证本文提出的修正D-C模型在预测应力—应变关系时的合理性，以圆砾为例，针对不同Dr条件(围压200 kPa工况)，笔者应用本文提出的式(2)对扰动圆砾土体力学行为及特性进行预测，并对比CD试验数据及D-C双曲线。D-C模型相关参数列于表4；不同Dr条件对应的扰动度DD列于表5。

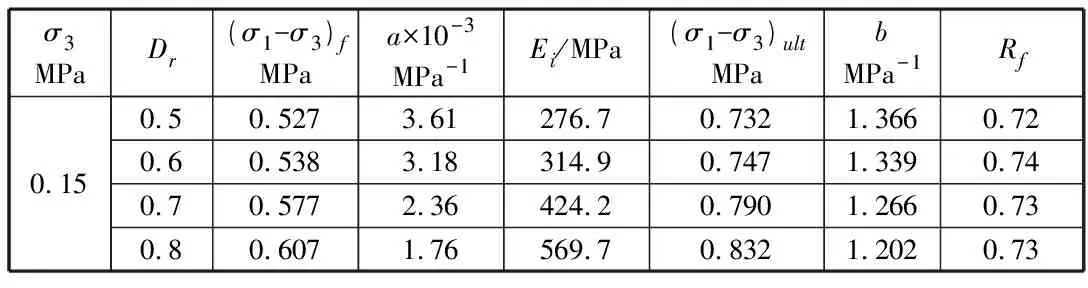
表4 圆砾土样D-C模型计算参数

表5 试验圆砾土扰动度DD

由于试验中圆砾试样颗粒排列紧密且级配良好，试验中圆砾试样呈剪胀趋势，可判别为应变软化土体，在大应变时，本文修正模型的预测结果与试验曲线有一定的偏差。但在实际工程中，绝大部分情况下粗颗粒土处于小应变状态(ε3∈[0.01%,0.3%]),基于此，本文后续仅对侧向应变在0%～3.0%范围内的预测结果与试验曲线进行对比分析，结果见图1。

由图1结果可知，对于扰动圆砾土体，在正(负)扰动状态,本文考虑扰动修正模型计算拟合曲线的拟合度更高；而D-C模型只在非扰动状态下与试验结果拟合良好。

4 模型应用

考虑扰动影响的修正D-C模型虽相应增加些许无量纲参数，但参数均较易通过三轴试验获得，便于应用在实际岩土工程问题的分析中，且较原始D-C模型，本文修正模型得到应力应变关系中更接近于实际试验工况结果，模型精确性更高。

对于该修正D-C模型及修正方法的后续发展及推广应用，可侧重于如下几点：

1)反映土体扰动的物理参数众多，因此，有必要开展围绕密度、含水量等参数变化对粗颗粒土体扰动的试验研究，提出相应的新型本构模型，后续还宜将相关参数引入至扰动状态函数，提出更多、更新的多维度扰动函数，丰富及拓展扰动本构模型。

2)粗颗粒土材料在我国分布范围较广，但地区性差异较大，因此采用此法获得的扰动本构模型存在一定差异性；前期应针对不同地域进行相关基础试验，积累经验，并适时提出通用性较强的修正本构模型。

3)应及时将自定义的扰动修正D-C模型的子程序植入现有商用有限元软件，方便实际工程应用，优化程序，提高效率；后续亦可考虑实际土体的孔隙比分布，研究同一工程中不同区域的相对密实度分区计算，使该子程序对粗颗粒土的描述更接近于真实情况。

5 结语

1)以相对密实度为载体进行考虑扰动影响的D-C模型修正过程中，相对密实度的变化会对原始模型中的参数K及峰值强度产生巨大影响，而对于模型中的其他试验参数影响微小，因此，本文扰动本构模型修正方法在实际工程问题应用中，可仅对此二参数进行修正。

2)通过试验结果分析，本文提出的粗颗粒土修正D-C模型，在考虑土体扰动的施工过程中，相比于传统邓肯—张模型，拟合曲线更接近于真实试验曲线，因此，采用该扰动修正D-C模型可更好的模拟实际工程中的扰动问题。

3)后续研究应采用此修正方法将扰动度植入现有不同地域及采用弹塑性力学理论的本构模型，并及时实现程序化，方便实际应用。