扰动累积下基于机器学习的重调度方式选择

2019-03-06 03:25:58唐秋华成丽新张利平

中国机械工程 2019年4期

唐秋华成丽新张利平

1．武汉科技大学生产系统工程研究所，武汉，430081 2．武汉科技大学冶金装备及其控制教育部重点实验室，武汉，430081 3．武汉科技大学机械传动与制造工程湖北省重点实验室，武汉，430081

0 引言

制造系统中，存在到达时间不准及操作时间波动等不可避免的隐性扰动。短时间的隐性扰动对生产调度没有显著影响，但隐性扰动的持续性累积很可能会干扰生产运行，迫使生产过程无法按照原定计划执行，而需进行重调度。目前面向隐性扰动的重调度研究较少[1]，主要原因是隐性扰动以累积的形式对生产过程进行干扰：当累积效应在可控范围内时，无需启用重调度；当超出受控范围时需启动重调度。这导致是否启动重调度的决策成为隐性扰动区别于显性扰动的关键。另外，对于选择何种类型的重调度方式，如完全重调度(TR)、右移重调度(RSR)还是局部重调度，也需深入研究[2]。由于面向隐性扰动的重调度与具体生产情形有关，具有多变性和复杂性，故现场管理时主要采用人工调度。然而，由于生产产品类型增多、调度所需信息指数增长、调度员知识结构和经验水平有限等，人工调度决策的稳定性、较优性很难保证，在某些情形下甚至无法保证可行性。故而，亟需研究扰动累积下基于学习的重调度方式选择框架，以便调度员快速、准确、智能地响应生产状况。

在不同生产情形下同时完成重调度方式智能选择及重调度时刻点决策的研究相对较少。PETROVIC等[3]以生产持续时间和原材料缺货量为参数描述生产过程的不确定性,建立了基于模糊推理的重调度决策系统。乔非等[4]引入最小重调度时间间隔约束，避免混合驱动策略中出现重调度触发点间隔过小或过大的现象，保证系统实时性和稳定性。单晖[5]、陈静云[6]、JIANG等[7]研究了基于实时工况的动态自适应重调度决策机制。刘明周等[8]提出基于损益云模型的重调度决策方法，实现重调度触发判定及调度方案的选取。刘壮等[9]、AKKAN[10]采用被动触发式重调度驱动规则对隐性扰动的重调度决策进行研究，提出基于改进TOPSIS的重调度决策方法。然而，现有重调度研究集中于给定扰动情形下的重调度方法和重调度策略优化，缺少具有普适性的重调度决策框架；此外，基于实际生产情形的数据获取代价较大，而且实际上也不可能获得完备数据集、不可能让采集样本覆盖全部生产情形。

为此，本文提出了一种隐性扰动累积下基于学习的重调度决策机制。

1 问题描述

隐性扰动问题复杂多变，基于学习的扰动累积下重调度方式选择问题需将隐性扰动量化，用数据表征生产状况。此外，由于隐性扰动的累积效应，需决策何时启动重调度，进一步需确定启用何种重调度。

1.1 基于累积误差时间的隐性扰动量化

在实际生产中，加工时长变动、生产物流衔接等，都会导致工序开始加工时刻的变化。

累积误差时间即实时累积延迟，针对工件而言，是其工序实际/计划开始时刻的差值。若某工件的每道工序按计划开始，则其累积误差为0；若提前开始，则累积误差为负；若滞后开始，则累积误差为正。累积误差反映了前面各道工序执行状况对本道工序开始时间的显著影响，故可用累积误差时间来量化隐性扰动的影响程度。

1.2 重调度时刻点确定

对于隐性扰动问题，判定重调度启动与否的具体时刻点对重调度的使用频次、车间稳定性和生产连续性具有较大的影响。当累积误差为正时，实际调度已经显著偏离计划，有可能出现交货期延迟等问题。由于鲁棒优化下的原计划调度具有一定程度的抗干扰能力，可削弱隐性扰动的影响，故将实际生产中累积误差为正的任务开始时刻选为重调度时刻点，在一定程度保持系统稳定性并对生产状况进行响应。

1.3 重调度方式及其优化决策

常见的重调度方式有多种，如右移重调度、完全重调度。右移重调度不改变后续工序的操作顺序，但调整其开始时间；完全重调度需对操作顺序和开始时间均作调整。不同的重调度方式会导致不同的制造周期和调整成本，故在不同的扰动累积情形下，要决策其最优重调度方式。

基于学习的重调度方式选择，是在海量带标签样本的基础上，通过采用机器学习等方法，决策不同扰动累积情形下的最优重调度方式。其中，每个数据样本均以最优重调度决策方式作为标签。

1.4 扰动累积下重调度方式优化决策模型

(1)

(2)

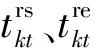
重调度数学模型约束条件可表示为

(3)

∀k,t=T

(4)

(5)

(6)

(7)

(8)

(9)

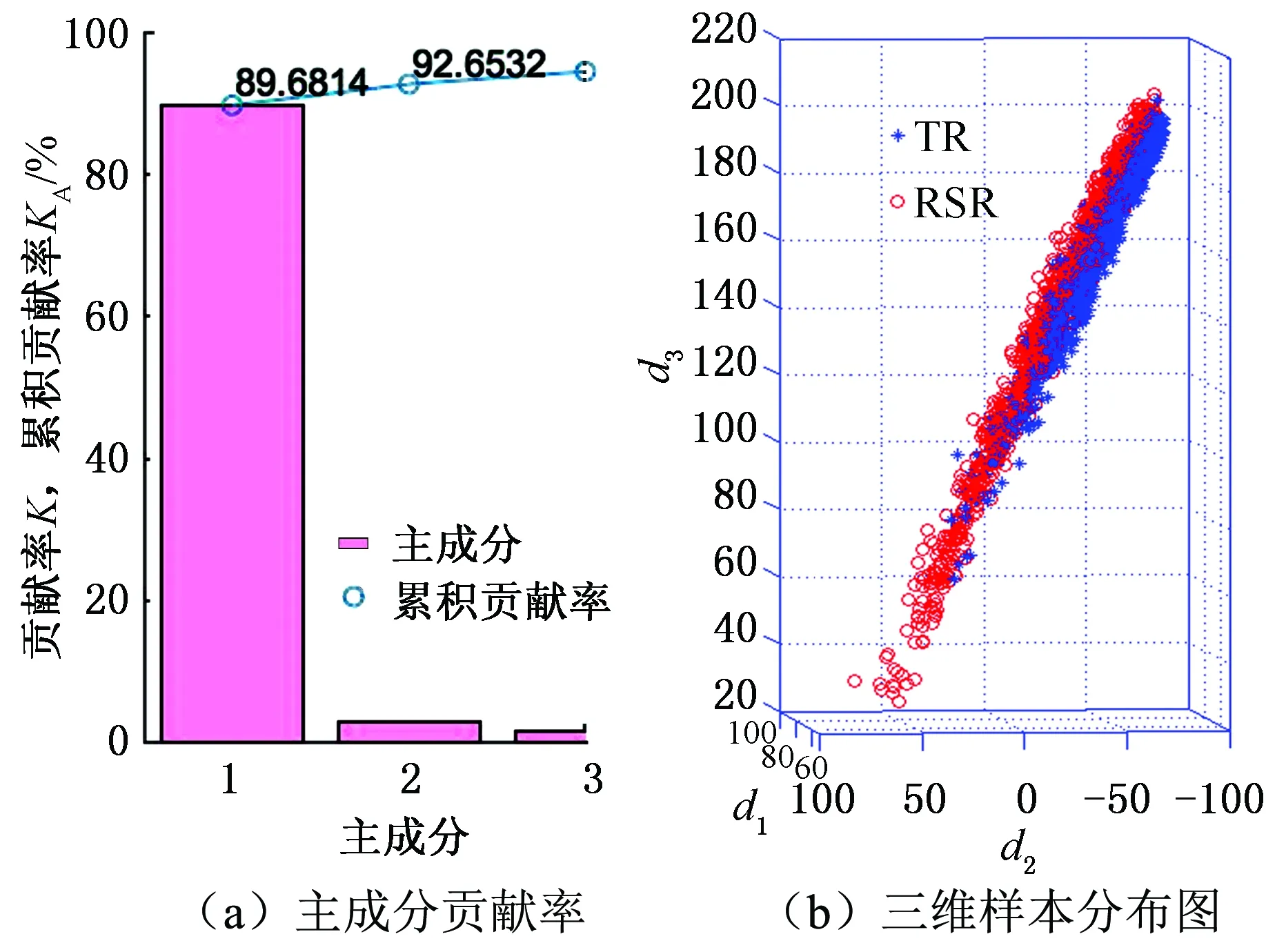
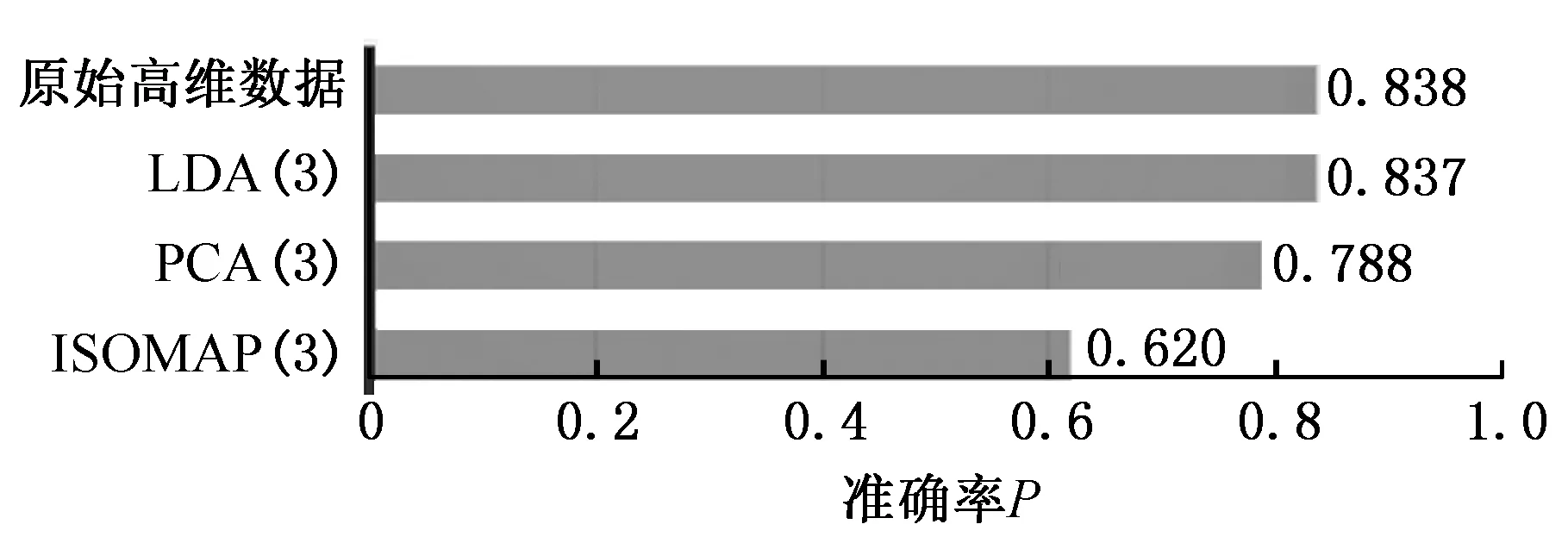
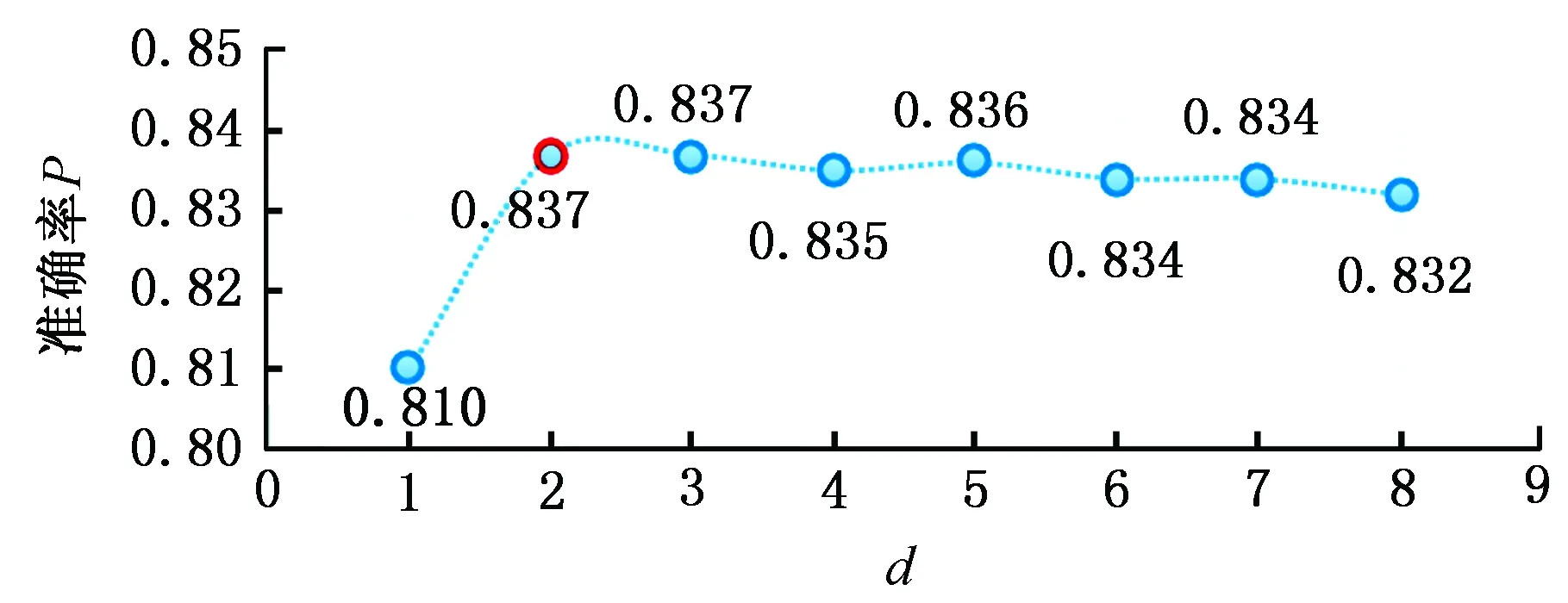
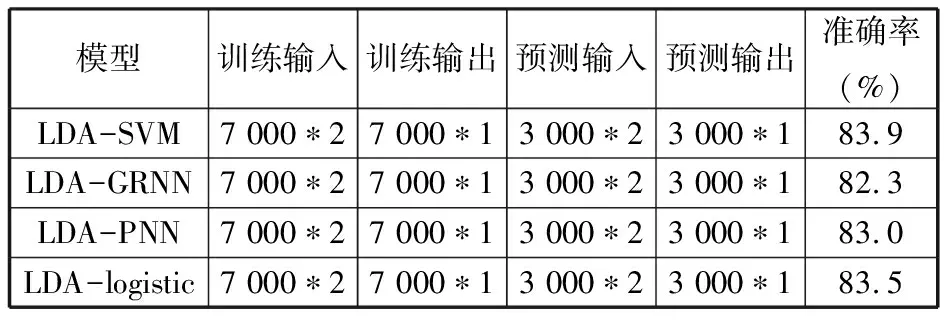
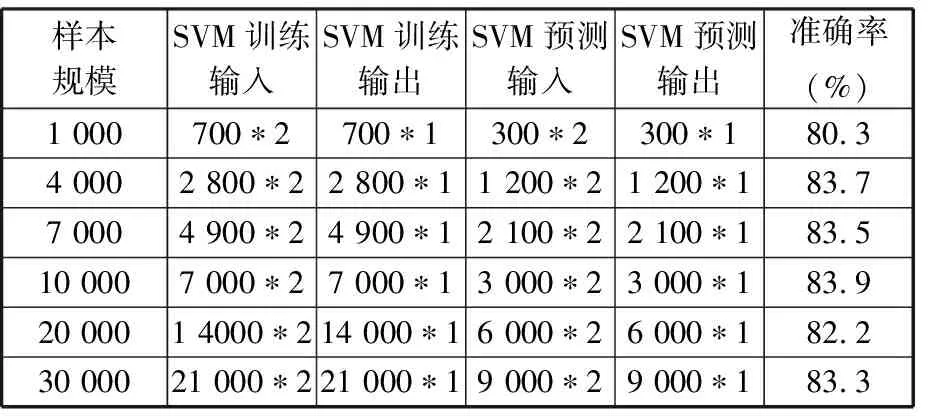
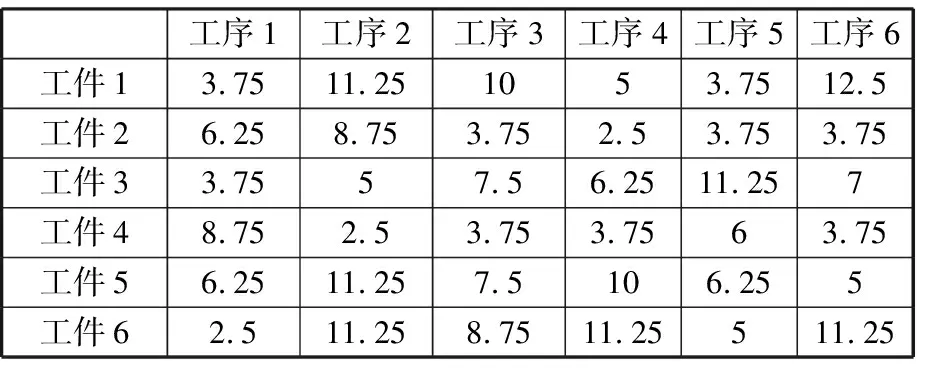
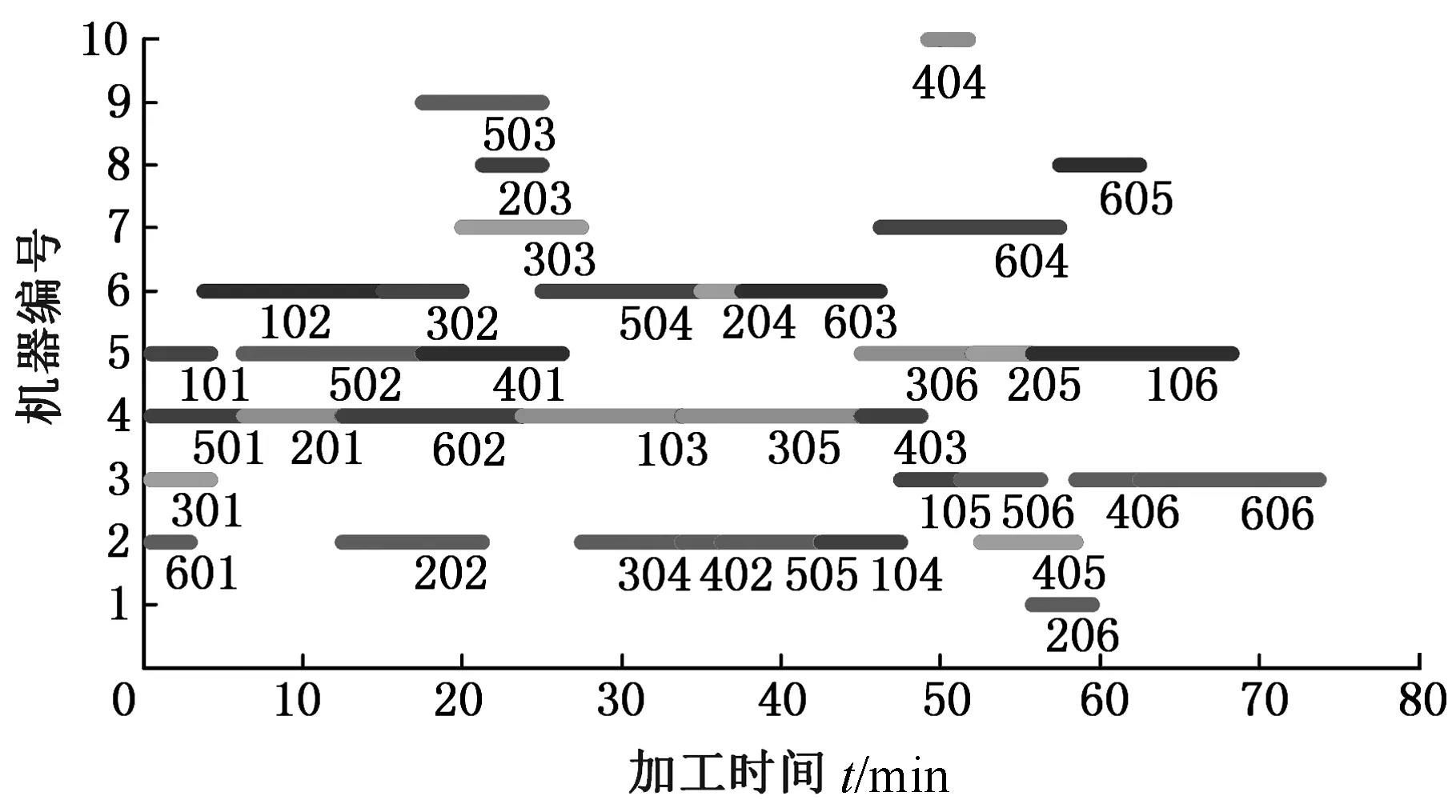
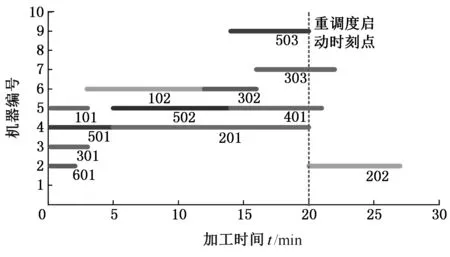
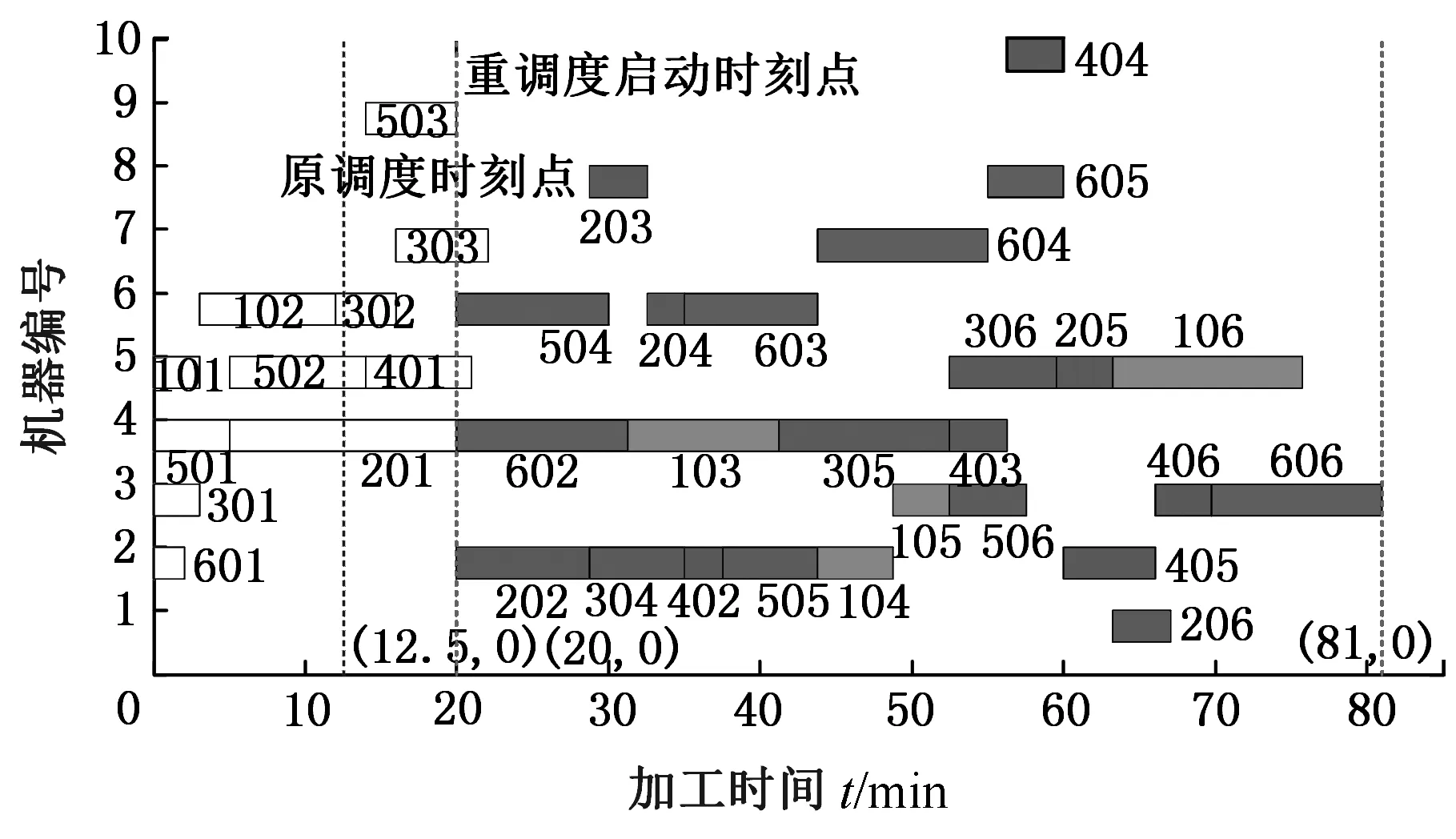
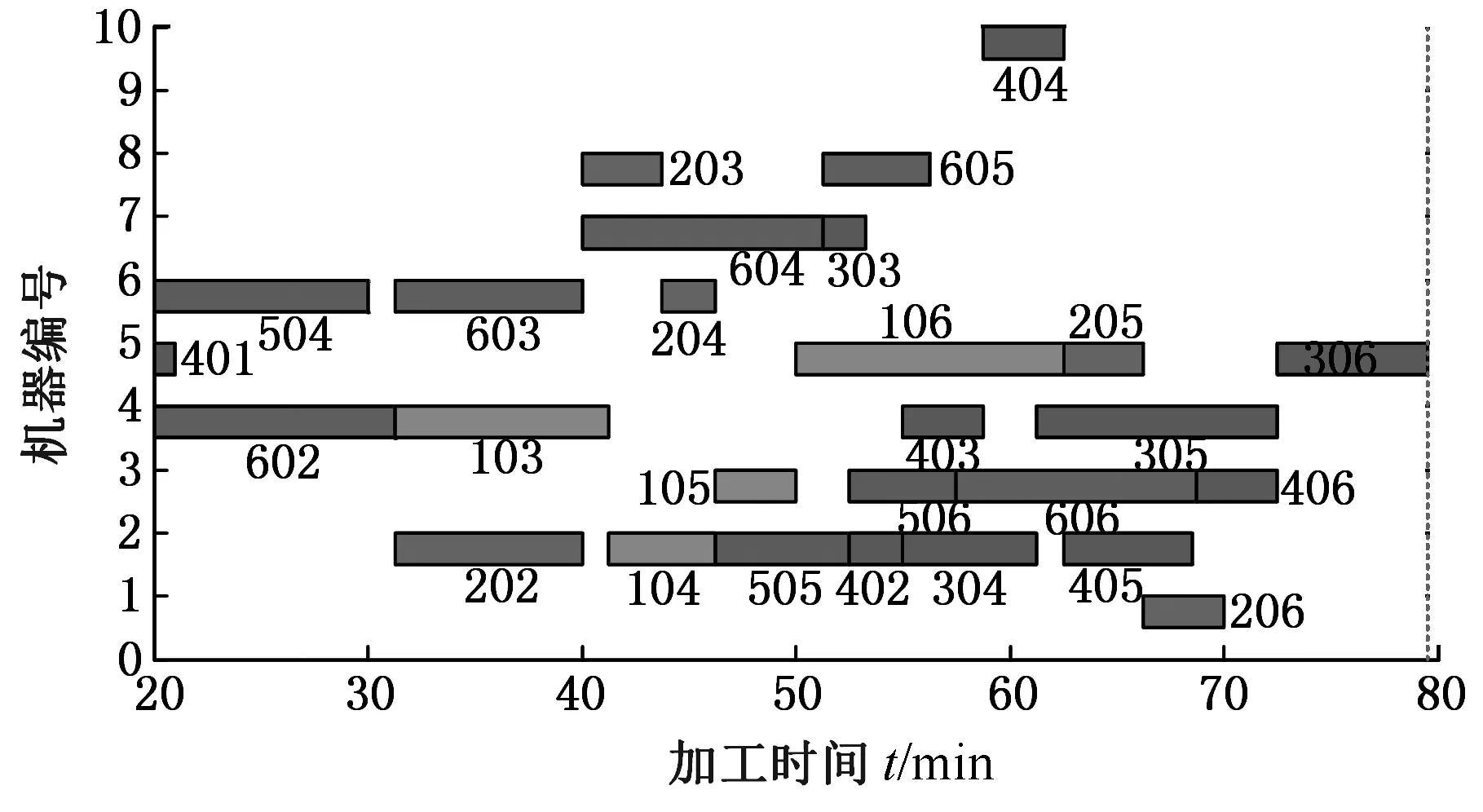
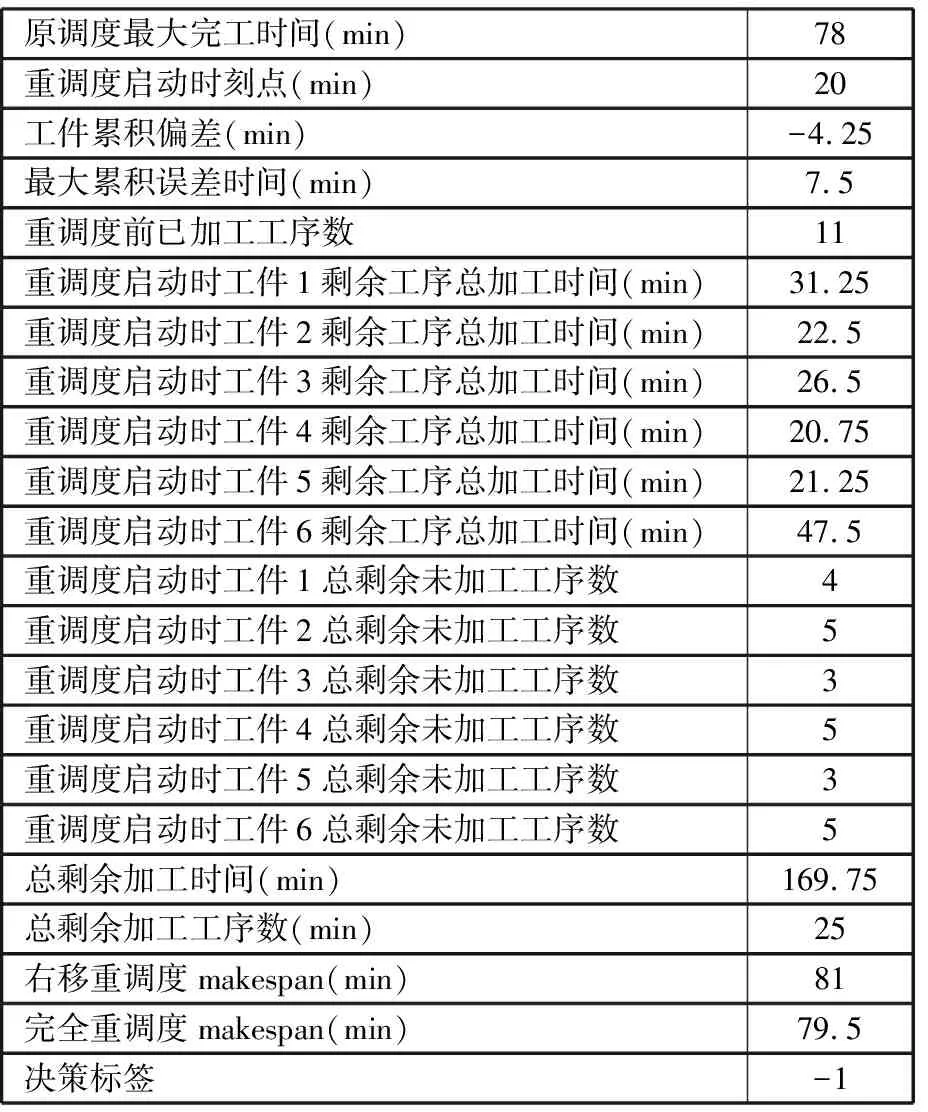
∀i,j

其中，式(3)表示不同重调度方式下的制造周期；式(4)表示在任一机器上的加工次序t，最多可执行一道工序；式(5)表示尚需加工的任一工序oij，只能在某一机器的某一加工次序上完成；式(6)表示在任一台机器上，只有在前一个加工次序已被分配任务的前提下，才可分配任务给随后的加工次序；式(7)表示在任一台机器上，前一个加工次序t的任务完成后，下一加工次序t+1任务才能开始；式(8)表示启动重调度后，所有剩余工序的开始加工时间大于或等于t0；式(9)表示对加工同一个工件先后两个工序的两台机器而言，需要排在前面的机器k的加工次序t完成后，才能开始机器k′的加工次序t′。

重调度方式选择的目标函数可表示为

(10)

由于右移重调度只调整了工序的开始结束时间，并未调整工序顺序，其模型可用式(3)、式(7)～式(10)描述；当采用完全重调度时，工序顺序和加工时间都有变化，故需用式(3)～式(10)描述。

1.5 基于学习的重调度方式选择框架

为实现快速、智能、实时决策，本文构建了图1所示的基于数据学习的重调度方式选择框架。具体包括重调度大样本生成、重调度选择模型构建以及实际生产中重调度方式选择模型应用。

图1 重调度方式选择框架Fig.1 Framework of rescheduling mode selection

2 融合鲁棒计划和扰动累积的重调度样本生成

由于设备、技术等原因，直接从实际生产中获得所需的研究数据代价极大。本文通过模拟仿真产生实验研究数据，将隐性扰动问题量化，用数据反映现实加工状况。如图2所示，所采集数据包括重调度前、重调度启动后表征生产状况的数据，以及重调度方式选择标签数据。

图2 数据采集框架Fig.2 Framework of data acquisition

(1)加工数据生成。隐性扰动造成工序加工时长变化，从而改变原调度计划，故可利用3种随机数改变加工时长来生成大量加工数据以模拟实际扰动：第一种随机数是产生扰动的工序总道数；第二种是某个工件的某道工序产生的扰动；第三种是扰动量大小。各工序鲁棒阈的设定是将归一化的原加工时长作为权重乘以(0,1)之间的随机数。

(2)重调度前评价因素。基于遗传算法生成鲁棒优化最优调度方案，并与实际生产调度中各工序开始加工时刻对比，获得累积误差时间进而确定重调度时刻点。此过程中考虑从加工周期(makespan)、累积误差时间、重调度前工序加工状况几个方面评估生产状况。

(3)重调度后评价因素。分析和处理需要进入重调度的工序。此过程可用进入重调度的工序加工情况评估生产状况。鉴于前期文献缺乏此方面的研究，故考虑因子时应尽可能多地收集与生产状况有关的数据。此外，限于篇幅，将在后续单样本实例中具体展示所需因子数据。

(4)决策标签。利用重调度模型得到右移和完全重调度的最大完工时间，若两者差值为负，则选右移重调度并标记为1，否则为-1。

(5)获取大样本数据。重复以上步骤，可获得多维样本数据(最后一维是决策标签)。

3 数据处理与选择模型构建

3.1 样本数据清洗

数据样本的质量对数据分析以及模型建立有直接影响。以下是针对所采集数据的初步处理。

(1)缺失值。采用平均值填充方式对数据进行处理。

(2)异常值。不同于以往定义，考虑将累积误差时间都小于0(未启动重调度)的数据作为异常数据，此类数据生成无效，直接丢失。

(3)平衡两类样本。通过使用重复、自举或合成少数类过采样(SMOTE)等方法来生成新的稀有样本。

3.2 样本数据分析

不同特征数据的处理方式不一样，故在运用数据建模之前，有必要对数据特征进行简单分析，了解数据形态。

图3统计了36个工序、4 000个样本获得各自在不同重调度时刻点的生产情形。它表明生成的样本中，除已加工工序数{1,2,35}没有对应样本外，其他重调度情况都有对应样本。此结果表明，除极端情况外，生成的样本能有效覆盖实际生成状况。

图3 样本整体概括Fig.3 Sample generalization

此外，为检验数据的相关性，对数据进行了皮尔逊相关性分析，结果见表1。标注*号的数据表示相关性显著，从相关性系数可看出很多数据间呈强相关关系。

3.3 基于线性降维方法的数据降维

数据降维一方面可降低计算代价、实现可视化、便于理解，另一方面有利于有效信息的提取综合、无用信息的摈弃[11]。通过数据分析结果可知，样本因子数据间相关性强、带标签，故考虑采用有监督的线性降维方法(linear discriminant analysis，LDA)进行数据降维。

表1 皮尔逊相关性

设重调度样本D={(x1,y1),(x2,y2),…,(xm,ym)}，y为重调度决策标签，yi∈{-1,1}，Nj为第j类样本的个数，Xj为第j类样本的集合，μj为第j类样本的均值向量，Σj为第j类样本的协方差矩阵,则有

(11)

(12)

j=-1,1

为保证同一重调度方式样本的投影点尽可能接近，而不同重调度方式样本中心之间的距离尽可能大，将LDA模型简化为

(13)

3.4 SVM分类决策模型

分类预测方法众多，如决策树、贝叶斯分类器等，但不同分类器对数据特征的要求不同，如贝叶斯分类器、决策树等不易于对样本属性值连续的数据进行分类预测；而神经网络训练分类器时，其训练过程是使网络全局误差趋于极小值，易出现过拟合状况从而使预测准确率降低；支持向量机(support vector machine, SVM)训练的分类器在解决连续属性分类问题上有一定成效，能在分类准确的基础上，最大化容忍犯错，有效避免过拟合，较好地对二类问题进行分类预测[12]。由于重调度方式选择的样本数据属性连续,故考虑用SVM进行分类预测。

在SVM中，支持向量表示在线性可分的情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例。定义y为重调度决策标签,y∈{-1,1}，ω为法向量，b为偏置，n为重调度样本总数，xi表示第i个样本,则有

(14)

(15)

式(14)为一般计算点到直线的距离d的公式。在SVM中，式(15)描述函数能够正确划分点到超平面(能将两类重调度方式样本分隔的面)的距离dd。若定义支持向量到超平面的距离为1，即y(ωTx+b)=1,为保证模型准确，其他样本需满足y(ωTx+b)>1,此时SVM模型求解过程变为

(16)

4 实验

4.1 不同降维方式对比实验

为证实所选降维方法LDA的有效性，以非线性降维ISOMAP和无监督线性降维主成分分析(principal component analysis, PCA)为代表，进行对比实验。

其中，ISOMAP是一种等距映射算法。利用ISOMAP降维时，从二维到三维残差方差下降最快，将数据降到三维时，两类数据样本分布见图4。

图4 ISOMAP降维Fig.4 Dimension reduction of ISOMAP

利用PCA对数据降维，前三个主成分贡献了92.65%的信息，将数据降到三维时，两类数据样本的分布图见图5。可看出其分类效果优于ISOMAP，说明采用PCA更有利于不同扰动累积情形下的重调度方式样本数据分类。

图5 PCA降维Fig.5 Dimension reduction of PCA

对比线性无监督降维PCA与线性有监督降维LDA可知， PCA方法不考虑数据标签，只选择样本点投影具有最大方差的方向，而LDA使得同类样例投影点尽可能接近、异类样例投影点尽可能远离，因此选用LDA对此类数据降维更有利于样本的分类。

图6是基于LDA将高维大样本数据降到一维时的两类样本分布图，由图可看出第二类样本的数值基本小于第一类样本，两类样本基本可区分；图7是采用LDA将数据降到二维时两类样本的分布图，由图可看出样本点间虽有融合，但大体可区分。由于将数据降到3维以上时出现复数，其降维效果将以分类准确率的形式量化。

图7 二维样本分布图Fig.7 2D sample distribution map

为精确比较降维效果好坏，基于4 000个样本，用不同降维方法处理的数据训练了三维输入下的SVM模型，并进行预测。其中，训练样本与测试样本比例为7∶3。从图8可看出，直接用原始高维数据建立SVM模型，模型准确率83.8%，但数据维度高，存储和计算代价高；基于PCA的SVM模型，准确率为0.788，数据储存等代价降低，但可能由于损失了数据精度，准确率下降；基于ISOMAP的SVM模型，准确率为0.62；而利用LDA方法对数据处理后，模型准确率为83.7%，既去除了高维数据中的冗余信息，降低了计算代价，又保证了数据精度。

图8 不同降维方法的准确率Fig.8 Accuracy of different dimension reduction methods

4.2 LDA-SVM实验

为测试LDA降维维度对LDA-SVM模型的影响，实验中，从4 000组训练样本中随机抽取2 800组训练模型。训练模型输入由LDA处理得到，测试输入由LDA降维时主特征值对应特征向量映射得到，模型输出为对应决策标签。由图9可看出，基于LDA降维数据的SVM模型分类准确率在80%以上。与一维特征量相比，二维特征量表达的信息更多，分类准确率提升0.027。但数据维度降到三维以上时，由于数据冗余等干扰，分类准确率略有下降。

图9 分类准确率对比Fig.9 Comparison of classification accuracy

确定降维方式及最佳降维维度后，为测试LDA-SVM组合模型的有效性，在样本规模为10 000的实验环境下进行了表2所示实验。其中，训练样本与测试样本比例为7∶3。实验结果显示，同一样本下LDA-SVM预测准确率最高。

为进一步测试LDA-SVM模型的稳定性，需要进行不同样本规模下的模型测试实验。表3中，所有实验的训练、测试样本比例为7∶3，数据维度为2。表3表明，随着样本规模的改变，模型准确率稍有变动，但总体准确率保持在83%。此外，样本规模为4 000时，模型已学习到数据基本特征，尽管样本规模进一步扩大，准确率却难有提升，模型基本稳定。