基于客流均衡分析的城际铁路列车运行图优化

周文梁，张先波，屈林影，李鹏



基于客流均衡分析的城际铁路列车运行图优化

周文梁，张先波，屈林影，李鹏

(中南大学 交通运输工程学院，湖南 长沙 410075)

将城际客流均衡分配与列车运行图优化相结合，构建城际列车运行图优化的双层规划模型，其中，上层模型以满足行车组织要求、运营时间等为约束，以降低旅客乘车时间、换乘等待时间以及提高始发、终到时间满意度为目标优化列车运行图；而下层模型为基于列车运行图的客流均衡分配模型。模型采用模拟退火算法与GP算法组合求解，在生成初始列车运行图的基础上不断通过均衡分配乘车客流、构造邻域解迭代优化。算例分析表明模型与算法具有较好的收敛性与有效性。

城际铁路；列车运行图；客流均衡分配；模拟退火算法；GP算法

近年来城际铁路在我国多个城市群内得到了快速发展。作为旅客乘车选择依据的城际列车运行图，其编制质量决定了城际列车服务水平与运行效率，其优化对提高城际铁路在城市群区域客运市场竞争力具有重要意义。目前，较多研究基于列车运行组织与旅客乘车选择之间的主从博弈关系，借助于交通流理论均衡分配乘车客流，由此为依据优化组织列车运行。史峰等[1]将列车开行方案与旅客乘车选择结合起来，构建了旅客列车开行方案优化的双层规划模型与算法；彭其渊等[2]基于随机稳定性客流分配方法构建了旅客列车开行方案的多目标随机期望值规划方法；史峰等[3]结合弹性需求条件下的旅客乘车选择均衡分配，建立了基于弹性需求的旅客列车开行方案的双层规划方法。但以上研究仅是将乘车客流均衡分配结合到列车开行方案优化过程中，由于缺乏列车运行时刻信息，难以准确描述旅客乘车选择行为。列车运行图优化至今已取得了较多的研究成果。ZHOU等[4−5]以最小化列车旅行时间为优化目标，采用分枝定界法、定序优化方法等优化旅客列车运行图；Ghoseiri等[6]在最小化列车旅行时间外，还兼顾机车能源消耗、运行图均衡性等目标；汪波等[7−8]借助网络约束图及周期势差模型优化周期性列车运行图。黄鉴等[9]以时段需求为差别，提出基于分步循环的模拟退火算法实现运行图全局优化。但目前并没有考虑列车运行图编制与旅客乘车选择之间的相互影响，由于缺乏列车乘车客流与列车间换乘客流信息，优化过程中难以针对性地安排列车运行时刻。本文将城际列车运行图优化与旅客乘车选择结合起来，在列车运行图优化过程中通过均衡分配乘车客流而获得各列车乘车客流与换乘客流等信息，以此为依据对列车运行图进行迭代优化。

1 多目标双层规划模型

最小化列车旅行时间是列车运行图优化普遍采用的优化目标。然而，这仅能达到降低旅客乘车时间的目的。实际上，部分旅客出行还需花费一定的换乘时间，且随着旅客出行服务要求的提高，对始发、终到时间也有一定的要求。因此本文考虑以下优化目标。

1.1 压缩乘车时间

当时段OD对á,ñ旅客选择路径出行时，乘坐列车Î的上车站为、下车站为′，则其乘车时间为：

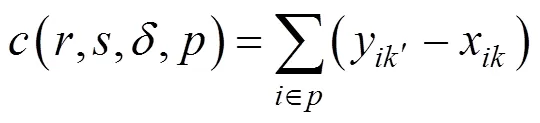
1.2 减少换乘等待时间

当时段OD对á,ñ旅客选择路径出行时，由列车换乘至列车所在的换乘站为，则其换乘等待时间为：

其中：h为旅客在换乘站换乘所需要的必备时间。

1.3 提高始发、终到时间满意度

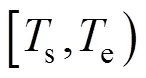
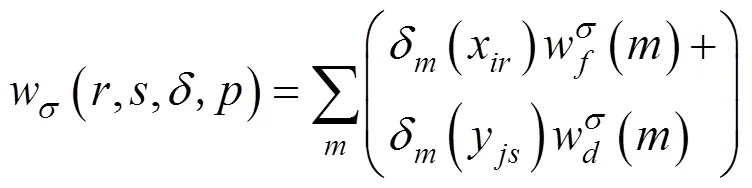
本文结合用户均衡分配模拟旅客基于给定列车运行图的乘车选择行为，构建以下列车运行图优化的双层规划模型。

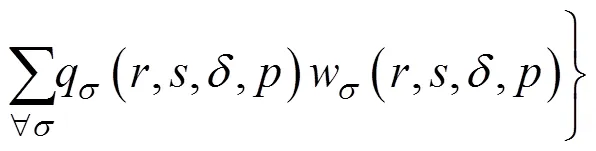
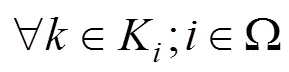
(9)

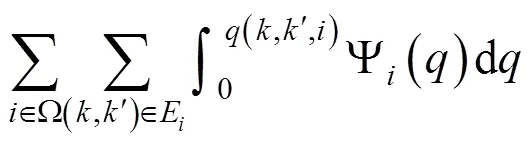
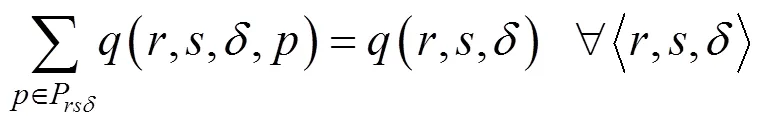
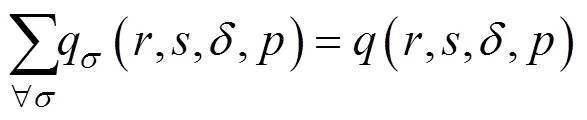
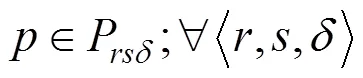
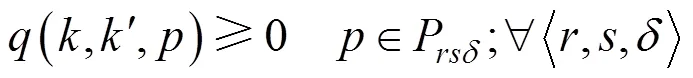
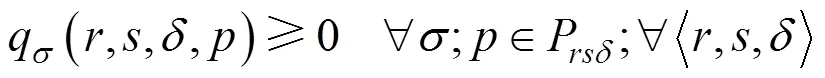
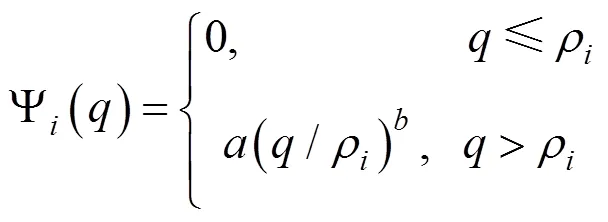
其中：和为拥挤费用参数。

以上双层规划模型中，式(5)表示列车区间运行时间约束；式(6)表示列车停站时间约束；式(7)与式(8)分别表示列车满足最小到、发达作业间隔要求；式(9)表示列车运行时刻满足城际铁路运营时间 约束。

2 给定乘车客流列车运行时刻计算方法

每列列车运行时刻的安排既要使得乘坐该列车旅客具有较高服务水平，同时又不影响已安排列车服务水平。对于列车，其乘车客流可分为以下 4类：

2.1 列车i为出行首列与末列列车

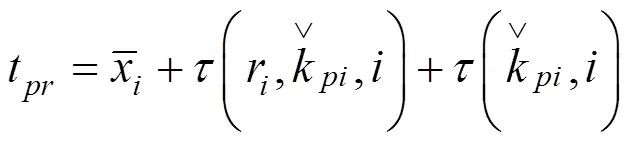
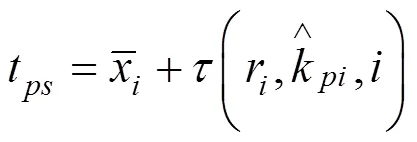
计算此类乘客的出行效益(即始发、终到时间满意度)如下：

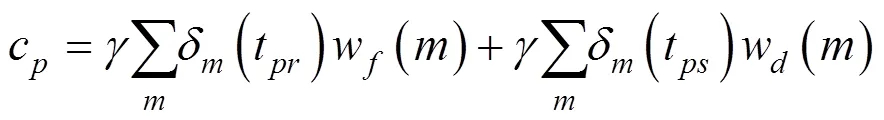
2.2 列车i为出行首列而非末列列车

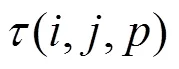
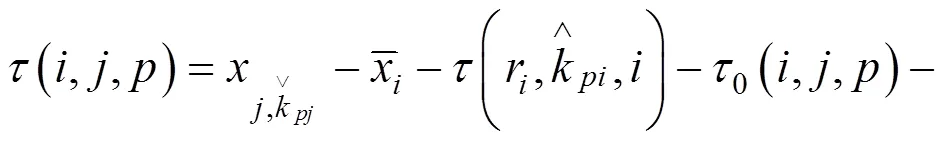
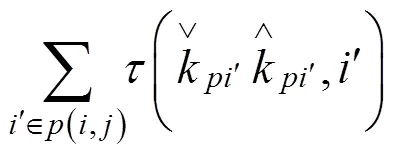
若该类乘客由列车换出后所乘坐的后续列车运行时刻均未计算，则假设乘客能够以零等待时间换乘至目的地，按式(16)计算始发时间，并按如下方法计算其终到时间：

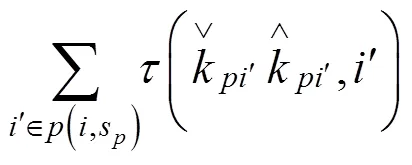
至此便可计算此类乘客的出行效益为：

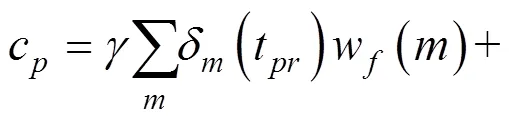
2.3 列车i为出行末列而非首列列车

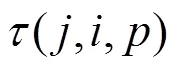
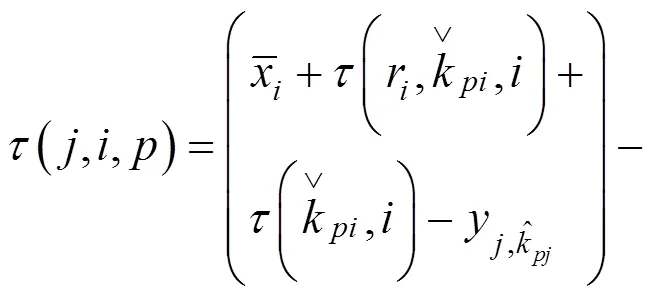
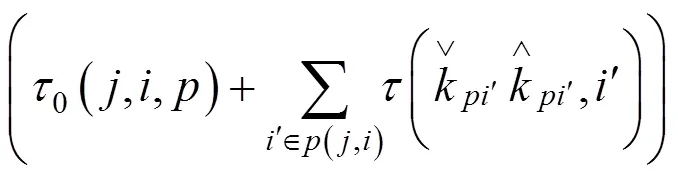
若此类乘车客流换入列车前所乘坐列车的运行时刻均未计算，则同样假设乘客能够以零等待时间从始发站换乘至列车，按式(17)计算其终到时间，并按如下方法计算其始发时间：

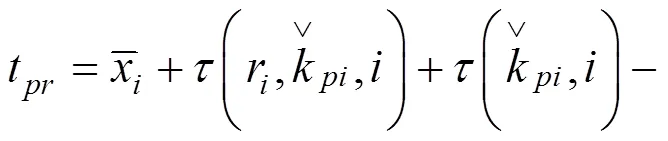
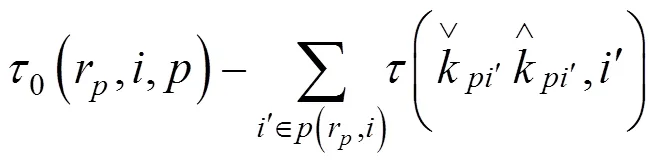
至此便可计算此类乘车客流出行效益为：

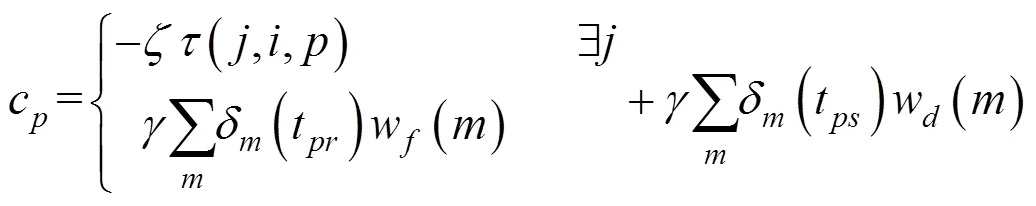
2.4 列车i既非出行首列也非末列列车

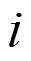
列车备选始发时段集的计算方法如下所示：

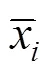
若路径乘客属于1和2类旅客，则

否则，

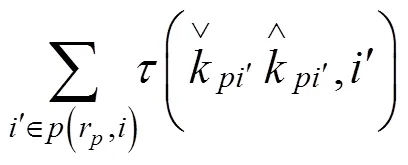
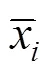
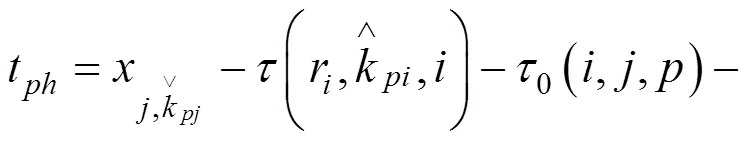
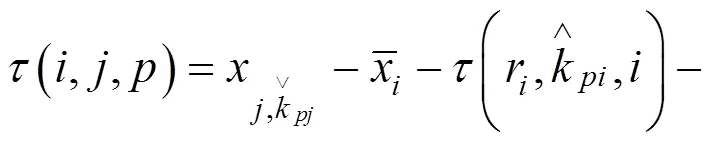
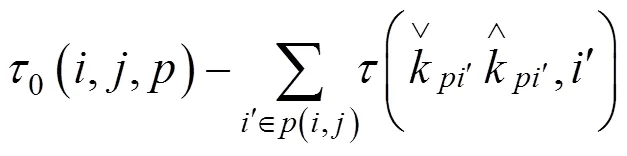
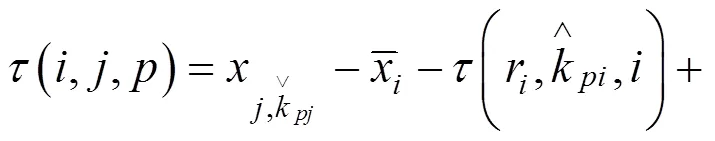
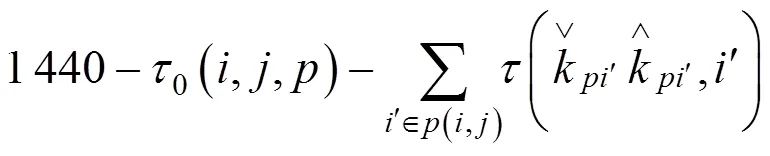
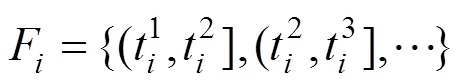
在按以上方法确定列车始发时段集F后，按旅客出行效益由大到小选择列车始发时段，若列车以当前选择时段的中间时刻发车可完成整列列车运行时刻推算，则输出该列车运行时刻；否则，继续选择下一个始发时段，重新计算列车运行时刻。

3 列车运行图优化算法

列车运行图优化属于NP-难问题。鉴于求解的复杂性，最优化算法难以在可接受时间范围内完成优化，为此本文设计模拟退火算法进行求解，同时将乘客客流均衡分配的GP算法嵌套其中。

3.1 初始列车运行图的生成

根据假定的理想出行条件的乘车客流均衡分配结果生成，具体如下：

1)旅客仅在给定的备选列车集中选择列车；

2) 旅客在任意换乘站以零等待时间完成换乘；

3)旅客乘坐任意列车均可获得最大的始发、终到时间满意度值；

4)任意列车在车站的停站时间均为所规定的最小值。

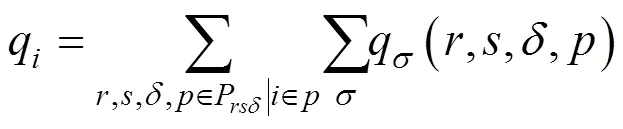
根据各列车载客量q由大到小顺序逐列计算列车运行时刻。

3.2 邻域结构设计

邻域结构决定了算法从当前列车运行图如何获得一个新的列车运行图，进而根据Metropolis准则判断新列车运行图是否被接受。具体按以下步骤产生新的邻域解。

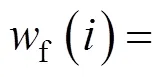
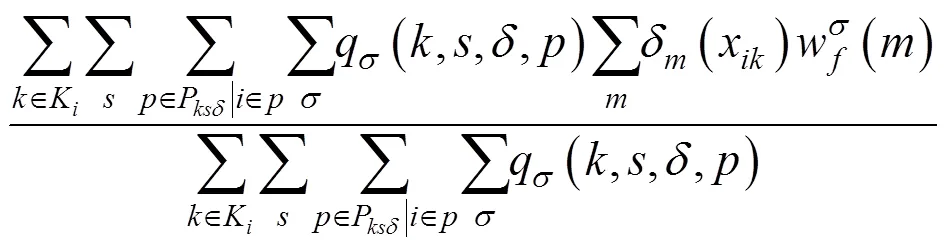
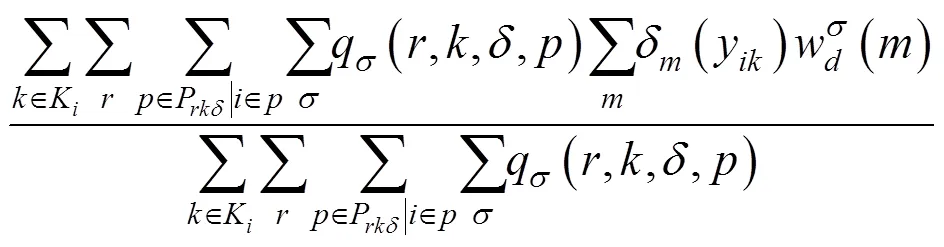
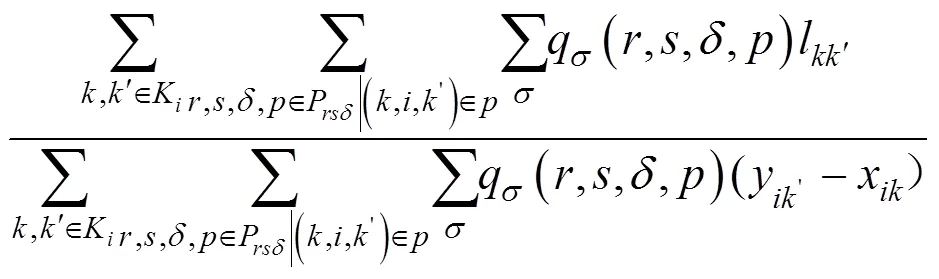
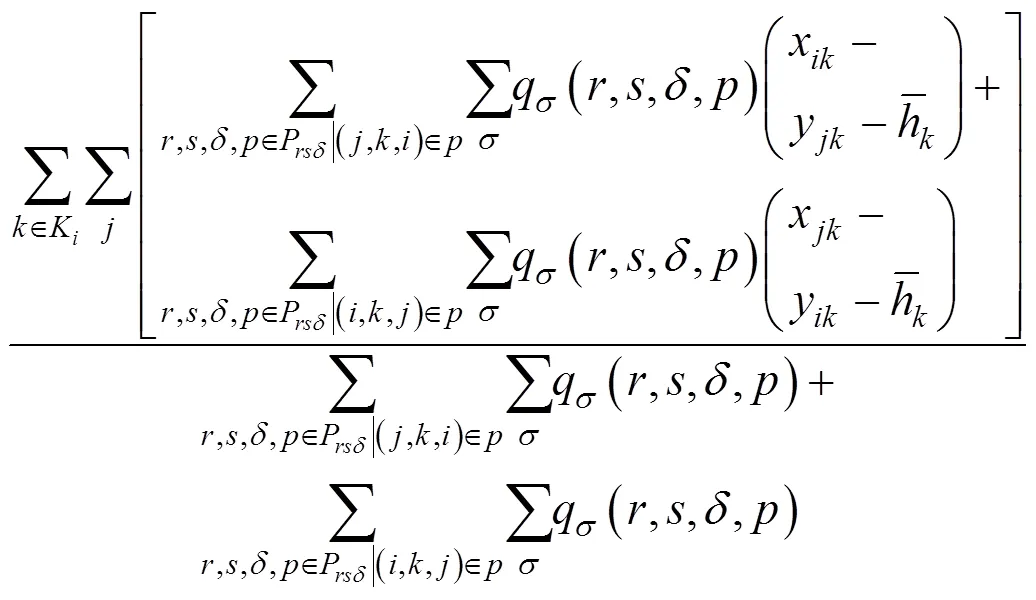
其次，分别以f(),d(),c()和h()为概率选择f，d，c和h列列车对其运行时刻进行重新计算，计算方法如下：

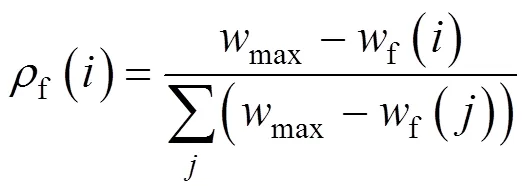
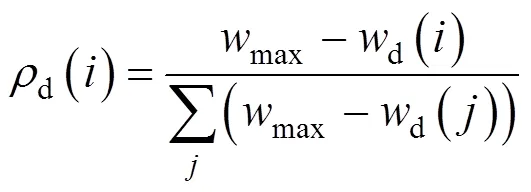
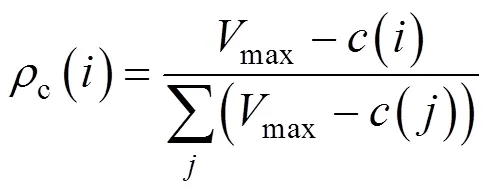
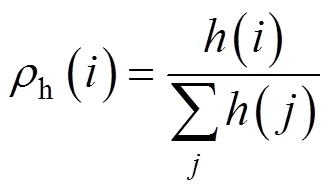
3.3 模拟退火计划表设计

模拟退火计划表控制了算法运行过程所需要的相关参数值，设计参数参考文献[3]。

至此，构建列车运行图优化算法如表1所示。

表1 城际网络列车运行图优化算法

4 算例分析

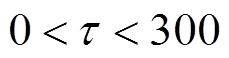
图1 算例城际网络

表2 列车运行径路

考虑路网上4个O-D对旅客出行，如表3所示。

表3 各OD对旅客出行需求量与出行路径

(a) α=0.80；β=1.20；(b) α=0.80；β=2.00；(c) α=1.20；β=1.20；(d) α=1.20；β=2.00

4.1 算法收敛性分析

为了分析算法的收敛效果与优化效率，取4组(,)值，如表4所示，其它参数取值保持不变，目标函数关于计算时间的变化如图2所示。由图2可知：随着算法不断迭代优化，所花费的计算时间不断增加，但同时目标函数值亦逐渐降低直至算法收敛。各情形下算法达到收敛时计算时间均大约为14 min，但实际上在运行10 min左右便已达到收敛解。由此表明该算法具有较好的收敛性，但相比而言，该算法收敛计算时间相对较长，其收敛速度有待改进，原因为乘车客流均衡分配消耗过多计算时间，尤其本算例将客流均衡分配算法收敛终止条件设置的较苛刻。

4.2 算法有效性分析

4组参数取值条件下旅客出行服务指标值如表4所示。旅客人均出行时间满意度均约为88，达到最大出行时间满意度的88%；人均乘车速度约为183 km/h，为列车最高运行速度200 km/h的91.50%；而人均单次换乘等待时间约为1.40 min。由此可见，由本文算法优化得到的列车运行图能够较好地满足旅客出行时间、乘车时间与换乘3方面的要求。

表4 4组参数取值条件下旅客出行服务指标值

各出行时间满意度值对应的旅客量占总客流量的百分比如图3(a)所示，各换乘等待时间值对应的旅客量占总换乘客流量的百分比如图3(b)所示。由图3可知，出行时间满意度为最高值100的旅客百分比达到60%以上，而以零等待时间换乘的旅客数量占换乘总人数的百分比达到65%左右，随着换乘等待时间的增加，相应的换乘旅客数量越小，旅客所花费的最大换乘等待时间为5 min。由此表明大部分旅客均能选择其最满意的出行时间出行，而且O-D 3换乘旅客所花费的换乘等待时间都较少。

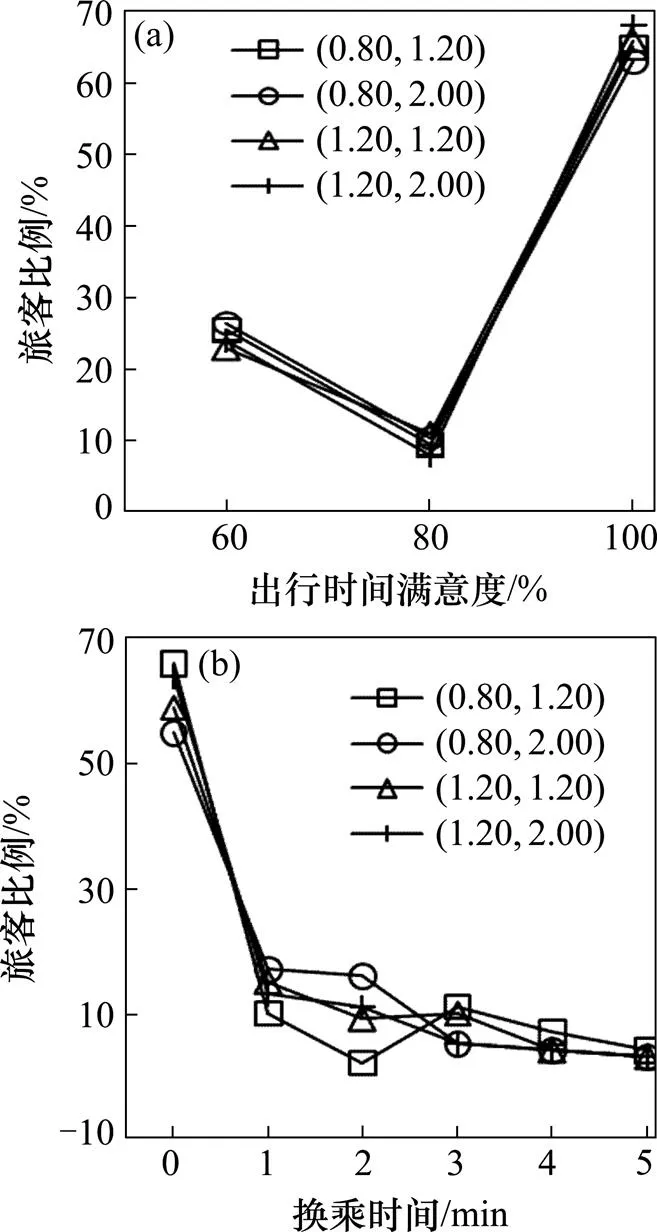
(a) 出行时间满意度；(b) 换乘时间

此外，由表4可知，和取值的变化对3组服务指标值并无较大影响；但由图2可知，不同和取值下目标函数的收敛值并不相同，随着和取值的增大，目标函数值收敛值也随之增加。经分析其主要原因为构成目标函数的3部分内容之间并不互相对立，其中任意一部分的改善，并不会制约另外两部分的改善，三者可以同时进行改善，但显然其权重值和增加将导致整个目标函数值增加。

5 结论

1) 结合不同出行目的城际客流乘车均衡分配，构建了城际列车运行图优化的双层规划模型，其优化目标由降低旅客乘车时间、换乘等待时间以及提高旅客始发、终到时间满意度3部分构成。

2) 设计模拟退火算法与GP算法来求解模型。

3) 通过算例分析表明本文该算法具有较好的收敛性与优化效果，但由于客流分配计算量较大导致算法收敛速度较低而有待改进。考虑城际铁路客流需求量与其列车服务水平的弹性变化关系来优化城际列车运行图将更符合实际。

[1] 史峰, 邓连波, 霍亮. 旅客列车开行方案的双层规划模型和算法[J]. 中国铁道科学, 2007, 28(3): 110−116. SHI Feng, DENG Lianbo, HUO Liang. Bi-level programming model and algorithm of passenger train operation plan[J]. China Railway Science, 2007, 28(3): 110−116.

[2] 彭其渊, 贾晓秋, 关晓宇. 随机稳定性配流规划的客运专线列车开行方案模型[J]. 西南交通大学学报, 2011, 46(1): 143−147. PENG Qiyuan, JIA Xiaoqiu, GUAN Xiaoyu. Train line planning model with stochastic stability in passenger flow assignment scheme for passenger-dedicated line[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 143−147.

[3] 史峰, 周文梁, 陈彦, 等. 基于弹性需求的旅客列车开行方案优化研究[J]. 铁道学报, 2008, 30(3): 1−6. SHI Feng, ZHOU Wenliang, CHEN Yan, et al. Optimization study on passenger train plans with elastic demands[J]. Journal of the China Railway Society, 2008, 30(3): 1−6.

[4] ZHOU Xuesong, ZHONG Ming. Single-track train timetabling with guaranteed optimality: Branch-and- bound algorithms with enhanced lower bounds[J]. Transportation Research Part B, 2007, 41(3): 320−341.

[5] LI Feng, GAO Ziyou, LI Keping, et al. Efficient scheduling of railway traffic based on global information of train[J]. Transportation Research Part B, 2008, 42(10): 1008−1030.

[6] Ghoseiri K, Szidarovszky F, Asgharpour M J. A multi-objective train scheduling model and solution[J]. Transportation Research Part B, 2004, 38(10): 927−952.

[7] 汪波, 韩宝明. 城市轨道交通网络周期运行图编制研究[J]. 铁道学报, 2013, 35(4): 9−15. WANG Bo, HAN Baoming. Study on formulation of periodic train diagram of urban rail transit network[J]. Journal of the China Railway Society, 2013, 35(4): 9−15.

[8] 谢美全, 聂磊. 周期性列车运行图编制模型研究[J]. 铁道学报, 2009, 31(4): 7−13．XIE Meiquan, NIE Lei. Model of cyclic train timetable[J]. Journal of the China Railway Society, 2009, 31(4): 7−13．

[9] 黄鉴, 彭其渊. 基于分时客运需求的客运专线列车运行图优化[J]. 铁道科学与工程学报, 2012, 9(6): 66−71. HUANG Jian, PENG Qiyuan. Train diagram optimization of passenger dedicated line based on passenger transport demand in different time[J]. Journal of Railway Science and Engineering, 2012, 9(6): 66−71.

[10] 周文梁, 史峰, 陈彦, 等. 客运专线网络列车开行方案与运行图综合优化方法[J]. 铁道学报, 2011, 3(2): 1−7. ZHOU Wenliang, SHI Feng, CHEN Yan, et al. Method of integrated optimization of train operation plan and diagram for network of dedicated passenger lines[J]. Journal of the China Railway Society, 2011, 3(2): 1−7.

Optimization of intercity railway train schedule based on passengers equilibrium analysis

ZHOU Wenliang, ZHANG Xianbo, QU Linying, LI Peng

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

This paper combined passengers’ equilibrium assignment to trains into intercity trains optimizing, and designed a bi-level programming model. The upper model was to optimize each train’s arrival and departure time at stations for reducing passenger in-train travel time and transfer time as well as improving their satisfaction to departure and arrival time under the requirements of trains departing interval time, minimum station dwell time, operating time, etc. And the lower model was the passenger equilibrium assignment model. This model was solved with the simulated annealing algorithm combined with GP algorithm, which continuously evaluates and adjusts the current train schedule for getting a better solution according to the result of passenger equilibrium assignment begin with an initial train schedule. Numerical example analysis shows that the proposed model and algorithm has good convergence and effectiveness.

intercity railway; train schedule; passengers equilibrium assignment; simulated anneal algorithm; GP algorithm

10.19713/j.cnki.43−1423/u.2019.01.031

U292.41

A

1672 − 7029(2019)01 − 0231 − 08

2018−01−12

国家自然科学基金资助项目(71401182, U1334207)

周文梁(1982−)，男，江西永新人，副教授，博士，从事轨道交通运营组织优化研究；E−mail：zwl_0631@csu.edu.cn

(编辑 蒋学东)