基于异类传感器观测信息融合的UKF算法*
杨菁华, 熊 智, 刘建业
(南京航空航天大学 自动化学院 导航研究中心,江苏 南京 211100)
0 引 言
在运动目标的探测与跟踪中,由于传感器探测原理的不同,往往需要多种不同的传感器配合使用才能获得对目标较完整的测量信息。异类传感器的搭配使用使得多传感器数据融合显得尤为重要,传统的方法是采用多只传感器的算数平均数,虽然有一定的抗干扰能力,但并不是最好的数据融合方法[1]。目前,多传感器信息融合算法主要有贝叶斯估计、加权平均法、极大似然估计、D-S证据理论、卡尔曼滤波等[2,3],由于人工智能理论的发展还出现了聚类分析、神经网络等现代融合算法[4]。但多数算法是针对同类多种传感器的数据融合,或在数据融合前对传感器进行处理,使传感器信息完成维数匹配[5],这类信息融合方法不能很好地适应无人机异类传感器配置时对目标的探测、跟踪。
针对异类传感器信息描述空间不同和信息维数不匹配的问题,本文以无人机目标定位跟踪为背景,提出一种基于异类传感器观测量扩维融合的无迹卡尔曼滤波(unscented Kalman filtering,UKF)跟踪滤波算法。经仿真验证,改进后的滤波算法能够显著提高目标定位精度。
1 总体方案设计
本文以高精度无人机目标定位为背景,以红外传感器和雷达的组合作为无人机探测手段,结合无人飞行器特点,本文建立以传感器直接量测量 (目标斜距、方位角和俯仰角)为量测变量的非线性量测方程,系统量测噪声方差阵直接从传感器获取,依次设计无迹卡尔曼滤波器,得到系统状态估计。总体方案设计如图1所示。

图1 总体方案设计
雷达、红外光电吊舱测量目标相对探测器的斜距、方位角和俯仰角,结合载机当前的位置和姿态信息,获得非线性量测方程并结合目标运动模型和UKF滤波器得到目标状态估计。
2 基于异类传感器观测量扩维融合的UKF算法
2.1 测量方程建模
采用文献[6]中基于齐次坐标转换的目标定位方法建立无人机的非线性测量方程,假设无人机机载传感器对目标的距离、方位角和俯仰角的测量值为(R,α,λ)T,目标在基座坐标系中的坐标为(xp,yp,zp)T,则传感器测量值和目标基座坐标系坐标值之间存在如下关系
(1)
根据文献[6]可以得到目标在大地直角坐标系中的坐标(xc,yc,zc)T与目标在基座坐标系中的坐标(xpypzp)T存在如下关系
(2)

式(1)和式(2)构成了无人机对高超声速目标的非线性量测方程,表示为
Z(k)=h(X(k),v(k))
(3)
2.2 异类传感器观测量扩维融合
假设传感器在无人机上为同步配置,且同步采样。目标的运动模型为
Xk+1=fk(Xk)+ΓkWk
(4)
式中Xk为系统的状态向量;fk为状态转移矩阵;Wk为系统状态噪声,且为零均值白噪声,其协方差为Q。
传感器的量测模型为
(5)
式中Zm为量测量,hm为非线性量测函数,Vm为量测噪声,且Vm为零均值白噪声,其协方差为R,m为第m只传感器,j为传感器种类。
当j=1时,传感器为三维雷达,则有
(6)
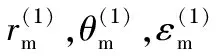
当j=2时,传感器为红外传感器,则有
(7)

将所有传感器测量信息进行扩维,则有
(8)
(9)
(10)
式中n为传感器数量。
扩维后的量测噪声方差为
R(k)=diag[R1(k),R2(k),…,Rn(k)]
(11)
扩维后的量测方程可以写成
Zk=hk(Xk)+Vk
(12)
2.3 基于异类传感器观测量扩维融合的UKF算法
UKF是以无迹变换(unscented transformation,UT)为基础,采用卡尔曼滤波框架,对于一步预测方程,使用UT来处理均值和协方差的非线性传递[7]。文献[8,9]指出,UKF的核心是利用不敏变换求取Sigma粒子,再把Sigma粒子通过非线性函数直接求取粒子的进化值,而避免了求取非线性函数的雅克比函数,且其精度可以达到二阶泰勒级数展开式。
对所有传感器观测量进行集中扩维处理可以得到一个由式(4)和式(12)组成的新系统。在该系统中,观测量为由所有传感器观测量扩展得到的向量。对新系统构建无迹卡尔曼滤波,其步骤如下:
1)初始化
2)计算采样点和权值
构造2n+1个采样点
(13)
式中λ=α2(n+k)-n,α决定采样点距离均值的远近程度,通常取值较小;k≥保证方差阵的半正定性。
计算权值为
(14)
式中β用于包含状态量分布的高阶成分信息,β≥0。
3)时间更新方程
(15)
(16)
样本点的测量预测为zi,k/k-1=h(χi,k/k-1)。
按照观测量扩展融合算法,采样点的测量预测增广得到采样点观测量扩展融合后的形式为
(17)
式中
(18)
(19)
系统的测量预测为所有采样点集中观测的加权平均值为
(20)
4)测量更新方程
系统测量预测协方差为
(21)
(22)
系统状态估计及其协方差矩阵分别为
(23)
(24)
3 仿真分析
本文采用MATLAB进行仿真实验,目标在初始位置(112.30°E,22.20°N,8 000 m),以200 m/s的速度,5 m/s2的加速度进行匀加速运动,载机初始位置为(112°E,22°N,5 000 m),设置载机配备有一只红外传感器和一个雷达,测量精度分别为:雷达测距为5 m,雷达方位角测量为0.03°,雷达俯仰角测量为0.03°,红外方位角测量为0.01°,红外俯仰角测量为0.01°。目标经度、纬度和高度方向的目标定位误差曲线如图2所示。

图2 误差曲线
由图2可以看出观测量扩维融合后的UKF滤波定位精度明显高于传统UKF算法,目标定位精度明显提高。
4 结 论
本文针对异类传感器由于信息描述空间不同,信息维数不匹配造成信息融合时需要处理使其完成维数匹配或无法对传感器观测信息进行融合的问题,提出传感器测量信息扩维融合的UKF算法,并运用在目标定位跟踪问题中,最后通过MATLAB仿真验证了改进后的UKF算法减小了目标定位误差,能够显著地提高目标定位精度,具有工程实用价值。

