基于改进量子遗传算法的油田井位及数量优化

,,

(1.长江大学 石油工程学院,武汉 430100；2.湖北工业大学 电气与电子工程学院，武汉 430068)

0 引言

为了提高油田开发效果以及采收率，许多技术，如注水驱油、二氧化碳驱油以及化学驱油等被陆续开发出来，这些技术都有利于于从油田储层中提取更多的石油，在开采技术的提高创新之外，适当的井位与合理的井数也是尽可能地提取石油并提高采收率的重要途径，因此，为了应对不断增长的世界能源需求，布井优化一直是行业内众多研究的焦点。

井位的优劣受油藏地质条件、流体特性以及开发时机等一系列复杂因素的影响，传统的井位选择方式是由人为制定若干并网方案，再采用数值模拟的方法选出一个较优的方案，该方案在理论上十分简便，但十分依赖方案制定者的经验，且从方案的制定到评价过程都十分耗时。布井的另一个问题是确定合理的井数，作为产油的直接渠道，油井的多少直接决定了油田的经济效益，油井太少，会使油田开发速度低下，无法满足生产任务；井数太多，油田的建设与维护成本也随之增加，且大密度的布井会造成油井间的相互干扰，降低油田经济效益。所以布井的优化问题往往是非线性且多模态的[1]。针对这种复杂的优化问题，建立合适的数学模型通过智能优化算法来进行求解是一种主流的处理方法。

目前，研究者们采用了许多各具特色的优化算法来解决布井优化问题。2010年，Bukhamsin[2]等，提出了一种多段井井位的优化方法，并采用了连续遗传算法(CGA)；2011年，Morales[3]等在利用遗传算法对井网优化的同时，引入了风险约束，使井位的分布更加合理；2013年，安瑶[6]等人运用了一种改进的粒子群算法对井位进行优化，并与遗传算法做了比较，证明了在速度方面PSO优于GA；同年，Lyons[4]等，将卡尔曼滤波与遗传算法相结合，在考虑了时间不确定性的情况下对井位进行了优化2015年，为了进一步提高优化效率，Sampaio[5]等提出一种混合算法，该算法将GA与共轭梯度算法(CC)相结合，算法参数设计合适的条件下，该算法具有良好的全局与局部最优的性能。从上述研究进程可以看出，在加速井位优化进程方面，结合多种机制的混合算法极具竞争力。

量子遗传算法(QGA)作为量子计算与进化算法结合的产物，量子理论中量子态相干、叠加与纠缠等特性大大 了传统算法中欠缺的并行计算能力，其计算速度与收敛效果均优于传统遗传算法，目前已逐步替代传统遗传算法应用于许多工程领域。因此本文在利用Matlab建立油藏数值模拟软件建立模型，将井数和井位作为变量，以油田净现值为目标函数结合QGA对井位进行优化研究。

1 模型建立

1.1 地质模型

为了精细描述油藏资源，本文利用Matlab软件在20×20网格上建立了一个非均质油藏模拟模型，该模型为一层，且厚度为50 m，X,Y方向上的网络步长为100 m。该油藏在开采时主要依靠其中所储存的油、水的弹性驱动，在没有外界能量供给的条件下将原油从地层驱至井底。本文在该模型的基础上以油田累计净现值最大化为目标，通过算法运算选取合适的布井位置及数量。油藏模拟模型如图1所示。

图1中油藏渗透率的变化范围为100～400 md，其分布场中各节点的渗透率值由Kriging(克里金)插值法生成。

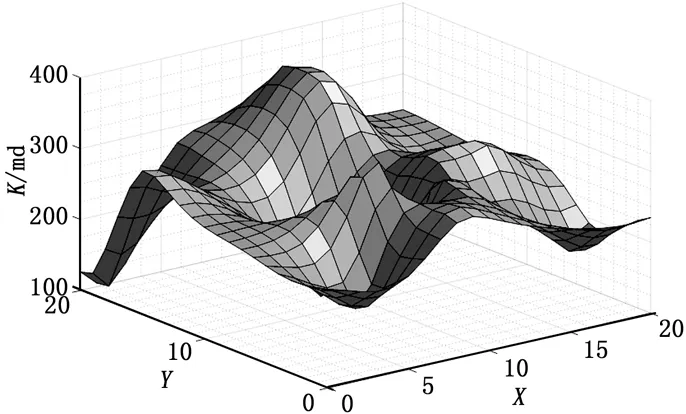
图1 油藏地址模型

1.2 数学模型

在地质模型的基础上，布井优化的数学模型将以井位及井数为变量并结合合理的目标函数共同构成。

本文的目标函数模型根据油田累计净现值建立。净现值(NPV)指在项目建设以及一定的生成年限内的现金流量根据折现率、通货膨胀率折算后得到的具体数值。本文中建立的NPV表达式为：

(1)

式(1)中，T为生产年限；δ为通货膨胀率；η为基准折现率；Cin(t)、Cout(t)为第t年的总收入及支出(元)，二者相减则为油田在第t年的净现金流量。其中：

Cin=PoQ(φ,k,x,y,n)

(2)

式(2)中，Po为原油价格；Q原油产量，根据油田实际开发过程中的影响因素，原油产量的决策变量主要由孔隙度φ、渗透率k、井位坐标x,y以及井数n构成。

Cout=nPm(Pinit,Pop,Pre)

(3)

式(3)中，Pm为总成本，其中包括建设成本Pinit、操作成本Pop以及维护成本Pre，为简化问题的数学描述，本文以单个井为单位计算各类成本。

通过上述分析，本文设立的目标函数最终形式为：

(4)

同时为了提高油田的安全性，消除油田生产工作时井间的相互影响，在布井时应当保持一定的安全距离。故本文将井距限制作为井位优化的约束条件，以井泄油半径作为井距限制，则有:

(5)

其中:dij为任意两井i、j之间的距离，Rj、Ri分别为井i、j的泄油半径。

2 改进的量子遗传算法

2.1 量子遗传算法简介

QGA作为量子计算与遗传算法相融合的产物，是一种结合了量子进化算法的多样性和遗传算法的全局寻优能力的混合启发式算法。

在QGA中，染色体不再由传统的二进制数或浮点数来表示，而是采用了量子比特的方式来表示，其特点在于该方法能同时表达任意叠加态，即单个量子位并不表示一个确定的数值，而是可以同时表示0和1以及他们之间任意的叠加状态。量子比特的染色体结构可以表示为：

(6)

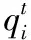
量子旋转门作为QGA中的个体进化策略，可根据具体问题进行选择，目前学者们针对不同的问题设计了许多量子选择门，其基本工作原理如下：

(7)

式中,αi和βi表示第t代染色体上第i量子比特通过旋转门更新前后的概率幅；θi为旋转角，其值根据算法策略事先设定，在算法进行时，将根据当前解与当前最优解之间相对应的部分基因的关系以查表的形式来选择合适的值替换。

与传统GA相比，量子比特的概率幅表示使得QGA更具并行性，在增加种群多样性的同时加快了算法的求解速度；量子门的种群更新方式也能在保持种群多样性的同时避免选择压力问题，提高了算法的搜索效率，使算法拥有更好的收敛特性。

2.2 改进的量子遗传算法

为了使量子遗传算法更好地解决所研究的问题，本文在标准量子遗传算法的基础上做出了改进。

量子遗传算法是进化算法与量子计算的结合，它对于初始数据的生成、数据的处理等方面偏向于进化算法的处理方式，而进化算法对于数据的处理方面具有一定的随机性，就本文数学模型的约束条件而言，对于随机生成的多个坐标，很难制定一条简便规则来保持它们两两之间的距离在一个定值之外。所以，为了简化算法，加快算法的计算速度，本文采取的改进方案受到蚁群算法的启发，将禁忌表策略与量子遗传算法相结合，使算法更好的处理井位的优化问题。

禁忌表是禁忌搜索的一个重要应用领域，其主要思想是在算法进程中，标记已搜索的局部里被约束条件所限制的对象，并在进一步的迭代搜索中避开这些对象。这种策略在本文中将嵌入到井位优化算法的初始种群生成以及种群进化的过程里，其方法如下步骤如下：

1)算法根据预设井数n，依次随机生成n个井位坐标。当第一个井位坐标生成时，将位于该坐标井距限制内的其余坐标全部纳入禁忌表Tabu；

2)当生成下一个井位坐标时，算法将自动排除掉禁忌表Tabu中的点，在剩余坐标点中继续随机生成。当第二个井位坐标产生后，根据步骤1)的方法，继续扩充禁忌表Tabu；

3)重复步骤2)直到井位数为n。

以上步骤是禁忌表策略在初始种群生成时的应用，在种群进化时，该步骤同样适用，只不过由于算法需要根据适应度函数(目标函数)朝着求解的最优的方向进行，故步骤2)中的坐标点不再是随机生成，而是改为在进化更新后的坐标向量中，以第一坐标点为基准建立禁忌表，其余不符合约束条件的坐标在禁忌表以外的坐标点中选取最近的坐标进行替换。

本文利用改进后的量子遗传算法优化井位及数量的流程如图2所示。

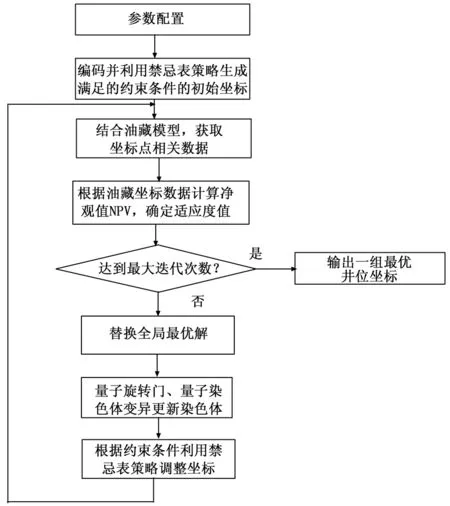
图2 改进后算法流程图

1)算法中的参数设置包括油藏参数、算法参数设置。油藏参数主要包括油藏数据以及预设油井个数，油藏数据主要在目标函数的计算中使用，通过计算得数来判断井位坐标的优劣，预设油井个数则决定了算法生成初始坐标的个数；算法参数则主要决定了算法迭代次数与运算速度。

2)针对本问题是以NPV最大为目的进行优化，故算法中的全局最优解即为特定井数下一组NPV最大的井位坐标，算法每经过一次迭代都会通过NPV对当代种群进行评价，并选取其中NPV最大的解与历史全局最优解进行比较，选择其中较大的值作为当前全局最优解，不断循环，直到算法停止迭代时输出该解。

3 仿真实验与结果分析

3.1 实验参数设置

本文在算法运行时涉及到的计算参数有以下几种：

生产年限T：T= 5 (年)；

孔隙度φ：φ=[12.0156+2.2613logk(x,y)]/100

压缩系数Cp：Cp=φ×10-3+10-6(MPa-1)；

油层厚度h：h= 50(米)；

油层粘度μ：μ= 5.0(mPa·s)；

生产压差ΔP：ΔP=10(MPa)；

泄油半径R：R=100(m)

主要经济参数有：建设成本Pinit100万元；操作成本Pop200万元；维护成本Pre50万元；原油价格Po500元/m3；折现率η=0.1；通货膨胀率δ=0.04。

主要算法参数有：种群大小100；进化代数100。

3.2 实验结果及分析

本文在分别在拟定的生产井数n={1 2 3…10}的条件下，对模型进行了多次运算，分别计算出了不同的拟定井数下，5年时间后的NPV值以及最佳井位坐标。其中不同井数与其对应的最优NPV值如图2所示。根据图2曲线可以看出，针对该油藏模型通过算法优化后的合理井数为5口。当井数小于5时，NPV随着井数的增加而增加；当井数超过5口时，NPV随着井数的增加而减小，这是因为随着井数的增加，虽然油田的累积产量会增加但其增长幅度小于成本的增长幅度，因此会导致NPV的减小。

部分井数最优坐标如图3所示。可以看出最优的布井位置与油田渗透率的分布有密切联系，渗透率大的坐标区域内井数较多，而渗透率小的坐标区域内井数很少。通过图4(a)、(b)、(c)、(d)的对比可以发现，在优化布井时渗透率高的坐标点总是被优先考虑，例如，在坐标(11,16)附近的区域内点，无论总井数多少均会被选中。同时也可以发现，当井数较多时优化后的井位较为分散，这是由于本文所研究的油藏模型的非均质程度较大，渗透率分布不均匀。对于该种地质区块，算法优化布井比常规布井更具优势，下面将具体说明。

图3 井数-NPV关系曲线

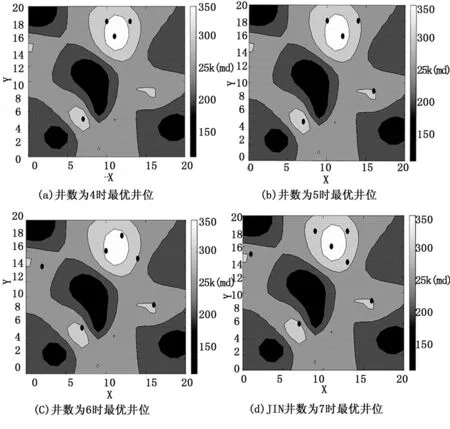
图4 部分井数对应的最优井位

为了进一步说明算法优化布井的优势，本文将传统布井方式与优化后的布井方式进行了对比，以井数为5、6为例，传统布井方式如图4所示。

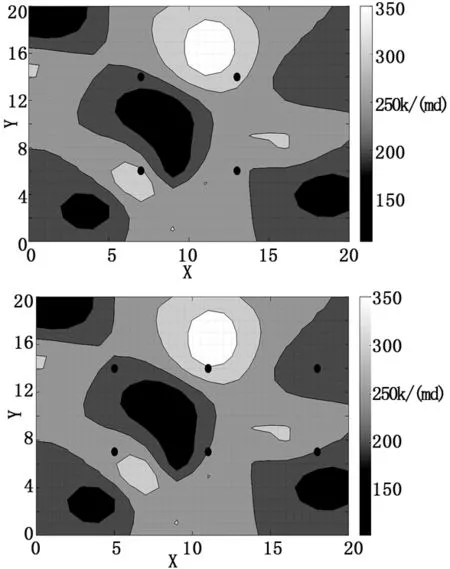
图5 传统布井方法

通过优化前后的NPV来说明优化效果，NVP的计算年限同样为5年，在不同预设井数下，传统布井方式的NPV与优化后的NPV如表1所示。

由表1可以看出，使用优化布井在五年内所获得的收益在任何井数上均优于常规布井，尤其在最佳布井数(井数为5)时，增幅达到最大。同时，从常规布井的NPV值随井数变化可以看出，当井数达到6口时，继续开井反而会使NPV值降低，这从说明了另一方面说明了无论采取任何布井方式，合理规划井数都是一定年限内取得最佳收益的重要途径。

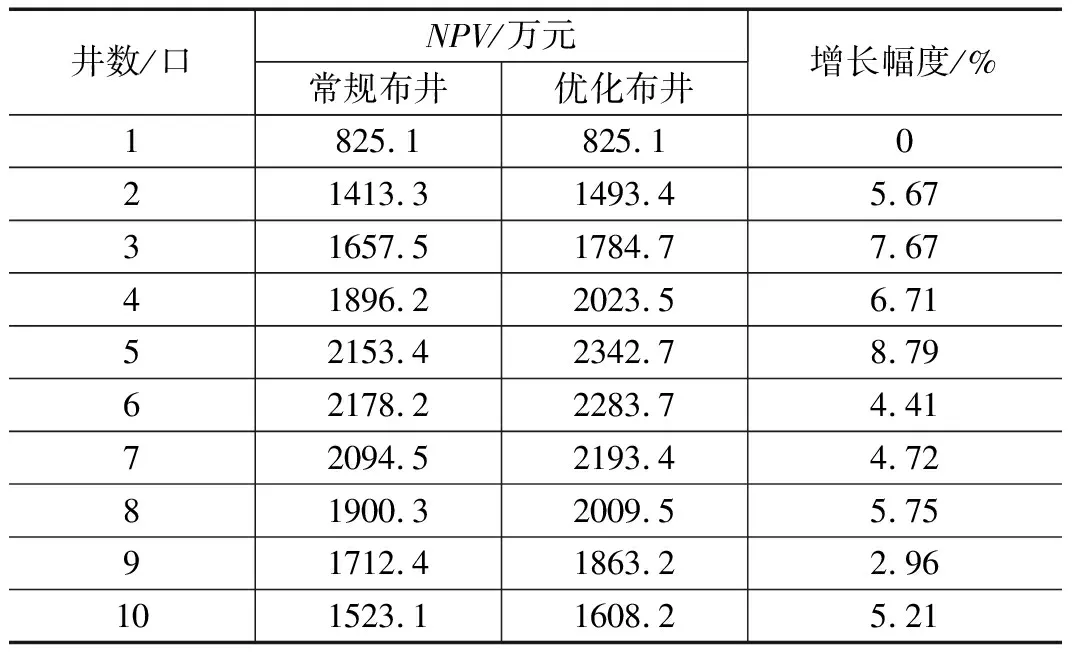
表1 常规布井与优化布井NPV比较

4 结束语

本文研究将改进量子遗传算法应用到油田井位数量及位置优化中，其中目标函数为净现值。并通过数值模拟的方法在Matlab上建立仿真模型进行实验，通过优化实验可知，基于量子遗传算法的井位及数量优化能在知晓油藏模型的前提下确定油田最优井位及数量，不仅克服了常规布井对经验的依赖性，还通过优化NPV前后的NPV值体现了优化方案良好的经济性。

由于本次研究是通过模拟油藏模型来验证优化方案的可行性，为了简化问题的数学描述，本次研究的约束条件仅为井间距离，但在实际应用中，许多因素例如：地质条件、驱动方式、流体特殊特性等等都会对油田的NPV值造成影响。因此进一步结合实际情况，提升优化方案的泛化性是本次研究的主要后继工作，需要继续深入研究。