基于协同优化算法的流速仪检定系统设计
, ,,,
(1.国防科技大学 气象海洋学院,南京 211101; 2.西北核技术研究所,西安 710024; 3.中船重工鹏力(南京)大气海洋信息系统有限公司,南京 211106; 4.中国人民解放军第94116部队,新疆 和田 848000)
0 引言
在水文观测领域,流速是主要的观测参数之一。实时准确的流速测量数据有助于了解水资源的分布规律,为水资源的开发和利用等提供重要的科学依据,因此准确测量流速已经成为气象、水文等领域的研究重点[1-2]。为保证流速测量结果的准确一致,需要对各种类型的流速测量设备建立完善的计量检定体系。国家标准GB/T 21699-2008《直线明槽中的转子式流速仪检定/校准方法》规定的流速仪检定设备为直线静水水槽和检定车[3],然而该设备体积庞大,建造及维护成本高,且可用设备数量较少,导致目前转子式流速仪的计量检定工作效率较低且费用较高。基于上述原因,本文提出研制一套基于环形水槽的小型轻便式流速标准装置,并运用多学科协同优化方法求解系统的最优化设计方案。
多学科设计优化(Multidisciplinary Design Optimization,MDO)是一种运用各学科间互相作用的协同机制来实现复杂系统最优化设计的方法论[4-5]。与传统的串行设计方法相比,MDO算法充分考虑了各学科间的耦合关系,利用多目标策略和计算机辅助设计等手段实现了各子学科的并行优化,从而有效提高了设计效率和质量[6]。在求解MDO问题的众多方法中,协同优化(Collaborative Optimization,CO)算法具有良好的学科独立性和并行优化效果,适用于多学科交叉耦合的复杂系统设计,在最优化问题中得到广泛应用[7-8]。
在CO算法求解过程中,系统级优化采用的一致性等式约束过于理想化,往往会导致优化问题不满足Kuhn-Tucher条件[9],且限制了系统级优化计算的自由度,在求解中易出现迭代过程无法收敛或陷入局部最优等问题[10]。针对上述缺陷,已有学者从不同角度对CO算法进行了研究,并在一定程度上改善了算法的计算能力。一方面,对系统级约束条件的数学表达形式进行改进,文献[11]引入罚函数概念将系统级优化转化为无约束优化问题;文献[12]利用松弛因子法将系统级一致性等式约束转化为不等式约束;文献[13]提出运用响应面法对系统级的一致性等式约束进行近似处理。另一方面,用智能算法代替传统的梯度算法,提出了基于粒子群算法、遗传算法、支持向量机、模拟退火等算法的协同优化方法[14-16]。智能算法具有较强的全局寻优能力,可有效避免优化过程无法收敛或陷入局部最优等问题。
基于上述改进方法,本文结合动态松弛因子法和遗传算法给出了一种改进CO算法的数学模型,并将其应用于流速仪检定系统的优化设计中。流速仪检定系统的设计涵盖了流体力学、伺服控制等多个学科,各子学科设计变量交叉耦合、密切关联,采用协同优化方法有助于获得系统的最优化设计方案。本文首先讲述了流速仪检定系统的设计要求,并运用SolidWorks三维建模软件建立了系统的概念模型;然后运用改进CO算法建立了多学科优化模型,得到了系统的最优化设计参数,并运用计算机仿真等方法验证了优化结果的可行性。
1 协同优化算法
1.1 CO算法的数学描述
CO算法将复杂的MDO问题分解为一个系统级优化问题和若干个并行的学科级优化问题。在优化过程中,系统级根据系统约束条件协调各子学科优化结果的一致性差异,并为学科级设计变量提供优化目标;各子学科根据系统级提供的优化目标进行独立并行优化,在满足学科级约束条件的前提下,使子学科设计变量最优解与系统级优化目标的差值达到最小。通过系统级与学科级之间的多次优化迭代,最终可获得满足学科间一致性约束的设计变量最优解[17-18]。
根据上述算法原理,CO算法的数学模型可表示如下:
1)系统级优化数学模型:
minf=f(z)
(1)
式中,f(z)为系统级优化目标函数,Ji(z)为子学科i的一致性约束条件;zij表示系统级分配给第i个子学科第j个设计变量的优化目标,pij表示第i个子学科中第j个设计变量的最优解;n为参与优化的子学科个数,m为第i个子学科中耦合变量的个数。
2)学科级优化数学模型:
s.t.hi(x)≤0
gi(x)=0
(2)
式中,Ji(x)为子学科i的优化目标函数,hi为子学科i的不等式约束,gi为子学科i的等式约束;xij表示第i个子学科的第j个设计变量。
根据算法原理和数学模型,可建立CO算法的求解流程如图1所示。
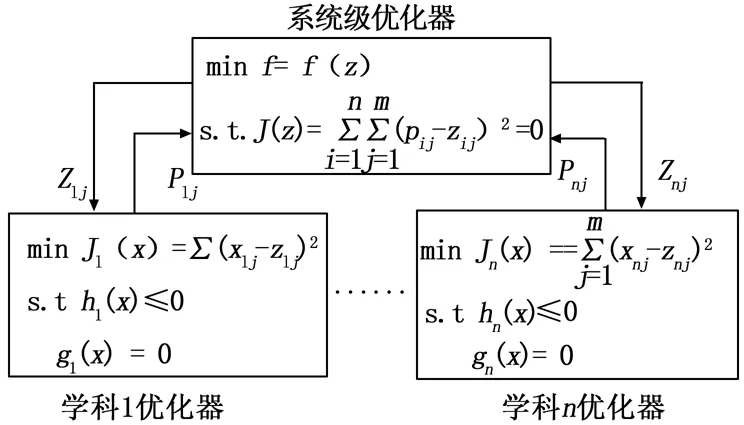
图1 协同优化算法的求解流程
1.2 基于动态松弛因子的CO算法
标准CO算法采用的系统级一致性等式约束过于理想化,在工程应用中易出现收敛速度慢或系统级可行域不存在等问题。松弛因子的引入,可将系统级一致性等式约束转化为不等式约束,虽然增强了算法的鲁棒性和收敛速度,但也导致了新的问题:松弛因子的取值对系统级优化性能的影响较大,对于不同的MDO问题,难以找到普适的松弛因子取值方法[19];算法的优化迭代过程对松弛因子的取值较为敏感,定值松弛因子无法确保每一步优化迭代中系统级可行域的存在[20]。为解决上述问题,文献[21]根据学科间的不一致性信息建立了动态松弛因子模型,为系统级优化提供了动态约束范围。然而,该模型中松弛因子的选择仅限于两个子学科之间的不一致信息,若一个MDO问题涉及多个子学科,需首先确定各子学科间不一致性的最大值,增加了优化过程的计算量。本文中运用子学科设计变量最优解和系统级设计变量优化目标之间的不一致信息定义动态松弛因子ε,有效避免了上述问题。
(3)
ε=λ·Δ0.5<λ<1
(4)
式中,pijk表示第k次迭代时第i个子学科中第j个设计变量的最优解;zijk表示第k次迭代时系统级分配给第i个子学科第j个设计变量的优化目标;Δ为子学科设计变量最优解和系统级设计变量优化目标之间的不一致信息;λ为搜索范围因子。
动态松弛因子的引入,将系统级一致性等式约束转化为不等式约束,此时系统级优化的数学模型可表示为:
minf=f(z)
(5)
1.3 遗传算法在MDO问题中的应用
遗传算法(Genetic Algorithm,GA)是一种基于生物进化和自然选择机制的随机性全局寻优算法[22-23]。与传统寻优方法相比,遗传算法以适应度函数为目标,通过对群体中所有个体进行遗传操作实现个体的结构重组,在迭代过程中搜索种群的最优个体。
遗传算法通过概率变化规则来确定其搜索方向,具有强大的并行计算能力,可同时对搜索空间中的多个个体进行分析,具有较强的鲁棒性,可有效降低收敛过程陷入局部最优的概率[24-25]。并且,遗传算法不受优化准则、模型结构、梯度信息等因素的制约,仅仅依赖于概率规则指引下的全局并行寻优机制[26]。作为一种求解优化问题的通用框架,已广泛应用于组合优化、人工智能、机器学习等领域。本文中运用遗传算法求解各学科设计变量的最优解。
2 系统优化模型建立
2.1 概念模型
运用SolidWorks软件建立了如图2所示的检定装置概念模型,其主要结构包括环形水槽、伺服系统和测控系统等。其中,实验所需的静水环境由环形水槽提供;伺服系统作为装置的动力输出,可带动被检仪器在环形水槽中以设定的速度做圆周运动;测控系统用于向伺服系统发送控制指令并读取装置运行的相关数据。

图2 流速仪检定系统概念模型
2.2 设计要求
依据小型轻便的设计理念和被检仪器的测量范围,设定系统总重量(除环形水槽及其附属部件)不超过150 kg,检定速度范围为0.1~4.5 m/s。伺服系统带动被检仪器环绕水槽转动,加速至目标检定速度后保持匀速运动,在转动一圈过程中完成一个速度点的检定。在最高检定速度下,要求被检仪器在匀速段的运动时间不小于3.5 s。
2.3 协同优化设计模型
在该系统中,环形水槽几何参数、伺服系统特征参数等变量相互耦合、密切关联。综合分析各学科优化目标、约束条件和设计变量的耦合关系,可将检定系统的多学科设计优化问题分解为流体力学、伺服控制和材料科学3个子学科。
2.3.1 环形水槽几何参数优化模型
为减小实验装置的体积、重量、建造和维护成本,满足其小型轻便的设计要求,装置采用环形水槽取代传统的直线静水水槽,并在水槽中设置隔板,避免被检仪器启动时造成的流体扰动破坏其后侧流场的稳定性,其概念模型见图2。
根据系统设计要求,建立环形水槽几何参数的优化模型如下:
1)设计变量:
X1=[x11,x12,x13]=[r,W,D]
(6)
式中,r为被检仪器转动半径,W为储水区宽度,D为储水深度。
2)目标函数:
minF1(x)=ω1f1(x)+ω2f2(x)
(7)
式中,f1(x)为储水区横截面积函数,f2(x)为水槽底面积函数,ω1、ω2为加权系数。
3)约束条件:
在环形水槽几何参数的设计优化中,需考虑阻塞效应[27]、侧壁效应[28]、浅水效应[28]等影响因素,根据上述因素可得环形水槽几何参数优化模型的约束条件如下:
(8)
式中,R为水槽外环半径;Lf,Wf,Sf分别为被检仪器长度、宽度以及来流方向的横截面积,vmax为最大检定流速,α为伺服系统角加速度。
2.3.2 伺服系统特征参数优化模型
伺服系统主要包括伺服电机、减速机构、传动臂等,其概念模型如图3所示。决定伺服系统运动特性的参数有伺服电机额定功率、额定力矩、额定转速、传动机构减速比等。为满足系统的设计要求,需对上述参数进行协同优化,并将优化结果作为伺服系统核心部件选型的依据。
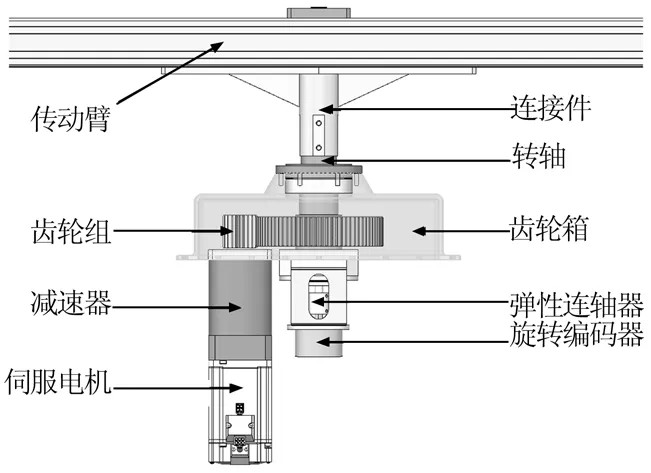
图3 伺服系统概念模型
建立伺服系统运动特性优化模型如下:
1)设计变量:
X2=[x21,x22,x23,x24,x25]=[Pe,ne,Me,I,α]
(9)
式中,Pe,ne,Me分别为伺服电机的额定功率、额定转速和额定力矩,I为传动机构减速比。
2)目标函数:
(10)
3)约束条件:
根据机械传动的力学定律和绕流阻力的求解方法,可得伺服系统的数学模型,并据此建立伺服系统优化模型的约束条件如下:
(11)
式中,MJ为负载惯性力矩,Jd为电机转子的转动惯量,Jz为负载总转动惯量,Mf为负载阻力力矩,η为机械传动效率,ωmax为系统最大角速度,I1为减速器提供的减速比,I2为齿轮组减速比。
2.3.3 检定系统重量优化模型
检定系统框架结构的概念模型如图4所示。为满足系统的重量设计目标,需对框架结构高度、传动臂臂长、承载平台面积、材料密度及其余部件总重量等参数进行优化。
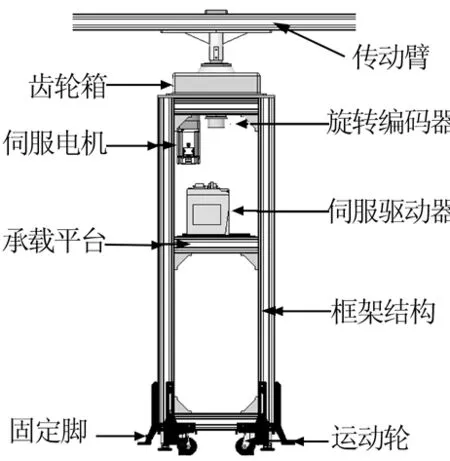
图4 框架结构概念模型
检定系统重量优化模型如下:
1)设计变量:
X3=[x31,x32,x33,x34,x35,x36]=
[h,l,a,b,ρm,m]
(12)
式中,h为实验装置高度,l为传动臂臂长,a、b为承载平台的长度、宽度,ρm为材料密度,m为其余部件总重量。
2)目标函数:
房丙午 男,1974年生于安徽枞阳.现为南京航空航天大学计算机科学与技术学院博士研究生,副教授.主要研究方向软件工程、软件系统安全性分析.
minF3(x)=ω3f3(x)+ω4f4(x)+ω5f5(x)
(13)
式中,f3(x)为框架结构重量函数,f4(x)为传动臂重量函数,f5(x)为其余部件重量函数,ω3、ω4、ω5为加权系数。
3)约束条件:
(14)
式中,mh为框架结构重量,ml为传动臂重量,s为材料横截面积,δ为承载板厚度,ρ1为承载板材料密度,mi分别为固定脚及运动轮、伺服电机及适配驱动器、伺服减速器、齿轮及轴承组件、旋转编码器、连接件的重量,hi分别为固定脚及运动轮、框架结构、齿轮及轴承组件的高度。
2.3.4 系统级优化模型
在该MDO问题中,被检仪器转动半径r和伺服系统角加速度α两变量存在子学科间耦合关系,故需要通过系统级优化协调两学科间共享变量的一致性差异。
1)设计变量:
Z=[z1,z2]=[r,α]
(15)
(16)
3)一致性约束:
(17)
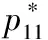
3 优化求解及结果验证
采用基于动态松弛因子的CO算法求解流速仪检定系统的MDO问题,迭代寻优过程选用遗传算法,采用规格化加权方法求解各学科目标函数的加权系数,各子学科设计参数的寻优结果及验证方法如下。
3.1 环形水槽几何参数优化结果
根据上述约束条件和目标函数,编写优化模型的GA程序,设定种群大小为50,最大迭代次数为50次,交叉率0.85,变异率0.1。水槽几何参数的优化结果如表1所示,优化迭代过程中适应度函数值的变化曲线如图5所示。

表1 环形水槽几何参数优化结果
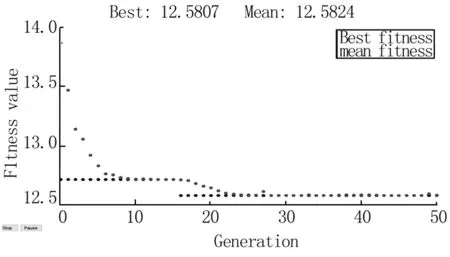
图5 迭代过程中适应度函数值变化曲线
根据优化结果,设定环形水槽的几何参数如下:储水区宽度0.8 m,被检仪器转动半径2.8 m,内环半径2.4 m,外环半径3.2 m,储水深度1.0 m。根据上述几何参数,验证阻塞效应、侧壁效应、浅水效应等影响因素,结果如下:水槽与流速传感器横截面积的比值约为630,满足阻塞效应要求;水槽储水深度大于流速传感器长度,满足浅水效应要求;水槽与流速传感器宽度的比值为20,满足侧壁效应要求。
3.2 伺服系统特征参数优化结果
伺服系统的优化目标为被检仪器加速距离最短,即系统提供的角加速度最大。为此,需对伺服系统力矩、减速比等参数进行优化,并根据优化结果确定伺服执行元件的选型。为获得最优的设备选型方案,在算法求解过程中适当放宽了该子学科优化模型的约束和收敛条件,以合理性分布区间的方式给出优化模型的求解结果,如图6所示。

图6 伺服系统参数优化结果分布区间
在伺服系统元件选型时,为获得较高的性价比,在满足性能需求的前提下,应尽量选择力矩较小的伺服电机,并根据其转速特性,确定系统的减速比。根据图6给出的优化区间,选定松下A5Ⅱ MHMJ082G1C型伺服电机作为伺服系统的动力元件,其基本参数如表2所示。并根据该型号伺服电机的转速参数,设定传动机构总减速比I=160,减速器提供的减速比I1=40,齿轮组提供的减速比I2=4。
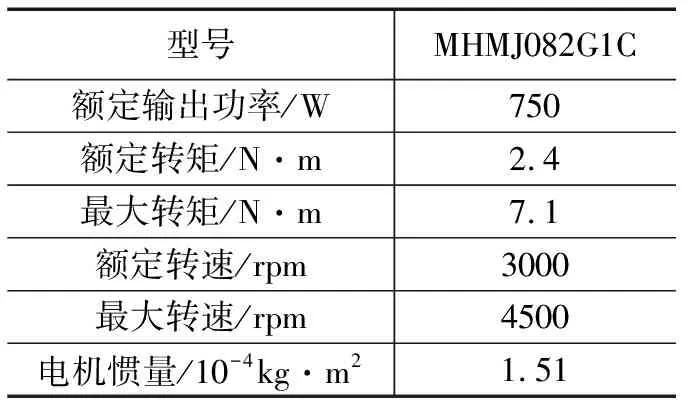
表2 松下A5Ⅱ伺服电机技术参数
为验证伺服系统执行元件选型的合理性,采用Simulink动态仿真平台对伺服系统的运动特性进行验证。建立伺服系统的动态特性微分方程和如图7所示的Simulink仿真框图,在检定速度范围内选取6个检定点:0.1 m/s、1.0 m/s、2.0 m/s、3.0 m/s、4.0 m/s、4.5 m/s,通过仿真模型研究其动态特性,可得加速时间、加速距离、匀速运动时间等参数如表3所示。结果表明,在最高检定速度下,被检仪器的匀速运动时间大于3.5 s,满足设计要求。
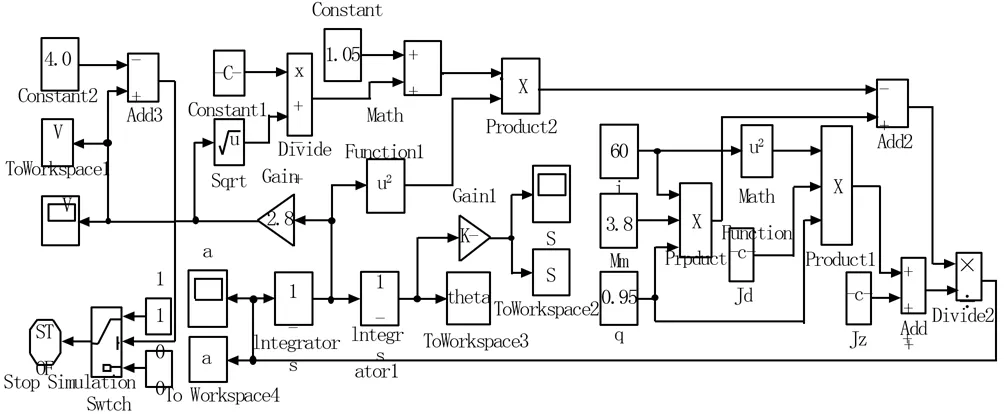
图7 伺服系统动态特性仿真框图

检定速度/(m/s)0.11.02.03.04.04.5加速时间/s0.0050.0510.1020.1530.2040.230加速距离/m0.00030.0250.1020.2290.4090.518匀速时间/s175.917.68.75.84.33.8
3.3 系统重量优化结果
目前传动机构中通常采用钢材和铝合金等材料,几种材料的基本参数如表4所示。综合考虑材料密度、成本、力学特性等因素,选用铝合金6063-T5作为检定系统框架结构的加工型材。

表4 几种材料的特性参数
将选定的材料参数代入优化模型,可得如表5所示的系统重量优化参数。根据优化结果修改检定系统概念模型的几何参数,运用SolidWorks中的称重工具测得系统总重量(除环形水槽及其附属部件)约为84.4 kg,满足重量设计要求。

表5 系统重量优化结果
4 结论
本文运用改进的协同优化算法,完成了流速仪检定系统的最优化设计,结论如下:
1)CO算法的两级优化机制充分考虑了多学科复杂系统中设计变量的耦合关系,有效提高了设计效率和质量。本文中建立了流速仪检定系统的协同优化模型,获得了各学科设计变量的最优解,经验证可知优化结果满足系统设计要求。
2)动态松弛因子的引入,提高了算法的自由度和适应性,确保了每一步优化迭代计算中系统级可行域的存在;遗传算法具有强大的并行计算能力,其基于概率规则的全局寻优机制有效降低了迭代过程陷入局部最优的可能性。
3)在MDO问题中,协同优化应作为指导工程设计的宏观思想而不仅仅是优化结果的求解工具。设计方案的优化过程不应该束缚于CO算法的数学框架和计算结果,而应该结合实际问题灵活运用协同优化方法。在流速仪检定系统的MDO问题中,伺服控制子学科的优化结果以设计变量可行区间的方式呈现,由此可获得多样化选型方案。在系统重量优化模型中,首先依据材料特性、成本、通用性等因素完成了材料选型,并据此得到了框架结构几何参数的最优解,经验证得优化方案满足设计要求。
4)作为检定标准装置,应着重分析系统的测量准确度、扩展不确定度等参数。在本系统中,计量检定子学科与其他学科不存在耦合关系,故未将其列入协同优化模型中。标准器选择、测量误差分析、不确定度评定等内容将另文阐述。

