电磁航天器编队悬停鲁棒协同控制方法

张亚博， 师鹏，*， 张皓， 赵育善

(1. 北京航空航天大学 宇航学院, 北京 100083； 2. 中国科学院空间应用工程与技术中心中国科学院太空应用重点实验室， 北京 100094)

编队悬停是指空间中的多个伴随航天器在控制力或自然力的作用下，相对参考航天器或其他自然天体保持相对静止的状态。编队悬停技术在航天器在轨服务、深空探测、航天器跟踪监视等领域有着广泛的应用[1-3]。

航天器悬停编队的实现依赖于准确的轨道和姿态控制。在近距离悬停时，传统基于冲量原理的推力器会造成羽流污染，某些任务甚至会严格限制目标与悬停航天器连线方向的点火[4]；再者编队中成员航天器悬停轨道通常具有强非开普勒性，要求推力器长时间工作[5]，必然导致传统航天器编队寿命有限。因此利用库仑力[6]、洛伦兹力[7]和电磁力[8]等非接触力实现航天器无工质编队的控制受到了众多学者的关注。相比于星间库仑力、洛伦兹力，通电电磁线圈间能够产生任意方向的电磁力，可以实现更多的控制自由度，本文选择星间电磁相互作用来实现航天器编队的控制。电磁航天器通过改变其上安装的3个正交电磁线圈的电流以改变航天器受到的电磁作用，进而实现航天器编队的相对轨道控制[9]。

通过引入电磁相互作用之后较好地解决了传统推力器存在的问题，但电磁作用固有的非线性、相互性以及空间环境的不确定干扰决定了电磁航天器编队控制具有强非线性、强耦合性以及不确定性的特点[10]。此外，电磁力是系统内力，无法实现编队质心的机动。这些因素对控制的设计提出了更高的要求。

针对电磁航天器编队的动力学与控制问题，国内外学者进行了丰富的研究。就双电磁航天器编队控制，Elias等[11]引入双电磁航天器编队动力学非线性模型并对其进行了线化，分析了线性模型的闭环稳定性和可控性，设计了最优线性反馈控制律。黄涣等[12]基于Kane方法建立了电磁航天器六自由度耦合非线性动力学模型，分析了3种平衡态构型的控制需求，并设计了线性二次型调节器(LQR)控制器。徐增文等[13]针对双星电磁航天器构型保持设计了自适应控制律，并给出了双星磁矩配置解析表达式。邵龙飞等[14]将双星编队运动规划问题转化为标准优化问题进行了求解，并指出多电磁航天器的编队控制可以转化为分阶段的双电磁航天器控制。Kwon等[15]用双星地面实验验证了利用超导线圈产生电磁力进而进行位置保持和轨道跟踪的可行性。

对于多电磁航天器编队控制，Ahsun和Miller[16]给出了编队相对运动二维动力学模型，并分别基于人工势函数法和最优控制方法研究了电磁航天器编队的构型保持问题。Miller等[17]基于近地轨道动力学模型，采用非线性自适应控制方法研究了电磁航天器编队的构型保持和重构问题，并提出了通过优化配置磁矩的方案。胡敏等[18]分析了地磁场对近地轨道电磁编队的影响，建立了高精度相对运动动力学模型，在此基础上提出了一种非线性反馈控制方法。Zeng和Hu[19]在动力学模型存在不确定性和外部摄动的情况下，设计了电磁航天器编队轨道跟踪的线性终端滑模控制。Zhang等[20]建立了六自由度电磁航天器动力学模型，给出了航天器轨道姿态控制的自适应终端滑模控制。

尽管以上研究较好地解决了电磁航天器编队的相对构型保持和轨道姿态跟踪问题，但文献中采用的动力学模型大多数只考虑了外部摄动的不确定性，而未考虑动力学模型的内部不确定性和参数摄动，在实际的任务中该参数摄动是不可避免的。再者，当参考轨道是椭圆时，系统呈现动态时变特性，文献中设计的控制律均需要参考轨道实时的准确信息，获取这些信息一些情况下是十分困难甚至是不可能的。此外，文献中设计的控制律并未考虑编队成员航天器之间的信息交互，导致编队的协同能力较差并产生冗余控制。

考虑到上述问题，本文针对电磁航天器编队近地轨道悬停控制，提出了一种在缺少参考轨道准确信息时的协同控制方法。首先，用TH方程描述航天器间的相对运动，选择与参考轨道同周期的圆轨道作为标称轨道，将参考轨道相对于标称轨道的偏差、地球非球形引力、大气阻力以及其他天体引力等参数单独归类，视其为不确定量，构成不确定系统。然后，针对动力学方程存在内部和外部不确定性，通过引入滑模控制理论和一致性理论，就电磁航天器编队悬停的目标设计了鲁棒协同控制律。最后，考虑到能量消耗最优和均衡以及轨道姿态解耦的问题，给出了通过优化进行磁矩配置的方案，并进行了数值仿真验证。

1 电磁航天器编队动力学建模

1.1 电磁远场作用模型

电磁航天器通过其上安装的3个正交电磁线圈产生电磁相互作用，如图1所示。图中i1、i2为线圈电流；a1、a2为线圈半径；dl1、dl2为线圈长度微元；d为线圈微元间的距离；s为线圈2的微元于线圈1的中心的距离。可以采用毕奥-萨伐尔定律精确计算2个通电线圈之间的电磁力和电磁力矩，设线圈2位于线圈1的电磁场中，对线圈2上的电流微元在线圈1的电磁场中进行积分，即可求得线圈2受到线圈1的电磁力F2和力矩T2分别为

(1)

(2)

式中：μ0=4π×10-7N/A2为真空磁导率。

式(1)、式(2)形式复杂，不易在工程中直接应用。研究发现[21]，2个线圈之间的距离大于5倍的线圈半径时，将线圈视为偶极子得到的远场电磁力模型误差在10%内，能够基本满足精度需求。远场电磁力模型如图2所示。该模型将线圈电磁场视为偶极子，其大小和方向用磁矩描述，磁矩的求解公式为

μ=nISl

(3)

式中：n为线圈的匝数；I为电流值；S为线圈的面积；l为载流平面法线方向单位向量，服从右手定则。

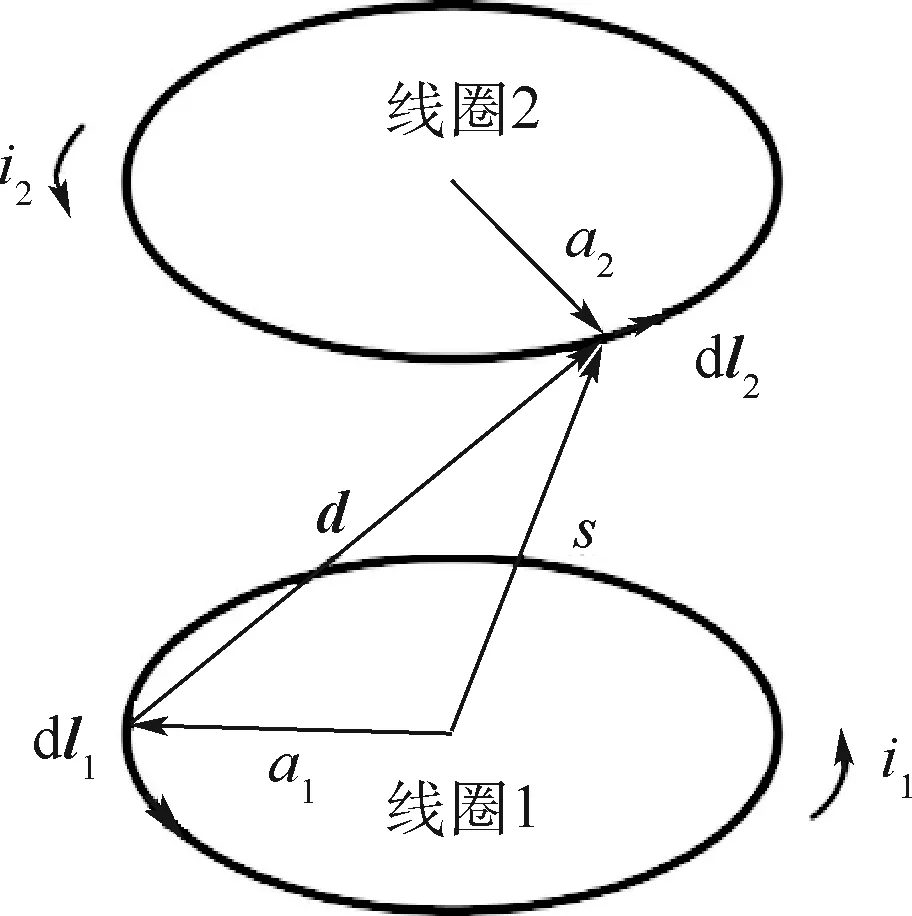
图1 电磁线圈相互作用示意图Fig.1 Schematic diagram of electromagnetic coil interaction

图2 磁偶极子相互作用示意图Fig.2 Schematic diagram of magnetic dipole interaction

远场模型下，两线圈之间的电磁力和电磁力矩可以分别为

(4)

(5)

由式(4)、式(5)可以看出，远场模型下电磁力是线圈磁矩和线圈之间距离的强非线性函数，这使得在电磁力已知的情况下，求解磁矩变得较为困难。从式(4)和式(5)也可以看出，电磁力和电磁力矩是耦合产生的，在多航天器编队(航天器数量大于2的编队)中，这种耦合性将导致设计控制律时产生控制欠驱动问题。本文设计控制律时，采用轨道优先策略对其进行解耦，将电磁力矩考虑为干扰因素，其可以用反动量轮或力矩陀螺进行消除。本文研究重点是电磁航天器编队的轨道悬停控制，因此不考虑其姿态控制，并假设航天器的姿态已经调整到了期望的状态。

1.2 相对运动动力学模型

为描述航天器之间的相对运动，首先引入2个参考坐标系，即地心惯性坐标系Si和参考轨道坐标系SO′。如图3所示，地心惯性坐标系坐标原点位于地球中心，X轴位于赤道平面，指向春分点方向，Z轴垂直于赤道平面，指向北极为正，Y轴与X轴、Z轴构成右手系。参考轨道坐标系坐标原点位于参考航天器质心，x轴沿径向，从地球中心指向参考航天器质心，y轴在轨道平面内与x轴垂直，指向参考航天器前进方向，z轴与x轴、y轴构成右手坐标系。

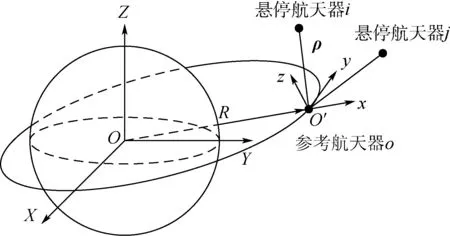
图3 航天器编队悬停参考系Fig.3 Spacecraft formation hovering coordinate system

假设对参考航天器不施加控制且编队中成员航天器之间的距离远小于航天器质心到地心的距离，则在参考轨道坐标系下，悬停编队中的成员航天器相对参考航天器的线性相对运动动力学方程为

(6)

式中：下标i=1,2,…,N为悬停编队中航天器的编号；ρi=[xiyizi]T为悬停航天器i在参考轨道坐标系SO′中的位置；umhi为悬停航天器i受到的远场电磁力；udhi为悬停航天器i受到的外部摄动，包括电磁力建模误差、气动力、太阳光压以及地磁场和其他天体引力引起的摄动；udo参考航天器受到的外部摄动，包括气动力、太阳光压摄动以及其他天体引力。式(6)中的各系数矩阵为

(7)

(8)

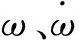
2 电磁航天器编队悬停控制方法

2.1 鲁棒协同控制律设计

滑模控制能够有效克服系统的不确定性，对干扰和未建模动态具有很强的鲁棒性，且具有响应迅速、物理实现简单等优点。本文将以滑模控制方法为基础实现航天器的悬停。

对于一般的椭圆参考轨道，式(6)表示的相对运动动力学模型是一个系数时变的微分方程，式中变化的参数都与参考轨道相关，若按式(6)设计控制律将需要获得参考轨道实时的准确参数，带来很多的不便。本文拟将一个与参考轨道同周期的圆轨道作为基准，将参考轨道和标称圆轨道的偏差、地球非球形摄动以及其他各种摄动单独归类，作为不确定量进行处理，由此得到的动力学方程为

(9)

式中：udi=udhi-udo为悬停航天器相对参考航天器的外部不确定量；ΔD为椭圆轨道相对于圆轨道的偏差以及动力学方程的参数摄动；ΔK为参考轨道相对于圆轨道的偏差、地球非球形引力摄动以及动力学方程的参数摄动。与椭圆轨道同周期的圆轨道的半径为椭圆的半长轴a，因此矩阵Dc、Kc的值为

(10)

(11)

不确定矩阵可表示为

(12)

(13)

|udi|≤fi(x,t)fi(x,t)≥0

(14)

式中：Ei、Fj为已知矩阵，存在参数摄动的位置元素为1，其余元素为0；αi、βj为不确定矩阵ΔD、ΔK对应位置的摄动参数；ai、bj分别为αi、βj模的上界；f(x,t)为外部不确定量udi模的上界;k、h分别为矩阵ΔD、ΔK不为零的元素的个数。

小偏心率参考轨道本质是时变的，动力学模型中存在真近点角，涉及到实时进行开普勒方程的求解，同此还涉及到线性时变系统的控制，在设计控制律时存在着一定的难度。这里通过用一个同周期的圆参考轨道代替这个小偏心率椭圆，使得系统由非定常变成定常，分析设计比较方便。这么一来，就会出现一个小周期项的动力学偏差，这里把它也作为不确定性进行处理。另外，由于文中把时变的部分都当作了小扰动，那么即使对参考卫星的建模存在一定误差，上面设计的控制仍然可以保证不错的效果。因此，基于式(9)的模型设计的控制律将具有更强的鲁棒性。

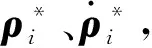
选取滑动面为

(15)

式中：Λ=diag{λr}，λr>0，r=1,2,3，显然滑动面上的状态运动是稳定的。接下来设计到达运动，对式(15)的滑动面函数求导，得

(16)

(17)

选择到达控制律为

(18)

式中：Hi和εi为对角元素均为正的对角矩阵，且Hi，εi∈R3×3。为了消除滑动运动在滑模面上的抖颤，在此处选择饱和函数sat(x)代替符号函数：

(19)

式中：φ为饱和函数边界层厚度。对比式(17)、式(18)得到等效控制为

(20)

式(20)控制中存在不确定参数，无法直接使用，为消去不确定参数，首先任选2个向量z1i、z2i，构造式(21)作为实际控制：

umhi=-Hisi-εi·sat(si)+

(21)

为确定z1i、z2i，将式(21)代入式(17)中得

(22)

又滑模控制到达条件为

(23)

将式(22)代入式(23)之后写成分量形式得

(24)

式中：上标r=1,2,3为向量的第r个分量；vr(*)为矩阵(*)的第r行，若取z1i、z2i为式(25)、式(26)。将式(25)、式(26)代入式(24)，比较各项大小，消去不确定项，可使得到达条件式(23)得到满足。

(25)

(26)

式(21)～式(26)构成航天器编队悬停的控制律，该控制律已经能够实现航天器编队的悬停任务，且由于动力学模型中考虑了航天器可能受到的所有的误差，同时给出了模型误差的上界。因此上面给出的控制对不确定干扰具有较强的鲁棒性，但该控制律只考虑了编队中成员航天器自身的位置和速度偏差信息，没有用到其他航天器的状态信息，从编队系统层面上来看，所设计的控制律只能够达到局部的良好性能，从全局视角审视，存在控制的浪费，因此对该控制律进行改进，以利用航天器之间的信息交换实现全局协同。

为了清晰地描述航天器编队中成员航天器之间的关系，在此引入图论的相关概念。一个加权无向图G(V,E,A)由节点集V={1,2,…,N}，边集E⊆V×V和加权邻接矩阵A=a[ij]∈R组成。节点表示编队中的成员航天器，边表示编队中成员航天器之间的通信关系，邻接矩阵表示编队中成员航天器的通信性能。无向图中若两航天器i、j之间可以通信，则边(i,j)∈E、(j,i)∈E且aij=aji>0，否则aij=0。一般认为航天器和自身不存在通信，即aii=0。如果图中的任何2个节点之间存在路径，则称该无向图是连通的。

在上述图论的基础上，考虑到编队中成员航天器之间的信息交互以及通信延时，对上述鲁棒控制器增加一协同项，得到协同控制器如式(27)所示：

(27)

式中：τij为电磁航天器i、j之间的通信延时。

2.2 鲁棒协同控制器稳定性证明

本节分析和证明上述控制器(27)的稳定性，选取Lyapunov函数为式(28)，将其对时间求导得到式(29)。将式(22)、式(25)、式(26)代入式(28)，可以得到式(29),双画线部分小于等于零，因此对于Lyapunov函数的证明只需要求证后面部分，即式(30)。

(28)

(29)

(30)

3 电磁航天器编队磁矩优化配置

2.1节建立的航天器编队悬停控制律可以求得航天器在任意位置悬停需要的控制加速度。本节讨论控制加速度的具体实现问题。电磁航天器编队系统有N个成员航天器，编号为i=1,2,3,…,N，成员航天器均能够产生任意指向的磁矩。对于编号为i的航天器，其受到的电磁力表达式为

(31)

式中：Fi为编号为i的航天器受到电磁力的合力；Fij为j号航天器对i号航天器的电磁作用；μi、μj分别为i号航天器和j号航天器的磁矩；rij为i号航天器相对于j号航天器的位置，从j号航天器指向i号航天器。由于电磁力为系统内力，故存在式(32)、式(33)成立：

Fij+Fji=0

(32)

(33)

可以看出整个编队系统受到的电磁力的合力为零，显然在只有相互作用电磁力的情况下，系统质心无法改变，无法实现任意位置的悬停，为此在系统中任选一颗航天器，在该航天器上施加额外推力，通过该推力来改变质心位置。设推力施加在N号航天器上，则满足：

(34)

式中：fo为施加在N号航天器上的悬停外力。

从上述分析中可以看出，电磁航天器编队系统一共受到独立的约束3N个，但是相互独立的变量有3N+3(包含3N个磁矩变量和3个外力变量)个，系统的变量有冗余的自由度，因此可以将该问题转化为带约束的优化问题进行求解。取目标函数表达式为

(35)

4 数值仿真

4.1 仿真参数设置

为验证所设计控制律的控制性能以及磁矩分配方案的可行性，本文对4颗电磁航天器组成的编队进行了仿真计算，航天器编队采用的编队构型如图4所示。

初始时刻4颗航天器位于棱长15 m的正四面体的4个顶点上，参考航天器位于正四面体的中心。假设编队成员航天器的位置和速度在初始时刻受到随机扰动，在运行期间一直存在低于扰动上限的噪声。仿真选择的参考轨道参数，各个状态期望值和初始摄动值分别如表1和表2所示。

成员航天器的质量均为100 kg，线圈半径均为1 m，线圈匝数均为100。控制器的参数选择为Hi=10-2I3×3，εi=10-7I3×3，Λi=10-2I3×3。不确定参数上限的选择参考了文献[21]，分别取ai=10-5，bj=10-7，fi=10-7。考虑3颗航天器链接成环,另外一颗航天器连入该三角形环的通信拓扑结构,权值均取为aij=10-3。成员航天器通信延时为5 s。在磁矩求解时,考虑到能量最优和均衡、电磁力和力矩的解耦以及系统所需外力最小,为使得式(35)每一项的数量及相当，配置磁矩参数取值为W1i=10-11I3×3，W2i=10-9I3×3，γi=102，Wo=105I3×3,然后用MATLAB进行仿真。

图4 电磁航天器悬停编队构型Fig.4 Hovering formation configuration of electromagnetic spacecraft

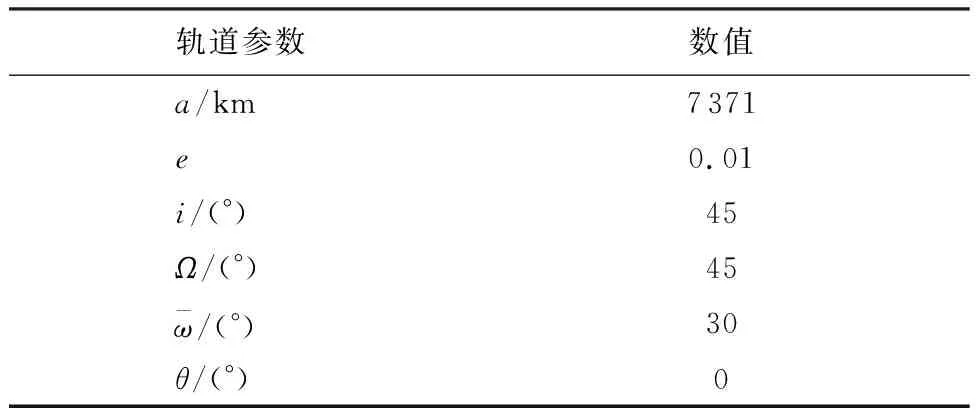
表1 参考轨道参数Table 1 Reference orbital parameters

表2 状态初值信息Table 2 Initial value information of state

4.2 仿真结果

仿真结果如图5～图11所示。图5和图6为相对位置跟踪误差曲线，图7和图8为相对速度跟踪误差曲线。图9～图11分别描述了控制磁矩、电磁力、编队悬停外力的变化规律。

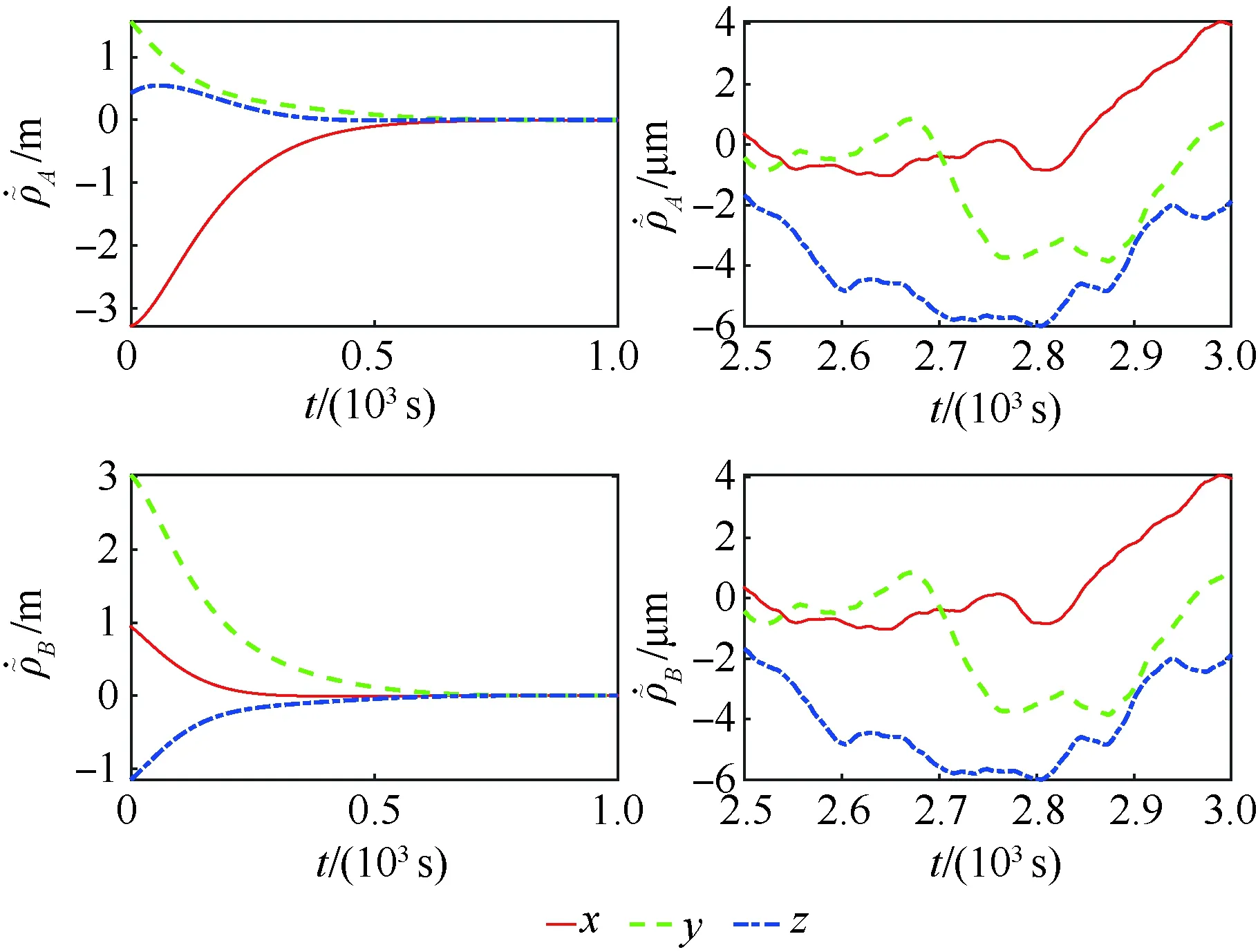
图5 AB相对位置跟踪误差曲线Fig.5 Tracking error curves of AB relative position

图6 CD相对位置跟踪误差曲线Fig.6 Tracking error curves of CD relative position

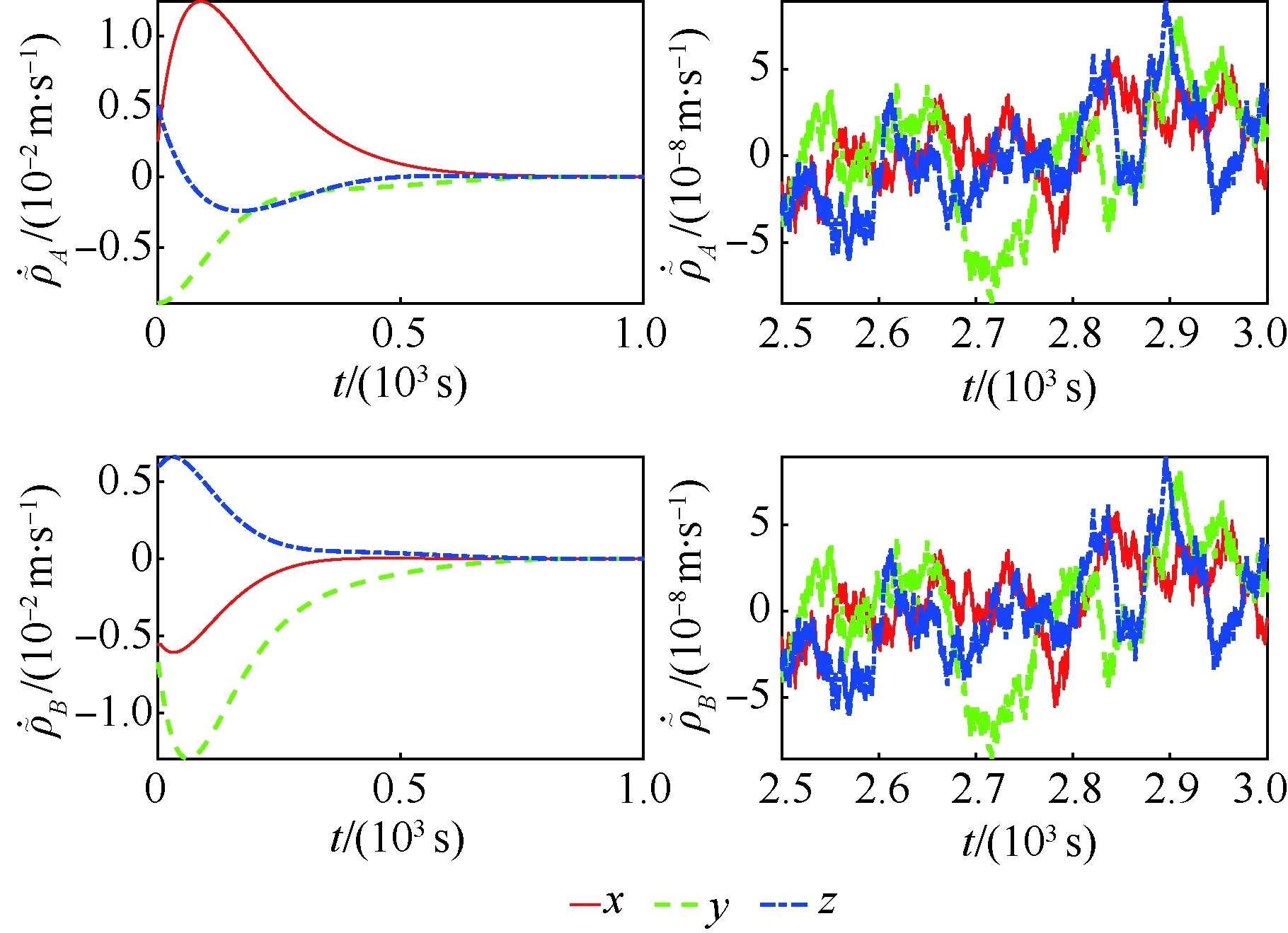
图7 AB相对速度跟踪误差曲线Fig.7 Tracking error curves of AB relative velocity

从图5、图6可以看出，在位置初值、速度初值均存在随机扰动并且状态信息存在噪声的情况下，本文设计的鲁棒协同控制律利用航天器之间的电磁力能够在700 s内回到期望轨道，且位置跟踪误差在10-6数量级。从放大的结果也可以看出，控制器中的协同项最终使得编队中所有航天器的位置跟踪误差趋于一致，这有利于误差的管理。

图8 CD相对速度跟踪误差曲线Fig.8 Tracking error curves of CD relative velocity

图9 控制磁矩曲线Fig.9 Curves of control magnetic moment

图10 电磁力曲线Fig.10 Curves of electromagnetic force

图7和图8表明，协同控制律可以使成员航天器对速度的跟踪误差达到10-8数量级，具有较高的精度，同时也说明设计的控制器具有较强的鲁棒性和协同性。

从图9可以看出,优化之后的控制磁矩数量均小于105，该磁矩可以使用超导线圈实现。图10表明编队悬停控制所需的电磁力在10 mN量级,一方面这样的小推力可以使得控制精度有所提升，另一方面也表明电磁力只能实现近距离的编队。图11为编队悬停时为了改变航天器质心所需要的外力，从图中可以看出其大小和所需的电磁力相当。

图11 编队悬停外力曲线Fig.11 Curve of formation hovering external force

4.3 有无协同控制效果比较

为了分析在控制律中引入协同项的效果，在同样的初值下对未引入协同的情况也进行了仿真。选取文献[22]中的暂态构型维持误差σ作为评价指标，其具体形式为

(36)

式中：σ越小表明暂态构型维持能力越强。从图12中可以看出，在编队成员均存在5 s通信延时的情况下，尽管在200 s附近有无协同指标略低于有协同指标的情况，但是从整体趋势来看，有协同的控制器表现出了更好的性能。

为分析设计的控制律的能量消耗情况，本文采用系统各成员航天器所受力的模之和作为能量评价指标，记为E。在相同初值下对编队开环控制的能量指标进行了计算，结果如图13所示。

图12 暂态构型维持位置误差曲线Fig.12 Curve of transient configuration position keeping error

以上仿真结果表明本文设计的电磁航天器编队鲁棒协同控制律能够有效实现航天器编队任意位置的悬停，对系统存在的内部和外部不确定性具有较强的鲁棒性，文中给出的基于能量最优和均衡的磁矩配置方案能够实现磁矩的有效分配。

图13 能量消耗对比Fig.13 Comparison of energy consumption

5 结 论

本文针对近地近圆轨道附近电磁航天器编队悬停问题，设计了一种有效处理绝对轨道信息缺失的控制方法，具体如下所述。在电磁力模型和动力学模型均存在不确定性的条件下, 通过引入滑模控制理论和一致性理论，设计了鲁棒协同控制律。考虑到能量最优和控制均衡以及轨道姿态的解耦，给出了磁矩的优化配置方案。分析证明了所设计的协同控制律的稳定性及鲁棒性。仿真结果表明，位置跟踪误差和速度跟踪误差分别能达到10-6、10-8数量级，所给出的磁矩分配方案能够实现磁矩的合理分配，控制中引入协同项后可以提高编队的协同能力，且能平衡各成员航天器之间能量消耗。