基于空间两点的视觉自主着陆导引算法设计
魏祥灰, 唐超颖, 王彪
(南京航空航天大学 自动化学院, 南京 211106)
垂直起降无人机(UAV of the type Vertical Take Off and Landing,VTOL UAV)被越来越广泛地运用到动目标跟踪、紧急着降以及危险救援等任务[1-2]中,这对其导引效率与精度要求越来越高[3]。由于GPS信号的局限性,基于视觉传感器的导引方式受到了越来越多的关注[4-5]。本文以无人机着陆为背景,采用视觉传感器,设计和研究垂直起降无人机的高效率导引算法。
目前,从实现导引的方式上,国内外的无人机视觉着陆研究可分为基于位置的导引方式和基于速度的导引方式,这2种方式都需要使用视觉解算当前位置,容易引入计算误差[6]。其中基于位置的导引方式[7-8]是指利用视觉信息解算无人机当前位置,计算其与预设基准轨迹的位置偏差,采用纠偏处理,使无人机按照既定的轨迹飞行。这种导引方式便于理解分析,被当前大多数研究人员采用[9-10]。基于速度的导引方式[11-12]是指建立无人机当前位置与速度指令之间的关系,不计较导引过程中的位置误差,以一定着陆精度完成定点着陆。这种方式具备计算复杂度低、实时性好等特点,能够快速高效地完成导引任务。Min等[13]采用基于速度的导引方式,设计以时间为基础的纵向加速度指令生成算法,实现竖直方向上的着陆。
另外,为实现无人机精准导引,目前使用的导引法主要有比例导引法、速度向量场法和线性反馈法等[14]。比例导引律是指飞行器在攻击或者追踪目标的导引过程中,速度矢量的转动角速度与目标瞄准线(视线)的转动角速度成比例的一种导引律[15],在导引的末端,运动轨迹近似为直线,不能满足垂直起降无人机着陆瞬间速度方向竖直向下的要求,在无人机着陆领域,比例导引法使用很少。速度向量场法是一种常用的无人机导引方法。针对垂直起降无人机,国内外学者几乎都采用“直角型”的转弯方式[16-17]。由此设计的速度向量场,需要无人机在“直角点”悬停一段时间再转弯飞行,这严重影响了无人机着陆效率。假若不悬停、直接直角转弯,对无人机的方向机动性性能要求过高,难以工程实现。张炳亮[18]设计了基于圆的速度向量场,但该方案只适用于飞行高度与水平着陆距离相当的情况,不具有普适性。
针对以上无人机着陆效率较低的问题,一方面,从减少着陆路程和降低飞行机动性能要求的角度,设计速度向量场,提高无人机的转弯效率。另一方面,采用基于速度的着陆导引方式,选取合适的视觉合作特征,建立图像信息与速度指令之间的直接关系。避免位置解算及其引入的计算耗时和误差,提高着陆导引效率。
本文首先结合无人机着陆的速度方向以及转弯能力等要求,设计速度向量场,同时讨论相关参数与无人机性能的约束关系;然后,研究图像特征与航迹倾斜角、航迹方位角和速度大小的关系,推导出合理的着陆导引规律;最后,利用Simulink仿真平台验证本文设计导引律的正确性和准确性。
1 速度向量场的设计与分析
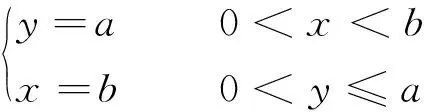
本节以1/4椭圆弧为单位,设计着陆的速度向量场,并分析此时无人机的机动性能要求。以弧上各点的切线方向确定航迹倾斜角的理想值(见图1),从而满足着陆瞬间机体速度方向竖直向下的需求。定义航迹倾斜角γ为机体速度Vb与水平面的夹角。建立纵平面的坐标系,其中C1点为目标位置,椭圆表达式为
(1)
式中:x≥0,y≥0,a>0,b>0,椭圆弧与y轴的交点为(0,a),与x轴交点为C1:(b,0)。设椭圆曲线上任意一点M的坐标为(xM,yM),则该点航迹倾斜角γM为
(2)
以x=0以及x=2b轴上任意点,与C1点作椭圆弧,建立目标着陆点周围的速度向量场(见图2)。空间中任意一点N(xN,yN)的航迹倾斜角γN表达式为
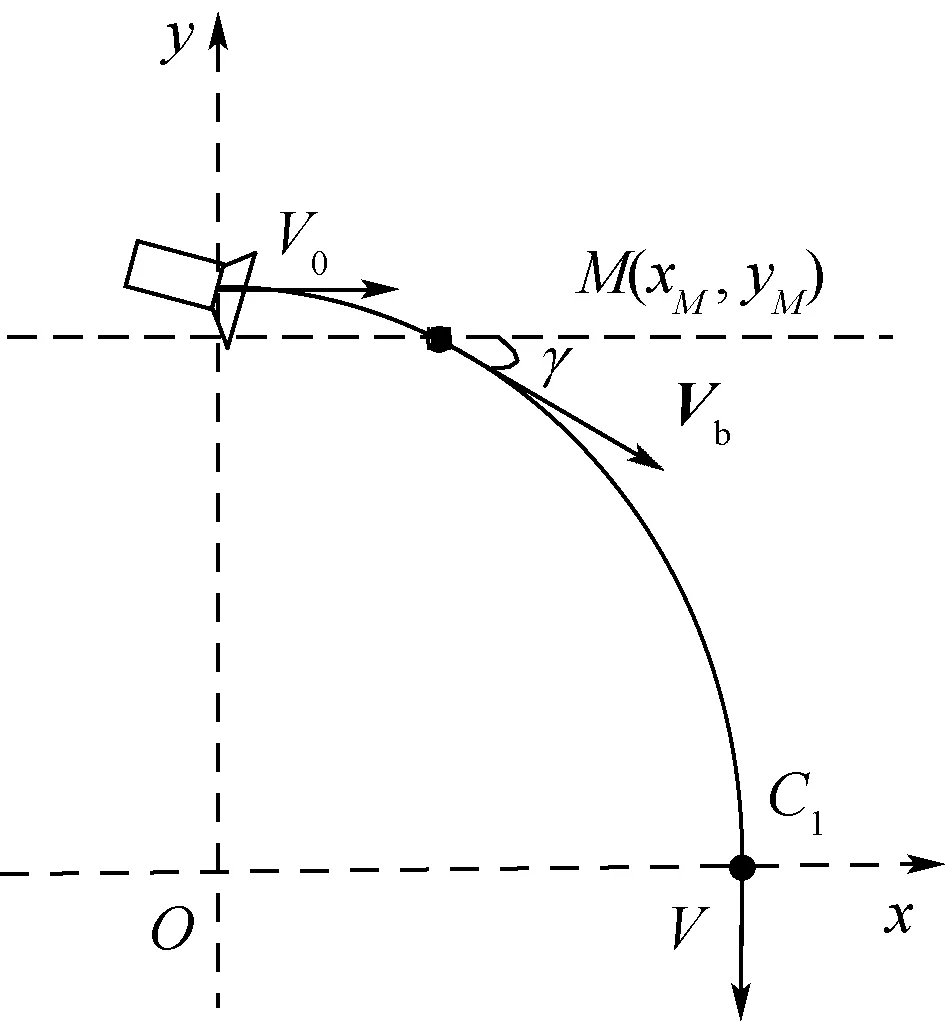
图1 椭圆弧示意图Fig.1 Schematic diagram of elliptic arc
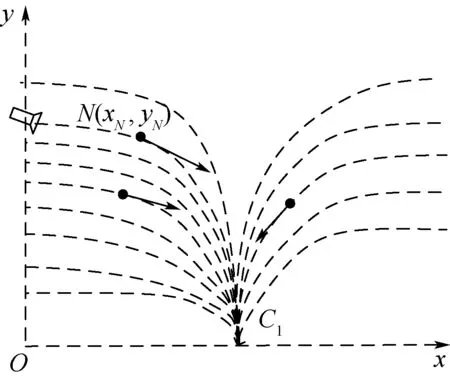
图2 速度向量场示意图Fig.2 Schematic diagram of velocity vector field
(3)
式中:aN为点N所在椭圆弧与y轴交点的纵坐标。
以轨迹中各点的曲率半径为衡量指标,分析椭圆弧对机动性能的要求,半径越小表示对无人机转弯机动能力要求越高。假设着陆的光滑曲线L在着陆平面上的表达式为yL=f(xL),则点(xL,yL)的曲率半径为
(4)
若点(xL,yL)不可求导,则
lim(R(xL,yL))=0
(5)
将式(1)代入式(4)计算轨迹的曲率半径,得到最大曲率半径Rmax与最小曲率半径Rmin分别为
Rmax=(max{a,b})2/min{a,b}
(6)
Rmin=(min{a,b})2/max{a,b}
(7)
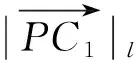
结合式(7),若无人机固有的转弯机动性能对应的转弯半径为Rplane,则满足约束条件Rplane 无人机在三维空间中的速度方向由航迹倾斜角γ和航迹方位角χ两个角度确定,其中航迹方位角表示速度在水平面的投影与地面固定轴的夹角。 机体坐标系XbYbZb、相机坐标系XcYcZc以及像素坐标系uv之间的关系如图4所示,其中特征点C1的像点c1在相机光轴上,这是由云台的跟瞄功能保证的,在无人机的飞行过程中,相机能完成快速对准,使得光轴OcZc一直保持指向点C1。机体坐标系一点P(xb,yb,zb)在图像中的像点坐标为(u,v),由相机成像原理可知两坐标关系为 (8) 式中:Du=-zcdu/f,Dv=-zcdv/f,f为相机焦距,du与dv分别为像素坐标系u轴、v轴方向上单位像素对应的物理长度,一般地,du=dv;zc为点P在相机坐标系下的Z轴坐标;u0与v0为相机主点位置;Rbc与Tbc分别为机体坐标系与相机坐标系之间的旋转矩阵和平移矩阵。 (9) 图3 本文导引律的结构框图Fig.3 Structure diagram of proposed guidance law 图4 机体坐标系与像素坐标系的关系示意图Fig.4 Schematic diagram of relationship between body coordinate system and image coordinate system (10) (11) 则Rbc表达式为 (12) 由式(8)可得图像中某一向量(Δu,Δv)对应机体坐标系下的Xb-Yb二维单位矢量(Δxb,Δyb)的关系如下: (13) 式中:k为尺度因子;R的表达式为 (14) (15) 代入式(13),可得航迹方位角指令χcmd表达式为 (16) 由式(16),得到图像信息与航迹方位角指令的关系,接下来探讨图像信息与航迹倾斜角的关系,用图像信息表示公式(3)。图5展示了无人机与合作特征的空间关系,其中α为相机光轴与世界坐标系-Zw轴的夹角,β为视线MC1与MC2构成的夹角,α与β反映了机体与目标之间的相对位置关系,并且满足α≥β。 其中由ΔMC1C2的正弦定理可得 (17) 点M(xM,yM)坐标表达式为 (18) (19) 将式(17)代入式(18)与式(19),得到α、β与点M坐标的关系为 (20) (21) 将式(20)、式(21)代入式(3),得到点M处航迹倾斜角指令γcmd的表达式为 (22) 式中:b为无人机在初始位置时与目标点的水平距离: (23) 式中:下标0表示相应变量的初始值;α的大小由云台系统给出的2个转角(倾角θY和滚转角φY)求出: (24) 目标视线夹角β与图像信息之间的关系如图6所示,其中Occ1⊥c1c2,得出β的表达式为 (25) 联列式(22)~式(25)可得点M处,航迹倾斜角指令γcmd与图像信息之间的关系表达式为 在实际应用中,角度测量具有精度限制,同时α、β的测量精度取决于特征矢量的高度C。接下来讨论角度精度与特征高度之间的关系。假设无人机从距离着陆点竖直高度为h,水平距离为l的位置着陆,则得到本文设计的椭圆着陆轨迹的参数表达式为 (26) 式中:0<θ<π/2。假设无人机着陆末端允许的竖直高度偏差为hT,即当高度小于等于hT时,无人机可以将速度降为0。则由y=hT得到着陆末端允许的最大位置偏差(Δx,Δy)为 (27) 如图5所示,设无人机某一点的位置为(x,y),特征点C1、C2的空间位置分别为(b,0),(b,-C)。由ΔPC1C2中的余弦定理,可得α、β与(x,y)的关系为 (28) 由式(28)可知,在确定无人机和目标点的位置时,合作矢量的高度C与β成正相关。将式(1)代入式(28)得到β与y之间的关系: β=arccos(g(y)) (29) 经计算g(y)在x≥0、y≥0的范围内为关于y的单调递减函数,故β的大小与y为正相关。假设合作特征高度矢量的高度值为C,利用式(27)计算得到的偏差(Δx,Δy)代入式(29),可得 Δβ= (30) 若(Δx,Δy)表示无人机能够允许的位置偏差,则相应的Δβ表示着陆系统允许的β值的测量偏差(即目标视线夹角的精度,用dβ表示),由此可得精度dβ与C的关系: dβ= (31) 同理可得α的精度dα: (32) 由此可知,在针对不同对象和场景应用时,可以根据应用背景的参数h、l,以及无人机和相机传感器的性能参数hT、dβ求出对应的合作矢量的高度C。 由于α≥β,故本文建立α与速度大小指令|Vcmd|的关系。将式(1)代入式(28),xP为无人机与目标的水平距离,则α与xP之间的关系表示为 α=arctan(f(xP)) (33) 经计算f(xP)在xP≥0,yP≥0的范围内为关于xP的单调递减函数,故α与xP呈负相关。由于|Vcmd|与xP也呈负相关。故本文以参数α1、α2构成速度大小指令|Vcmd|的分段函数如式(34)所示,其中V0为无人机初始速度的大小,当α2>α>α1时,|Vcmd|的变化与α的变化成比例关系。 (34) 综上,无人机的机体坐标系下速度指令: (35) 传统着陆轨迹与本文着陆轨迹如图7所示。其中传统着陆方式下的轨迹表达式为 (36) 对比本文提出的轨迹表达式(式(1)),得到着陆距离L1、L2分别为 (37) 由此可见,在本文提出的着陆距离更短,并且水平方向距离目标越远(b值越大),本文算法在着陆距离上的优势越明显。 另外,分析比较2种轨迹的最小曲率半径,以此评价2种着陆方式对无人机的转弯机动性能的需求。本文设计轨迹的最小曲率半径由式(7)给出,当参数a或b固定,满足a=b时,理想轨迹的最小曲率半径Rmin最大。由式(4)、式(5)的曲率半径计算原理,得到传统轨迹的曲率半径RT为 (38) 由此可见,与传统着陆方式相比,本文的着陆轨迹对机动性能要求更低。传统方式要求转弯机动性能无限高,而这在实际应用中无法达到,所以工程中通过在转弯处悬停的方式,通过消耗时间,降低对机动性能的高要求。 综上,与传统着陆方式相比,本文的导引方法实现了着陆距离更短,机动性要求更低,效率更高。 图7 着陆轨迹的比较Fig.7 Comparison of landing trajectory 基于Simulink搭建了视觉着陆导引系统仿真平台,将整个系统分为X450四旋翼模型、飞行控制器、着陆导引算法、云台系统、视觉探测算法、小孔成像、目标七大模块,各个模块之间通过各自的输入输出信号建立关联,系统仿真结构框图如图8所示。 图8中,X450四旋翼模型为笔者课题组已有的X450型四旋翼非线性模型,飞行控制器包括机体的速度、姿态、角速率的闭环控制,云台系统由云台模型与云台跟瞄控制器组成,小孔成像模块将世界坐标系中的目标投影到像素坐标系中,视觉探测算法获取目标信息后,将视觉解算信息提供给云台系统。为便于描述,本文假设相机、云台质心与机体质心重合。 (39) 图9(a)为着陆过程中某时刻的状态,其中曲线表示已飞经过的轨迹,左端为无人机的初始位置,右端为当前位置,其中的蓝色图形表示相机的空间姿态,下面的蓝色图形为合作目标,该图可动态地演示视觉导引无人机着陆的全过程。图9(b)为对应的着陆竖直平面内的二维着陆轨迹,其中平行于时间轴的红线表示着陆目标点的高度1 m。 无人机的导引指令在着陆过程中的变化如图10所示,航迹倾斜角指令γcmd由初始值逐渐增加到末端期望值(图10(a));航迹方位角指令χcmd与期望值曲线走势一致,并在期望值上下波动,这主要受成像误差的影响(图10(b));随着无人机越来越接近目标,速度越来越小(图10(c)),到达目标位置时,速度方向指令接近竖直向下,大小为零。 图8 系统仿真平台结构框图Fig.8 Structure diagram of system simulation platform 图9 无人机着陆过程仿真示意图Fig.9 Schematic diagram of UAV landing process simulation 图10 导引指令随时间的变化Fig.10 Variation of guidance command with time 无人机速度响应、位置响应以及航迹倾斜角响应值在着陆过程中的变化如图11所示,可见,在本文算法约束下,无人机在接近目标点时,速度缓慢降低,到达目标位置时,速度大小为零,方向竖直向下,实现了垂直软着陆。 航迹倾斜角指令是由图像信息解算的目标视线夹角β以及云台偏角α计算所得,接下来验证角度的测量准确性。图12和图13分别表示着陆过程中,两夹角的真实值与测量值的关系。其中真实值与测量值的绝对误差值Δβ与Δα的表达式为 Δβ=|β-βr| (40) Δα=|α-αr| (41) 由式(40)得到误差Δβ一直保持在0.14°内,α的测量值在着陆始端误差不超过0.9°,并且随着无人机距离目标越近,很快误差保持在0.1°以内。由此可知本文算法能准确地解算出角度值,并且距离目标越近则准确度越高,满足实际应用的要求。 图11 响应随时间的变化Fig.11 Variation of response with time 图12 β角分析Fig.12 β angle analysis 图13 α角分析Fig.13 α angle analysis 在无人机着陆中的导引研究中,基本上使用基于位置的方式,为提高导引效率,本文设计了基于空间两点的视觉自主着陆导引算法,为今后实现自主、智能的无人机提供理论研究基础。本文的创新性主要概括为以下2个方面: 1) 突破传统直角型的转弯方式,设计曲线型速度向量场,导引垂直起降无人机曲线着陆,保证末端约束的前提下,提高无人机的着陆效率。 2) 避免传统导引算法中的位置解算,直接建立图像信息与速度指令之间的关系,避免了位置解算引入的计算量和误差,提高计算效率。2 导引律的设计
2.1 图像特征与速度方向的关系
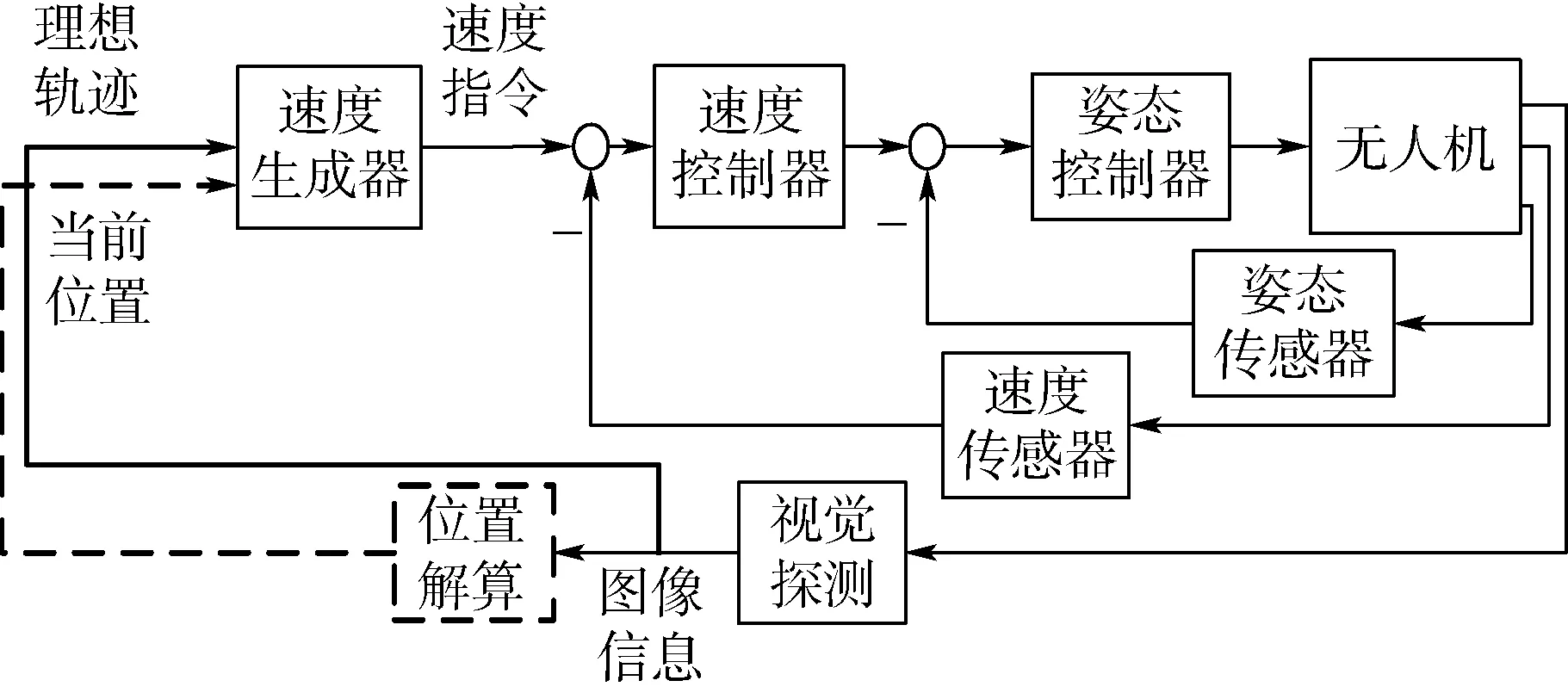
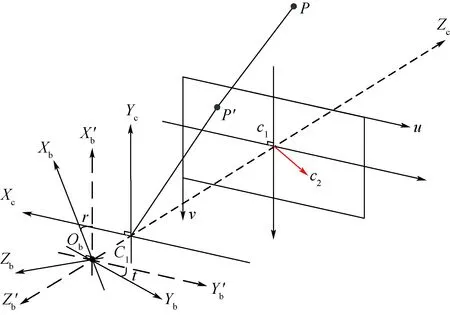
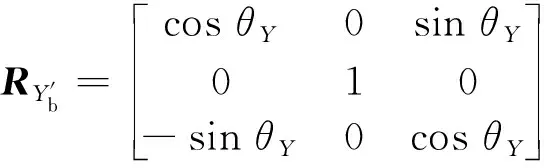
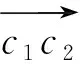
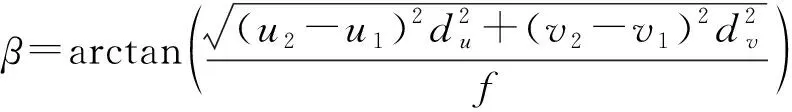
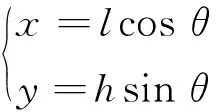
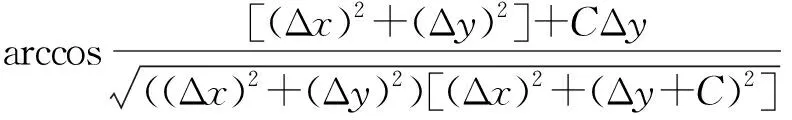
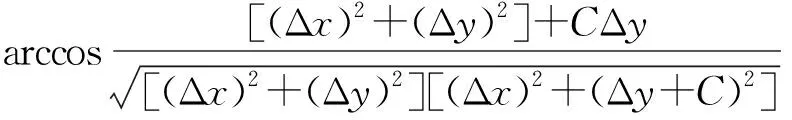
2.2 图像特征与速度大小的关系
3 仿真验证与分析
3.1 与传统方法比较分析
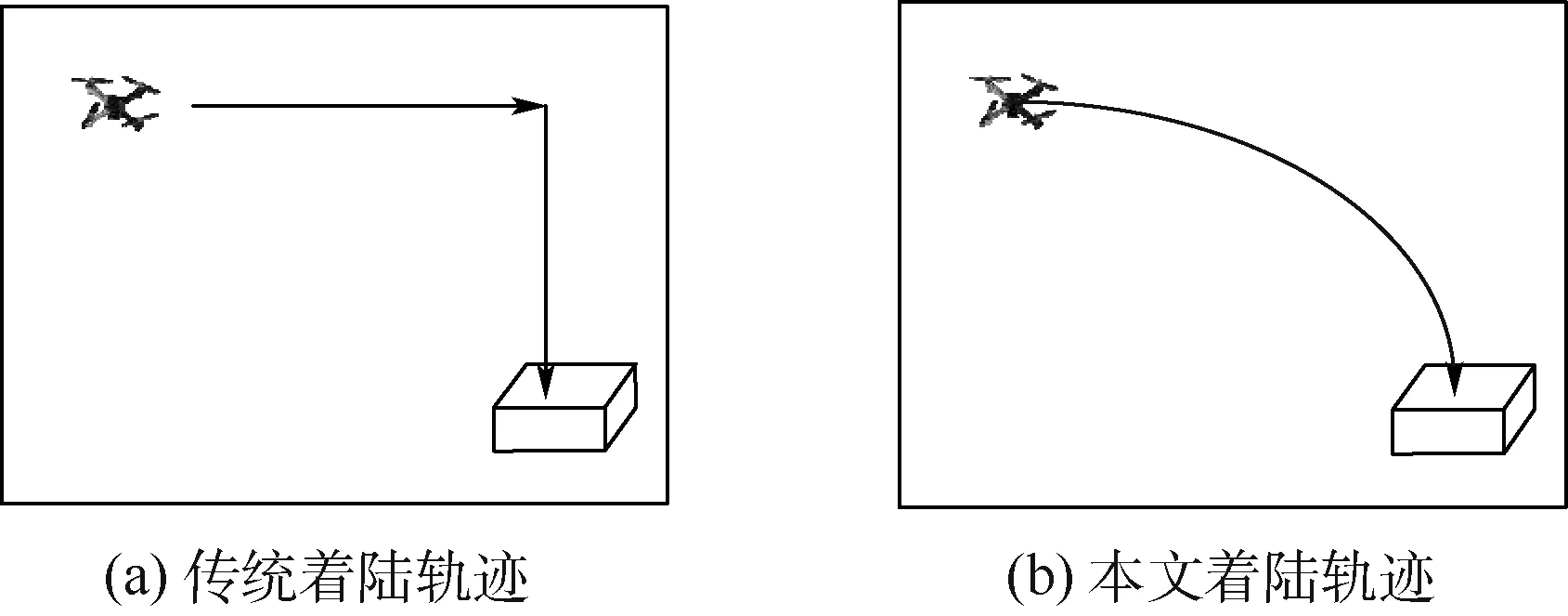
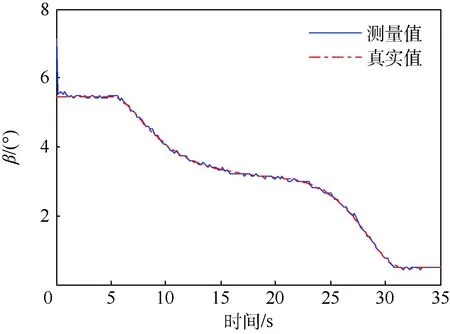
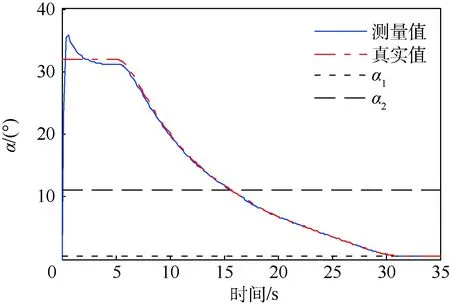
3.2 系统仿真验证
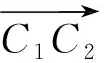
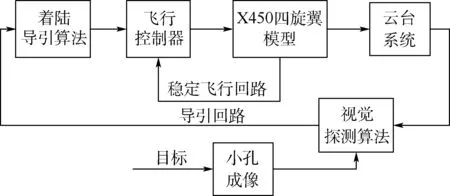
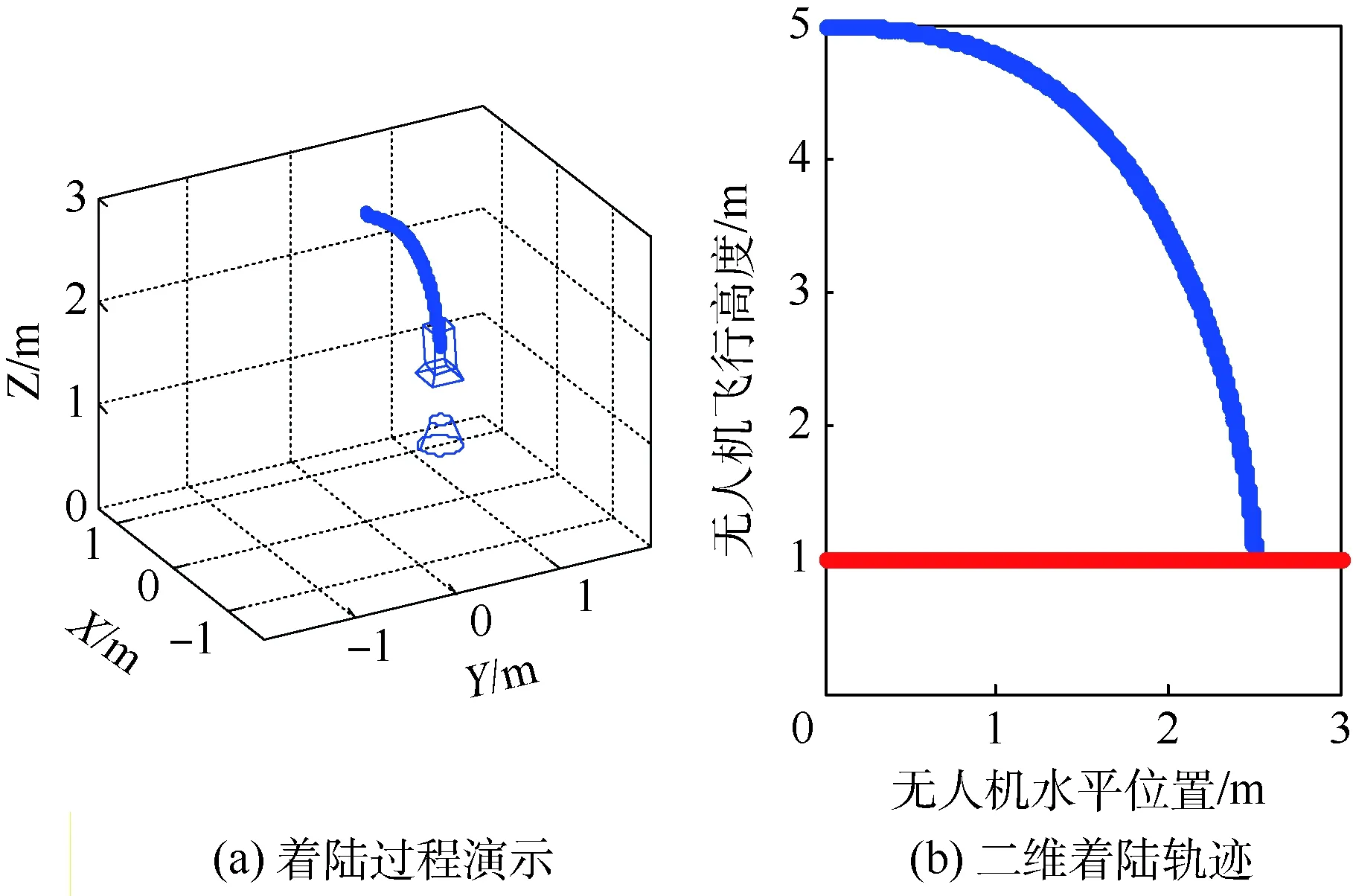
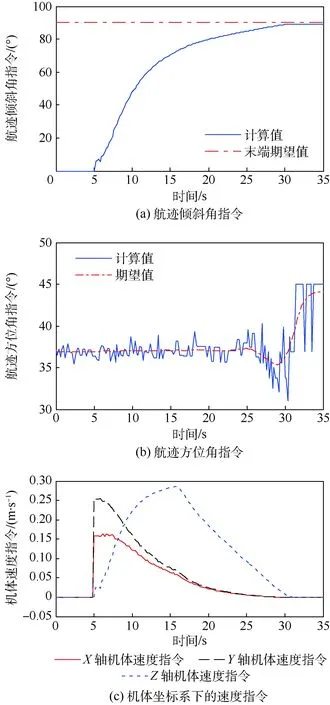
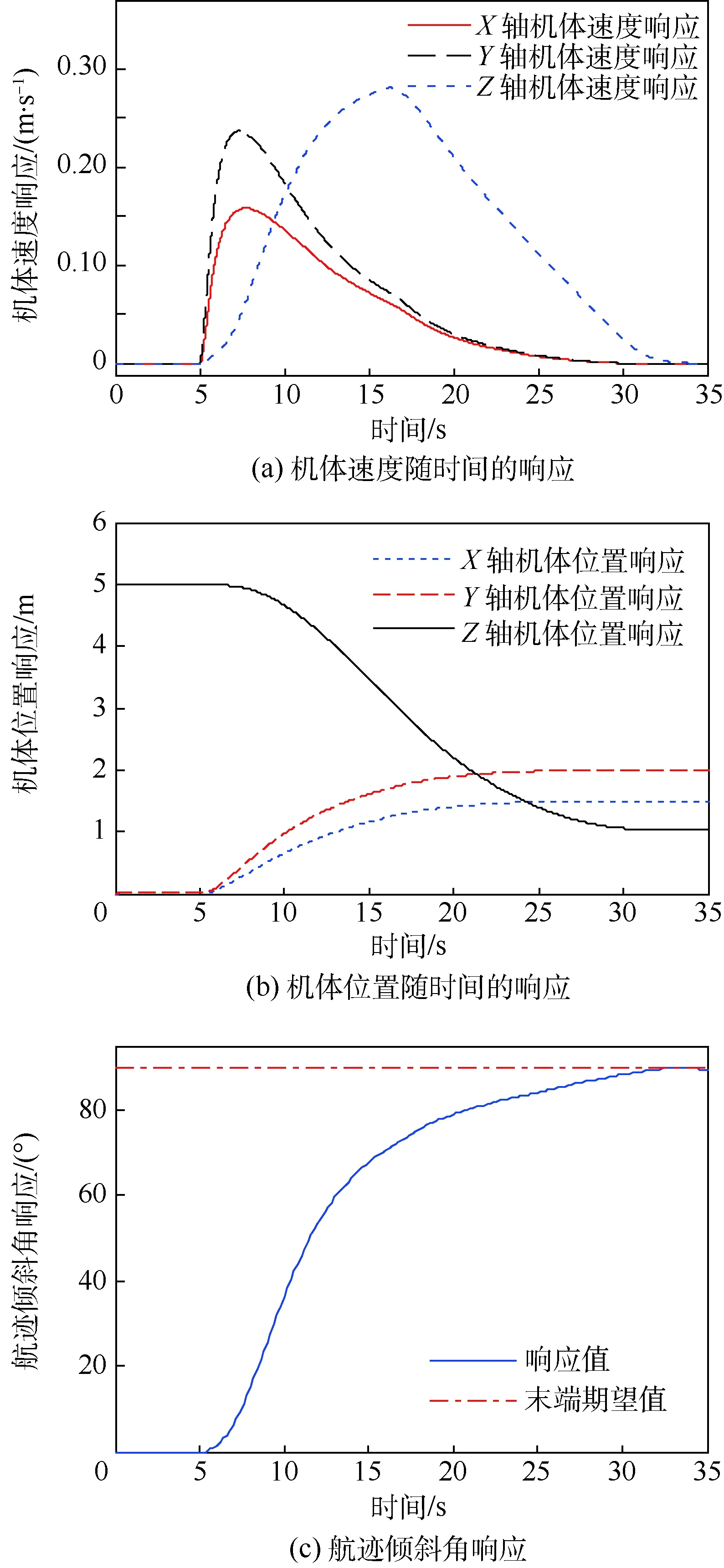
4 结 论


