基于地形匹配的直升机低空飞行前视告警方法

张硕俨， 陆洋

(南京航空航天大学 直升机旋翼动力学国家级重点实验室， 南京 210016)

直升机在飞行过程中，由于缺乏对周围地形感知而发生坠毁的情况，称为可控飞行撞地。利用直升机前视告警系统可有效避免此类事故的发生[1-2]。然而，现有的直升机前视告警系统通常只适用于飞行高度较高的巡航飞行。对于经常需要执行低空飞行任务的直升机，如医疗救护直升机、武装直升机等，当其离地高度很低(通常小于100 m)时，由于告警系统的告警边界过大，会产生持续虚警。因此，为减少直升机低空飞行时告警系统的虚警，需在确保飞行安全的前提下缩小前视告警边界。然而，由于导航误差与地形数据库误差的存在，使得直升机与地形的相对位置也存在一定误差。若仅缩小直升机前视告警边界而不做任何修正处理，将会导致告警失败。可见，如何准确获取直升机与地形间的相对位置是直升机低空飞行前视告警的关键。

国内外对于准确获取运动物体与地形间相对位置这一问题，主要集中在导弹、固定翼飞机、潜艇等领域。文献[3]采用地形轮廓匹配算法准确获取导弹与地形的相对位置，但该算法不允许飞行器进行机动飞行；文献[4]采用桑迪亚惯性地形辅助导航算法修正战斗机与地形的相对位置误差，但该算法在地形梯度变化剧烈区域易造成滤波发散。对于直升机而言，经常需要在复杂的地形上空进行机动低空飞行，因此上述2种方法都不适用于直升机低空飞行告警。而文献[5]采用的互功率谱算法，可准确获取潜艇与地形的相对位置，该算法作为一种性能优良的图像匹配算法，不仅对地形适应性强，而且在匹配时允许潜艇作机动航行[6]。

由于直升机对地形匹配的技术需求与潜艇具有较大的相似性，因此，本文基于互功率谱算法，开展基于地形匹配的直升机低空飞行前视告警方法研究。首先，建立直升机逃逸轨迹模型并确定直升机前视告警边界；然后，基于互功率谱算法进行地形匹配，以准确获取直升机与地形的相对位置，并利用地形熵选择匹配区域提高匹配精度；最后，构建测试算例对本文提出的方法进行仿真验证。

1 直升机低空飞行前视告警方法

直升机前视告警方法的核心是告警边界，目前告警边界的设计方法主要有美国Honeywell公司的告警边界设计方法[7]和基于逃逸轨迹的告警边界设计方法[8]。其中，Honeywell的告警边界为考虑通用性，其边界设计趋于保守，低空飞行时虚警率较高，不适用于直升机低空飞行。基于逃逸轨迹的告警边界设计方法则基于直升机的飞行性能，能够在保证安全的基础上最大程度的缩小告警边界以减小虚警率，因此本文采用该方法。

基于逃逸轨迹的告警边界设计方法，首先需要确定直升机的逃逸轨迹，然后在此基础上设计告警边界。

1.1 直升机逃逸轨迹

直升机的逃逸过程通常可分为3个阶段：飞行员反应、拉起改出和稳定爬升。其中，飞行员反应阶段保持直升机当前状态飞行，稳定爬升阶段以拉起改出阶段最终时刻的状态为基准进行匀速飞行，这两部分均为直线运动轨迹；而拉起改出为机动飞行状态，其轨迹为复杂的空间曲线，是逃逸轨迹中最为关键的部分，直接决定了逃逸轨迹的整体形态。图1示出了直升机逃逸轨迹的3个主要组成部分。

由文献[9]可知，直升机逃逸轨迹的拉起改出部分与抛物线方程拟合度较高，该部分逃逸轨迹高度H可表示为

H=c0+c1x+c2x2

(1)

式中：x为轨迹的横向坐标；c0、c1和c2为待定拟合系数。拟合系数的大小与直升机的飞行性能相关，通常需要基于飞行试验数据拟合求解，亦可利用高精度直升机飞行动力学模型获得，本文采用第2种方法。

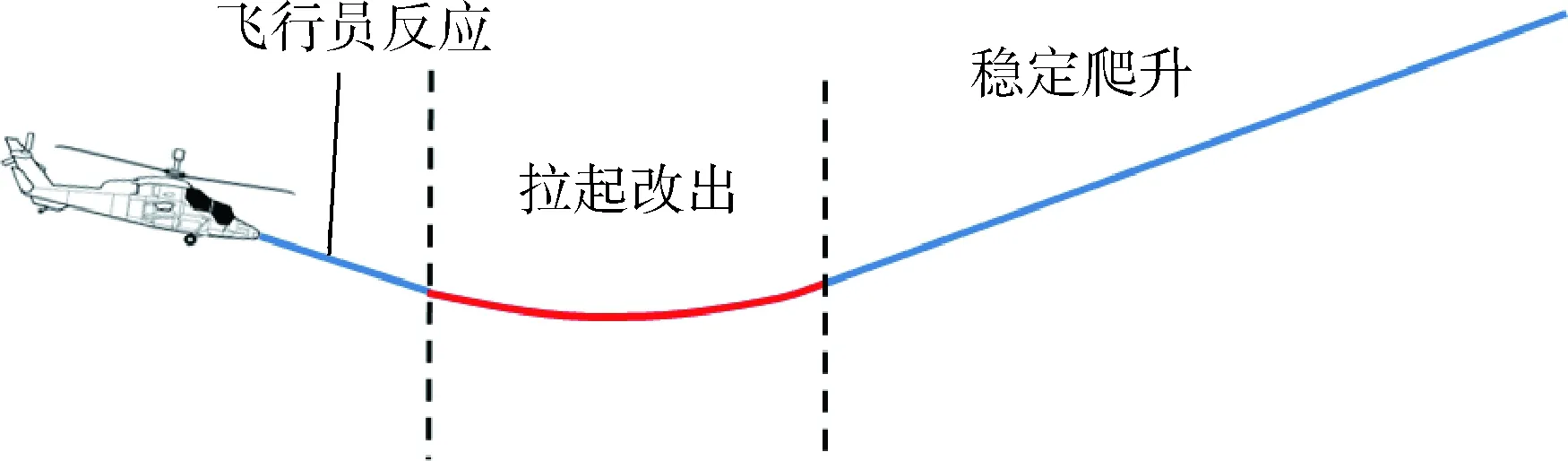
图1 直升机逃逸轨迹各部分组成示意图Fig.1 Schematic diagram of each part of helicopter escape trajectory

在实际应用时，对于给定机型，首先离线计算各种不同组合飞行状态下逃逸轨迹拉起改出部分的拟合系数，在实际飞行过程中，通过多维插值即可获得该飞行状态下的系数值，从而得到相应逃逸轨迹的拉起改出部分。

1.2 直升机前视告警边界

参考文献[10]，将逃逸轨迹中飞行员反应阶段的时间设定为2 s。此外，由于传感器误差以及地形数据库误差等因素的存在，直升机在飞行过程中应在其下方留有一段安全距离，即最小安全高度。在现有直升机近地告警产品中，如美国Honeywell公司的MXKKII，将最小安全高度的最大值设为500 feet(对应高度152.4 m)，对于直升机低空飞行而言，显然不能直接采用。因此，本文根据传感器误差、地形数据库误差以及地形平均斜率等因素，将最小安全高度设为50 m。以UH-60直升机为例，设飞行初始状态为：前飞速度为40 m/s，下降率为4 m/s，则得到告警边界如图2所示。图中：x、z为轨迹坐标。

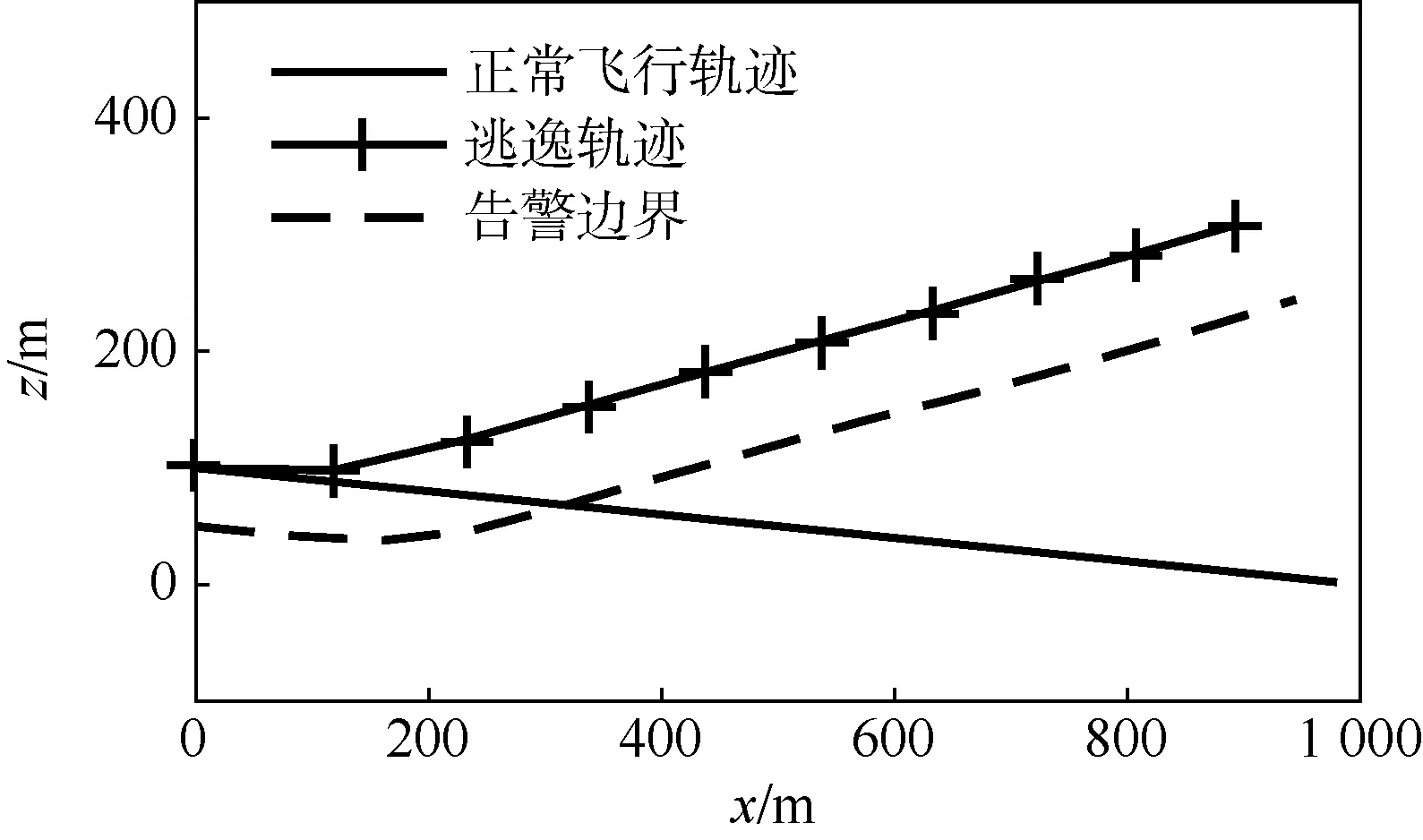
图2 UH-60直升机逃逸轨迹及告警边界示意图Fig.2 Schematic diagram of escape trajectory ands alert envelope for UH-60 helicopter

2 直升机/地形相对位置的准确获取

在确定了直升机前视告警边界后，须进一步准确获取直升机与地形的相对位置，才能进行有效告警。此外，为避免匹配区域选择不当导致的匹配失败，在进行地形匹配之前，利用地形熵选择匹配区域，以提高匹配的准确性。

2.1 直升机低空飞行地形匹配方法

互功率谱算法的基本原理是利用快速傅里叶变换将2个相关矩阵由空域变换到频域，再根据傅里叶变换的位移性质，得到一个反映两者相对误差的脉冲函数[11-12]。将该方法应用于直升机与地形匹配时，须将直升机雷达探测得到的地形高程矩阵和机载地形数据库的地形高程矩阵进行快速傅里叶变换，得到一个互功率谱，由归一化的互功率谱计算出一个脉冲函数，由该函数即可得到直升机与地形的相对位置误差。

直升机雷达探测的地形高程矩阵和机载地形数据库地形高程矩阵的互功率谱G(u,v)可表示为

(2)

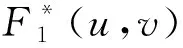
F-1(e-j2π(uΔx+vΔy))=δ(x-Δx,y-Δy)

(3)

当直升机与地形的相对位置误差为0时，该脉冲函数会产生一个明显的冲激峰，其值为1，而其他区域则为0，如图3(a)所示。当相对位置误差较小时，2个地形高程矩阵存在的水平偏移量引起的脉冲函数将产生一个明显的冲激峰。相对位置误差越小，2个地形高程矩阵重叠区域越大，则冲激峰值越接近1，其他区域的值越接近于0，如图3(b)所示。此时冲激峰的位置坐标即为直升机与地形的相对位置误差值。而当相对位置误差很大时，该函数的能量将从单一峰值分散到许多小峰值，如图3(c)所示。图中：X、Y为脉冲函数坐标。

2.2 不同地形对匹配方法的影响分析

此处通过仿真测试，考察不同地形起伏程度对互功率谱算法的有效性影响。首先利用马尔可夫算法随机生成一个起伏程度较大的地形[13]，大小为220×220矩阵网格，地形高程均值为487 m，极差为55 m，方差为81 m2，如图4所示。

在该地形中取出2 个200×200的矩阵作为待匹配地形，两矩阵X、Y方向的平移偏差值均为20。对2个待匹配地形矩阵进行快速傅里叶变换，再计算得到脉冲函数，如图5所示。该脉冲函数中存在一个明显的冲激峰，其坐标为(20，20)，峰值为0.44，由此可得到2个待匹配地形矩阵X、Y方向的平移偏差值均为20。

进一步生成一个起伏程度较小的随机地形，地形高程均值为497 m，极差为5 m，方差为1.6 m2，如图6所示。

同样在该地形中取出2个200×200的矩阵作为待匹配地形，两矩阵X、Y方向的平移偏差值均为20。计算得到脉冲函数如图7所示。可见，该脉冲函数中不存在明显的冲激峰，此时匹配失败。

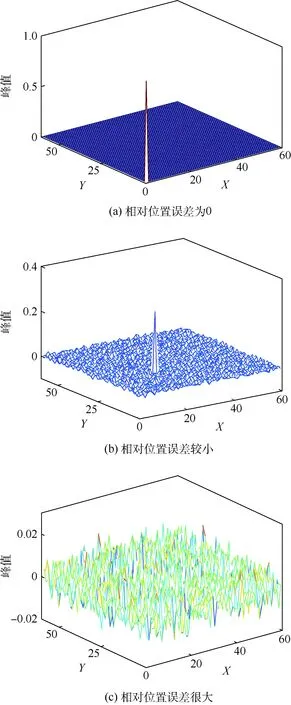
图3 不同相对位置误差下的脉冲函数Fig.3 Pulse functions with different relative position errors

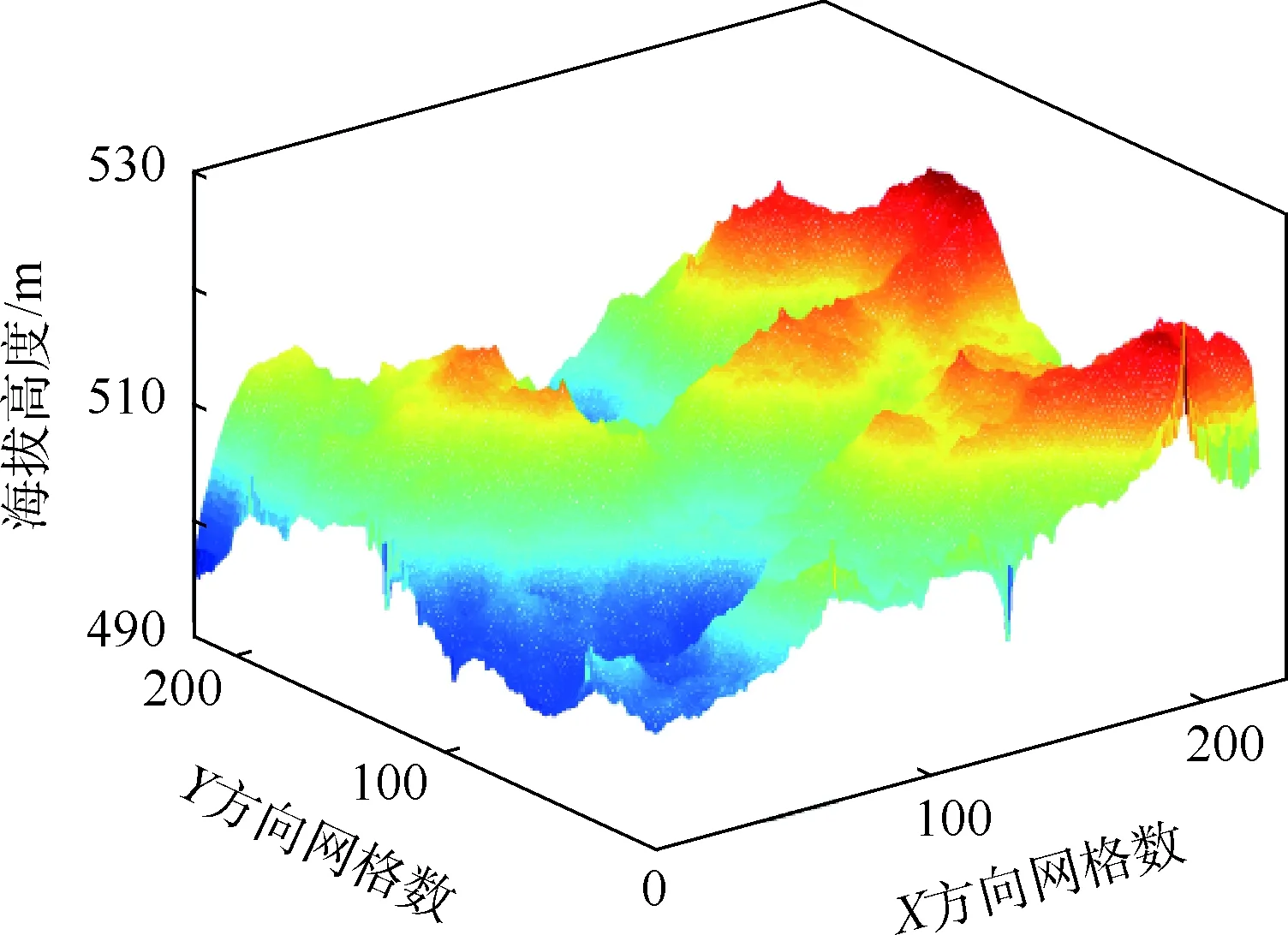
图4 起伏较大的随机地形Fig.4 Undulating random terrain

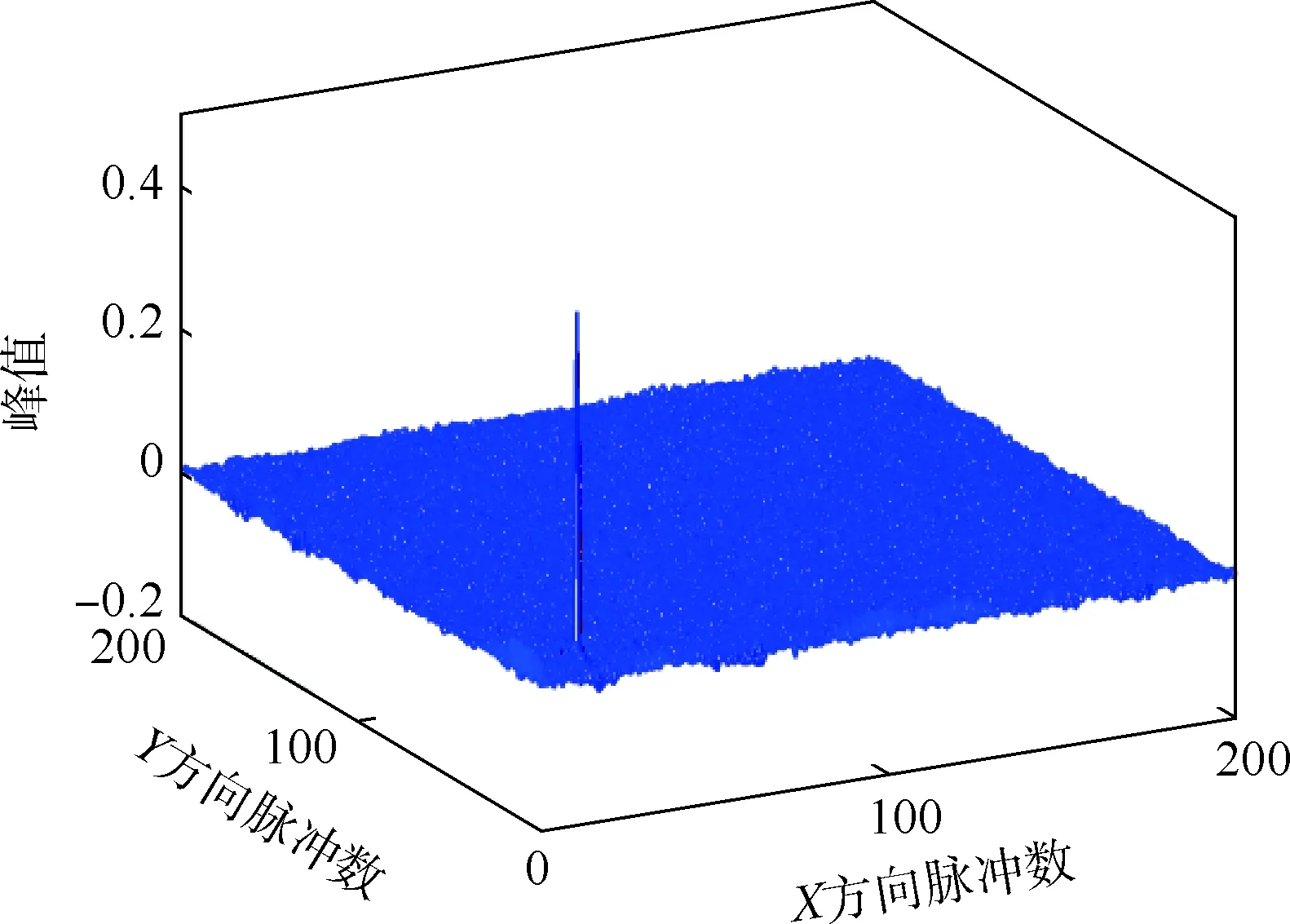
图5 匹配成功时的脉冲函数Fig.5 Pulse function on successful matching

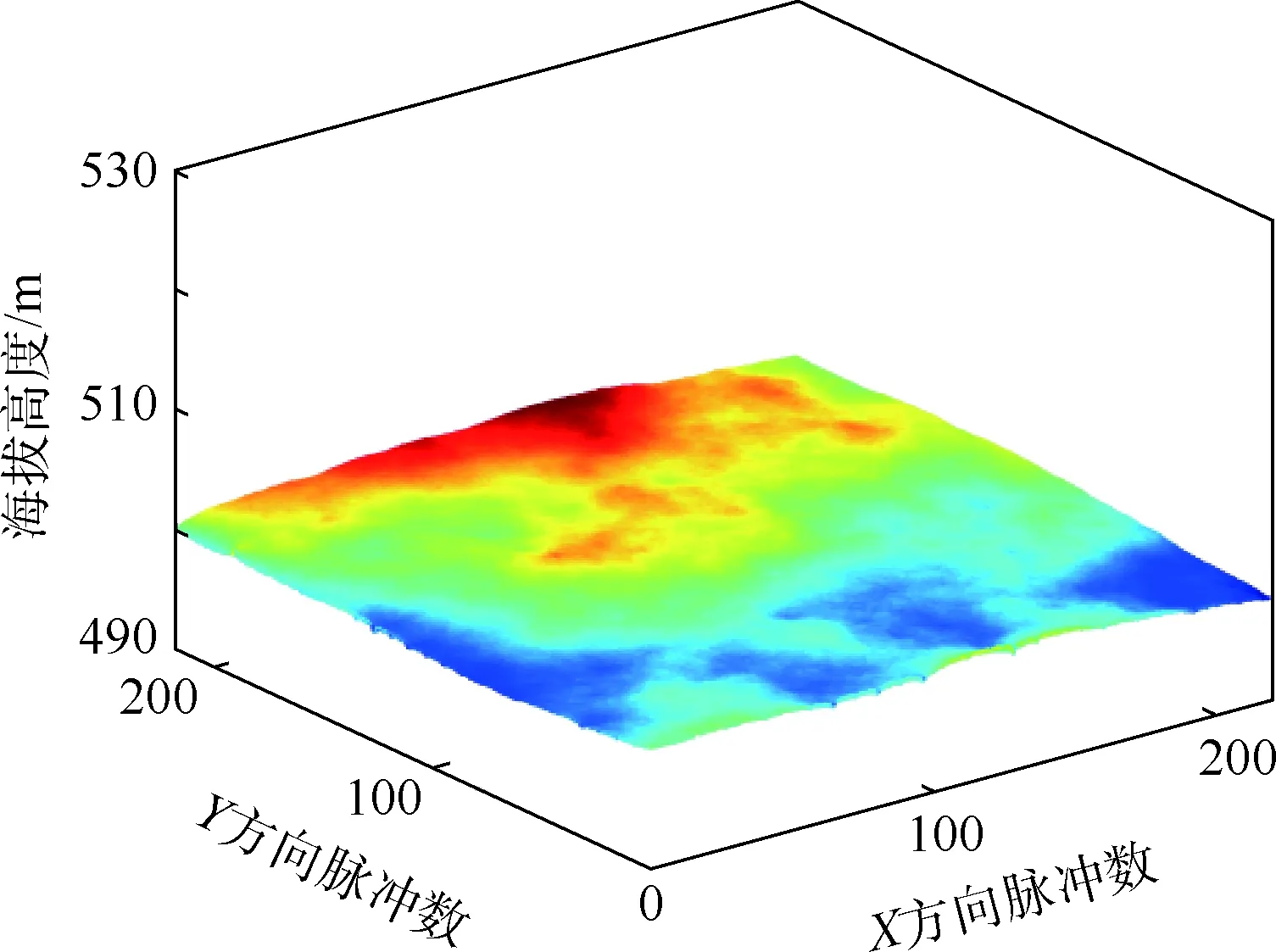
图6 起伏较小的随机地形Fig.6 Small undulating random terrain

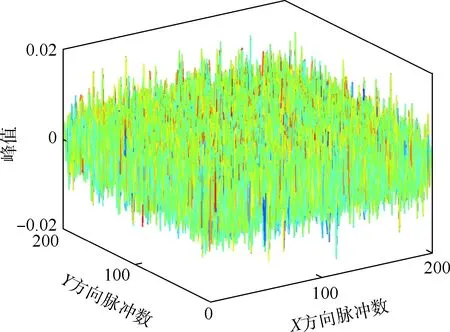
图7 匹配失败时的脉冲函数Fig.7 Pulse function on failed matching

上述仿真测试表明，互功率谱算法的匹配效果受地形起伏程度影响很大，地形起伏程度越大，地形越独特，匹配准确度越高，因此山地等地形较适合地形匹配，而平原、沙漠等地形易导致匹配失败。

2.3 地形熵选择匹配区域

针对平原、沙漠等包含信息量较少的区域，本文参考文献[14]，采用地形熵选择匹配区域方法来解决此问题。

地形熵能够用来描述地形起伏的剧烈程度，当某区域的局部地形高度值变化较为剧烈时，地形所包含的信息量比较丰富，此时计算得到的地形熵较小，而越小的地形熵越有利于进行匹配运算。地形熵的定义式为

(4)

式中：p为无量纲的地形高度值；h为地形高度值；i为地形采样点的序号;M为地形采样点个数的总量；Hterrain为地形熵。

在进行地形匹配前，首先计算直升机当前位置附近区域的地形熵，若地形熵小于预先设定阈值，则进行地形匹配。这样，避免了在平原等区域进行匹配导致的匹配失败，有效提高了地形匹配的准确性。

以图4地形为例，可取出共441个200×200的高程矩阵，参考文献[15]将地形熵阈值设为9，计算得到有25个高程矩阵的地形熵大于阈值，而其中有19个匹配失败。将该25个高程矩阵筛除后，剩余416个矩阵均能够匹配成功。

3 算法仿真测试

本文利用MATLAB开展对基于地形匹配的直升机低空飞行前视告警方法的仿真测试。首先给出算法性能的评价指标，然后给出仿真测试的参数设置，最后给出仿真结果及分析。

3.1 算法性能评价指标

根据文献[16]，此处采用虚警率和告警成功率作为评价告警方法的性能指标。

虚警是指告警系统在直升机安全飞行时给出了不必要的告警，虚警率定义为

(5)

式中：Nu为虚警算例个数；N为算例总数。

告警成功率则是相对告警失败而言的。告警失败是指告警提示过晚，飞行员得到告警信号时已经无法及时改出而导致撞地事故。告警成功率定义为

(6)

式中：Nf告警失败算例个数。

表1给出了前视告警方法的性能指标判断标准。

需要说明的是，计算虚警率和告警成功率的算例总数仅包括产生告警的算例。

表1 前视告警方法性能指标判断标准Table 1 Judgement criteria for performance index of forward looking alert method

3.2 仿真参数设置

为对比验证本文提出的基于地形匹配的直升机低空飞行前视告警方法的优势，仿真中设置了2个测试组，一个为采用本文方法的匹配组，另一个为采用常规告警方法的对照组，2个测试组的告警边界相同，均采用基于逃逸轨迹的告警边界，最小安全高度设为50 m，但对照组未结合地形匹配算法，无法修正直升机与地形的相对位置误差。

1) 地形参数设置：类似图4，仿真地形采用马尔可夫算法随机生成的500组地形，地形高程均值约为400 m，地形矩阵大小均为220×220，设每个矩阵网格大小为90 m，总大小即为19 800 m×19 800 m，2个测试组均在500组地形进行仿真飞行测试。

2) 直升机飞行参数设置：仿真基于UH-60直升机飞行动力学模型。直升机由地形矩阵坐标(20，100)处出发，在500 m海拔高度以40 m/s的速度平飞，无线电高度均值约为100 m，终点为矩阵坐标(160，100)处，每0.5 s主动探测直升机周围10×10矩阵网格的地形数据，并计算地形熵，当地形熵小于9时，则进行地形匹配。飞行期间发生告警或到达终点则停止该次仿真测试。

3) 误差参数设置：测试开始时，2个测试组直升机与地形的位置误差均为3个矩阵网格，即270 m，匹配组与对照组中各有一半测试组的误差方向沿直升机飞行方向，即直升机导航位置位于实际位置前方，另一半误差方向相反，即直升机导航位置位于实际位置后方。

3.3 仿真结果与分析

由3.2节可知，在仿真测试中，对照组存在导航位置误差，告警边界以导航位置为准，而正常飞行轨迹和逃逸轨迹则以实际位置为准。取仿真测试中的典型算例为例，如图8和图9所示。图8(a)、图8(b)为测试中同一地形下的2个测试组，其中匹配组告警成功，而对照组产生虚警。图8(a)中，告警边界、正常飞行轨迹与地形相交，而逃逸轨迹与地形不相交，此时告警成功。图8(b)中导航位置在实际位置前方，告警边界与地形相交，而正常飞行轨迹、逃逸轨迹与地形不相交，此时为虚警。图8(c)为该地形下，2个测试组直升机与地形相对位置误差随时间变化的曲线。从图中可以看出，仿真开始时2组的相对位置误差均为3个矩阵网格，但匹配组通过地形匹配修正了这一误差。

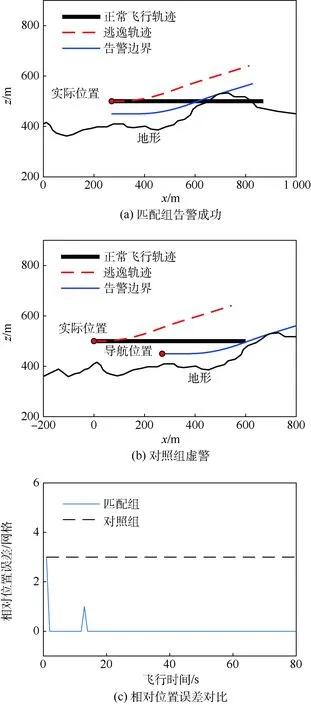
图8 对照测试AFig.8 Controlled trial A

图9(a)、图9(b)为仿真测试中同一地形下的另外2个测试组，其中匹配组告警成功而对照组告警失败。图9(a)所述状态与图8(a)相似，为告警成功。而图9(b)中导航位置在实际位置后方，告警边界、正常飞行轨迹、逃逸轨迹均与地形相交，此时告警失败。图9(c)为该地形下，2个测试组直升机与地形相对位置误差随时间变化的曲线。同样可以从图中看出，匹配组通过地形匹配修正了相对位置误差。

完成对照组、匹配组各500组仿真测试算例后，得到的测试结果如表2所示。

从表2的仿真结果可以看出，对于采用地形匹配的本文告警方法，相比于常规告警方法，虚警率明显降低(约16%)，告警成功率显著提高(近30%)。

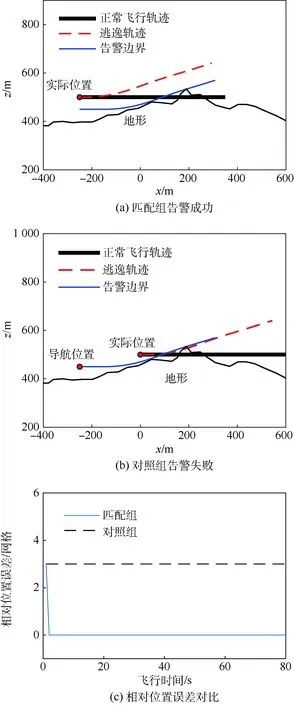
图9 对照测试BFig.9 Controlled trial B

表2 告警方法仿真测试结果Table 2 Simulation test results of alert method

4 结 论

本文将基于互功率谱算法的图像匹配方法应用于直升机地形匹配，有效地修正了直升机与地形的相对位置误差，并据此提出了直升机低空飞行前视告警方法，有效实现了直升机低空飞行防撞告警。主要结论如下：

1) 互功率谱算法的匹配效果受地形起伏程度影响，地形起伏程度越大，地形越独特，匹配准确度越高。

2) 对于直升机低空飞行状态，未结合地形匹配的常规告警方法由于直升机与地形的相对位置不准确，导致告警成功率低、虚警率高。结合地形匹配后的前视告警方法告警成功率显著提高，虚警率明显降低，证明了本文提出的前视告警方法能够很好地适应直升机低空飞行的防撞告警要求。