具有初始热变形的转子系统振动响应分析
马艳红, 刘海舟, 邓旺群, 杨海, 洪杰,*
(1. 北京航空航天大学 能源与动力工程学院, 北京 100083; 2. 先进航空发动机协同创新中心, 北京 100083;3. 中国航发湖南航空动力机械研究所, 株洲 412002; 4. 航空发动机振动技术航空科技重点实验室, 株洲 412002)
随着航空发动机向高负荷、轻质化的方向发展,转子系统的振动问题越来越突出。当这类发动机停车后再次起动(即热起动)时,发动机内的温度分布不均会使转子系统产生初始热变形,进而使转子振动响应进一步恶化,甚至导致发动机起动失败。事实上,国内外对发动机在热起动过程中由初始热变形引起的振动过大的故障屡有报道。朱梓根和晏砺堂[1]对某涡桨发动机在热起动过程中出现较大的振动响应,甚至引起转静子碰摩故障的现象进行了研究。张连祥等[2-3]对某涡扇发动机在热起动过程中振动过大的原因进行了分析。Marinescu[4]与Baldassarre[5]等发现,当发动机热起动时,轴承上会出现较大的动载荷。因此,准确描述和分析初始热变形对转子动力学特性的影响具有重要的工程意义。
在早期研究中,关于初始热变形对转子振动响应影响的研究多以转轴初始热弯曲为重点,并以简单转子模型为对象开展理论分析。Nicholas等[6-7]通过Jeffcott转子模型,从幅值和相位的角度详细分析了转轴初始弯曲对其不平衡响应的影响规律,并提出了相应的平衡方法。Shiau和Lee[8]在Nicholas等[6-7]的基础上进一步完善,考虑了转轴初始弯曲对转子在初始不平衡和轮盘初始倾斜下响应的影响。近年来,研究对象逐渐转变为实际的、较为复杂的转子系统,但对初始热变形影响的研究仍以转轴初始热弯曲为主。Pennacchi等[9-10]通过对转子施加与转速同步旋转的弯曲力矩,研究了带有初始热弯曲的转子的故障诊断方法,并以实际发动机故障为例,验证了诊断方法的可行性。Sanches和Pederiva[11]也进行了相似的研究,他们对同时带有不平衡量和初始弯曲的转子的诊断方法进行了研究,认为初始弯曲对转子振动特性的影响可通过与转速同步旋转的激振力来等效。任平珍等[12-13]利用传递矩阵的方法推导了具有热弯曲的转子的振动响应计算方法,并与试验结果进行了对比分析。袁慧群等[14-15]通过有限元法,计算了某高压转子停车后不同时刻的温度分布、热应力及热变形,并据此计算转子的等效热弯矩来模拟热弯曲对转子振动响应的影响。
上述文献针对初始热变形引起的转轴初始弯曲对转子振动响应的影响进行了深入的研究,但这些研究没有考虑转子初始热变形引起的构件质心变化。此外,针对初始热变形对转子系统振动响应的影响规律也缺乏详细研究。本文考虑了初始热变形引起的转子构件的质心变化,并根据初始热变形对转子振动响应的作用效果,建立了相应的动力学方程。通过对方程进行模态坐标变换,分析了初始热变形对转子振动响应的影响规律。
1 初始热变形转子及其动力学方程
1.1 热状态下的转子变形
航空发动机停车后,虽然在流道内可以采取强制换热措施,但是在转子盘-轴结构上仍会有不均匀的温度分布,其典型分布如图1所示。图中以转子左端下表面的温度为基准,对温度分布进行了无量纲化。转子结构的温度分布为涡轮段高于压气机段,截面上下两端的温度梯度由于与实际的材料、构形和连接界面等因素有关,并无显著规律。
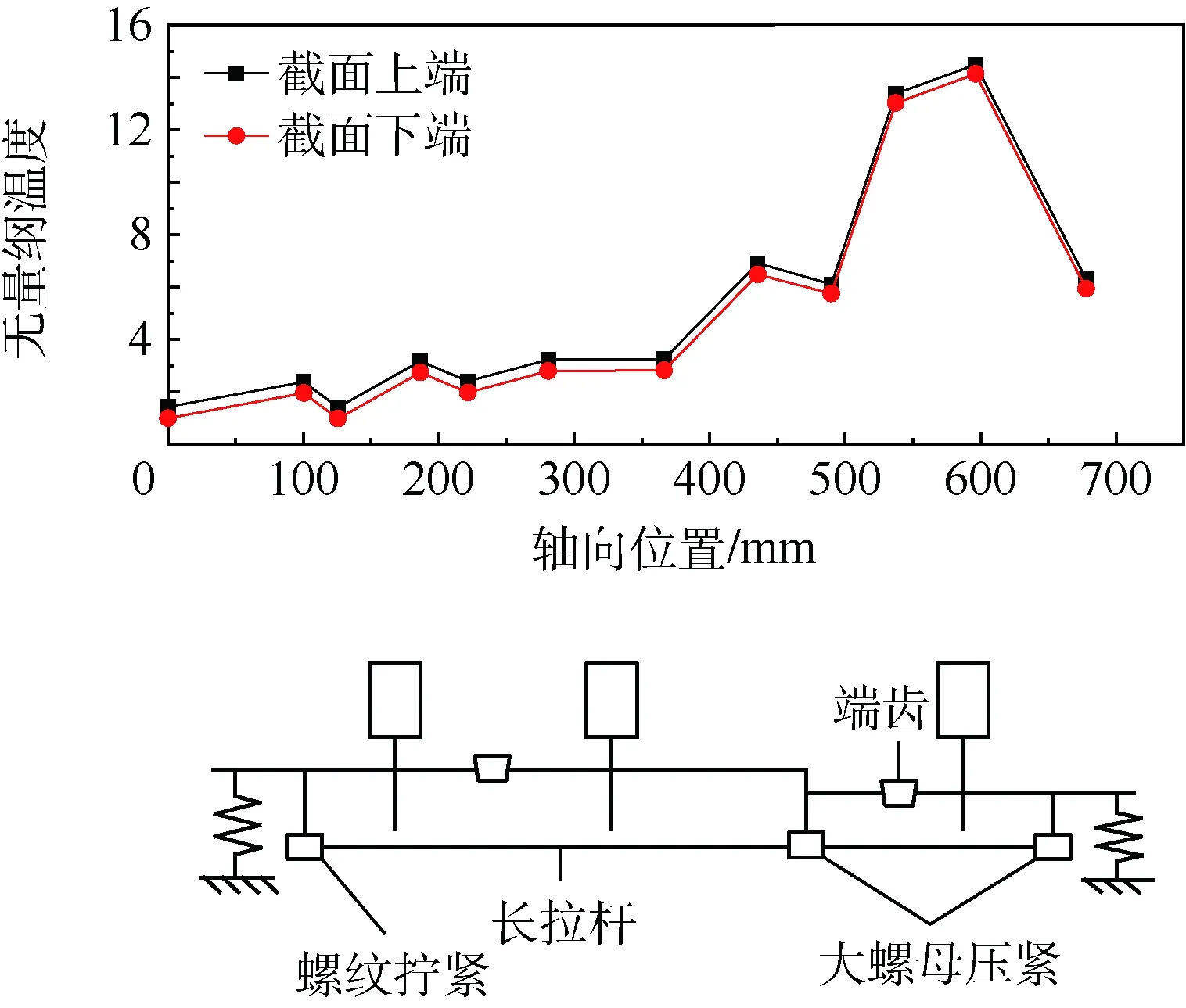
图1 发动机停车后转子温度分布示意图Fig.1 Schematic of rotor temperature distribution after engine shutdown
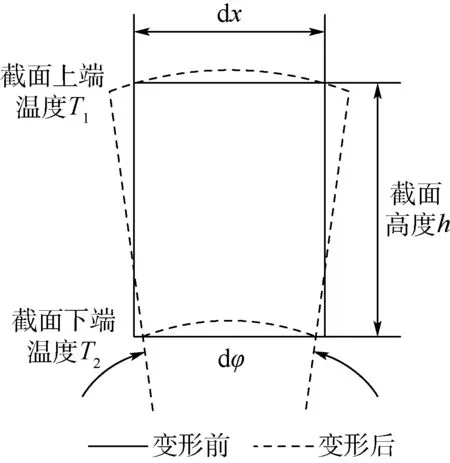
图2 转子微元体热弯曲Fig.2 Thermal bow of a rotor element
假设转子完全冷却后的温度为T0,当发动机进行热起动时,由于温度在径向上分布不均,转子截面上端的温度T1与下端的温度T2并不相同,如图2所示。假设截面温度在竖直方向上满足线性分布(线性分布假设只是为了便于说明温度分布对转子弯曲变形的影响,并不一定与实际情况相同),并设转子微元体的转角为φ,则由几何关系可得
hdφ=α(T2-T0)dx-α(T1-T0)dx
(1)
移项得
(2)
式中:α为材料线膨胀系数;h为转子截面高度。式(2)说明,转子截面径向的温度梯度通过影响截面的轴向变形使转子发生弯曲变形,且温度梯度越大,转子的弯曲变形越严重。此外,变形还与结构的材料、尺寸等因素有关。
转子截面上的温度梯度还会使截面的径向变形产生差异,进而使其形心偏移。如图3所示,由于转轴和轮盘的结构特征、材料热膨胀系数以及连接界面的影响,当转子产生初始热变形后,轮盘的质心不一定与转轴形心线重合,因此,初始热变形后的轮盘会产生附加质心偏移量δ。
设轮盘截面上、下端的位移分别为yd,u、yd,l,转轴截面上、下端的位移分别为ys,u、ys,l,则轮盘和转轴的中心近似为(yd,u+yd,l)/2和(ys,u+ys,l)/2,因此,轮盘的质心偏移量近似为
(3)

图3 轮盘质心偏移Fig.3 Eccentricity of center of mass of a disk
同样,由于转轴和轮盘的结构特征、材料热膨胀系数以及连接界面的影响,当转子产生初始热变形后,轮盘中心线不一定与转轴形心线在轮盘处的切线重合,因此,初始热变形后的轮盘还将产生初始倾斜量τ,如图4所示。
由上述分析可知,转子温度分布不均引起的转子初始热变形主要有3类:转轴弯曲变形、轮盘质心相对旋转中心线偏移、轮盘中心线相对旋转中心线偏移。
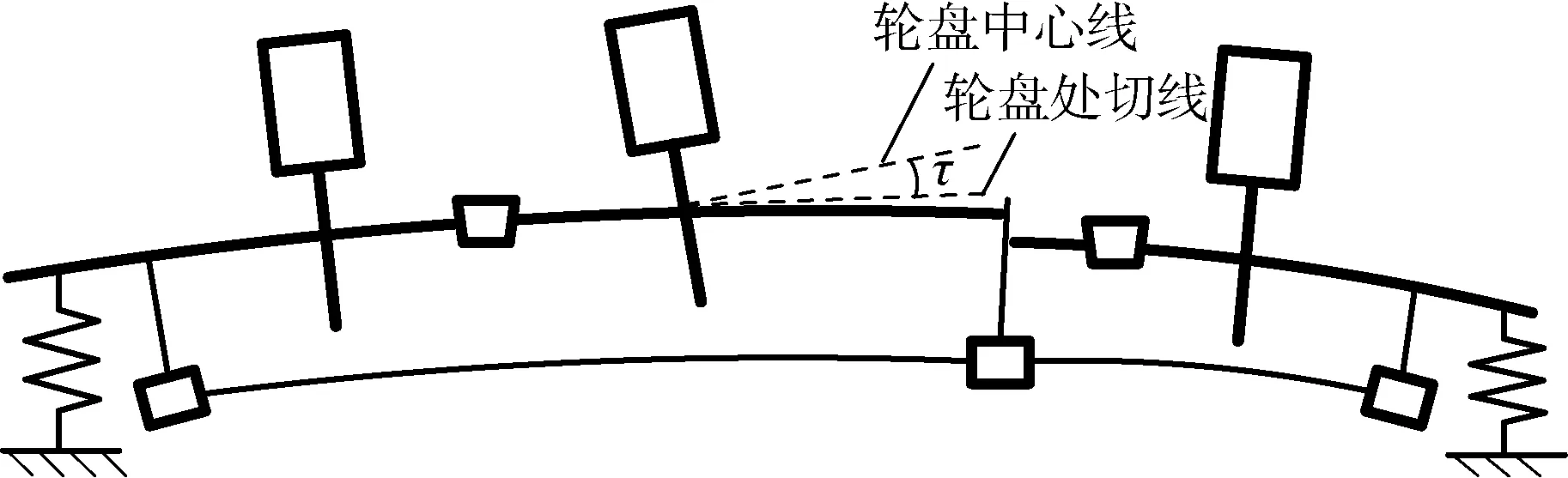
图4 轮盘初始倾斜Fig.4 Initial skewness of a disk
1.2 转子动力学方程
通过有限元法对转子进行振动分析,并采用复数坐标建立动力学方程[16]:
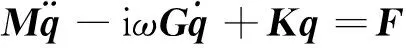
(4)
式中:M为质量矩阵;G为陀螺矩阵;K为刚度矩阵;ω为转子转速;q为转子各节点位移向量,q=[x1+iy1,θy1+iθx1,…,xk+iyk,θyk+iθxk]T;F为作用于转子上的激励。
设转子由初始热变形引起的转轴初始弯曲、轮盘质心偏移和轮盘初始倾斜分别为b、δ和τ。式(4)的物理意义是各节点处满足力的平衡方程。转轴初始弯曲b等效于对转子作用了与转子同步旋转的外力Kbeiωt。轮盘质心偏移δ等效于对转子作用了附加不平衡量ε=m∘δ(“∘”为Hadamard乘积,表示向量各分量相乘),进而引起附加不平衡激励εω2eiωt,其中,m=[…,mk,0,…]T为轮盘质量列阵,mk表示位于节点k的轮盘的质量,δ=[…,δk,0,…]T为轮盘质心偏移列阵,δk表示位于节点k的轮盘的质心偏移量。轮盘初始倾斜会产生陀螺力矩(Ip-Id)∘τω2eiωt,Ip=[…,0,Ip,k,…]T为轮盘极转动惯量列阵,Ip,k表示位于节点k的轮盘的极转动惯量,Id=[…,0,Id,k,…]T为轮盘直径转动惯量列阵,Id,k表示位于节点k的轮盘的直径转动惯量,τ=[0,…,0,τk,…]T为轮盘初始倾斜角列阵,τk表示位于节点k的轮盘的初始倾斜角。将上述表达式代入式(4)可得
(Ip-Id)∘τω2]eiωt
(5)
由式(5)可知,转子的3种初始热变形形式相当于在转子上作用了3种附加激励,且这3种激励均与转子同步旋转。其中,转轴初始弯曲激励Kbeiωt的大小与转速无关,附加不平衡激励εω2eiωt和附加陀螺力矩激励(Ip-Id)∘τω2eiωt均与轮盘的惯性有关,其大小正比于转速的平方。
需要注意的是,对于实际发动机,轮盘的质心偏移和初始倾斜与转轴和轮盘的结构特征、材料热膨胀系数以及连接界面的影响有关,其沿轴向的分布特征难以准确确定。因此,最好通过区间数来描述,即εω2eiωt和(Ip-Id)∘τω2eiωt更准确的表达形式应为εIω2eiωt和(Ip-Id)∘τIω2eiωt,εI和τI表示向量中各元素以区间数表示。
2 初始热变形对转子系统振动响应的影响
2.1 转子动力学方程模态坐标变换
转子在转速为ω时的自由振动方程为
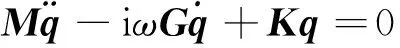
(6)
假设解的形式为q=φeiΩt,Ω为转子的涡动角速度,φ为待求的常数列向量,则转子在转速为ω时的特征方程为
[-Ω2M+ωΩG+K]φ=0
(7)
令Ω=ω,即可求得转子第i阶临界转速ωcr,i及其对应振型φi。对于ωcr,i和φi,显然成立
(8)
由于采用复数坐标时,陀螺矩阵G为对称矩阵,则M-G和K均为对称矩阵。设Φ=[φ1,φ2,…,φn]T,则由振动力学可知,Φ使得式(9)成立:
(9)
(10)
当转子存在转轴初始弯曲激励、附加不平衡激励和附加陀螺力矩激励时,其动力学方程为
εIω2eiωt+(Ip-Id)∘τIω2eiωt
(11)
[-ω2ΦT(M-G)Φ+ΦTKΦ)η=
ΦT[Kb+εIω2+(Ip-Id)∘τIω2]
(12)
即
(13)
因此
(14)
式中:f=[f1,f2,…,fn]T为节点载荷列阵;λi=ω/ωcr,i为第i阶频率比。
因此,转子的振动响应可写为
(15)
将具体的热变形激励的表达式代入式(15)即可分析其对转子振动响应的影响。
2.2 转子初始热变形对振动响应的影响
图5为航空发动机中的典型转子。其临界转速对应的振型分别为平动振型、俯仰振型(统称刚体振型)和一弯振型,且工作转速一般位于刚体振型临界转速以上,靠近一弯振型临界转速。由式(15)可知,当转子分别通过各阶临界转速时,其振动响应近似为
(16)
相应的转子位移和支承反力分别为
(17)
(18)
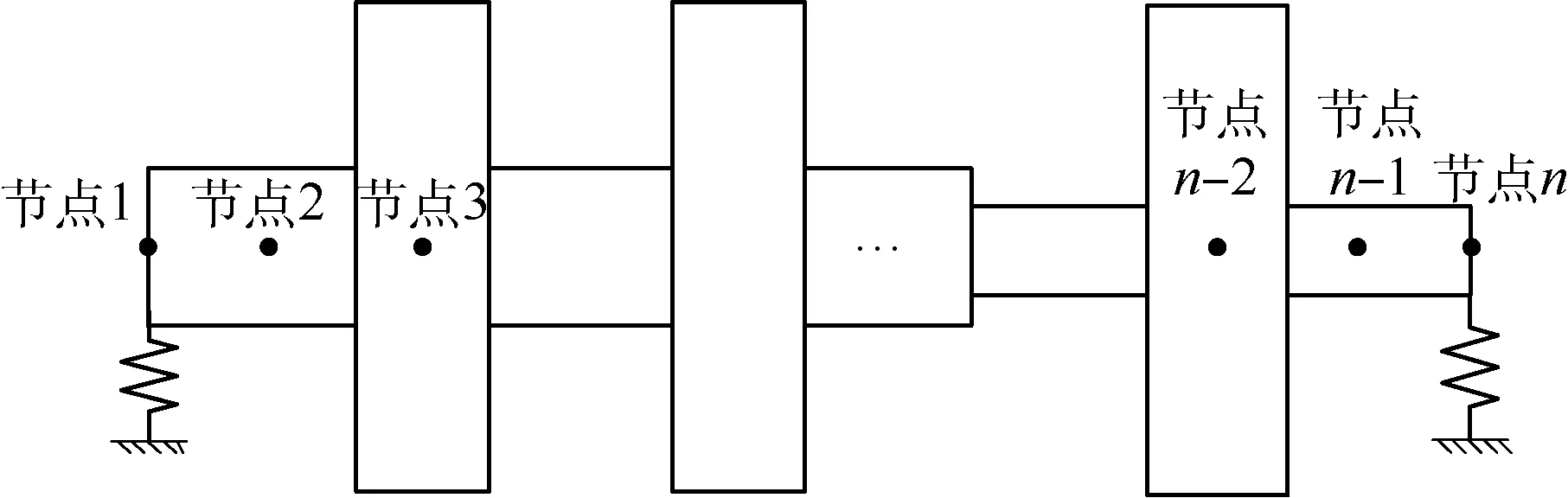
图5 典型航空发动机转子模型Fig.5 A model of typical aeroengine rotors
式中:xi,brg为支点在第i阶振型中的位移;kbrg为支点支承刚度。
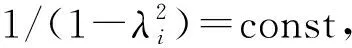
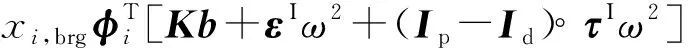

3) 附加不平衡激励εIω2和附加陀螺力矩激励(Ip-Id)∘τIω2沿轴向分布具有非确定性,使得振动响应也具有区间分布的特点,振动响应的这种非确定性可能使转子的支承反力进一步加大。因此,如何更准确地确定附加不平衡激励和附加陀螺力矩激励的分布需要进一步的研究,如在实际工程应用中通过统计的方法进行分析等。
3 典型航空发动机转子振动响应分析
如图6所示,燃气发生器转子为两支点支承的大长径比转子,且工作转速靠近弯曲临界转速,是航空发动机中典型的转子系统。以该实际转子为例,分析其存在初始热变形时的振动响应。
该转子支点跨度为600 mm,最大直径为200 mm,轴承直径为50 mm,压气机材料为TC11,涡轮材料为GH4169。在ANSYS中,采用梁单元BEAM188模拟转子,质量单元MASS21模拟轮盘,弹簧单元COMBIN14模拟支点,节点数为14,单元数为16。
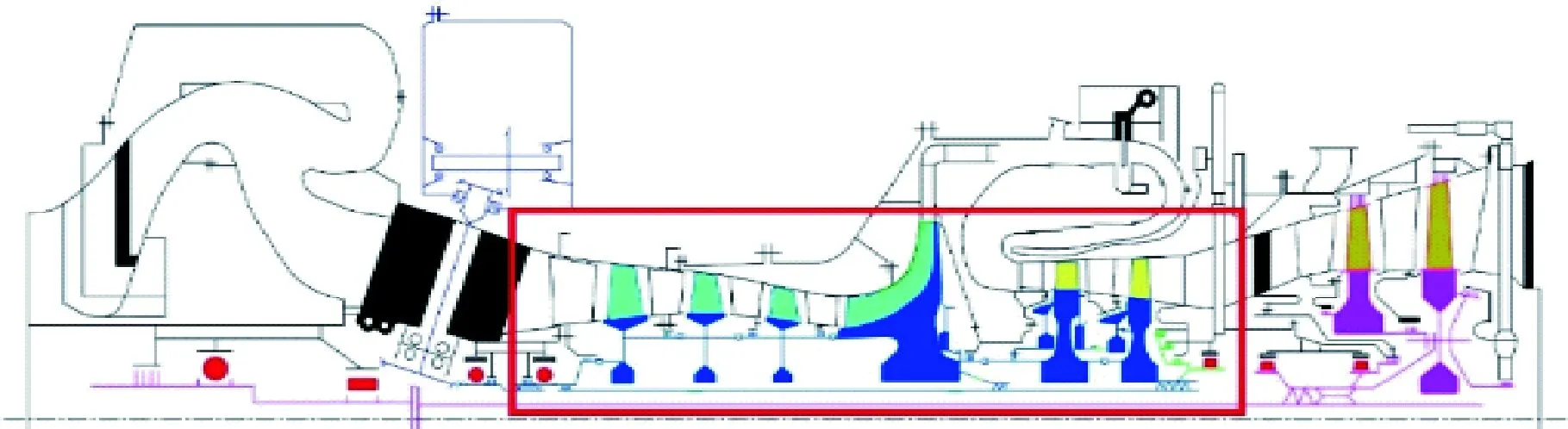
图6 典型航空发动机转子Fig.6 A typical aeroengine rotor
按照1.2节中的热变形转子动力学方程(式(5)),根据转子在给定温度场下初始热变形的有限元计算结果,转轴初始弯曲激励可通过作用于转子轴段中部的径向同步激振力(约5 750 N)来模拟。对于附加不平衡激励和附加陀螺力矩激励,这里仅考虑第一级涡轮盘。根据初始热变形的计算结果,涡轮盘的附加不平衡量约为45 g·mm,考虑连接结构界面接触等不确定因素的影响,以区间数表示不平衡量变化范围[36,54] g·mm(偏差范围取为20%)。同样地,对于涡轮盘的附加陀螺力矩激励,由于难以准确确定数值,根据计算和统计分析取为[0.000 8,0.001 2] rad(偏差范围取为20%)。上述激励的相位均相同。按照上述激励,计算转子系统在不同转速下的振动响应,如图7~图9所示。需要说明的是,由于仅是3种激励的幅值存在区间分布,且3种激励作用的节点均只有1个,因此,转子分别在这3种激励下的振动响应为激励幅值的单调函数,其区间的上/下界可直接由激励幅值的上/下界确定。

图7 转子在初始弯曲激励下的振动响应Fig.7 Vibration response of rotor under initial bow excitation
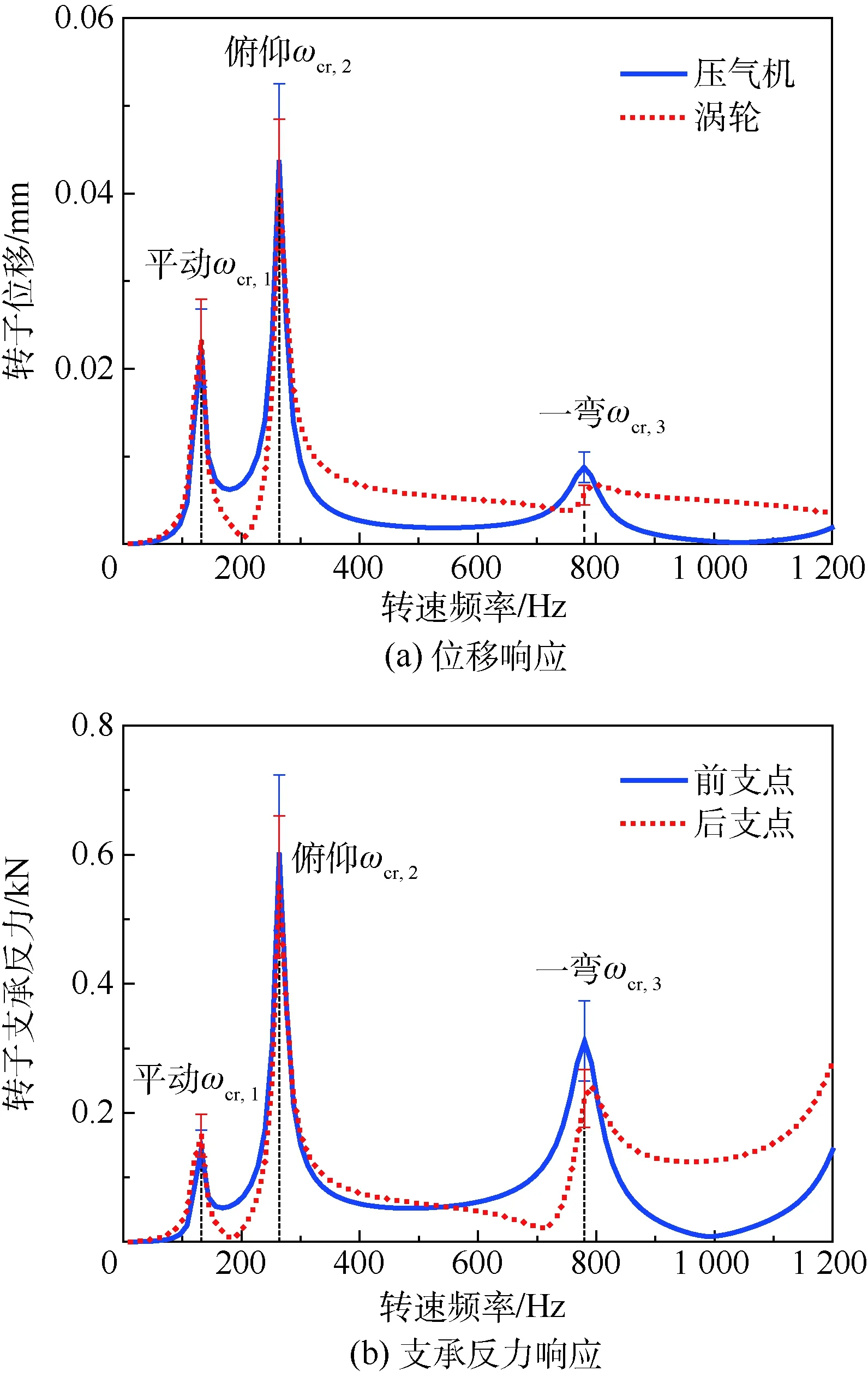
图8 转子在附加不平衡激励下的振动响应Fig.8 Vibration response of rotor under additional unbalance excitation

图9 转子在附加陀螺力矩激励下的振动响应Fig.9 Vibration response of rotor under additional gyroscopic moment excitation
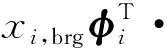
4 结 论
基于理论和仿真,本文主要结论如下:
1) 转子结构系统温度分布不均产生的初始热变形会对转子的振动响应产生影响,根据力学特征可分为:转轴初始弯曲、轮盘质心偏移和轮盘初始倾斜,分别使转子产生转轴初始弯曲激励、附加不平衡激励和附加陀螺力矩激励。
2) 当附加不平衡激励和附加陀螺力矩激励的幅值和方向满足一定的条件时,其与转轴初始弯曲激励在支点处引起的振动响应之和大于仅由初始弯曲激励在支点处引起的振动响应,即与仅考虑转轴初始弯曲的转子相比,附加不平衡激励和附加陀螺力矩激励可能加大支点支承反力的振动响应。
3) 附加不平衡激励和附加陀螺力矩激励的大小正比于转速的平方,其对转子通过频率较低和较高的临界转速时的支承反力均可能有较大的影响,具体影响程度与转子的振型及激励的分布特征有关。而转轴初始弯曲激励大小与转速无关,其主要影响转子通过频率较低的临界转速时的支承反力。
4) 由于航空发动机转子结构材料不同且存在连接界面和几何结构突变,其盘-轴结构系统的初始热变形难以确定,使得附加不平衡激励和附加陀螺力矩激励的大小与相位具有非确定性,进而,转子系统振动响应表现出分散性和区间分布特点。因此,在工程应用中可以对具体结构统计分析其热变形特征。

