基于USM 的岩石薄片模糊图像增强

骆简，滕奇志，何海波

（1.四川大学电子信息学院图像信息研究所，成都610065；2.成都西图科技有限公司，成都610065）

0 引言

在石油地质勘探行业中，通常使用岩石样本制成岩石薄片研究地质油气分布情况。岩石薄片在长期保存中容易受到损坏，而显微成像技术为岩石薄片的数字化信息保存提供了可能，对于后续岩石薄片的研究具有重要意义。由于显微镜视域的限制，小视域下无法观察岩石薄片的整体颗粒分布情况，大视域下无法看清岩石薄片的细节纹理[1]。为了从整体上对岩石薄片进行分析研究，需要在多个连续的视域下采集图像并进行拼接。在图像采集过程中，由于自动聚焦存在误判现象、或因载物台的抖动以及岩石薄片的不平整，导致采集到的某个视域图像模糊或局部区域发虚，最终造成拼接好的全薄片图出现区块状模糊，不能较好地保留岩石薄片信息。为了较好地保留岩石薄片信息，有必要在进行岩石图像拼接之前对模糊图进行复原增强处理。

本文在USM（Unsharp Mask）算法[2]的基础上进行改进，通过Canny 边缘算子提取拥有较少噪声的真实边缘，在Lab 彩色空间[3]的L 通道对模糊图片进行边缘锐化处理，利用动态增益参数抑制噪声的同时达到局部区域图像增强[4]。

1 算法理论基础

1.1 颜色空间的选择

Lab 色彩空间是基于CIE 色彩测量系统的一种色彩模式，其本身基于人类视觉，是独立于硬件设备的，它弥补了RGB 模式依赖于硬件设备特性的缺陷。自然界中任何一点色彩都可以在Lab 空间中表达出来，RGB 所能描述的色彩都能映射到Lab 空间，Lab 比RGB 更适合进行数字图像处理。Lab 空间基于亮度通道L、红绿通道a 和黄蓝通道b 三个通道，各个通道的相关性较弱[3]，有利于后续岩石图像在L 通道的增强处理，保证了岩石薄片的色相不会受到影响。因此，我们将岩石图像从RGB 色彩空间映射到Lab 色彩空间进行处理。而RGB 空间无法直接转换成Lab 空间，需要先转换成XYZ 空间再转换成Lab 空间。

（1）RGB 空间转换到XYZ 空间[5]：

则：

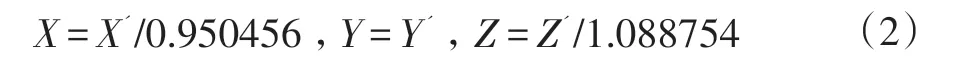
（2）XYZ 空间转换到Lab 空间[6]：

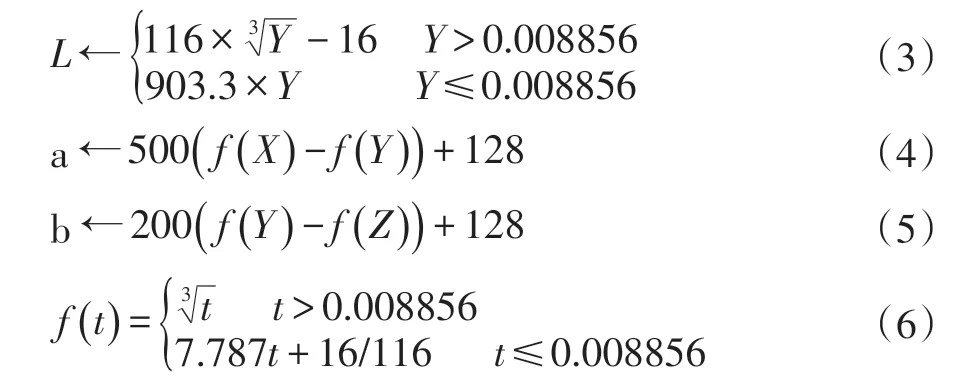
（3）转化Lab 的范围：我们处理的是8 位图，0≤L ≤100，-128 ≤a ≤127，-128 ≤b ≤127，式（7）将其转换到0-255 范围内处理：

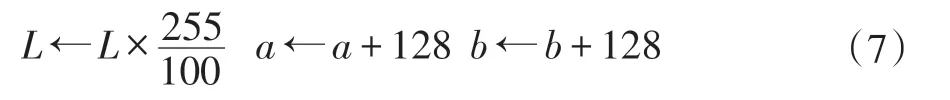
1.2 Canny边缘检测器

Canny 边缘检测算子非常优秀，它能够准确地捕获图像中尽可能多的边缘并且尽可能地滤除图像的噪声产生的假边缘，同时能够准确定位在检测所得边缘的中心，并且只返回一个边缘响应点。因此，Canny 边缘检测具有低差错、易定位、单一响应等特点。Canny 边缘检测算法[2]由下列基本步骤组成：

（1）高斯平滑输入图像

输入图像为s(x,y)，高斯函数G(x,y)由式（8）表示：

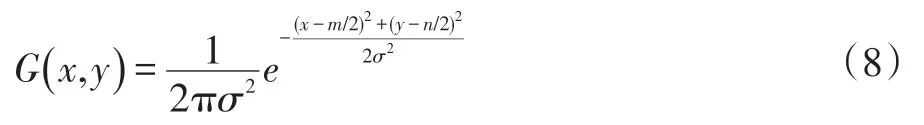
通过式（9）得到高斯平滑后的图像B(x,y)，其中（*）表示卷积运算：

（2）计算平滑图像的梯度幅值和角度

梯度的幅度和角度能反映出每一点处的边缘强度和方向，结合式（10）和式（11）得到幅值M(x,y)和边缘（法向）方向α(x,y)：

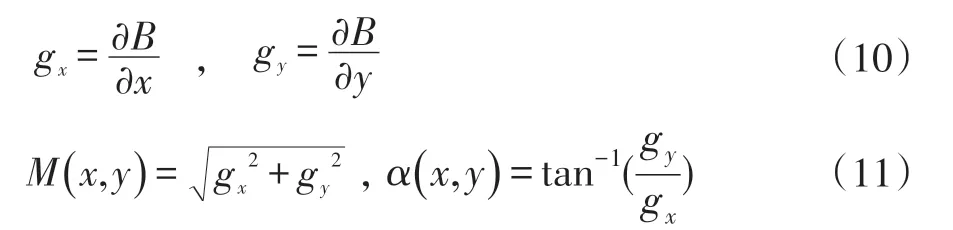
（3）对图像的梯度幅值应用非最大抑制

M（x,y）是使用梯度产生的，其局部最大值周围通常包含更宽的范围，需要使用非最大抑制进行边缘细化。非最大抑制方案详细如下：

①对于通过3×3 领域中间点的边缘，可以划分四个方向：水平d1、垂直d2、+45 度d3、-45 度d4。如表1所示，如果边缘法向方向的范围是从67.5°到112.5°，或从247.5°到292.5°，则我们称该边缘方向为垂直边缘方向；其他方向依此类推。

②寻找最接近α(x,y)的方向dk。

③如果M(x,y)的值同时大于沿dk方向的领域梯度幅度，则令gN( )x,y=M(x,y)；否则，抑制非最大边缘点的M(x,y)，为非最大边缘抑制后的图像梯度幅值。

（4）阈值处理和连接边缘。

Canny 算子采用双阈值对gN进行阈值处理，高阈值TH和低阈值比例一般为2:1 或3:1。

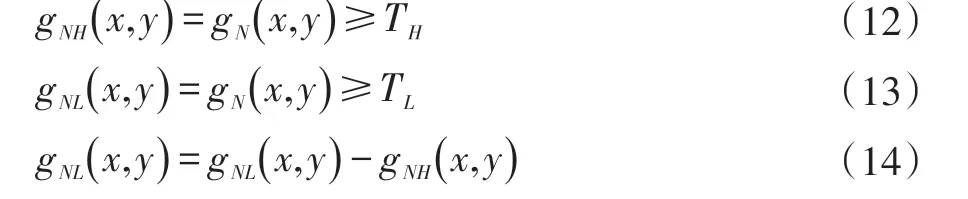
通过式（12）获取强边缘，（13）获取弱边缘。阈值处理后，gNH中的高像素被认为有效边缘像素并对其进行标记。阈值TH决定着gNH边缘缝隙的大小。连续的边缘形成步骤如下：

①在gNH中定位下一个未到达的边缘像素p。

②在gNL将所有弱像素记为有效，用8 连通法连接到p。

③如果gNH中的所有非零像素已到达，则进行第4步，否则转到第1 步。

④将gNL中其他未标记像素认为无效，置零。

最后，将gNL中所有非零像素附加到gNH中，用Canny 算子形成最终的输出边缘图像。

1.3 USM 算法

传统的USM 算法主要用于印刷和出版界[2]，先将原图低通滤波，然后确定原图和低通滤波图的差异，并利用尺度因子放大补偿该差异以增加清晰度。USM 算法详细描述如下：

（1）先将原图s(x,y)卷积一个低通函数w(x,y)得到模糊图blur(x,y)：

表1 边缘方向的划分

（2）将原图与低通图作差就得到非掩蔽模板m(x,y)：

非掩蔽模板包括图像的细节边缘，噪声以及过冲与下冲点等信息。

（3）将上述模板乘以尺度因子k 加到原图上得到锐化图d(x,y)：

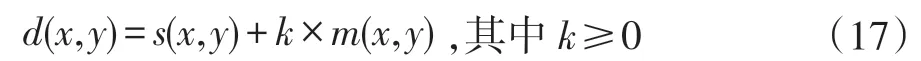
根据线性系统卷积理论[2]，并充分利用模板的对称性，式（15）可简化为加权求和的过程，即卷积运算满足下式：

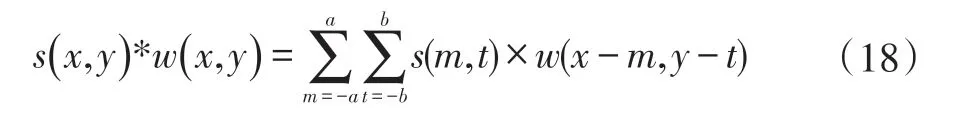
尺度因子k 控制着图像锐化的程度。当k=1 时，对原图像的处理称为非锐化掩蔽；当k ＞1时，对原图像的处理称为高提升滤波；选择k ＜1 则不强调USM 模板的贡献[7]。

2 USM算法的改进

传统的USM 算法是通过原图减去低通滤波图得到需要增强的全局像素区域，增强系数为一固定值k，在增强图像边缘与细节的同时噪声也得到同样倍数的放大；当k 值较大时，增强后的图像会出现负灰度值和超过255 灰度值的像素点，图像局部将被过增强而出现晕轮现象[7-8]。

文献[10]中先计算出3×3 像素领域的局部方差值v，然后对中心像素点进行分类。设置两个正的阈值τ1、τ2和三个常数增益系数1、αdh、αdl，其中τ1＜τ2，1 ＜αdl＜αdh。如果v ＜τ1，将中心像素归为像素平滑区域，将增益系数设为常数1；如果τ1≤v ＜τ2，将中心像素归为中等比对度区域，将增益系数设为常数αdh；如果v ≥τ2，将中心像素归为像素剧变区域，将增益系数设为常数αdl。此算法中，虽然考虑到局部区域的像素变化情况，但是并没有消除大部分噪声增强的影响；阈值和增益系数参数选择对图像的增强也有较大影响。此外，对高分辨率的彩色图像进行处理，需要采用更大的模板和局部区域动态增益。

为了克服传统USM 算法和文献[10]算法的缺点，我们对USM 算法进行改进，采用Canny 边缘算子，在抑制噪声的同时选择性地提取出真实有效的边缘像素[9]；此外，采用动态增益系数来控制高频和细节部分增强的程度，满足图像局部区域动态增强[10]。考虑到图像局部区域的差异性可以用局部标准差LSD 来表征，我们将全局的标准差GSD 与LSD 的比值作为增益系数，保留尺度因子K（本文取值0.24）控制对比度拉伸的程度。改进后的USM 图像锐化的详细步骤如下：

（1）选取大小为（2n+1）×（2n+1）的像素区域，通过式（19）计算局部区域的像素平均值m（i,j），通过区域中间像素f（i,j）的窗口滑动，最终获取原图的模糊图。

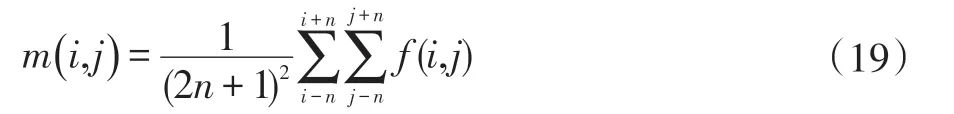
（2）采用两次Canny 边缘算子，适当设置阈值TH和TL，分别提取出原图和模糊图的边缘，分别记为E1(x,y)，E2(x,y)，从而获取需要增强的像素区域E（x,y），即：

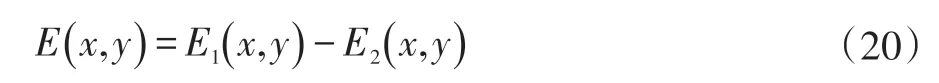
（3）计算(2n+1)×(2n+1)局部区域的标准差σ(i,j)和全局区域的标准差GSD，获得动态增益系数矩阵DG。

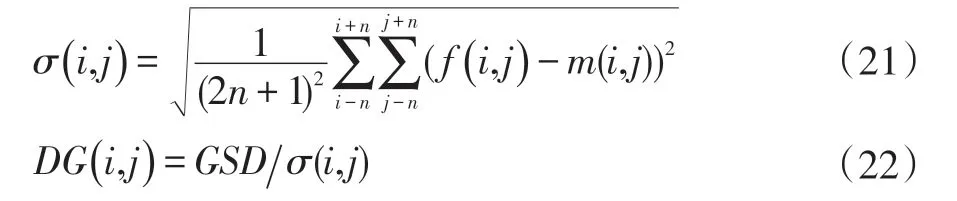
（4）计算增强后的图像d(x,y)，将负灰度值像素置为零，超过255 灰度值像素置为255：

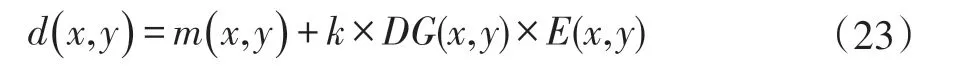
（5）增益系数矩阵DG 由全局区域标准差和局部区域标准差的比值计算得出，反映了局部区域像素与全局区域像素对比度的差异。在图像的边缘或者其他变化剧烈的像素区域，局部均方差比较大，DG 的值比较小才不会导致图像过增强；在图像灰度变化缓慢的区域，局部均方差就会很小，DG 值过大会在增强图像的同时引起噪声的放大，因此需要给DG（i,j）设置阈值。经过大量的实验，阈值为11 时多数图像增强的效果比较好。为了防止缓慢变化区域过度增强而引起噪声 的 放 大，当DG(i,j)＞11 时 对 其 取 值 为1，当DG(i,j)＜=11 时对其取值不变。对于少数增强效果不好的图像，可以调节DG 的阈值，直到对图像增强效果满意为止。

3 实验结果

3.1 图像质量评价指标

为了衡量图像的处理效果，可以利用一些客观分析函数作为评价指标。常见的客观评价指标主要有均方误差（MSE）、峰值信噪比（PSNR）、结构相似性（SSIM）函数[11-12]。

均方误差是计算已处理图和参考图像素差值的均方值，然后通过MSE 值来衡量已处理图与参考图的接近程度，MSE 值越接近于0，表示已处理图越接近于参考图像。MSE 值可通过式（24）获得：

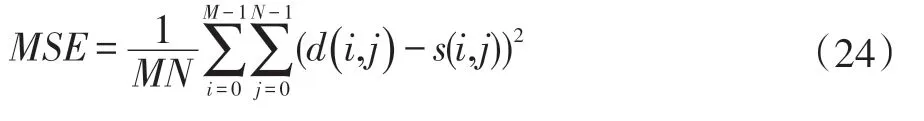
信噪比函数PSNR 一般是用于信号最大值和背景噪声之间的衡量，可以用来评价已处理图像的效果，其值可以结合式（24）、式（25）获得：

其中，d(i,j)为待评价图像，s(i,j)为参考图像，图像的大小是M×N，n 代表处理图像的位深，此处为8。PSNR 的单位为db，值越大代表增强处理后的图像效果越好。

结构相似性SSIM 函数也是一种图像质量评价标准，分别从亮度L(X,Y)、对比度C(X,Y)、结构性S(X,Y)三方面度量图像处理后的质量。

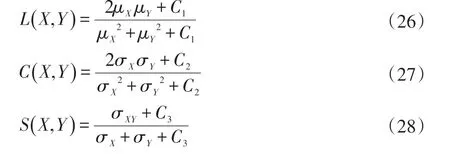
其中，C1=6.5025，C2=58.5225，C3=29.2613，μY表示图像X，Y 的均值，σX，σY表示图像X，Y 的方差，σXY表示图像X 和Y 的协方差：

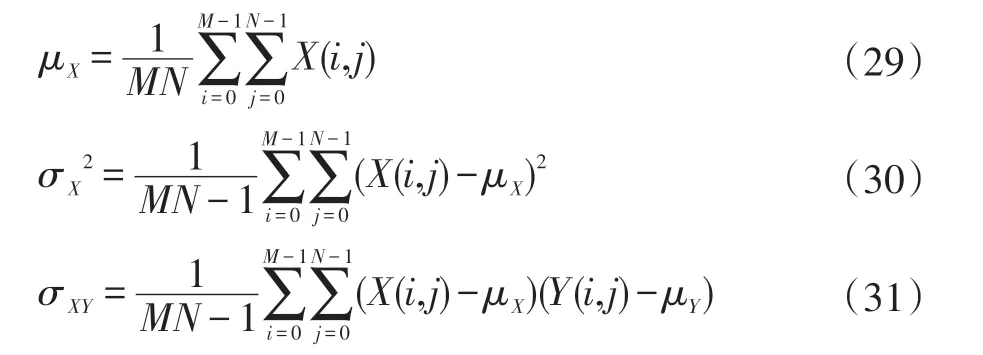
SSIM 值域为[0，1]，值越大，表示处理图效果越好。SSIM 值通过式（32）获得：

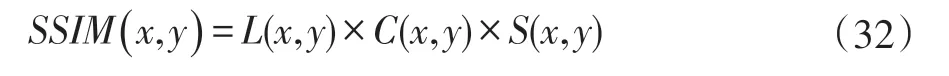
在实际应用中，将图像分成N 块，采用高斯加权计算每一块的SSIM，最后取得平均值MSSIM(X,Y)。

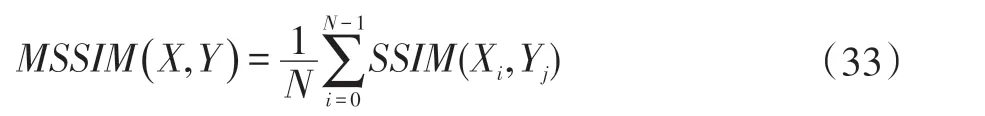
3.2 实验结果分析

为了检验本文改进算法的效果，采用Canon EOS 600D 相机连接显微镜拍摄了多组岩石薄片图进行实验；每一组图都由一张清晰图和3 张失焦模糊图组成，其中清晰图作为参考图像，失焦模糊图作为待处理图像。然后采用传统USM 算法、文献[10]中改进的USM算法、以及本文USM 改进算法对采集的失焦模糊图进行增强处理，最后结合参考图像进行对比分析。本文分别在单偏光和正交偏光模式下处理分辨率为5184×2912 的岩石图像，实验结果如图1、图2。

图1（a）为单偏光模式下采集的岩石薄片某视域清晰图，图1（b）为与图1（a）相同视域采集的失焦模糊图。图1（b）进行传统USM 算法增强处理的图，可以看出，与模糊图相比清晰度有明显的提升，但与原图相比噪声也明显得到放大。图1（d）为对图1（b）进行文献[10]改进USM 算法增强处理图，由于考虑到局部区域的变化情况，清晰度比传统USM 算法增强图有所提高，对比度也得到较好的拉伸，但还是存在明显的噪声；图1（e）为对图1（b）进行本文改进USM 算法增强处理的图，清晰度比传统USM 算法处理图有较大提升，与文献[10]算法处理图对比清晰度变化不大，但却很好地抑制了噪声。

图1 单偏光图像处理结果

图2 正交偏光图像处理结果

图2 （a）为正交偏光模式下采集的岩石薄片某视域清晰图，图2（b）为与图2（a）相同视域采集的失焦模糊图。图2（c）为对图2（b）进行传统USM 算法增强处理的图，与模糊图相比清晰度有一定的提升，但与原图相比噪声也明显得到放大，表现为许多单独的噪点、小的岩石颗粒粘连和部分岩石颗粒边缘出现晕轮。图2（d）为对图2（b）进行文献[10]改进USM 算法增强处理图，与失焦模糊图和传统USM 算法增强图相比清晰度得到更大提高，对比度得到更大拉伸，但噪声也得到明显放大。图2（e）为对图2（b）进行本文改进USM 算法增强处理的图，与模糊图相比清晰度具有明显的提升，与传统USM 增强图相比清晰度也有较大提升，晕轮现象得以消除，岩石颗粒粘连性减弱，岩石颗粒边缘的晕轮被消除，对比度也略微拉伸；与文献[10]算法处理图对比清晰度变化不大，但噪声却明显得到有效地抑制。

以采集的清晰图为参考图，分别计算出失焦模糊图、本文算法增强图、传统USM 算法增强图、文献[10]算法增强图相对于参考图的MSE 值、PSNR 值和MSSIM 值。表2 和表3 为上述两组实验的客观评价函数值的统计结果。

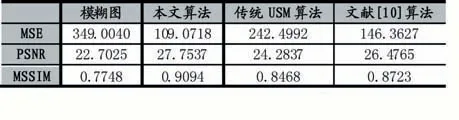
表2 单偏光图处理结果客观评价

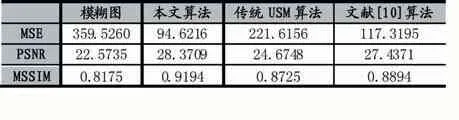
表3 正交偏光图处理结果客观评价

从表中可以看出如下大小关系，MSE 值：模糊图＞传统USM 算法处理图＞文献[10]算法处理图＞本文算法；PSNR 值：模糊图＜传统USM 算法处理图＜文献[10]算法处理图＜本文算法；MSSIM 值：模糊图＜传统USM算法处理图＜文献[10]算法处理图＜本文算法。实验结果表明，本文改进USM 算法在提升图像清晰度的同时能有效地抑制噪声增强，处理图效果更接近于参考图，这与主观分析结果一致。

4 结语

本文提出一个针对岩石薄片图像的锐化算法，通过Canny 边缘算子提取出需要增强的有效边缘部分，采用基于局部标准差的局部区域动态增益函数DG，给DG 设置阈值控制图像增强的范围。实验结果表明，本文算法对模糊岩石薄片有较好的增强效果，可以克服传统USM 算法增强边缘的同时放大噪声的缺点，消除大部分的晕轮现象；克服文献[10]算法不能有效抑制噪声的缺点；可以较好地保留整个岩石薄片的纹理信息以及提高全薄片图的质量。