在GPS 数据挖掘中基于向量自回归的POI 类型转移矩阵规律与预测

李晓娟

（四川大学计算机学院，成都610065）

0 引言

随着人们对各种具有定位功能的智能设备的普遍使用以及基于位置的应用服务在日常生活中的广泛应用，使得每天都会产生大量与位置相关的数据，而对这些数据的分析与探索成为近些年来的研究热点之一。目前已有大量工作从事于基于GPS 轨迹的位置或用户推荐、轨迹模式挖掘、轨迹分类以及异常检测等领域的研究，其中基于GPS 轨迹的POI（Point Of Interest）推荐[1-7]、识别[8-9]以及与其他领域知识相结合的研究[10]更是引起越来越多研究者的关注，但很少有文献专门针对基于GPS 轨迹的POI 类型的变化规律进行研究，这也正是本文工作的主要内容。

基于GPS 轨迹的POI 推荐本质上是一种位置推荐，主要考虑用户所访问位置的地理、时间以及语义因素等来设计各种推荐方法。文献[3,4,7]用基于HITS 模型的系列推荐算法为用户推荐POI 点，通过将每个用户的轨迹按一定规则提取出停留点，例如在地理位置上进行密度聚类或K-means 聚类等，基于某种常识（如用户趋向于访问距离其近的POI 或用户偏好访问某类POI 等）构建用户与POI 间的关系，针对每个用户得到一个关于POI 的排序结果，从而将排序最靠前的k 个POI 点作为推荐结果。其他工作则使用不同方法为用户提供POI 推荐服务，如文献[5,6]采用贝叶斯方法解决POI 推荐问题，文献[1,2]使用传统推荐方法—协同过滤。但这些方法解决的问题本质是对POI 的排序，并未探索多个POI 类型间的相互影响以及变化规律，也没有将研究时间序列的向量自回归模型应用到POI数据挖掘中。

由于室内或城市的一些狭小空间内，GPS 信号较差，甚至没有，存在GPS 数据不够精确的问题，POI 识别模型则是解决如何在GPS 数据不可信的情况下准确识别出现实存在的POI 点的问题。POI 识别模型可理解为一种特殊且复杂的停留点提取方法，虽然其可以准确识别出一个位置在现实中是否是人们都感兴趣的地方。但其同样没有考虑POI 类型间的变化关系，更主要的是没有考虑到多种不同POI 类型间的相互影响关系。

鉴于此，本文考虑多种不同POI 类型间的相互影响，提出新的停留点提取方法用于提取出用户的POI点，还提出基于向量自回归的POI 类型转移演化算法BVAREA，用来探索和发现POI 类型转移矩阵的变化规律，进一步预测未来几期的POI 类型转移矩阵。向量自回归模型是经济学中最常用的模型之一，主要用于对时间序列的分析，本文是第一个将向量自回归应用到GPS 数据挖掘中。而且可将本文工作应用到POI推荐服务中，以便提高推荐的准确性，有助于为用户推荐一些有趣地方，以满足用户对新鲜事物的好奇心和尝试性需求。还可用于POI 识别中，使其能更加准确地识别出现实存在的POI 点的类型，进一步研究用户的行为习惯，从而为用户提供更好的服务与体验。除此之外，与其他学科结合在一起可解决新的问题，如文献[19]将POI 和社会焦虑症结合，对具有社会焦虑症的人们进行研究以发现他们生活规律的不同。因此，对POI 类型的研究具有广泛的应用价值和重要的研究意义。

同时本文在Geolife 数据上进行实验，并与基于AR、MA 以及SES 的模型进行对比，结果表明，对于POI 类型转移矩阵的预测，BVAREA 模型在MEA 和RMSE 标准上均优于其他三个模型，在这两个指标上预测的准确性最大分别可提高约9.23%、14.84%、14.78%、8.05%、14.1%、12.4%。

1 数据预处理

在预处理Geolife 数据前先给出一些相关定义，以便更好地理解接下来的工作。

定义1：（轨迹）一条轨迹Tr=＜P1,P2,…,Pn＞是由最基本的轨迹点Pi=（lat,lng,t）（1＜=i＜=n）按时间顺序构成的，其中lat、lng、t 分别表示地理位置的纬度、经度以及用户到达该位置时的时间戳。

定义2：（带POI 类型的轨迹）已知一条原始轨迹Tr，则 其 对 应 的 带POI 类 型 的 轨 迹TrType=＜PT1，PT2,…,PTn＞，PTi=（lat,lng,t,ty）是一个四元组，其中ty 表示根据GPS 点Pi得到的POI 类型，lat、lng、t 的含义和上面相同。

定义3：（POI 序列）POI 序列集合PoiSeq={PoiSeq1,PoiSeq2,…,PoiSeqN}，PoiSeqi=＜PTS1,PTS2,…,PTSM＞（1＜=i＜=N）是第i 个用户的POI 序列，此序列中的任意一个点PTSj=（lat,lng,ts,te,ty）（1＜=j＜=m）是通过本文提出的新停留点提取方法得到的POI 点，lat、lng、ty、ts、te 分别表示用户i 在访问第j 个POI 点时所在地理位置的纬度、经度、POI 类型以及到达该位置的起始时间和结束时间，M 表示POI 序列中POI 点的总数。

1.1 提取停留点的方法

本文受文献[7]启发，由连续轨迹点一般具有相同或相近的POI 类型，提出一种新方法用来从原始轨迹数据中提取出停留点。新方法涉及到两个参数Nthreod和Tthreod，分别表示在提取出的停留点中包含原始轨迹点的最小个数和最大平均时间间隔。具体过程为，对任一带有POI 类型的轨迹TrType，将第一个点作为临时停 留 点PS，然 后 比 较 相 邻 两 点PTi和PTi+1（1＜i＜|TrType|）的POI 类型是否相同且时间间隔小于Tthreod，若满足条件，则将PTi+1添加到临时停留点PS 中，且PS大小加1。否则保存PS 到停留点列表中，同时生成一个新的空临时停留点PS，将PTi+1添进去。依次类推，直到所有点被遍历完。接着依次判断停留点列表中每个停留点PS 与数量阈值Nthreod的大小，若小于数量阈值，判断PS 的直接前驱和直接后继的POI 类型是否相同，若相同，则将这三个连续停留点合并为一个，否则按公式（1）和（2）计算PS 与其直接前驱和直接后继的avtime 和num，若avgtime 都小于Tthreod，则按这两个值乘积的大小确定PS 应该合并到直接前驱还是直接后继。否则合并到avgtime 小于Tthreod的停留点中，若都不小于Tthreod，则不合并，最后删除小于Nthreod或类型未知的停留点，剩余的停留点便是本文提取出的最终的停留点，也被视之为POI 点，记为PTS。

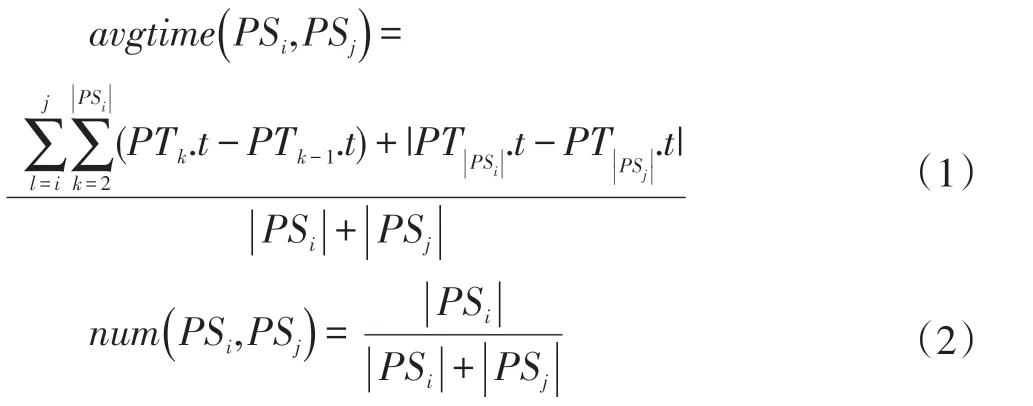
1.2 确定最小POI 点数量的折衷方法

根据上述方法提取出每个用户的POI 点形成一个时间序列，所有用户的POI 序列构成一个集合POISeq，经统计分析，其中POI 点数量大于1000 的POI 序列只有78 个，基于此，本文采用折衷方法来平衡最小POI 点数量和满足POI 点数量要求的用户数量。这是一个循环过程，具体是：将低于1000 个POI点的序列构成集合POISeqS，设初始最小POI 点数量minNum 为0，预计提升minNum 后的新最小POI 点数量newNum 是POISeqS 的平均POI 点数量，则预计提升后用户的下降率和POI 点数量的提升率按如下两个公式计算，若userDroop 大于pointRise，则不提升POI点数量，并退出循环，否则提升POI 点数量，并将min-Num 设置为newNum，进入下一轮循环，直到userDroop大于pointRise 或到达迭代次数才停止循环。

2 POI类型转移矩阵和向量

由于每个用户的行为习惯具有一定的规律性和随机性，本文使用POI 类型转移矩阵序列来刻画用户访问不同POI 类型时的变化规律，POI 类型转移矩阵从一个独特的角度反映出用户访问位置的行为习惯。通过对POI 类型转移矩阵的研究可以间接地了解用户的行为习惯和类型偏好。

定义4：（POI 转移矩阵FTM）假设K 是POI 类型的种类数，存在矩阵FTM，对于矩阵中的任何一个元素ftmi,j（1＜=i，j＜=K）表示用户访问的POI 类型从PTSi转移到PTSj的频次，矩阵FTM 就是所谓的POI 类型转移矩阵。

依据定义3，给定所有用户在t 和t+1 时的POI 类型分布情况，可以生成t 时的POI 类型转移矩阵FTMt。如图1 所示，假设POI 序列的类型种类数是4，则t，t+1，t+2 时的POI 类型分布情况分别是图1（a）～（c），用点的形状表示不同的用户，颜色代表不同类型的POI（即红、绿、蓝、紫分别表示POI 类型0、1、2、3），而（d）和（e）分别表示t 和t+1 时的POI 类型转移矩阵。例如，图1（a）中t 时的蓝色圆点转移为图1（b）中t+1时的红色圆点，对应到图1（d）中FTMt的元素ftm2,0应为1；再如图1（b）中的紫色方块和五角星分别转移为图1（c）中的蓝色方块与五角星，对应到图1（e）的FTMt+1的元素ftm3,2应为2。

为了方便研究POI 类型转移矩阵随时间的变化规律，在此定义了POI 类型转移向量序列。

定义5：（POI 类型转移向量序列FTV）：将上述POI 类型转移矩阵序列中的每个POI 类型转移矩阵FTMi横向展开为一个类型转移向量FTVi，所形成的序列FTV={FTV1,FTV2,…,FTVM-1}被称为POI 类型转移向量序列，其中M 的含义与定义3 相同。

例如，图1 中的两个POI 类型转移矩阵形成一个序列FTM={FTMt,FTMt+1}，按定义5 展开的类型转移向量序列是FTV={（1,0,0,1,0,0,1,1,1,0,0,0,0,0,0,0）,（0,1,0,1,0,0,0,0,0,0,0,1,0,0,2,0）}。若实验数据有限，可考虑将POI 类型转移矩阵的每一行或每一列视为一个向量，利用向量自回归模型学习其相互间的影响，从而间接实现用向量自回归模型学习和预测POI 类型转移向量序列。

图1 POI类型转移矩阵序列

3 向量自回归模型与对比模型

向量自回归模型（Vector AutoRegressive，VAR）：是对单变量自回归模型的推广，它将多变量序列中的每个变量作为其他变量滞后值的函数来构建模型，从而研究多变量时间序列相互间的动态变化规律，即其滞后结构关系，假设Yt=（y1t,y2t,…,ykt）T是一个由k 个内生变量构成的列向量，et=（e1t,e2t,…,ekt）是k 维随机扰动向量，若滞后阶数为p，则VAR 模型（记为VAR（p））表示为：

式中，Yt为t 时的POI 转移向量，Φi是第i 个k×k维的待估计系数矩阵，扰动向量et～N( )0,Ω，其内的变量之间可以相关，但是这些变量不存在自相关，即独立同分布，并且与内生变量也不相关。

在构建向量自回归模型时，重要的一步是阶数的确定，本文采用赤池信息准则（Akaike Information Criterion，AIC）来确定滞后阶数p，取AIC 值最小时所对应的p 值，即为最佳滞后阶数。AIC 的定义如下：

式（6）中的n=k（kp+1）为待估计的参数个数，其中k 为内生变量个数；M 是POI 类型转移向量序列的长度；l 可通过以下等式确定。

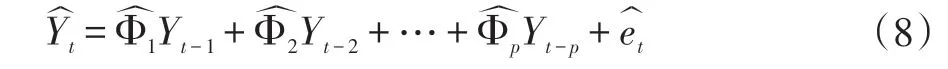
自回归模型（Autoregressive Model，AR）：设yt是POI 类型转移向量中一个分量的时间序列，p 阶自回归过程（AR（p））的形式如式（9）所示，表示序列yt的当前值是p 阶滞后项与随机扰动项et的线性组合，且随机扰动项 et独立于序列 yt-1,yt-2,…,yt-P。与VAR 相比，AR 模型反映出POI 转移向量分量序列的变化只受其自身变化影响的过程，没有考虑其他POI转移向量分量对其变化的影响。针对每个POI 类型转移向量的分量序列，本文分别为其对应的AR 模型筛选出最佳的滞后阶数p，用于说明采用VAR 模型预测POI 转移向量的有效性。

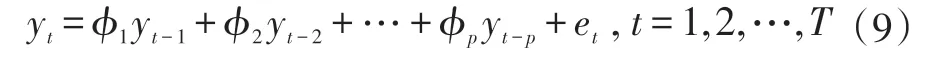
滑动平均模型（Moving Average，MA）：是另一种自相关模式。已知yt是POI 转移向量中一个分量的时间序列，q 阶滑动平均模型（MA（q））的公式化表示如下：

由以上公式可知，滑动平均模型的当前预测值是时间序列过去q 个时期的随机扰动项或预测误差的线性组合。与AR 模型对比，MA 模型中的参数θ 的取值对时间序列的影响没有AR 模型的参数p 那么强烈，所以当存在较大随机变化时，MA 模型一般不会改变时间序列的方向。同理，本文对于每个POI 转移向量分量序列也选取出MA 模型的最佳阶数q。

简单指数平滑模型（Simple Exponential Smoothing，SES）：是一种特殊的加权平均法，是将时间序列的当期观测值与当期预测值经过权重求和得到下一期预测值，特点是为距离预测期较近的序列数据赋予较大的权重，且权重由近至远按指数递减规律下降。公式（11）是简单指数平滑法通项的形式化表示，同时公式（12）给出其递推表示法。

4 基于向量自回归的POI类型转移演化规律

首先根据原始GPS 轨迹数据集中的每条轨迹，通过百度地图的逆地编码得到具有POI 类型含义的轨迹TrType，基于TrType 采用本文提出的停留点提取方法及折衷方法为用户提取出POI 点序列，进而得到随时间不断变化的POI 类型转移向量序列，然后使用向量自回归模型进行建模，从而预测出未来几期的POI 类型转移向量，具体过程如算法为：

算法1：基于向量自回归的POI 类型转移演化算法

输入：经停留点提取方法及折衷方式得到的POI序列集合POISeq={POISeq1，POISeq2，…，POISeqM}，和最小点数minNum，预测期数s

步骤：

1.初始化matrix[][][]//matrix[i][][]是第i 个POI 类型转移矩阵

2.for POISequ ∈POISeq do

3.start ←POISequ.szie—minNum—1//截取距预测期最近的等长序列

4.for PTSi ∈POISequ do

5.if（i==start）then

6. prev ←PTSi

7. elif（i ＞start）

8. matrix[i-start-1][prev.ty][PTSi.ty]++

9.endif

10.endfor

11.endfor

12.for Ti ∈T do

13.FTVi ←matrix[i]//转换POI 类型矩阵为POI类型向量

14.endfor

POI 类型转移矩阵是用一种间接的方式来描述用户的行为习惯和类型偏好，对于某个给定时期的POI类型转移矩阵，表示了用户群从一种POI 类型转移到其他POI 类型的POI 频次分布情况。针对每个用户，按照时间先后顺序排序其访问的POI 点，如果此用户从一个POI 到另一个POI，且这两个POI 是在访问上是相邻的，则更新相应期的POI 类型转移矩阵。具体而言就是，假设一个用户在t0期访问一个类型为tyi的POI，接着在t1期访问另一个类型为tyj的POI，则对应的t0期的转移矩阵中从类型tyi到类型tyj的元素被更新。据此生成定义5 中的POI 类型转移向量，最后使用基于向量自回归模型的POI 类型转移演化算法挖掘出POI 在类型转移方面的演化规律。

5 实验分析

5.1 数据集

本文使用Geolife 数据集，此数据集是由182 个用户在2007 年4 月到2012 年8 月期间生成的，一共有17621 条轨迹，每条轨迹是由含有地理位置纬度、经度以及时间戳的点构成的序列，其中91.5%的轨迹是每1～5 秒钟或5～10 米采样一次。

表1 POI 语义表

如上述描述，本文利用百度地图的逆地理编码API 获取每个原始轨迹点的POI 类型，并按表1 对获取到的POI 类型进行标记，如果获取到的POI 类型不是这四种中的任意一种，则将其标记为5，表示未知类型，得到定义2 所描述的带POI 类型的轨迹TrType后，采用本文提出的停留点提取方法提取出每个用户的POI 点，再用折衷方法筛选出满足要求的POI 序列，最后根据定义4、5 计算出相应的用于各种模型的POI类型转移矩阵序列和POI 类型转移向量序列。

5.2 评价标准

本文将会预测未来s（1＜=s＜=30）个时刻的POI 类型转移向量，所以使用离差标准化方法来归一化向量分量的误差，使其在同一数量级，即具有可比性，具体公式如下：

本文设计两个度量标准MAE（平均绝对误差）和RMSE（标准误差）来衡量VAR 模型的预测性能，分别表示为公式（14）和公式（15），其中的k 表示POI 转移向量的维数。

5.3 参数设置与结果分析

本文依据前期对带有POI 类型的轨迹数据的分析将POI 的类型数设置为4，分别标记为表1 所示。另一个参数便是向量自回归模型滞后阶数的确定，由于AIC 值越小，模型就越能有效地反映变量间的关系，因此选取能够使AIC 值取最小时对应的滞后阶数，如图2 所示，本文VAR 模型的滞后阶数都应设为1。

图2 根据AIC确定滞后阶数

为了验证BVAREA 在POI 类型转移向量上的预测性能，本文将基于AR、MA 和SES 的模型作为其对比方法，这三种模型都是针对单个时间序列的。为了方便描述，将这四种模型简称为VAR、AR、MA 和SES模型。

本文使用这四种模型分别预测接下来30 期的POI 类型转移向量，并与实际的POI 类型转移向量进行对比，分别计算出MAE 和RMSE 指标的值，从而反映出不同模型的预测性能。正如图7、图8 所示，VAR模型的预测性能最好，就MAE 评价指标而言，VAR 模型有28 期的MAE 值都低于AR、MA、SES 模型；对于RMSE 指标，其中有25 期是VAR 模型低于其余三个模型，这说明考虑多序列之间的相互影响对POI 类型转移向量的预测至关重要。VAR 模型与AR 模型相比，在MAE 标准上，VAR 模型的预测性能最高可以提高大约9.23%，最低可提升约1.83%；在RMSE 标准上，VAR 模型预测性能的准确性大约可提升1.16%-8.05%，表明同时考虑多个POI 类型转移向量的分量序列有助于提高预测的准确性。与MA 和SES 模型相比，虽然有时的预测准确性要低于这两种模型之一，但这正体现出POI 类型转移向量分量序列具有一定的随机特性。就MAE 指标而言，VAR 模型在最好情况下可以比MA 模型提高大约14.84%的准确性，比SES 模型可提高约14.1%；根据RMSE 指标，VAR 模型分别比MA 模型和SES 模型提高14.78%和12.4%。

图3 在未来30个预测上不同方法的MAE值

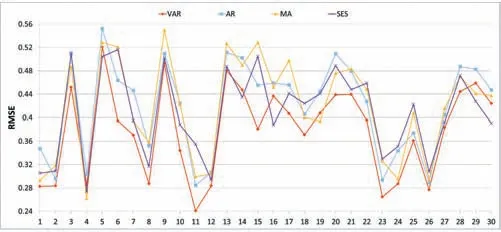
图4 在未来30个预测期上不同方法的RMSE值

6 结语

本文在GPS 数据挖掘中发现现有工作很少有将多个POI 类型的相互影响同时考虑在内，基于此，本文提出一种新的停留点提取方法，目的是从原始轨迹数据中提取出需要的POI 点，同时用一种折衷方式平衡每个POI 序列中POI 点的数量和满足POI 点数量要求的用户数量，然后利用本文提出的基于VAR 模型的POI类型转移演化算法学习POI 类型转移矩阵的变化规律并预测未来几期的POI 类型转移矩阵。最后在真实数据集上进行实验，通过与基于AR、MA 以及SES 模型的对比，说明本文提出方法的有效性。本文是第一个将VAR 模型应用到GPS 数据挖掘中的，同时POI 类型转移矩阵以与之前工作不同的角度来反映用户访问位置的行为习惯和大众偏好，且可将本文工作应用到POI 推荐、POI 识别等有关POI 的领域中。