一种适用于欠压实成因的地层孔隙流体压力预测技术

熊晓军， 黄 劲， 陈 容, LIAO Yiduo， 袁 野

(1.成都理工大学 油气藏地质及开发工程国家重点实验室，成都 610059; 2.Winchester Thurston School, Virginia 22601, U.S.A.)

0 引言

随着油气勘探与开发的逐渐深入，油气藏的地层孔隙流体压力预测日益引起人们的重视，并逐渐成为当今的一个热点问题。地层孔隙压力预测技术自上世纪70年代被成功应用于地震资料的预测研究[1](如等效深度公式法、Eaton方法、比值法、经验公式法、Fillippone方法等)[2-4]。截至目前为止，现在工业界广泛使用的孔隙流体压力预测技术仍是上述方法或其改进方法[2]，仅有几种探索性新方法[3-4]。遗憾的是，针对现今复杂油气藏或页岩气地层，上述地层孔隙流体预测技术往往难以取得较好地实际应用效果。究其原因：①地层孔隙流体压力的成因机制多样化(如欠压实成因、流体膨胀成因、构造作用成因等)；②地震层速度场的影响因素多(如干扰波、叠加速度场的低分辨率等)；③复杂的地质因素影响(如断层对油气藏的地层孔隙流体压力的破坏作用等)。

笔者仅针对欠压实成因机制的情况，采用地震层速度数据体进行地层孔隙流体压力预测。目前，该领域的研究重点在于提高地震层速度场的计算精度，张传进[5]基于常规倾角校正处理后的叠加速度采用DIX公式计算了地震层速度;王英民[6]基于速度场分层的思路对每一个薄层的速度场使用DIX公式求取地震层速度;周东红等[7]对目的层段采用叠后波阻抗反演方法计算地震层速度等。笔者拟在前人研究的基础上，进一步提高地震层速度场的计算，并引入“Fillippone方法+Eaton方法”的组合方法[8]进行三维地层孔隙流体压力预测，从而有效地提高地层孔隙流体压力预测的正确性与可靠性。

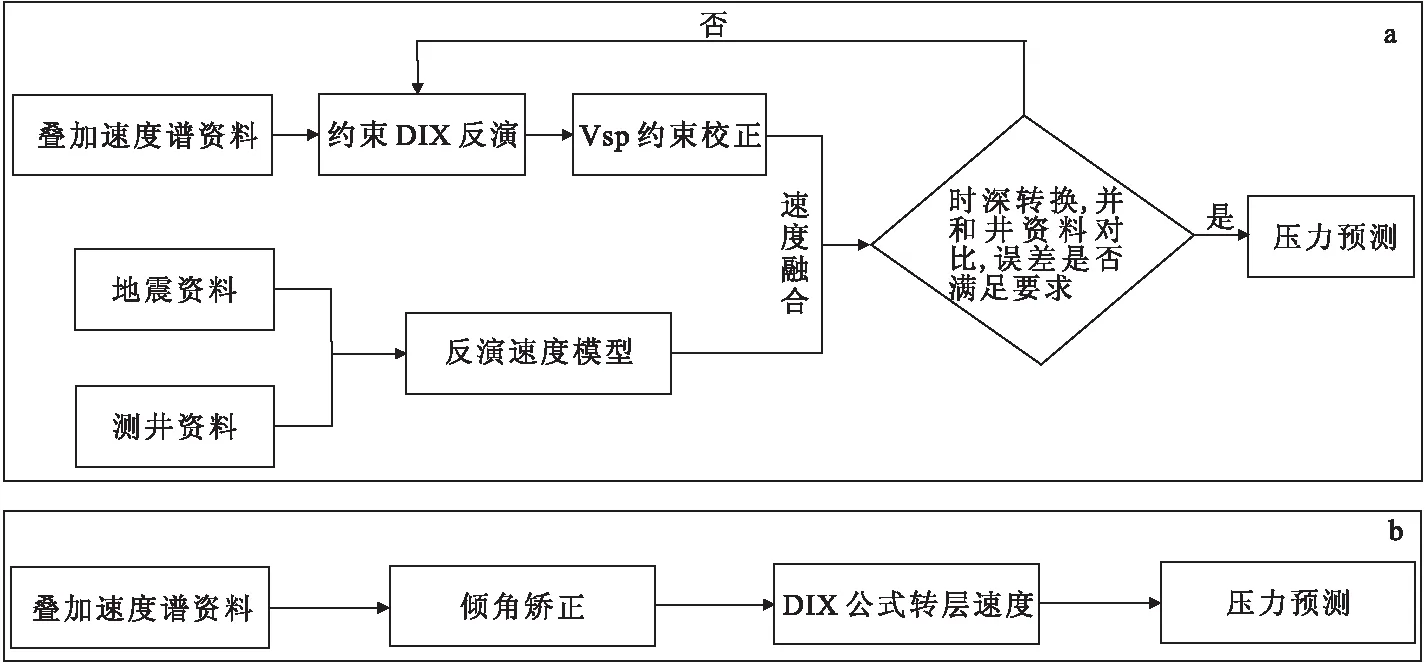
图1 组合速度场建场流程与常规建场方法对比Fig.1 Comparison of combined velocity field construction process and conventional construction method(a)组合速度场建场流程；(b)常规方法建场流程

1 方法原理

1.1 高精度地震层速度场方法

为了提高常规的地震层速度场构建方法的计算精度，我们提出了一种改进的适用于地层孔隙流体压力预测的组合层速度分析方法，该方法的计算流程图如图1所示，其主要包含以下3项步骤：

1)针对浅部地层(无测井曲线的地层段)，采用三维约束DIX反演方法[9]使用叠加速度体、层位数据计算浅部地层的地震层速度体,并利用Vsp曲线约束井半径内速度变化趋势,对速度进行趋势拟合校正。

2)针对中深层地层(有测井曲线的地层段)，采用叠后波阻抗反演方法[10]和叠后三维地震数据体、测井数据、层位数据计算中深层地层的地震层速度。

3)沿着研究区的某一浅部地层分界面，将浅部地层与中深层地层的地震层速度体进行拼接处理，得到一个完整的地震层速度体。

本文方法避免常规方法仅使用叠加速度谱简单插值得出的速度体，充分利用综合使用了三维地震数据、层位数据和测井数据，其获得的地震层速度体目的层分辨率更高，且横向数据相较于叠加速度谱插值计算更可靠。

实践证明基于叠后波阻抗反演得到的地震层速度场获得的地震层速度体比常规基于叠加速度的方法具有更高的纵、横向分辨率。上述计算步骤突出了对测井数据的利用，突出了对基于叠后波阻抗反演得到的地震层速度场的使用。此外，在步骤3中采用沿着某一浅层地层分界面进行2种地震层速度的拼接，其通过判断速度场的纵向变化规律进行整体地震层速度场构建的质量控制(QC)，能获得与研究区地质特征一致的地震层速度场。

1.2 组合模型分析方法

王玉柱等[8]提出了一种新的地层孔隙流体压力预测方法——“Fillippone方法+Eaton方法”的组合模型分析方法，该方法先采用Fillippone方法计算正常压实情况的地层层速度，再采用Eaton方法计算地层孔隙流体压力，其克服了常规方法中正常压实情况下的地层层速度计算的难点问题。

该方法的核心计算公式如下：

1)Fillippone公式。

在水利工程建设中，对工程进行准确有效的造价评估也是极为重要，是工程建设过程中不可或缺的一项。主要是因为工程造价评估触及的方面较多，容易出现问题，从而造成比较严重的后果。因此，一定要建立严谨的造价评估管理制度，对造价评估过程进行全方位的监督与管理，确保在工程建设质量与安全的前提下，减小与实际费用的误差，减少成本的投入，保障水利工程建设能够正常的进行。

Pf=Pov[ (Vmax-Vi)/(Vmax-Vmin)]

(1)

其中:Pf为地层孔隙流体压力；Pvo为上覆岩层压力；Vmax为岩石基质速度；Vmin为岩石孔隙流体速度；Vi为当前地层(计算点)的纵波速度。

2)Eaton方法的计算公式。

Pf=Pov-(Pov-Pw)(Vi/Vn)C

(2)

其中：Pw为静水压力；Vn为地层正常压实情况下的纵波速度；C为调节因子。

式(1)中，当Pf=Pw，有Vi=Vn(正常压实情况下的地层层速度)，即

(3)

图2 研究区过A井的地震层速度剖面Fig.2 Seismic interval velocity profile of well A in the study area(a)基于叠加速度的地震层速度；(b)基于叠后波阻抗反演的地震层速度；(c)组合地震层速度

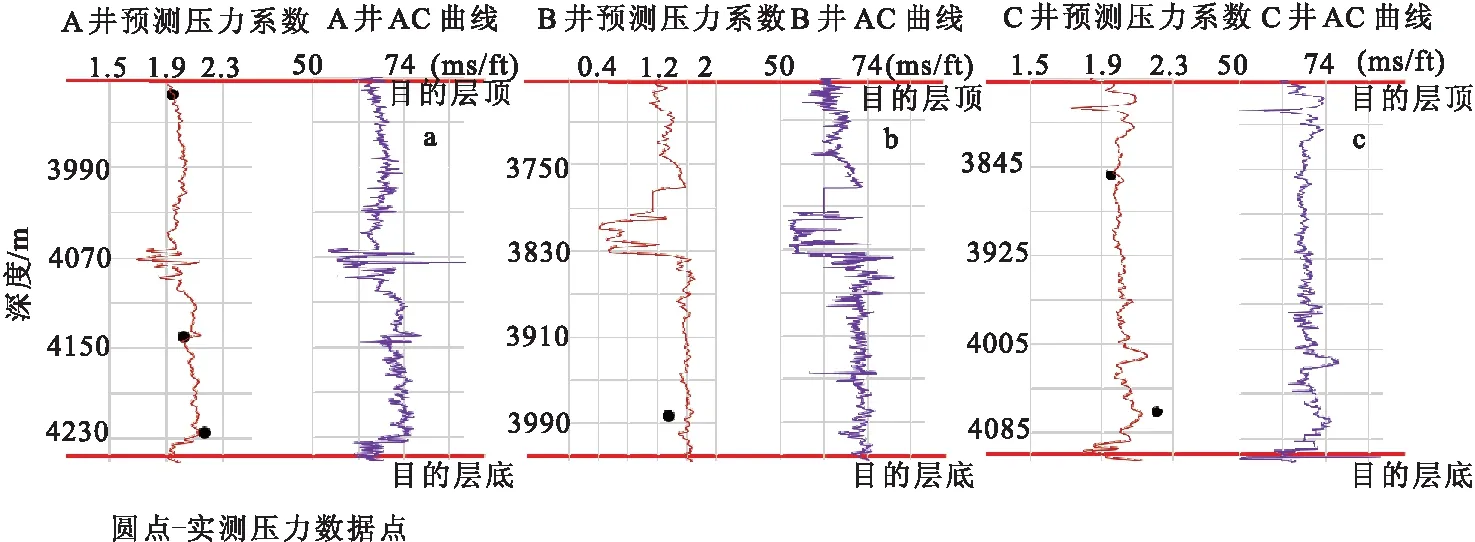
图3 基于测井资料的地层孔隙流体压力计算Fig.3 Calculation of pore pressure based on well logging data (a)A井；(b)B井；(c)C井

根据公式(3)可以计算Vn(正常压实情况下的地层层速度)。

(4)

Pf=Pov-(Pov-Pw)×

(5)

公式(5)是“方法方法”的组合模型分析方法的计算公式，其输入数据前面计算得到的地震层速度数据体，调节因子C由各单井实测点拟合计算得到(本文由实测点拟合得到C值为1.7)，Vmax、Vmin由经验值结和工区测井实测值给出，输出是三维地层孔隙流体压力数据体。

2 实例分析

为了验证本文提出的新方法的应用效果，采用某区的页岩气地层进行地层孔隙流体压力预测的实例分析。研究区的目的层是一套页岩地层，平均埋藏深度4 100 m，共有3口井钻遇该套页岩地层，其中的A井和B井均在目的层钻遇超压地层，实测压力系数高于1.92。为了后续钻探井的顺利开展，非常有必要进行研究区的地层孔隙流体压力预测。

图2(a)是采用三维约束DIX反演方法和叠加速度体、层位数据计算得到的过A井的地震层速度剖面。从图2(a)中可见，其纵向分辨率较低。图2(b)是叠后波阻抗反演方法和叠后三维地震数据体、测井数据、层位数据计算得到的过A井的地震层速度。从图2(b)中可见，其纵、横向分辨率高于图2(a)。图2(c)是沿着图1中的拼接界面得到的组合地震层速度剖面，并且对拼接的地震层速度体进行了三维保边去噪处理[11]消除拼接效应。从图2(c)中可见，地震层速度在拼接层位的纵向方向变化自然，无突变情况，与实际地质情况一致。

基于研究区的3口实钻井的6个实测压力点的数据(图3)，采用“Fillippone方法+Eaton方法”的组合模型分析方法优选公式(5)中的参数C值。先设定C值的搜索范围，再根据计算得到的地层孔隙流体压力值与6个实测点值的均方根误差最小的原则，获得适合研究区的C值(1.7)。表1是采用计算得到的预测地层孔隙流体压力值与实测值的对比分析表，从表1中可知，C井的误差较大，但是6个点的平均相对误差3.74%，能满足实际生产需求。

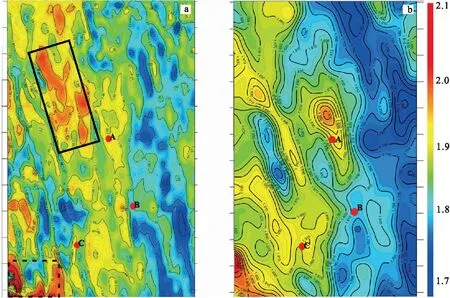
图4 研究区目的层顶界面的地层孔隙流体压力平面图Fig.4 Pore pressure plane diagram at the target layer of the study area(a)改进法压力预测平面图；(b)常规法压力预测平面图

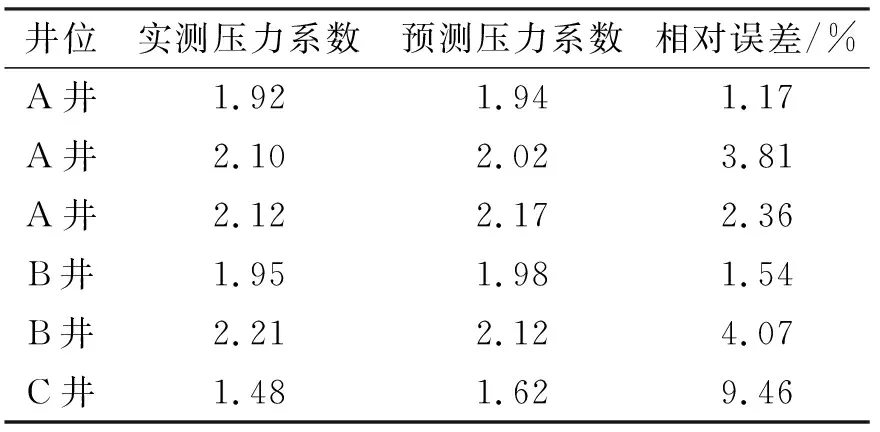
井位实测压力系数预测压力系数相对误差/%A井1.921.941.17A井2.102.023.81A井2.122.172.36B井1.951.981.54B井2.212.124.07C井1.481.629.46

图4(a)、图4(b)分别是采用“Fillippone方法+Eaton方法”的组合模型分析方法计算和采用常规方法计算，得到的研究区目的层顶界面的地层孔隙流体压力平面图，从图4中可见在研究区的西北区域(图4(a)中的黑色实线矩形区域)有异常高压发育，该区域的平面展布形态与研究区的地质分析的页岩“甜点”区域一致，即超压更有利于页岩气的聚集。此外，图4(a)中西南区域(黑色虚线矩形区域)的红色高地层孔隙流体压力值区域受地震资料覆盖次数低和低信噪比的影响，预测结果不可靠。而图4(b)中常规方法虽然能勾画出工区压力大致走势，但是其分辨率较低无法准确刻画出页岩”甜点”区域。

3 结论

1)笔者提出改进的适用于地层孔隙流体压力预测的组合层速度分析方法,突出了对测井数据的利用，并突出了对基于叠后波阻抗反演得到的地震层速度场的使用，能获得高精度的地震层速度数据体。

2)我们提出的一种适用于欠压实成因的地层孔隙流体压力预测技术，先采用组合层速度分析方法计算地震层速度数据体，再采用“Fillippone方法+Eaton方法”的组合方法计算地层孔隙流体压力，综合利用了三维地震数据、叠加速度体、测井数据、层位数据和实测压力数据等多源信息，方法理论较常规方法更完善。

3)实际资料的计算结果表明，采用本文提出的适用于欠压实成因的地层孔隙流体压力预测技术获得的地层孔隙流体压力预测值与实测值误差较小，且有效地预测了研究区的地层孔隙流体压力的超压区域，对研究区后续的勘探与勘探具有重要的指导意义。