基于矩阵的多维关联规则算法在烟叶复烤配方的应用研究∗

王萝萍 唐兴宏 钱颖颖 马永凯 于春霞 秦玉华

（1.云南中烟工业有限责任公司技术中心 昆明 650024）（2.青岛海大新星计算机工程中心 青岛 266071）（3.青岛科技大学信息科学技术学院 青岛 266061）

1 引言

关联规则［2］是一种很好的挖掘烟叶间组合和搭配的方法。自从R.Agrawal等［3］于1993年提出关联规则挖掘问题后，众多的学者对该问题进行了大量的研究，其中最有效和最有影响的是Apriori算法。它以递归统计为基础，生成频繁项集，易于实现，但该算法每次寻找K频繁项集都要扫描一次事务数据库来获取候选项集的支持度，频繁的I/O操作严重影响算法效率。同时，为了生成候选项集，在连接步骤需要大量的比较，非常耗时［4］。针对Apriori算法的不足，已经有学者给出了不同的改进方法。FP-Growth算法［5］采取增长模式的递归策略，避免了候选项目集的产生，但在挖掘过程中，如果大项集的数量很多，并且由原数据库得到的FP-tree的分支很多，该算法需构造出数量巨大的conditional FP-tree，不仅费时而且要占用大量的空间，挖掘效率较低。Apriori-sort算法［6］用折半插入排序思想对Apriori算法进行了改进，但当事务数据库非常大时，查找插入点同样非常耗时。目前在提高关联规则效率的研究中，大多采用基于Hash函数技术及各种剪枝策略［7］，但当支持度比较低时，算法效率仍不能较好的提高［8］。此外，目前大部分关联规则算法主要是针对单维数据挖掘，仅包含多次出现的单个谓词［9］，而烟叶配方组合规律的挖掘需考虑产地、等级、部位等多个属性，因此需将单维关联规则数据挖掘扩展为多维关联规则挖掘［10］。

针对上述问题，本文在经典Apriori算法的基础上，提出了一种基于矩阵的多维关联规则改进算法并将其应用到烟草复烤模块配方数据挖掘中，该方法通过构造多维事务矩阵［11］，减少了扫描数据库的次数，同时不断通过剪枝、剔除冗余事务对矩阵进行压缩，提高了挖掘效率，从而有效地挖掘出历史配方中烟叶的搭配和协同信息。

2 Apriori算法简介

关联规则挖掘是从大量数据中挖掘项集之间的相关联系［12］。其相关定义如下：

定义1项与项集［13］：数据库中不可分割的最小单位信息，称为项目，用符号i表示。项的集合称为项集。设集合I={i1,i2,…,ik}是项集，I中项目的个数为k，则集合I称为k-项集。

定义2事务：设I={i1,i2,…,ik}是由数据库中所有项目构成的集合，一次处理所含项目的集合用T表示，T={t1,t2,…,tn}。每一个ti包含的项集都是I子集。

定义3关联规则：形如 X⇒Y的蕴含式，其中X,Y分别是I的真子集，并且X∩Y=Ø。X称为规则的前提，Y称为规则的结果。关联规则反映X中的项目出现时，Y中的项目也跟着出现的规律。

光学透雾使用透雾镜头配合支持透雾的摄像机组合成的光学透雾组合，呈现最为明显的效果，光学透雾能够观察到雾气后方的景物，具有层次和立体感。

定义4支持度（Support）：事务集中同时包含的X和Y的事务个数与所有事务数之和之比，记为support（ X⇒Y ），即：support（X⇒Y ）=support X∪Y=P(XY)。

定义5置信度（Confidence）：事务集中包含 X和Y的事务集数与所有包含X的事务数之比，记为confidence（X⇒Y ），即

定义6最小支持度与最小置信度：通常用户为了达到一定的要求，需要指定规则必须满足的支持度和置信度阈限［14］，当support（X⇒Y）、confidence（X⇒Y）分别大于等于各自的阈限值时，认为X⇒Y是有趣的，此两个值称为最小支持度阈值（min_sup）和最小置信度阈值（min_conf）。其中，min_sup描述了关联规则的最低重要程度，min_conf规定了关联规则必须满足的最低可靠性。

定义7频繁项集：设L={l1,l2,…,ln}为项目的集合，且 L⊆I,L≠Ø，对于给定的最小支持度min_sup，如 果 项 集 L的 支 持 度support(L)≥min_sup则称L为频繁项集。

定义8强关联规则：support（ X⇒Y）≥min_sup且confidence（X⇒Y ）≥ min_conf，称关联规则为强关联规则。

Apriori算法的思想是，扫描一次数据库，找出频繁1-项集的集合。该集合记作L1。L1用于找所有可能的候选2-项集的集合C2，用L1和C2，找出频繁2-项集集合L2，而L2用于寻找候选3-项集的集合C3，用 L2和C3，找出频繁3-项集集合L3。如此下去，直到不能找到频繁k-项集。其中找每个Lk需要一次数据库扫描。最后用所有频繁项集产生强关联规则。生成候选项集主要有两个步骤：连接和剪枝［15］。连接操作是一种类矩阵运算，即Lk-1与Lk-1遵循一定的规则连接产生可能的候选项。剪枝操作是去掉无意义或者没有必要的中间结果。

3 基于矩阵的多维关联规则改进算法

本文提出的基于矩阵的多维关联规则算法流程图如图1所示。

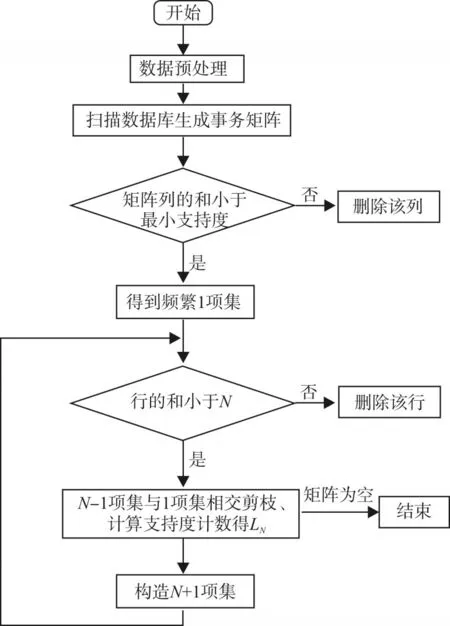
图1 算法流程图

具体实现过程描述如下：

Step1：多维数据预处理。算法在处理数值型数据时，采用分区的方式将数据转化为布尔型数据。

Step2：以事务数据库中的事务为数据源，用Ik表示事务数据库中的项，Tj表示事务数据库的事务，以事务Tj为行，项Ik为列构造矩阵。该事务中若有此项则填1。当没有此项时填0，扫描事务数据库，构造一个布尔型矩阵A。若该事务数据库有m个事务n项，则构造的布尔矩阵为一个m行，n列的布尔矩阵。

Step5：求频繁2项集。当 sum（Tj）<2时则该事务不能为频繁2项集做贡献，则从矩阵A1中删除该事务；将矩阵A1中的列两两相交，例如项 I1，I2将该两项取交集后计算支持度计数为：

当 sup_count（ I1∩I2）≥ min_sup时，将｛I1，I2｝添加到频繁2-项集L2中。用筛选后的事务为行，L2中的项为列，得到新的矩阵A2。

Step6：求频繁3项集。当 sum（Tj）<3时则该事务不能为频繁3项集做贡献，则从矩阵A1，A2中删除该事务；将矩阵A1与A2中的项两两取交集，在求支持度计数之前，先检查该项的所有2项子集是否在L2（类推为Lk-1）中。如果是则求支持度计数，如果不是，则丢弃该项。如I3、（I1，I2）将该两项取交集后得到（I1，I2，I3），检查（I1，I2），（I1，I3），（I2，I3）是否都在 L2中。如果是则求支持度计数：

当sup_count（I3,(I1,I2)）≥min_sup时，将｛I1，I2，I3｝添加到频繁3-项集L3中。用筛选后的事务为行，L3中的项为列得到新的矩阵A3。

Step7：循环判断执行Step5，直到求频繁K项集时，当Ak+1=Ø时结束循环，则得到最大频繁项频繁K项集。

4 实验及结果分析

4.1 实验数据

为了验证本文方法在模块配方规则挖掘方面的有效性，选取了云南中烟技术中心不同年度120个相近复烤模块配方数据。表1为某模块的配方数据。可以看出，该模块配方包含7个单料烟叶，配方人员进行配方维护和设计时，需考虑烟叶产地、年度、等级、品种、比例等综合信息。

4.2 数据处理

本研究主要考虑对2维的烟叶配方数据进行挖掘研究。将表1烟叶数据根据产地、品种、等级、年度等信息进行编号，如2015年产地C1、品种K326、等级CO2的烟叶编号为P15001，这样烟叶模块配方信息可降为2维：等级比例和烟叶编号。

等级比例根据经验划分为3个等级：<10%为低、10%-20%为中、＞20%为高，分别用数字0、1、2表示。在编号最前面添加数字表示此烟叶在复烤配方模块中的比例，如0P15001、1P15001、2P15001分别代表编号为P15001的烟叶在配方模块中所占比例分别为低、中、高。

表2为处理过的120个复烤模块，共356个烟叶的事务矩阵M。其中每一个烟叶用三列表示比例的高、中、低，因此构成的事务矩阵M为120行1068列。

表2 事务矩阵M

4.3 数据挖掘结果及分析

为减少生成的规则数，本研究定义了最小支持度阈值（Minimum Suppport Threshold）为 0.2，最小置信度阀值（Minimum Confidence Threshold）为0.5，满足条件时才会作为一条规则。同时为提高关联规则的准确性还引入了作用度Lift。Lift计算如下：

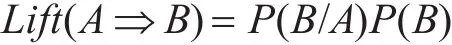
只有Lift大于1时，该规则将被认为有效，即规则中两事物正相关。

表3为对120个历史配方模块挖掘的部分结果。其含义如下：对于规则A⇒B，支持度表示同时含有某两种烟叶A、B的概率，置信度表示在包含A烟叶的情况下，同时含包含B烟叶的概率。

表3 烟叶关联规则表

通过对挖掘出的所有烟叶搭配规则可以看出，配方模块中同时包含编号为D15063和D15052的烟叶概率最大 Support(D15063⇒D15052)=31.58%，同时，它的置信度也是最高的Confidence(D15063⇒D15052)=83.86%，表明在实际配方模块中，该两个烟叶的搭配比较合理，并且D15063的比例应在20%以上，D15052的比例在10%与20%之间。其次是D15089和D15257烟叶组合Support(D15089⇒D15257)=27.31%，说明该两个烟叶搭配也比较合理，从挖掘的结果可以看出，D15089的比例应在10%与20%之间，D15257的比例则应小于10%。上述结果与配方人员的经验完全一致，说明该挖掘结果可将历史配方数据中隐含的诸多配方人员的经验知识提取为规则表示形式，从而有效指导实际复烤模块配方维护工作，减少配方研发人员的工作量。

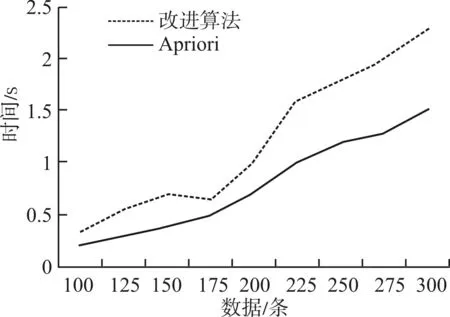
图2 算法效率对比

4.4 算法性能比较

图2 为本文方法与经典Apriori算法的运行效率比较。可以看出，本文所提出的算法运行效率明显高于Apriori算法，特别在数据量增多的情况下算法效率提高较为明显，可以更高效地进行关联规则的挖掘。

5 结语

本文在传统Apriori算法的基础上，针对烟叶复烤配方模块多维数据挖掘的需求，提出了一种基于矩阵的多维关联规则改进算法，该算法只需要扫描一次事务数据库，避免了传统Apriori算法多次扫描事务数据库的缺陷，有效提高了挖掘效率。在对烟草复烤模块历史配方数据挖掘中，能有效地将配方数据中隐含的配方专家的配方维护行为规律提取为规则表示形式，并且全面地考虑烟叶间的优化组合，减少了配方研发人员的工作量，该方法可以更高效地指导实际配方设计和维护工作，为模块配方的优化和完善提供新的理论依据和方法。