基于简化模型的B柱抗弯性能优化*

莫易敏 刘青春 吕俊成 沈 鹏 夏 青 李铁铮

(武汉理工大学机电工程学院1) 武汉 4300701) (上汽通用五菱汽车有限公司2) 柳州 545007)

0 引 言

在车顶挤压和侧面碰撞中，B柱作为主要的承载部件，抗抵车顶结构和侧面结构发生的大变形，对保护乘员安全和提高车身车顶及侧面结构的耐撞性能起到重要的作用[1]，因此，考虑到B柱耐撞性能对乘员安全和车体变形的影响研究至关重要，B柱的抗弯性能研究一直是车辆侧面碰撞研究中重要课题.近些年，学者对B柱结构优化方面做了相关研究.谭耀武[2]使用Hypermesh和Hyperstudy软件对B柱拼焊板及内板的结构进行优化设计.曲晓庆等[3]运用CAE仿真通过对改变B柱材料进行优化设计.目前，B柱的结构优化主要集中在截面尺寸、材料及加强板中使用拼焊技术或改变拼焊位置等.然而，上述优化主要是改变B柱一个因素或者两个因素，针对B柱多个因素的优化分析较少.综上所述，提出对B柱各板厚度和截面尺寸等多个变量进行多目标优化，在提高侧面碰撞抗弯性能的前提下兼顾轻量化要求.

由于B柱结构复杂，不仅给试验带来困难，还增加其仿真难度.在试验方面：需要设计人员反复改变B柱的截面尺寸、各板厚度进行大量实验研究，增大制造工艺难度与成本.在仿真方面：B柱呈曲面形状，存在内孔等，给其仿真模型参数的修改增加难度，增大工作量和计算时长.针对上述所存在的问题，有必要对B柱进行等效的简化处理，提出了一种简化方法，将B柱简化为带有加强板的单帽梁结构.在三点弯曲工况下将B柱和单帽梁简化模型进行对比，验证单帽梁模型的可行性.其次将单帽梁的简化模型与仿真模型进行对比，验证单帽梁仿真模型的有效性.

将带有加强板的单帽梁作为研究对象，采用最优拉丁超立方方法对单帽梁的加强板厚度、内板厚度、外板厚度，以及加强板到外板的距离四个设计变量进行抽样，根据样本点对仿真模型进行修改及有限元计算，并建立设计变量与设计目标函数之间的二阶响应面模型.以平均加载力和质量为设计目标，运用多目标优化算法中的非支配排序遗传算法NSGA-Ⅱ进行优化，得到设计目标的Pareto前沿.从中找到较优的单帽梁几何参数，带入仿真模型与原始模型进行对比验证.最终在改善侧面碰撞安全性的同时满足轻量化要求.

1 B柱结构简化模型分析

1.1 研究对象

B柱是侧围零部件中最为关键的部件之一，其耐撞性往往决定了整车的侧面碰撞安全性能[4].在汽车发生侧面碰撞时，考虑乘坐姿势，乘员腹部器官和胸部器官二者当中，腹部器官的损伤对生命的威胁程度相对较低，因为腹部主要是肠，胃等软质的器官，可以承受外界破坏的能力较高.而有研究显示碰撞中的侵入速度对车内乘员肩部和胸部的变形影响比腹部更加显著.在侧面碰撞过程中，发生弯曲受损最严重的部位即是B柱中部位薄弱的环节，对应车内乘员肩部和胸部，同时B外板的上端与顶边梁连接、下端与门槛相搭接，因此本文将B柱最薄弱环节作为研究部位.

1.2 B柱结构l简化模型

由于B柱结构复杂，整体呈曲面，包含孔洞和倒角等.不仅给试验带来困难，还增加其仿真难度.增大工作量与总体成本.B柱是以单帽梁结构为基础模型，再根据实际的结构布局、避让需求和造型设计等原因，在基础模型的基础上改进结构，如增加倒角、圆孔、凸台等.为了对侧围结构件的耐撞性进行研究并优化，将B柱简化为带有加强板的单帽梁结构，B柱简化后的单帽梁结构见图1，研究单帽梁内外板厚度、加强板厚度以及加强板到外板距离这四个因素对侧面碰撞抗弯性能的影响.

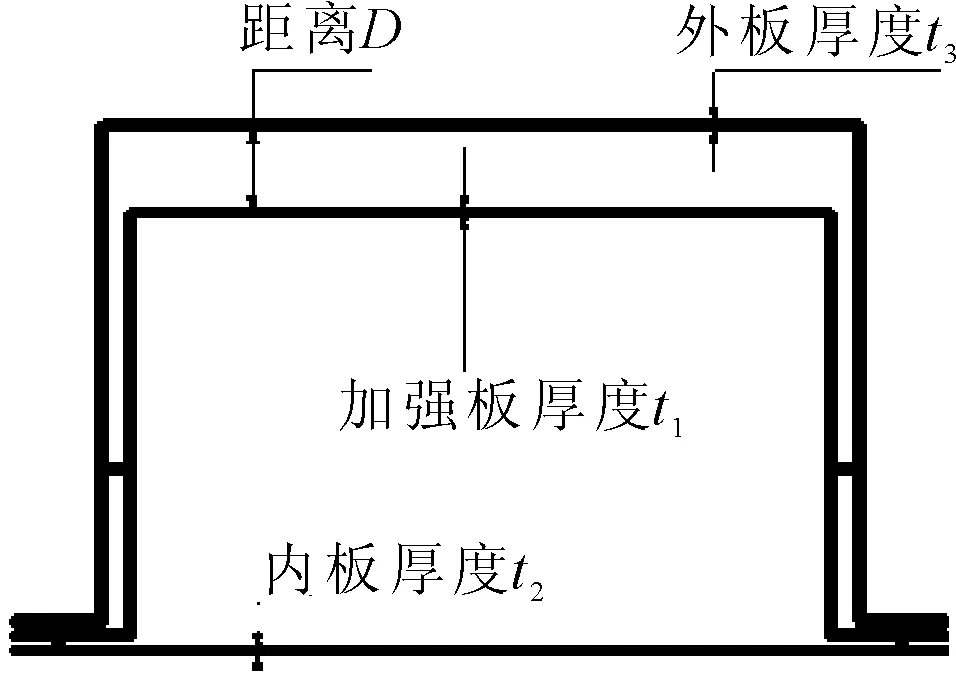
图1 带有加强板的单帽梁截面模型

选取的加工试件单帽梁结构见图2，具体俯视图见图2a)，横截面见图2b)，带有加强板的单帽梁总体长度为1 000 mm，外板宽130 mm，加强板宽125 mm,加强板到外板的距离为15 mm，内板宽160 mm，整体高度85 mm，内外板及加强板厚度均为1.5 mm；材料为B400-DP780.

图2 单帽梁截面结构

2 三点弯曲试验

2.1 抗弯性能指标

为了更好更方便的研究薄壁梁的抗弯性能，三点弯曲实验从主要以下两个指标进行评判：平均加载力Fmean及质量m.平均加载力Fmean表示的是加载力在整个压溃过程中的平均值，反映的是压溃过程的抗弯性能,见式(1).

(1)

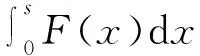
随着人们环保意识的提升，汽车油耗性能要求也愈发严格，轻量化也成为车身结构设计中的重要课题[5].在考虑到抗弯性能的同时，还需要结合轻量要求，因此，有必要将质量m作为评判标准之一.

2.2 三点弯曲试验的工况

在万能试验机上对试件进行准静态三点弯曲试验以观察试件的变形过程.试件采用两端套接的约束方式，这种在很大程度上模拟真实碰撞中B柱被约束的情况，同时保证试验的可靠性.其中试验压头高45 mm，前端半径15 mm，支撑座与试件接触处圆柱半径15 mm，两支撑架之间的跨距820 mm.支座及压头材料均为45#钢.试验开始前，加载速度设定为10 mm/min，压头加载行程为160 mm，最大加载力设置为25 kN，用以保证试验安全性.试验全程用摄像机记录压头与试件接触处变形情况.试验前装置见图3a).

图3 三点弯曲试验结果

试验过程中：初始阶段，塑性弯曲转角开始增大，在梁腹靠近受压一端出现膨胀点，此时塑性绞线还没有发生明显的滚动变形，随着塑性绞线滚动变形的显著发生，滚动变形出现干涉现象，并出现新的膨胀点，当转角增大到一定值，塑性绞线开始失效，最终试验完成后的试件结构见图3b)～3c)，在横向载荷作用下产生整体弯曲变形，压头与试件接触处产生较大塑性变形.试验全程焊点未失效，试件各处未发生撕裂断裂等失效现象.其中结构的塑性铰与褶皱承担主要吸能作用.

2.3 三点弯曲试验验证

三点弯曲试验后，将B柱试验件在试验中得到的加载力-位移曲线与简化后的带有加强板的单帽梁试验件的进行对比见图4.

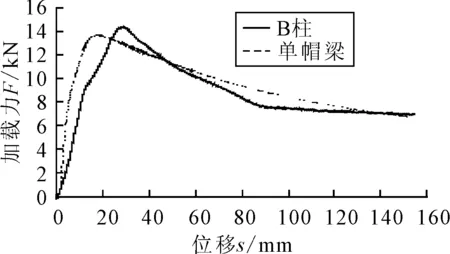
图4 B柱、单帽梁试验加载力-位移

B柱与单帽梁试验所得的加载力-位移曲线整体看来变化趋势趋于一致，只是到达加载力峰值的位移及加载力峰值有所不同，产生这样偏差的原因是因为样件在加工过程中存在加工误差及随机误差，同时简化后单帽梁也不能完全与B柱一样，所以产生这样的偏差.但都在可接受范围内，故在很大程度上简化后的单帽梁可代替B柱进行三点弯曲试验，所得结果可靠.

2.4 三点弯曲试验的仿真与对标

对试件、支座分别依据各自的尺寸用Hypermesh软件在LS-DYNA环境下建立有限元模型.有限元模型见图5，B400-DP780材料采用MAT24，密度为7.85 g/cm3，弹性模量为210 GPa，柏松比为0.3，材料屈服强度为422 MPa.

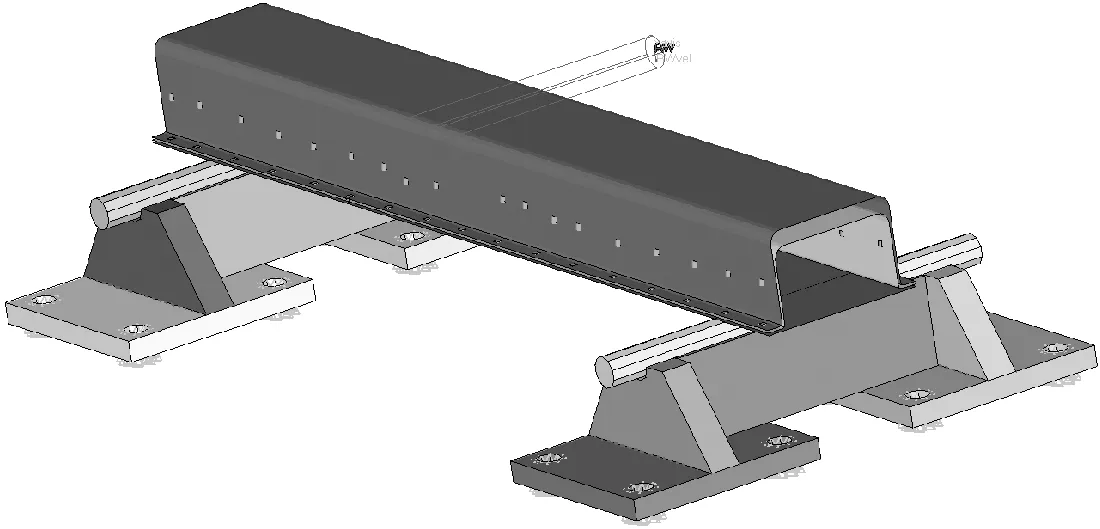
图5 准静态三点弯曲有限元模型

单帽型薄壁梁试件设置为5 mm的Belyschko-Tsay 壳单元，以四边形和三角形壳单元为主，四个支架底座的六个自由度完全约束.按试件实际焊点布置建立单帽梁外板与内板及外板与加强板的焊点单元,焊点单元类型取Mat100(hex)，接触类型为点面接触(node-to-surface)，各Component间建立自接触，接触类型为面面接触,避免单元间穿透.压头简化为半径为15 mm，长为300 mm的圆柱体刚性墙，速度设定为2 m/s，摩擦系数设置为0.2，总时长为85 ms.

将模型导出K文件提交给LS-DYNA求解器计算，仿真得到的加载力-位移曲线与试验加载力-位移曲线对比见图6，其变化趋势整体一致.仿真与试验结果误差均小于10%，处于可接受区内，因此仿真模型准确，其结果可行.

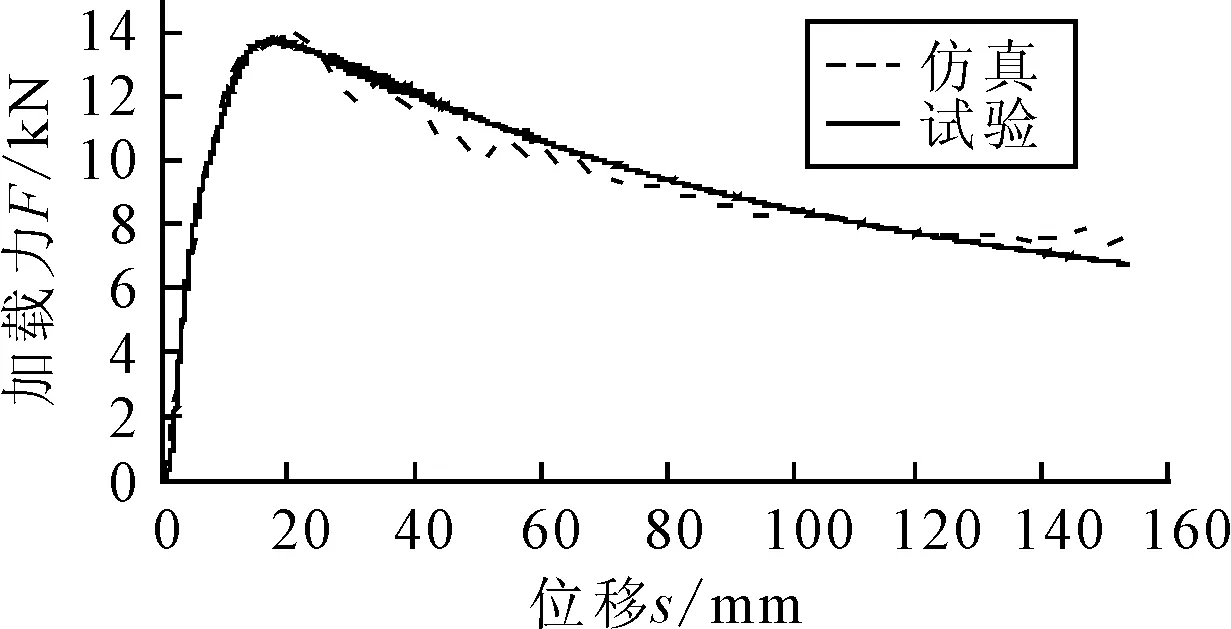
图6 试验仿真加载力-位移曲线对比

3 B柱结构的多目标优化

3.1 优化问题的定义

B柱优化问题属于耦合问题，设计目标相互影响，即导致一个目标向理想方向改变的同时另个目标朝较差方向改变，因此不存在绝对最优解.同时由于目标函数的连续性，也找不到所有的非劣解.但是可以根据输出的有限个非劣解解集构成Pareto前沿，为决策者寻找相对最优解提供指导.该多目标优化函数的数学模型为

(2)

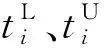
3.2 拉丁超立方抽样

拉丁超立方抽样是一种在约束条件下随机且均匀地生成样本点的试验设计.拉丁超立方仿真设计方法具有有效的空间填充能力和拟合非线性响应等优点[6].为了建立能够准确反映设计变量与目标函数关系的近似模型，本文选用拉丁超立方方法对由四个设计变量组成的样本空间进行采样，抽取30组样本点并根据样本点对仿真模型进行修改计算，得到每组样本点所对应的平均加载力Fmean及质量m.30组仿真设计抽样以及目标函数的部分值见表1.

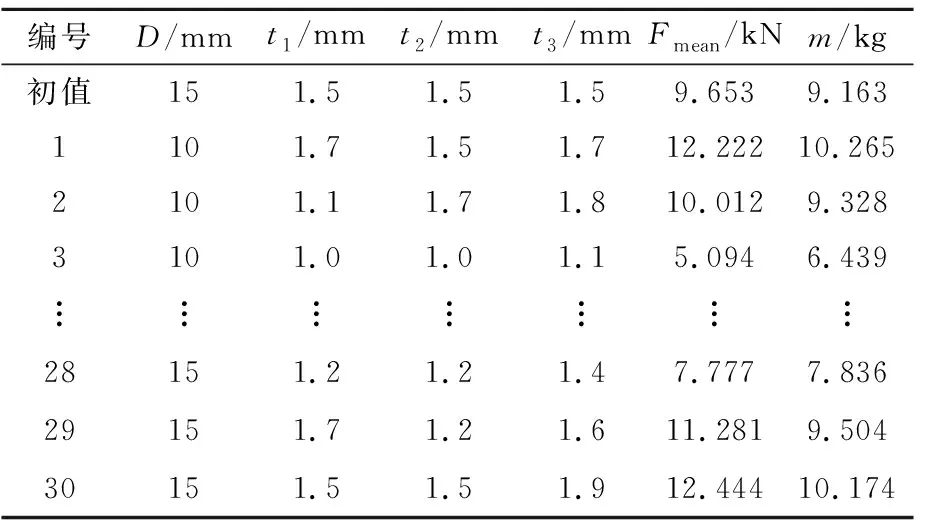
表1 拉丁超立方抽样及其目标函数值

3.3 响应面近似模型的建立

响应面方法目前已广泛应用于化工、农业和机械工程等领域[7].其基本思想是在试验测量、数值分析或经验公式的基础上，对整个空间内的样本点进行试验求值，从而构造目标函数和约束条件的全局逼近.在对接触—碰撞这样复杂的动力学问题进行抗撞性优化设计时，响应面法是一种快速、高效的近似求解方法[8].

根据30组样本点将单帽梁的四个参数作为输入变量，以平均加载力和质量为目标函数，分别建立二阶响应面近似模型.结果为

Fmean=-8.307+0.232D-4.358t1+4.691t2+

0.119t1t2+1.525t1t3-2.312t2t3

m=0.051+0.001D+2.511t1+1.230t2+

0.002t1t2+0.008t1t3-0.002t2t3

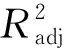
表2 响应面模型精度检验表

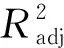
3.4 基于NSGA-Ⅱ算法的优化设计及结果分析

遗传算法作为一种模拟仿生学的进化算法，由于其良好的全局搜索能力被广泛应用于工程问题.然而，其过程复杂，且在高维问题中收敛速度很慢甚至难以收敛.由遗传算法发展而来的非支配排序遗传算法NSGA-Ⅱ是目前使用最多的多目标优化算法之一，具有解集的收敛性好、运行速度快及有效降低非劣排序遗传算法复杂性的优点，成为其他多目标优化算法的基准.

在多目标优化过程中，优化的目标是在平均加载力尽可能大的情况下使得质量达到最小.由于目标函数之间存在相互冲突，因此为了在非劣解集中找到一个相对最优解，需要对目标函数进行全面的评定.NSGA-Ⅱ遗传算法不需要决策者设置权重和比例系数，采用非支配解排序的遗传算法NSGA-Ⅱ对二阶响应面近似模型进行优化求解，在求解多目标优化最优解时，会自动计算出所有权重下的非劣解，这些非劣解所构成的解集是Pareto前沿.将遗传算法NSGA-Ⅱ中各参数设置为：种群规模48，进化代数500，其他设置为默认值.优化后，NSGA-Ⅱ算法迭代500次Pareto前沿见图7.

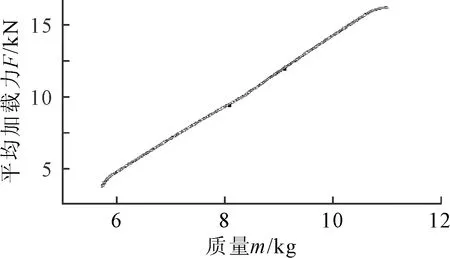
图7 NSGA-Ⅱ算法500次迭代的

Pareto前沿.

Pareto前沿产生后，试验者通过合理的选择标准选取某个非劣解作为优化结果.采用最小距离法计算在目标函数空间中每个非劣解到其他所有非劣解距离之和，其中距离之和最短的非劣解作为优化方案中一个相对最优解具体为

(3)

式中：D`为 相对最优解与其他非劣解之间的距离之和；m为目标函数的个数；fcn为第c组非劣解集的第n个目标函数值；min(fn(x))为第n个目标函数的最小值.

最终优化方案见表3，为优化后单帽梁各参数的预测值和仿真值.

由表3可知，优化后预测值中D为33.951 mm，t3为1.458 mm考虑到在仿真操作将数据进

表3 单帽梁优化结果 mm

行圆整，选用优化方案中非劣解的临近点作为最终优化值，即D为35 mm,t3为1.5 mm，其他值取优化后预测值结果.

3.5 单帽梁结果模拟验证

通过上述优化分析可知，对于本次优化，综合考虑抗弯性能及轻量化要求，所得到的最优方案为加强板厚度2 mm、内板厚度1 mm、外板厚度1.5 mm，加强板到外板的距离为35 mm.基于LS-DYNA进行有限元建模仿真计算，并利用后处理软件Hyperview对计算结果进行分析，优化后预测与仿真结果见表4.

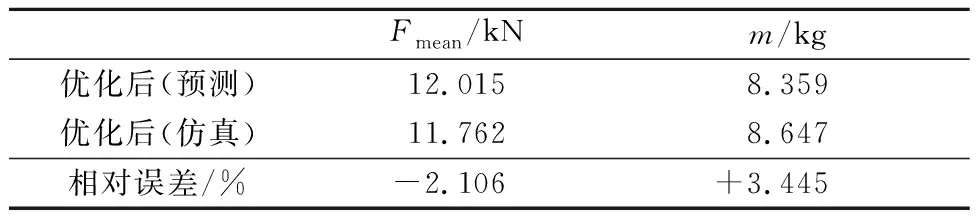
表4 优化后预测与仿真结果对比

由表4可知，将通过遗传算法NSGA-Ⅱ对响应面近似模型进行优化求解所得设计目标的预测值与基于LS-DYNA进行有限元建模仿真计算得设计目标的仿真值进行对比，平均加载力与质量的相对误差分别为2.150%,3.445%，均在以内，因此认为该优化方法可靠.优化前、后单帽梁模型仿真结果见表5，平均加载力提高了8.376%，质量比原来减少了5.631%.

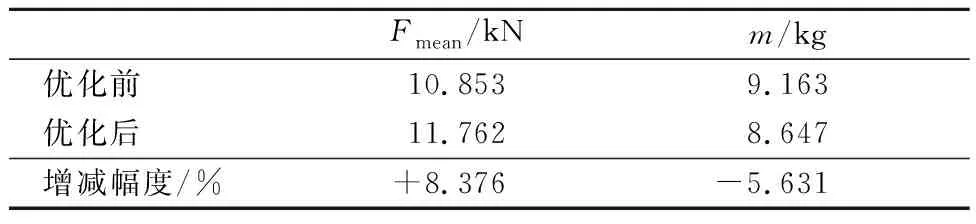
表5 优化前、后模型仿真结果

3.6 B柱结果模拟验证

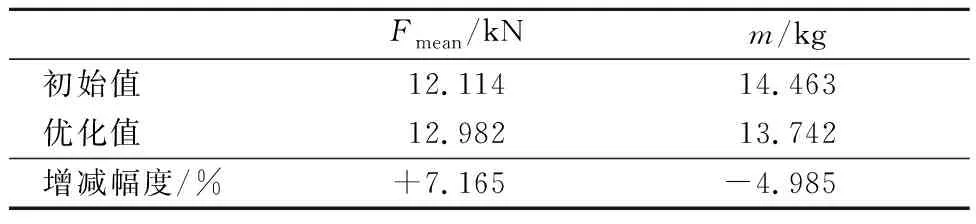
基于LS-DYNA对B柱进行有限元建模仿真计算，准静态三点弯曲工况下B柱模型见图8.将B柱仿真结果与原始B柱结果进行对比具体见表6.

图8 优化后B柱仿真模型

Fmean/kNm/kg初始值 12.11414.463优化值 12.98213.742增减幅度/%+7.165-4.985

由表6可知，B柱的平均加载力提高了7.165%，质量比原来减小了4.985%，提升侧面碰撞抗弯性能的同时也满足了轻量化的要求，达到本次优化的目的.

4 结 论

1) 根据B柱整体结构，将B柱简化为带有加强板的单帽梁，并将B柱与简化后单帽梁模型在三点弯曲工况下进行对比.

2) 将目标车型B柱简化为带有加强板的单帽梁后，采用拉丁超立方抽样对单帽梁的各板厚度、截面尺寸等参数进行设计采样，并通过二阶响应面近似模型建立近似函数与设计变量之间的关系，利用遗传算法NSGA-Ⅱ算出由非劣解集合成的Pareto前沿，从中找出满足条件的最优单帽梁的几何参数.结果表明，通过优化，使得平均加载力提高了7.165%，质量比原来减小了4.985%，在提升车辆侧面碰撞安全性的同时兼顾了车辆轻量化的要求.所提出的优化方案对提高车身侧围结构中B柱耐撞性能提供参考.