基于Canny的改进图像边缘检测算法

张月圆，曾庆化，刘建业，李一能，刘 昇

（1.南京航空航天大学导航研究中心，南京211106；2.中航工业洛阳电光设备研究所，洛阳471009）

0 引言

随着计算机科学的发展，图像处理技术近年来取得了丰硕的研究成果，在工业、军事、医学等领域得到了广泛应用［1］。边缘作为图像最基本的特征，能在保留物体形状信息的前提下，大大减少图像所要处理的信息。因此，边缘检测是图像处理领域最重要的关键技术之一，对于特征提取、描述及目标识别等后续研究都有着极大的影响。然而，由于图像边缘一般位于像素灰度值变化剧烈的位置，其与噪声信号一样具有高频特性，在检测中很容易产生伪边缘或漏检，不利于后续的提取和识别。所以，对图像边缘检测的研究具有非常重要的意义。

在众多图像边缘检测方法中，Canny算法由于其优良的边缘检测特性——高准确度和高信噪比，得到了广泛应用。但是，经典的Canny算法存在容易受噪声干扰且双阈值选取适应性不强的缺点，因而国内外的学者提出了很多改进方法。文献［2］主要通过调整邻域来降低噪声，但同时造成了弱边缘的漏检。文献［3］～文献［6］通过结合更多的图像信息来优化（如文献［3］基于多幅图像信息，文献［4］基于彩色图像色调信息，文献［5］基于局部图像块结构信息，文献［6］基于边缘长度和方向信息等），虽然这些改进方法增强了边缘的可靠性，但同时增加了计算负担。文献［7］针对特定图像——红外图像，研究了减少噪声的方案。文献［8］以非线性滤波器计算水平、垂直方向的梯度，区别噪声和边缘。文献［9］结合模糊神经网络和自适应中值滤波，实现了椒盐噪声干扰下的边缘检测。文献［10］结合优化模型，实现了一种生活场景中的边缘检测。文献［11］利用遗传算法，改进了阈值选取方法。文献［12］则基于遗传编码，实现了弱边缘的提取。虽然结合机器学习等算法，通过大量样本的训练，使检测器可以实现一个较好的效果，但该类方法对样本数量要求较高。

本文在分析经典Canny算法原理的基础上，针对其无法抵抗椒盐噪声干扰及双阈值选取问题进行了改进，提出了一种改进图像边缘检测方法。实验结果表明，该方法与经典Canny及其改进算法相比，有更好的抗噪性能和更好的检测效果。

1 经典Canny算法分析

Canny算法是一种基于图像梯度的边缘检测算法，其按照以下3个基本准则进行边缘检测：较高的信噪比、较高的定位精度和单边响应准则［13］。检测步骤如下：

1）使用Gauss滤波器对图像进行平滑处理，设原图像为I（x，y），则平滑后的图像H（x，y）可以表示为

2）基于平滑后的图像计算梯度幅值和方向，计算公式如下

3）根据梯度方向进行非极大值抑制。检测每一个像素点的梯度是否是周围具有相同梯度方向的像素点中最大的，是则保留，否则抑制。

4）双阈值判定边缘像素。该步骤需要设置高低两个阈值：TH和TL。 当边缘像素点的灰度梯度高于TH时，认为其是强边缘；低于TL时，认为其非边缘；介于两者之间时，若该点与强边缘相连，则认为其是边缘点。

与传统微分算子相比，Canny算子在被应用于检测图像边缘时具有运算速度快和检测精度高的优点，因而在实践中被广泛采用。然而该算法存在两个主要问题：在第一步中运用Gauss滤波器对图像进行平滑处理，虽然可以在一定程度上减少噪声影响，但很难滤除椒盐噪声的干扰；第三步中Canny算法的双阈值都是固定的，高低阈值依赖人工经验进行设置，目前还没有较好的判别高低阈值的理论方法。

2 改进边缘检测算法研究

针对上述分析，本文以Canny算法框架为基础，主要在以下两方面进行了改进：

1）采用改进AMF替代Gauss滤波对图像进行降噪处理；

2）结合Otsu和MEM提出改进双阈值选取方法，完成双阈值选取。

2.1 改进自适应中值滤波研究

椒盐噪声在图像上表现为同时产生高灰度噪声和低灰度噪声，具有比较高的随机性，一般采用非线性滤波方法来处理。在噪声密度较小的情况下，中值滤波即可去除椒盐噪声。为处理噪声密度较大的图像，文献［14］提出了AMF，即在中值滤波基础上，根据噪声密度调节滤波窗口的大小，其处理过程如下：

1）首先采用3×3的初始窗口Sxy进行计算，计算窗口Sxy中的灰度中值Zmed、最大值Zmax和最小值Zmin。

2）如果窗口Sxy中的灰度中值Zmed不在Zmax和Zmin之间，就自动增加窗口Sxy的大小，重复以上的过程直到设置的窗口最大值Smax或灰度中值Zmed在Zmax和Zmin之间。

3）依次用窗口Sxy中的每一点灰度值Zxy与灰度最大值Zmax和灰度最小值Zmin进行判断，如果介于其间，输出原值，反之输出Zmed。

分析步骤3可知，AMF一方面容易将极值点误判为噪声点并进行滤波处理；另一方面，在判断为噪声点后，以窗口内初始灰度中值替换输出也容易造成过度平滑，在滤波的同时损失图像细节，不利于后续的边缘提取。因而，本文在其基础上针对极值点进行判断，并将中值替换修改为窗口内除去极值点的均值替换，如式（4）、式（5）所示。

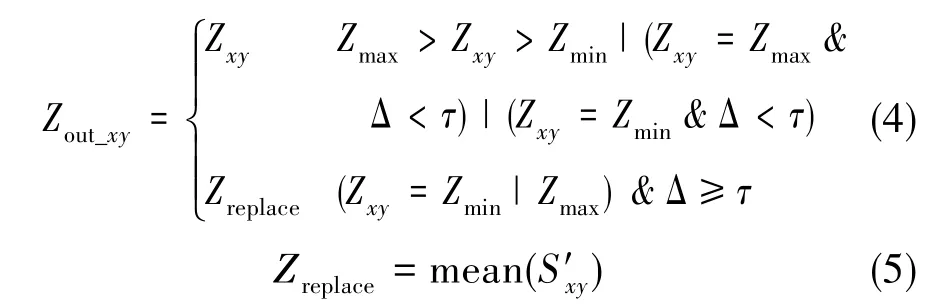
式（4）中，Δ=Zxy-Zmed，τ=k（Zmax-Zmin），k=0.5。 其含义是当像素灰度值Zxy等于极值时，只有同时满足其与灰度中值的差大于阈值τ时才认为其为噪声点，从而降低极值点被误判为噪声点的概率。τ中的k值可根据实际情况进行调整，一般设为0.5即可。式（5）中，S′xy为窗口内除去噪声点后的像素灰度值之和。其含义是若某点像素被判断为噪声点，则该点输出窗口内除去噪声点后的像素灰度平均值。

改进AMF通过极值点判断保留了大部分的非噪声极值点，通过噪声点输出值剔除噪声影响，避免了过度平滑，因而其可以在滤除椒盐噪声的基础上尽可能地保留图像中的细节信息。

2.2 改进双阈值选取方法研究

在双阈值选取这一步骤上，传统方法凭借人工经验选取高阈值，然后取其一半作为低阈值。此方法过度依赖经验，适应性不强。考虑到不同阈值选取算法的特点（如：Otsu侧重像素的分布密集程度，MEM侧重像素的分布均匀程度），本文综合两者特点，提出Otsu和MEM双阈值选取算法，从而能够较好地描述目标与背景的差异。

Otsu和MEM均为单阈值动态选取方法。Otsu以直方图为基础，将图像用阈值T分成背景和目标两类，并使这两类类间方差最大，即目标与背景分别像素密度最大［15］。MEM则基于信息熵的定义，求解阈值T使目标和背景两类的信息熵之和最大，即目标与背景分别均匀程度最佳［16］。

针对自适应的双阈值选取方法，前人进行了许多研究，其中双重Otsu算法的应用较广泛。该方法首先以Otsu在图像区域求解最佳阈值，并将其作为高阈值TH，然后在0～TH之间再利用Otsu求解最佳阈值作为低阈值TL。 作者在针对背景较复杂的图像目标轮廓提取的实际研究中发现，用Otsu算法获得的高阈值容易引入更多干扰边缘，因此需要改进高阈值的获取手段。结合MEM算法侧重均匀性的特点，提出将MEM算法在图像区域内获取的最佳阈值作为高阈值TH，然后在灰度梯度幅值0～TH之间的图像范围内求取Otsu最佳阈值作为低阈值TL。 具体求解过程如下。

一幅大小为M×N、灰度级为L的图像，设图像中灰度级为i的像素个数为Ni，则灰度级i的概率为

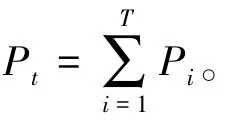
根据MEM的思想，高阈值TH的求解公式为

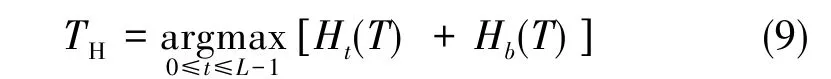
在灰度梯度幅值0～TH之间的图像范围内，运用式（10）求解低阈值TL

3 实验测试

为了评估本文所提出的改进算法的检测效果，本文在vs2010配合OpenCV2.4.9的实验环境下完成了测试。

3.1 改进AMF实验测试

为了客观评价滤波算法的降噪效果，本文以均方误差（Mean Square Error，MSE）和峰值信噪比（Peak Signal⁃to⁃Noise Ratio，PSNR）2 项指标评价滤波算法的降噪性能。MSE和PSNR的计算公式如下

式中，m×n表示图像大小，I′（x，y）表示原无噪声图像，IQ（x，y）表示降噪后的图像，R表示图像的灰度量级。

图1为Gauss滤波、中值滤波、AMF和改进AMF 4种滤波算法对不同噪声密度图像处理后的MSE和PSNR统计曲线，分别对降噪情况和失真情况进行了直观的展示。MSE越小表明降噪效果越好，PSNR越高说明图像失真越小。从图1可知，Gauss滤波难以滤除椒盐噪声，中值滤波和AMF可以滤除椒盐噪声，但同时损失了较多图像细节。本文改进的AMF，不仅在高密度噪声情况下可以取得略优于AMF的滤波效果，同时在低密度噪声情况下的降噪效果和图像抗失真情况均显著优于AMF。因而在将其应用于图像边缘检测算法时，既可以提高算法抗椒盐噪声干扰的能力，又能尽可能地保留图像细节。

图1 各滤波算法在不同噪声密度情况下的降噪效果和失真情况对比Fig.1 Comparison of noise reduction and distortion of each filtering algorithm under different noise densities

3.2 改进双阈值选取方法实验测试

为了验证改进双阈值选取方法的有效性，本文将其与经典Canny算法及双重Otsu改进方法进行了对比，如图2所示。

图2 双阈值选取方法对比Fig.2 Comparison of dual threshold selection methods

从图2可知，此类图像背景复杂且占据较大比例。经典Canny算法的双阈值选取为经验选择，使背景中的大量边缘被视为强边缘，从而干扰了目标边缘的提取。双重Otsu选取的高阈值偏低，使得边缘检测结果较Canny算法而言更为杂乱。本文提出的双阈值选取方法既保留了目标边缘细节，又减少了背景边缘的干扰，因而适用性更好。

3.3 改进图像边缘检测算法实验测试

为了综合评价本文提出算法的抗噪性能和边缘检测效果，本文将其与经典Canny算法及结合中值滤波、自适应中值滤波进行改进的改进Canny算法进行了对比。本文以准确度（accuracy）指标进行评价［6］，如式（13）所示。

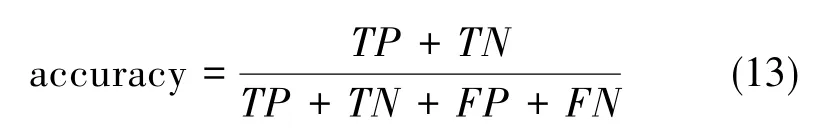
式中，TP为正确检测轮廓像素数，TN为正确检测非轮廓像素数，FP为错误检测轮廓像素数，FN为错误检测非轮廓像素数。

图3所示为2组实验的测试结果。每组图像从左到右依次为实验原图（含10%椒盐噪声）、作为基准的人工标注边缘（Label）、经典Canny算法进行边缘检测的结果、结合中值滤波改进的Canny算法（MC）进行边缘检测的结果、结合自适应中值滤波改进的Canny算法（AMFC）进行边缘检测的结果，以及本文算法进行边缘检测的结果。可以看出，经典Canny算法在含椒盐噪声的情况下基本失效，结合中值滤波和自适应中值滤波的改进算法虽然在一定程度上克服了椒盐噪声干扰，但边缘检测准确度均低于本文算法，如表1所示。MC由于中值滤波降噪效果较差，在检测结果中保留了部分噪声形成的边缘。AMFC可以较好地抗椒盐噪声干扰，但由于双阈值选取不合适，因而保留了很多背景杂乱的边缘。本文以改进AMF替代Gauss滤波对图像降噪，从而增强了边缘检测算法的抗噪能力，以改进双阈值选取方法设置高低阈值，使边缘检测结果去除了背景干扰，保留了大部分主体目标轮廓，准确度达到96%以上。相比其他算法而言，本文算法最优。

图3 本文算法与经典Canny算法及其改进算法对比Fig.3 Comparison of the algorithm proposed with Canny and its improved algorithm

表1 本文算法与Canny算法及其改进算法边缘检测的准确度统计Table 1 Accuracy value of proposed algorithm and Canny and its improved algorithm for edge detection

4 结论

本文在分析经典Canny算法原理及其不足之处的基础上，针对其无法抵抗椒盐噪声干扰和双阈值选取适应性差的问题进行了改进。首先利用改进AMF替代Gauss滤波，使改进算法在尽量保留图像细节的同时可以较好地抗椒盐噪声干扰。然后在研究Otsu和MEM的基础上，提出了本文改进双阈值选取方法，该方法可以较好地适应背景复杂的图像，以人工标注边缘为基准，边缘检测准确度可以达到96%以上。综合实验结果表明，本文算法与经典Canny算法及结合中值滤波、AMF的改进Canny算法相比，可以较好地抗椒盐噪声干扰并且在背景复杂的图像中达到更好的检测效果。

但是由于光照、拍摄角度等问题，图像往往存在边缘断裂现象，即一个独立物体的边缘并不闭合，边缘可能由多段细小边缘组成。后续研究可以进一步结合边缘修复连接完善边缘检测效果，使边缘检测可以结合具体的应用目标得到更好的检测效果。