基于栈式稀疏自编码器的青光眼眼底图像识别研究∗

曹桂铭 丁香乾 高政绪

（中国海洋大学 青岛 266100）

1 引言

青光眼是眼科一种常见的疑难病，症状为眼压升高使得眼部功能发生障碍，并伴有瞳孔发青绿色这一视网膜形态的变化［1］。其具有危害大，高隐蔽性，发病率高等特点。青光眼严重危害患者的身体健康，眼内压力长时间过高，会损害视神经，患者就会出现视力逐渐减退或失明［2］。同时由于其发病初期很难被发现，一旦出现视力下滑，则进入了晚期，已经造成不可恢复的损伤［3］。据统计，全球人群中，青光眼的患病率为3.54%，约有6426万人；预计到2020年和2040年分别将达7602万人和11182万人［4］。

尽管青光眼严重威胁着我们的身心健康，但目前对于青光眼疾病的研究还处于初级阶段，远远不能满足人们的需求。因此对青光眼的研究是很有必要的，只有对其早诊断早治疗才能减少它对视力的损害。眼底图像是青光眼判别的最重要标准，由于眼底图像的复杂性高，因此在实际操作中有很大的困难［5］。相关研究者取得了一定的成就：干能强［6］提出了基于主成分分析法（PCA）的青光眼识别方法；黄元康［7］提出一种基于图像分割的马尔科夫随即场青光眼眼底图像识别技术；德国研究者研制了一种Zeiss青光眼诊断分析仪，具有方便快捷的特点，但是识别精度不高。

本文提出了一种基于栈式稀疏自编码器的青光眼眼底图像特征提取及图像识别模型。只需将眼底图像做简单的预处理即可作为模型的输入，相比于需要进行眼底图像分割的方法更为简单。采用逐层贪婪训练法从无标签的数据集中学习到数据的内部特征，将学习到的特征作为Softmax分类器的输入进行分类，判断是否患有青光眼。并通过仿真实验，证明了该方法是有效可行的。

2 算法描述

2.1 栈式自编码神经网络

自编码器（Auto-encoder）是一种尽可能使输出数据等于输入数据的无监督学习的神经网络［8］，是一个只有一个隐含层的单层自编码器，如图1所示。单层自编码器包括一个输入层，一个隐含层和一个输出层，其中+1是偏置项系数。）

图1 单层自编码器

自编码器的训练分为编码和解码两个过程。编码过程是使输入数据x通过线性运算以及激活函数，再映射到隐含层得到编码结果的过程［9］，有

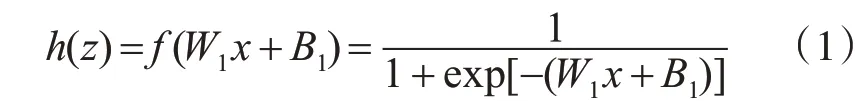
其中f(z)=1∕[1 +exp(-z)]是激活函数，h（x）是隐含层神经元的激活值，W1是权值矩阵，B1是偏置值矩阵。

解码阶段是将编码阶段得到的数据特征表达，即隐含层的输出，作为输出层的输入，对其进行重构，得到与原始数据尽可能相等的输出。

栈式自编码器是将多个稀疏自编码器堆叠而成。栈式自编码器可以逐层提取数据的特征。将栈式自编码器的输出作为Softmax分类器的输入，即是本文所采用的模型［10］。其结构如图2所示。

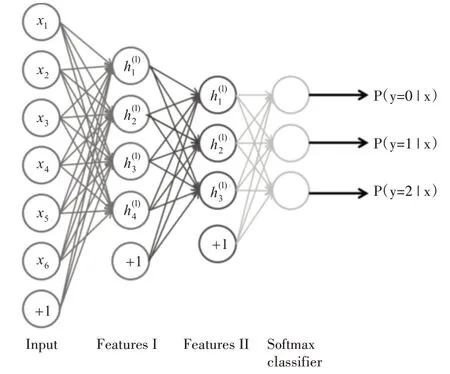
图2 栈式自编码器网络结构

具体来说，首先进行此分类器的逐层预训练。利用不带标签的数据样本通过逐层贪婪训练法，最小化重构误∑s[xi-h(xi)]2，训练第一层隐含层L2，i=1得到其参数W1，B1。这样就用一组基的线性组合来表示了输入数据。再将这一组向量作为第二层隐含层L3的输入，对L3进行训练，得到参数W2，B2。在逐层训练每一层的时候，其他各层的参数保持不变。在预训练完成后，通过反向传播算法对所有层的参数进行微调，使分类结果更加准确。如果在预训练的过程中就对参数进行微调，可以使参数达到局部最优，但不会达到全局最优［11］。

假设wlji代表神经网络中第l层第j个神经元和第l+1层第i个神经元之间的权重系数，bil代表神经网络中第l+1层的第i个神经元的偏置项，zil+1表示第l+1层第i个神经元所有输入神经元的加权和，sl代表神经网络中第l层中神经元的总个数，则有

定义神经元的激活函数为f(z)，h(il)表示第l层神经元i的激活值，则有：h(il)=f(zi(l))。

用m表示输入样本个数，x表示输入，y表示输出（x=y），λ表示权值衰减系数，本文所定义的代价函数为［12］

其中，第一项为误差平方和项；第二项为规则化项，是为了减小权值，防止过度拟合。

2.2 栈式稀疏自编码神经网络

研究表明，人的大脑在感应外界刺激时，只有一部分神经元处于活跃状态，因此稀疏的表达更符合我们人类的神经系统。本文假设神经元的激活函数是Sigmoid函数。稀疏性可以被简单地理解为：当神经元的输出接近于1时，则它被激活，而输出接近于0时，其被抑制。因此使神经元大部分被抑制的限制条件称为稀疏性限制［13］。

用a(j2)(x)表示在输入为x的情况下，隐藏神经元j的激活度。并把隐藏神经元j的平均活跃度表示为。在此，稀疏性限制可以表示为ρˆj=ρ，其中ρ是稀疏性参数。ρ通常是一个接近于0的较小的值。为实现稀疏性限制，在原来的损失函数中加入一项惩罚因子。使用相对熵作为惩罚因子，可表示为

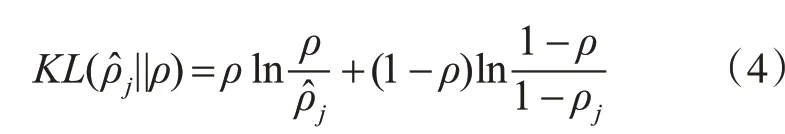
因此栈式稀疏自编码器的损失函数为

在根据损失函数进行微调的过程中，为了计算公式中KL(ρˆj||ρ)的导数，通常采用迭代的方法，像梯度下降发。根据BP算法，从后一层到前一层反向计算误差项，每一层的误差项为

根据公式，需要知道平均激活度ρˆj的计算，因此先需要对所有训练样本进行一次向前的传播计算，得到平均激活度ρˆj。此神经网络最终的偏导数计算为

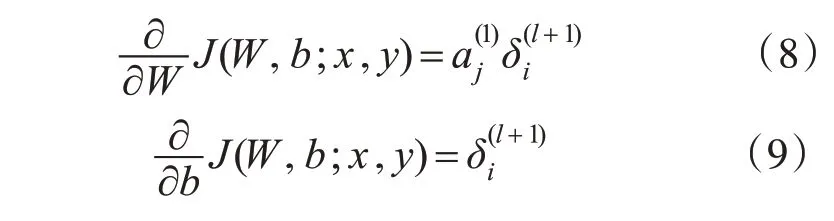
通常式（8）、（9）用矩阵矢量符号重写，该神经网络的权值项和偏置项的梯度下降方法为［14］：

2.3 Softmax回归

本文采用Softmax分类器对学习到的特征进行分类。Softmax模型如下：

其代价采用最大熵模型，代价函数为

其中k表示类别数目，1｛y（i）=j｝为示性函数。为了避免过拟合，在代价函数中加入正则化项，新的代价函数为凸函数，存在唯一的极小值，因此可以保证得到唯一的最优解，最终的代价函数为［15］

3 仿真实验结果

3.1 实验数据

实验数据采用来自某医院提供的青光眼患者和正常人的眼底图像共10000幅，其中青光眼眼底图像为5500幅，正常的眼底图像为4500幅，将图像样本分为3个子数据集。样本具体信息如表1所示。

表1 数据集

其中无标签训练集用于网络模型的特征学习，学习眼底图像的特征。有标签训练集用于最终分类器的训练。有标签测试集用于测试模型分类的准确性。

3.2 眼底图像处理

将原始眼底图像进行归一化，转化为灰度图，图像增强和去噪处理，转化为150×150的灰度图像，如图3所示。

图3 眼底预处理

3.3 建立分类模型

由于目前对于栈式自编码器构建过程中参数的确定并没有足够的理论方法，因此本文通过反复对数据集进行实验来确定。最终确定的几个主要的参数：稀疏参数ρ取0.005。学习速率为0.01，精神元激活函数为Sigmoid，迭代次数200次。本文采用Matlab R2014a作为编码工具，设定网络结构为150×150-10000-2500-500-100-1。最后一层使用Softmax回归对样本进行分类。

将预处理后的眼底图像输入稀疏自编码器。采用逐层贪婪训练法从无标签的数据集中学习到数据的内部特征，将学习到的特征作为Softmax分类器的输入。然后利用带标签的数据通过反向传播算法对稀疏自编码器进行调优。

3.4 对比分析

本文使用眼底图像测试集数据对神经网络模型的分类精确度进行测试，并与传统PCA和BP神经网络方法进行比较，测试结果如表2所示。

表2 测试结果

由表2可以发现，在对1000个测试集样本进行处理过程中，稀疏自编码器模型特征提取的准确率最高。相对于其它方法，本文提出的稀疏自编码器模型能够明显的提高特征提取能力，进而提高识别的准确率。

4 结语

因此本文提出了一种基于栈式稀疏自编码器的青光眼眼底图像识别模型。只需将眼底图像做简单的预处理即可作为模型的输入，无需对图像进行分割。采用逐层贪婪训练法从无标签的数据集中学习到数据的内部特征，将学习到的特征作为Softmax分类器的输入。然后利用带标签的数据通过反向传播算法对稀疏自编码器进行调优。最后使用测试集数据对整个模型进行测试。本文以正常的眼底图像和青光眼眼底图像为实验对象，并与PCA，BP方法进行实验对比。结果表明，本文提出的稀疏自编码器模型提取眼底图像特征的能力更好，识别准确率高于其他两种方法，对青光眼的识别具有一定的实用价值。