构造图形解中国古算题

王凯成

我国古代数学专著《孙子算经》《九章算术》《算法统宗》等收录了大量有趣的数学题，其中《孙子算经》“鸡兔同笼”一题被编排进小学数学新教材中。這一做法是对我国数学文化的传承与发扬。本文对入选小学数学教材的一些古算题利用长方形图解答，帮助老师们拓宽解题思路。

例1今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？（见《孙子算经》，人教版小学数学教材六年级上册）

解：依题意，可以画两个长方形图（如图1、图2）。

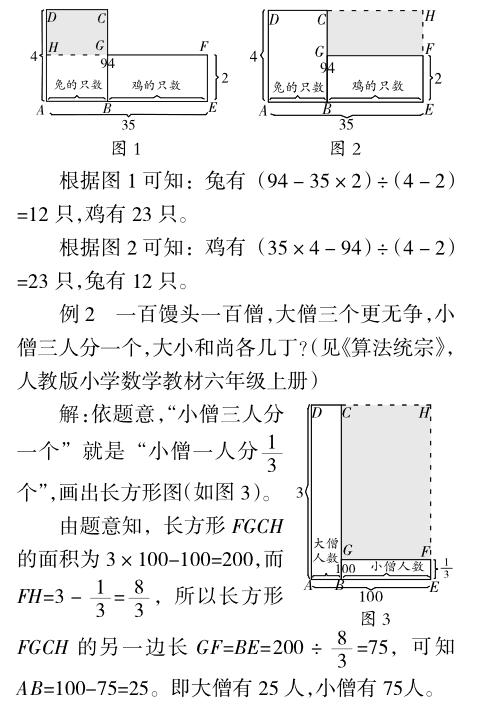
例3假如井不知深，先将绳三折入井，绳长四尺，后将绳四折入井，亦长一尺，问井深及绳长各若干。（见《算法统宗》）

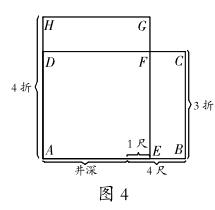
解：依题意画出长方形图（如图4）。

由于长方形ABCD与长方形AEGH的面积都表示绳的总长度，所以长方形ABCD与长方形AEGH的面积相等。长方形ABCD与长方形AEGH的面积都减去长方形AEFD的面积，可知长方形BCFE与长方形FGHD的面积相等。而长方形BCFE的面积为（4-1）×3=9，即知长方形FGHD的面积是9，而长方形FGHD的一条边DH=4-3=1，所以另一条边DF=9÷1=9。即知：井深9-1=8（尺），绳长为9×4=36（尺）或（9+4-1）×3=36（尺）。

用绳测量井深，《孙子算经》和小学数学新教材中都有类似的问题。

《孙子算经》中的题：今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺。问木长几何。（屈绳指把绳对折）

数学教材中的题：用绳子测井深，把绳三折来量，井外余16分米；把绳四折来量，井外余4分米。求井深和绳长。

中国古代算术题无论是内容（紧密结合当时的生产和生活实际）还是形式（大多以诗词形式）上都具有趣味性，容易引起学生的学习兴趣。通过解答适合小学生的中国古代算术题，学生体会到数学能够解决人类的现实问题，数学非常有用，感受到解决人类的现实问题促进了数学的发展。

（作者单位：陕西省小学教师培训中心）