二阶斯托克斯非线性潮波对潮汐贯流式水轮机性能的影响

冯建军，朱国俊，王 准，吴广宽，罗兴锜



二阶斯托克斯非线性潮波对潮汐贯流式水轮机性能的影响

冯建军，朱国俊※，王 准，吴广宽，罗兴锜

（西安理工大学水利水电学院，西安 710048）

双向贯流式水轮机在潮汐能开发中的应用广泛。在海洋波流条件影响下，潮汐能机组在反向运行过程中的水动力性能变化是潮汐能机组研发过程中需要考虑的重要问题。该文采用二阶斯托克斯非线性潮波对海洋潮波来流进行了模拟，建立了二阶斯托克斯非线性潮波边界下的潮汐贯流式水轮机性能分析模型并验证了模型的可靠性。以该模型为基础，采用CFD方法，对某一潮汐贯流式水轮机在反向运行时的内部流动进行数值仿真，重点研究了动态波流边界对贯流式水轮机反向运行时水力特性的影响。研究结果表明：1）考虑波流耦合作用时，潮波与坝体发生碰撞后损失了大部的动能，形成的反射波流，覆盖下一个波峰前的气体形成大气泡进入海洋内部；2）来流潮波与坝体壁面反射潮波的相互作用是形成潮汐贯流式水轮机取水口处夹气涡的原因，形成的夹气涡在液面下旋转前进流入内流场黏附于流道上侧，压缩流场过流面积，形成了一个低压低速的夹气涡流动带，从而改变内流场流动分布和贯流机组的特性；3）动态波流的作用使得潮汐贯流式水轮机转轮叶片上的受力呈现较大幅度波动，叶片受力的低频幅值会随着夹气涡的发展而逐渐增大。同时，在波流影响下机组出力的波动幅度达到3.86%，远高于无波流作用下的不足1%，从而导致电能质量下降。

水轮机；模型；计算机模拟；波流耦合作用；水力性能；夹气涡

0 引 言

潮汐能量是一种无污染、蕴含量巨大的海洋能，它泛指海水涨潮和落潮时形成的水的势能。不同的地区常有不同的潮汐系统，它们都是从深海潮波获取能量，尽管潮汐很复杂，但任何地方的潮汐都具有其特殊的规律性，可以进行准确预报，人们利用潮汐能的这种特征建造了潮汐能电站。由于潮汐能电站具有运行区水头极低、水头变动速度较快、过流湍急和受到潮波影响等因素，贯流式机组流道相对平直，避免由于流道弯折等结构原因而形成的水流流速分布不均匀，使得机组整体拥有较高的效率[1]。同时贯流式机组在极低水头工况下也能较为稳定的运行，低水头运行范围内也拥有较宽的运行区域[2]。综合此类特性，贯流式水轮机在浅海波流作用影响下的工作情况及其相应表现出的水动力性能也就成为海洋能转换的研究和探讨的重点对象。

海面潮波现象来源于潮汐作用，是海水表面发生的一种在竖直方向的波动现象，以类正弦波或类余弦波的形式出现，带有能量传递；潮流是海水的水平流动形式，这种此起彼落的海水运动，称为波流运动。由于海洋陆地热力性质差异和天体运动、大气循环、水循环等复杂地理因素，潮波总是普遍存在于流动水体的增水侧方向。处于过渡水深的潮汐能发电站一般采用贯流式水轮机，前人已经对该型机组做出了大量的分析研究。钱忠东等[3-4]进行了灯泡贯流式水轮机的全流道压力脉动数值模拟研究，得到了在非自由水面的稳定流动条件下贯流式机组的压力脉动特性；刘延泽等[5-6]探究了考虑重力因素后，评估了灯泡贯流式水轮机流场特性及水力性能等相关问题；王正伟等[7]分析了无波条件的双向灯泡贯流式水轮机在流道内造成水力损失的原因，并且对这种水力损失产生的影响进行了总结；赵亚萍[8]对低水头贯流式水轮机在考虑重力条件下含自由液面流场与不含自由液面流场的水力特性差异进行了分析和总结，分析了贯流机组桨叶在这种流场内的转动过程会出现受力波动，还有Soohwang等[9-10]也对自由液面下的贯流式机组内流特性开展了研究。前人研究成果十分丰硕，但是，大都忽略了工作流场中因水体动态效果对机组造成的水力特性改变，对于潮汐能贯流式水轮机组而言，自然海况中的海洋潮波动态变化是普遍存在的，工作过程中叶片上的载荷也因此呈非对称非稳态变化，同时，加入重力因素后，流场竖直方向的受力和流动情况必然分布不均[11-13]，过流管道内的贯流机工作条件会受反向工况下潮汐波流影响，功率会变得不稳定，也即这种动态的海流条件不稳定波动必然会影响潮汐能贯流式水轮机组工作时的水力特性[14-15]。因此有必要开展动态波流作用下的贯流式机组内部流动特性分析为潮汐贯流式水轮机的水力设计及运行提供指导[16]。

本文以某单库双向型潮汐电站的贯流式水轮机为分析对象，建立了反向发电时动态潮波边界条件下的贯流式水轮机内部流场数值计算模型[17]，并基于该模型获得了反向发电运行时贯流式水轮机在动态波流水面影响下的机组能量特性、转轮叶片力特性以及尾水管的压力脉动特性[18-19]，阐明了反向发电条件下海洋潮波作用对贯流式水轮机水力性能的影响机理，为自然海况条件下运行的双向潮汐贯流式水轮机的水力设计及运行提供有价值的理论依据。

1 可靠性验证及数值计算模型的建立

1.1 几何模型及计算域网格划分

本文所研究的对象是用于潮汐能发电的某双向贯流式水轮机原型机，机组转轮直径为2.5 m。转轮叶片数为4个，导叶高度0.345 4 m，轮毂比为0.38，导叶数为16，额定转速125 r/min。双向贯流式水轮机在反向发电运行时，入口侧为海洋潮波来流，出口侧为峡湾水库区；正向发电时，入口侧为峡湾水库区，出口侧为海洋。正向工况为从峡湾到海洋方向，湾内空间较小，几乎没有水面波动现象，所以在本研究中可以将其水位近似认为是恒定值；反向工况为海洋流向峡湾水库方向，海洋潮汐波流的起伏现象明显，在反向工况的波流具有复杂的形成原因和运动方式，海水自由液面持续发生的波动现象，波长较长，带有能量的传递[20-21]。根据反向发电条件下的机组运行原理，本文建立了动态潮波影响下的贯流式水轮机内部流动分析计算域，来研究海洋域动态波流涌浪对潮汐能贯流式机组运行的影响。同时为了简化计算模型，忽略坝后无波流现象的水库域，使计算所耗时长大大降低。根据上述原则建立考虑动态潮波边界条件下的贯流式水轮机流场分析计算域如图1所示。为了兼顾整体计算域的网格经济性，海洋域的长度取为了潮波波长的5倍，宽度取为了进水口宽度的2倍，高度取为平均水深和0.5倍波高之和的1.8倍。

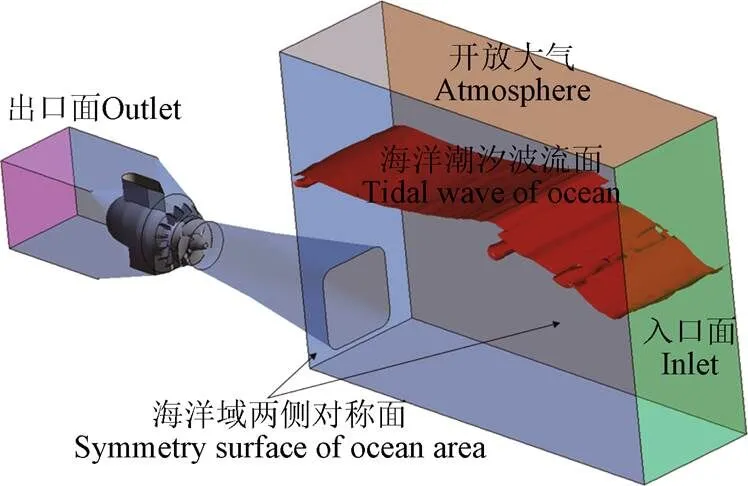
图1 海洋域边界设置

对计算域整体采用块结构化网格进行离散，网格如图2所示。

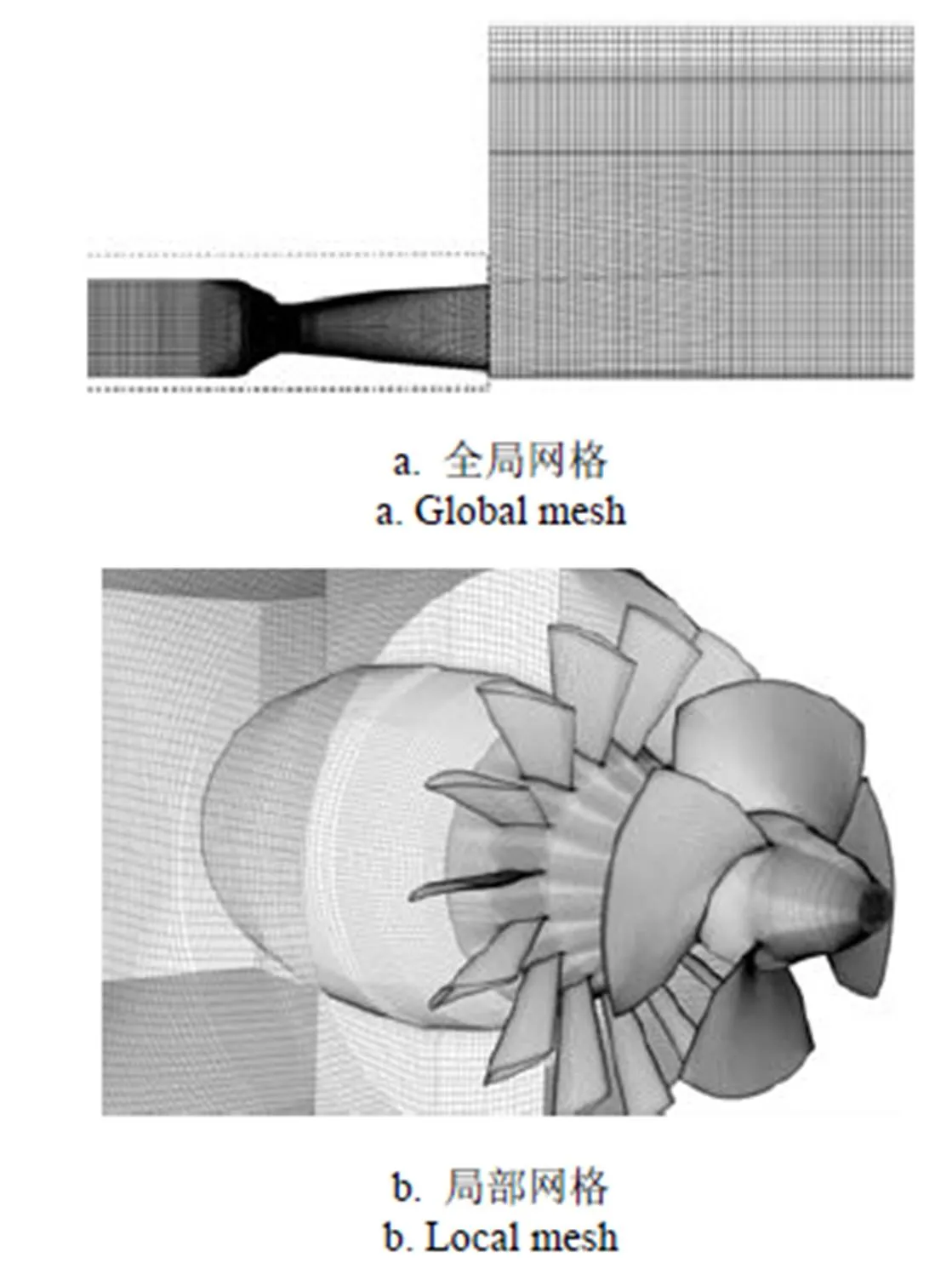
图2 水轮机计算域网格

网格数量既对数值分析的结果有重要的影响，又决定了计算所占用的资源和时间。水力效率为水轮机最重要的技术指标之一，其定义如式（1）所示。

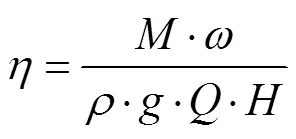
式中为转轮的扭矩，N·m；为旋转角速度，rad/s；为流量，m3/s；为工作水头，m；为水流密度，kg/m3；为重力加速度，m2/s。

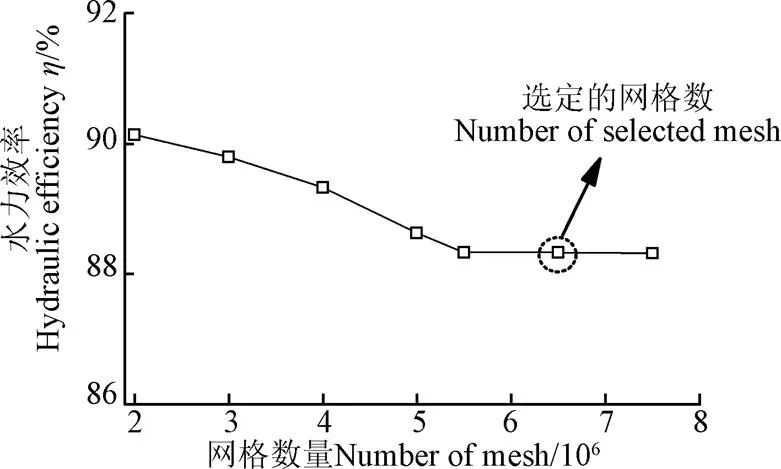
图3 网格无关性验证

为了对网格数进行无关性验证，本文以水轮机正向发电时最优工况的水力效率为判断依据对计算网格进行无关性验证，验证计算时海洋域给定为静止水面。如图3所示，随着网格数量的增大，贯流机的水力效率愈趋于平稳。最终选取网格数为652万，来进行进一步的数值研究。此外，以上网格能保证在水轮机内各个近壁区的无量纲壁面距离+小于100，结合可根据比率缩放的壁面函数，能适应所选的RNG湍流模型[22-24]。

1.2 计算方法可靠性验证

对该贯流式水轮机的缩比模型进行了模型试验，模型转轮直径1m=0.35 m，试验装置如图4所示。在模型试验中，采用Rosemount公司生产的8700系列电磁流量计来测量流量，误差为±0.17%；采用Rosemount公司生产的3051系列差压变送器来测量水头，误差为±0.05%；通过安装在主轴上的德国HBM T12型扭矩仪测得力矩，误差为±0.12%；转速则由测功机主轴上安装的日本MP-981型转速传感器测得，误差为±0.06%。试验台对效率的综合误差小于±0.25%。在测得模型机的效率值之后，需根据国际通用IEC-60193标准[25]换算到原型1=2.5 m条件下，从而得到原型机的效率。

图4 贯流式水轮机模型试验装置

图5给出的是水轮机正向发电时机组水力效率计算值和试验值的对比，图中正向发电时的水力效率并未考虑潮波作用。由图5可知，数值计算值与试验值的变化规律吻合，数值计算值略高于试验值。计算值整体偏高的原因是数值模拟的过程中没有考虑叶片与轮毂、轮缘间的间隙泄漏损失。计算值与试验值的最大偏差发生在小流量工况，最大偏差值为2.2%，其余工况的偏差均小于2%，数值计算结果准确可靠，表明所采用的数值计算方法对潮波作用下的水轮机内流特性分析模型是可靠有效的，可用于开展后续研究工作。

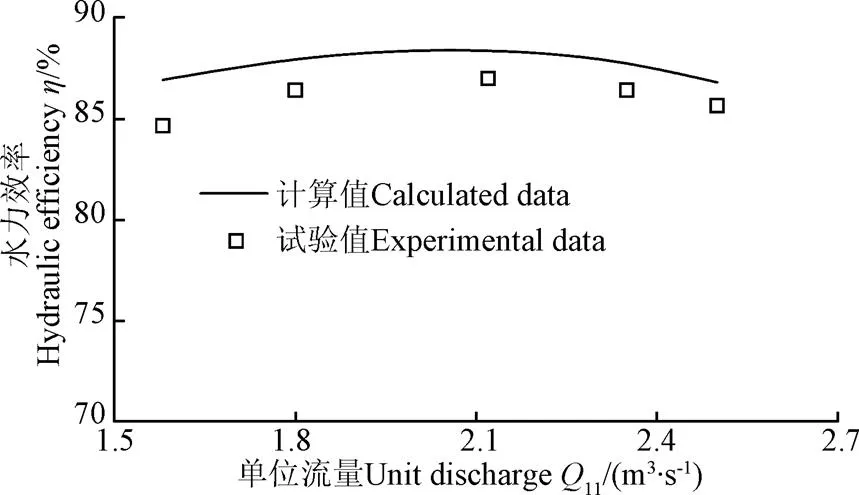
图5 计算可靠性验证

1.3 计算边界条件的设置

当波浪进行传播时，会逐渐形成波峰波谷明显、波形规则的规则波，因此可以采用二维平面波的数学模型来描述其运动。为了更好地模拟来流方向的海洋涌浪海波流动情况，将波流在潮汐能电站近岸区域的振幅视为相对于其波长而言的相对小量，将非线性的水面边界条件简化，以图2所示的计算域为基础建立了潮波作用下的水轮机内流特性分析模型，该模型通过在海洋域进口设置潮波速度边界条件实现潮波流动的数值模拟。潮汐能水轮机海洋侧进水口处的波浪运动的波高波长在正常的海况下都是有限值，因此根据波浪力学理论可以采用有限振幅波描述此处的波浪运动。其中，二阶斯托克斯非线性潮波是应用最为广泛的一种非线性有限振幅波浪理论模型，它的波面不是简单的余弦或正弦曲线，而是波峰较陡、波谷较坦的非对称曲线，相比于正弦波或者余弦波模拟的潮波流动，二阶斯托克斯非线性潮波运动的特征更加适用于描述近海受海底影响的非线性潮波运动，而潮汐电站的地址通常位于海湾、江河口处[26]，属于近海区域，因此采用其模拟海洋潮汐波流更加合理。

本文采用二阶斯托克斯非线性潮波方程模拟动态海浪的作用，通过在海洋域进口侧给定波流场的速度分布边界条件来进行数值模拟[27-30]，波的速度边界条件如式（2）～（5）所示。

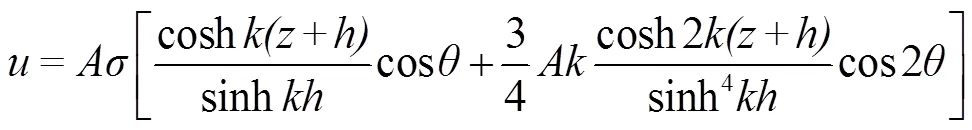
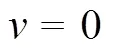
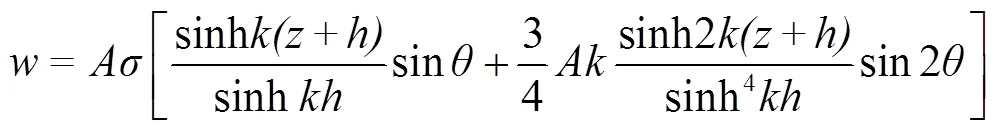
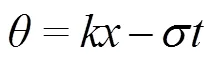
式中为潮波波高，m；为方向速度，m/s；为方向速度，m/s；为方向速度，m/s；为水深，m；为波面距离平均海面的距离，m；为波入射位置，m；为时间，s；为波数，rad/m；为圆频率，Hz；为相位函数，rad。

本文所研究的潮汐能水轮机[31]海洋侧入口处水深约为7.97 m，潮波波高按正常海浪等级选取了代表轻浪的1 m。设定波流进入流场位置处=0，潮波周期wave= 4 s。反向流动工况计算时，海洋域进口同样设置为斯托克斯二阶波流速度边界，方向为从海洋域进口指向水轮机出口，贯流机组域中反向过流时的出口给定为平均静压边界，平均静压数值根据反向发电时的尾水位进行计算。无论正向流动或反向流动，整体计算域都设定为水、气两相流动计算域，两相流计算模型采用均质模型，在计算过程不考虑气液相间质量转换，且海洋域进口处的斯托克斯二阶波流速度只针对水体进行设置，空气的速度给定为0。在海洋域中，基于流体体积分数法（Volume of fluid, VOF）模拟海水和空气分界的自由液面，海洋域的顶部开口设置为敞开式边界，同时给定平均相对静压为0（以1个大气压为基准）。海洋域的内外两侧对称面设置为对称面边界，底部和坝体面设置为无滑移固壁面。在整个计算域中都设置了重力效应，用以在数值模拟中更好的体现潮波对水轮机转轮力特性的影响。在整个计算域中，仅转轮域为旋转域，转轮域与其他固定域之间采用动静交界面连接。

由于潮波运动是随时间不断变化的瞬态运动，所以需要采用瞬态计算方法模拟潮波流动对水轮机水力性能的影响。动态潮波作用下的瞬态计算需要以定常计算结果为初始值，因此本文在开展动态潮波瞬态计算前先进行了无波流、恒定自由液面且无重力条件下的机组性能分析，以该结果为初始值再进行动态潮波作用下的双向贯流式水轮机瞬态计算。瞬态计算需要设置合理的时间步长Δ，由于潮波的周期大于转轮的旋转周期，为在合理的计算时间成本内捕捉潮波完整的流动信息，经过对时间步的测试计算，确定在正向流动和反向流动计算中都选择时间步长Δ=0.02 s，该时间恰好与转轮旋转15°的时间相同，同时也是波周期时间的0.005倍。湍流模型选择为RNG-模型，在瞬态计算的每个时间步内设置收敛准则为最大残差小于10-3，数值计算采用商业CFD软件ANSYS CFX来完成。

2 结果与分析

2.1 潮波对贯流式机组内涡量场的影响

为了研究潮波对贯流式机组内部涡量场的影响，在图6中给出了一个潮波周期内机组内部涡量场的变化。图6中的流场主要分为海洋域外流场和贯流机域内流场两个部分，外流场是模拟潮波产生的主要区域，同时，在图6的流体介质体积分数分布中，蓝色部分代表空气体积分数为1，红色部分代表水的体积分数为1，中间界面则表示气液两相分界面。从图6中可以看出，整个波流周期内，等涡量面的变化受波流周期的影响。图6a所示的=0时刻，潮汐波流未出现，内、外流场流动状态平稳；图6b所示=1/4wave时，潮汐向贯流机组域进口推移，造成短时间内流场涡量剧增；图6c所示=1/2wave时，内流场涡量却相比之前开始减小，海面下过流周期先于波流运动周期完成；图6d所示=3/4wave时，第二波峰即将进入外流场，内流场过流状态基本恢复到第一周期前水平。然后第二波峰进入流场，开始下一个波流周期。

在反向发电工况下，转轮室前再无其他导水机构，伴随潮汐波流大量涌入的海水将直接冲击转轮桨叶使转轮叶片受到的轴向力增大。由于波流对水体具有周期性推动作用，因此水轮机转轮的迎流侧会承受周期性的轴向作用力。此外，由于重力效应的影响，转轮在周向不同的位置时会承受不同的水压力，最终，周向和轴向作用力的叠加造成了转轮叶片转动过程中的非稳态受力特性，大大降低了工作在实际海洋能潮汐波流条件工况中的贯流式水轮机叶轮的疲劳寿命。在图7中给出了波流一个完整周期内波峰撞击坝体正壁面后对后续波流的干扰和叠加过程。

注：蓝色部分代表空气体积分数为1，红色部分代表水的体积分数为1，中间界面则表示气液两相分界面。图6a左侧为整体计算域内的气液两相分布,右侧为机组内部的等涡面形态，余同。

图7 潮汐波流反射过程

从图7中可以发现，波流在与坝体发生碰撞后损失了大部的动能，形成反射波流。如图7a所示。反射波流与后续跟随的波流相互覆盖，形成包裹空气的夹气涡旋，随即进入海洋内部。被覆盖在液面下的夹气涡将按照潮波水质点的运动轨迹，呈螺旋形随波流起伏前进，一部分夹气涡会在前进的过程中上升至水体表面而消散。有些夹气涡因水体流动作用撞击坝体正壁面被打散成更为细小的涡，这些碎涡将有部分随波流运动被卷入贯流机内流场。如图7b、7c所示。在被反射波覆盖而进入液面以下较深层的夹气涡会直接被波流带入内流场里，而这些夹气涡也因自身密度小，流动速度慢，逐渐向内流场上壁面区域聚集并黏附于整个内流场通道上侧，甚至还会与后续夹气涡合并形成一个类条形的低密度空腔，这种空腔最终将发展成为一条贯穿整个内流场上壁的低密度扁平流层，如图7d所示。这样的夹气涡分布压缩海流的过流面积，改变了贯流式机组内部流场从而影响其水力性能。尤其在转轮区域，流动条件复杂，夹气涡的空腔带也会因转轮的转动、叶顶间隙流动等因素在转轮室附近被切割打散，进而使得夹气涡经过转轮后不再紧靠上壁，而是分布在更广泛的区域，从而对机组的内流场造成更大的影响。

2.2 潮波对贯流式机组外特性的影响

图8为在海洋波流条件下的潮汐能贯流式水轮机组的出力情况。

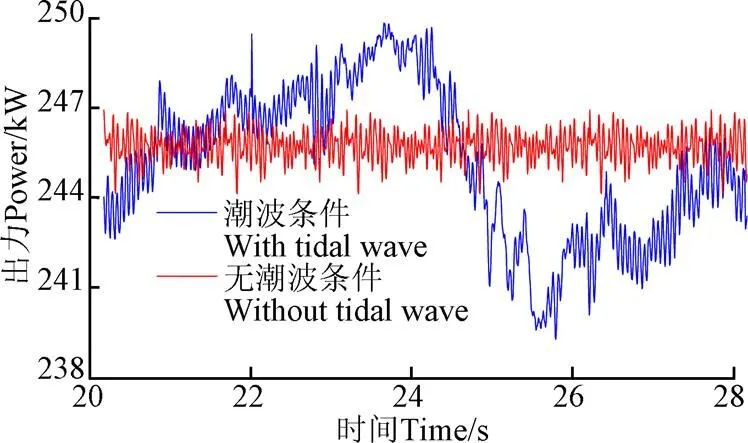
图8 贯流机组出力对比

从=20 s到=28 s为潮汐波流的第6和7个周期，反射波流及海流夹气涡等因素在流场中的影响已经充分体现在机组出力的波动上。从图中可见，贯流机组的出力在波流周期条件的影响下具有明显的波动，峰值达到249.85 kW，谷值达到239.28 kW，出力波动幅度达到3.86%；而对应在无波流的情况下，出力波动不足1%。两种条件下出力均值相差不足0.5 kW，但无波流条件出力标准差为0.51 kW，含波流条件为2.55 kW。这种差异主要来自于潮波流动中，波峰波谷交替使得内流场水推力随潮波流动的过程而变动，造成本工况中含波流出力差值高达10.48 kW，如此大的出力波动必然造成水轮机组效率的波动，并导致机组输出电能质量下降。

图9给出的是水轮机转轮单个叶片的力变化。海洋潮汐波流从=0时刻开始进入流场。夹气涡在流场中的发展按照时间和流场漩涡现象分为了2个部分：夹气涡刚刚流进入内流场和转轮室（图9a）和大量夹气涡进入转轮室（图9b）。结果表明，流场内夹气涡的发展会对贯流式机组的受力和工作情况产生明显的影响。如图9a所示，在=8 s 到17 s之间，贯流机内流场经历了从第一个夹气涡进入尾水管至夹气涡通过转轮室的过程，整个过程叶片的受力变化在夹气涡到达转轮室前相对稳定，在第=11.91 s时，第一个夹气涡进入转轮室之后之间表现出因受力不均而产生的波动。图9b则表现出了从=18.02 s开始，大量夹气涡涌入转轮室加剧了机组叶片受力波动变化的情况。

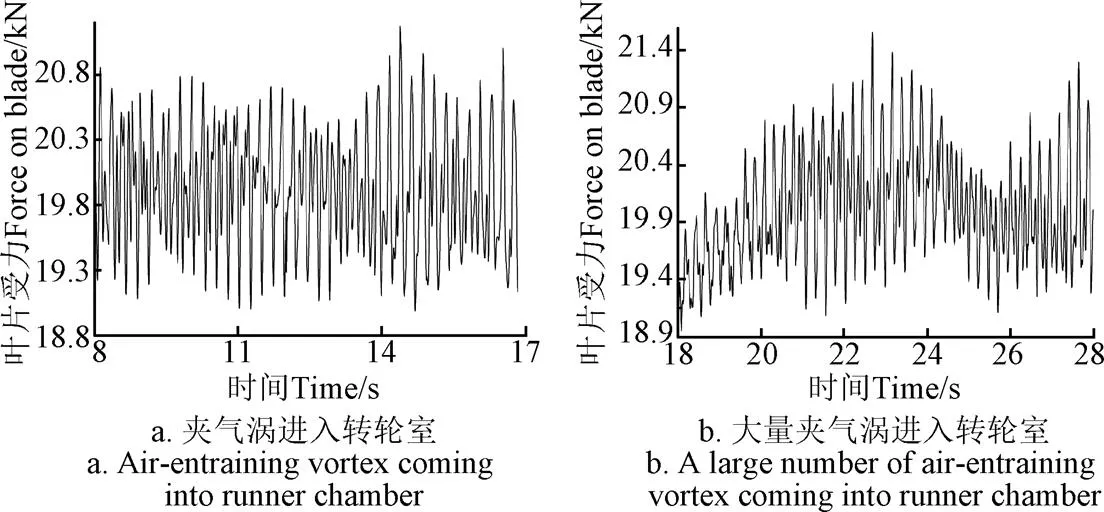
图9 不同时间段内单个转轮叶片上受力变化

图10给出了不同时间段内波流耦合与夹气涡共同作用下的叶片受力的频谱图。从图中可以看出，当夹气涡大量进入转轮室后，叶片的受力情况也受到了明显影响。波流频率（=0.25 Hz）所对应的受力的幅值增长了6.27倍。通过对比发现，当潮波作用和夹气涡影响加剧时，转轮叶片上所承受的脉动力具有明显的向低频移动的趋势，低频对应的幅值也会随着这种流动现象的发展而逐渐增大。

图11给出了夹气涡发展过程中的一个周期内两个时刻的流场变化。在考虑波流耦合影响的前提下，海洋来流潮波每一次撞击坝体壁面时都会损失较大能量，产生反向运动的反射波对后续波流造成影响，减小水体流动速度从而降低叶片受力。随着越来越多的夹气涡进入流场，在尾水管顶部形成了一个低压低速的夹气涡流动带。同时，夹气涡主要由反射波流对后续波流的覆盖作用产生，流场内夹气涡的流动改变等现象也均出现在不同时刻反射波作用之后。可见壁面反射波流影响了夹气涡流动从而改变流场流动性质，是机组性能变化的主要原因之一。

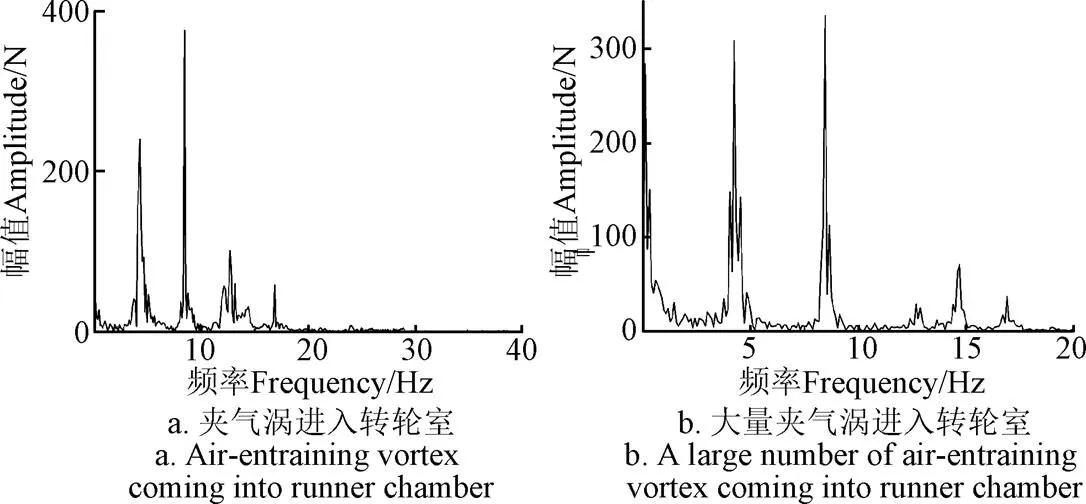
图10 单个转轮叶片受力频谱分析

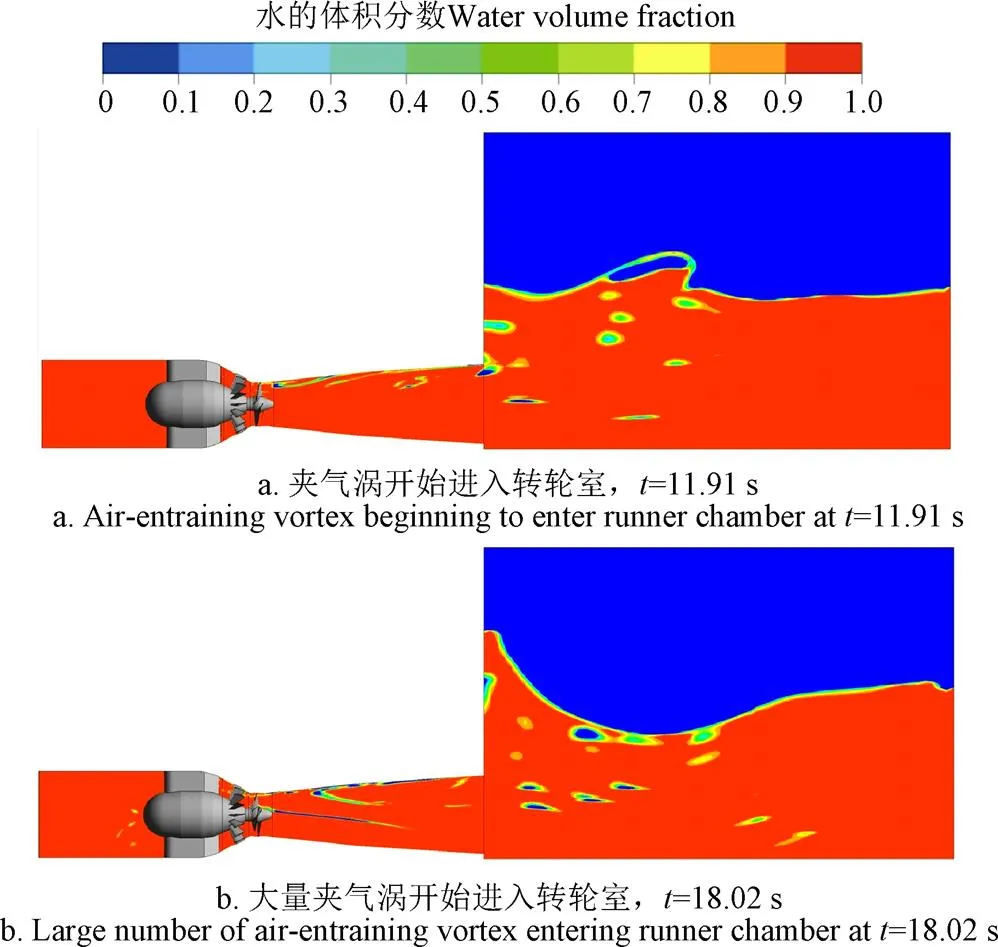
图11 两个典型时刻下夹气涡在计算域内的分布

3 结 论

本文以工作在海洋波浪条件下的潮汐能贯流式水轮机为对象，研究了二阶斯托克斯非线性潮波对机组内流场特性及外特性的影响，主要结论如下：

1）建立了二阶斯托克斯非线性潮波边界下的潮汐贯流式水轮机性能分析模型并通过试验数据验证了模型的可靠性。依据该模型进行研究发现，潮波对贯流式机组内部的涡量场产生了明显的周期性影响，表明机组内部的实际流场是随着潮波的发展而不断变化的非稳态流场，因此，在数值模拟中考虑潮波的影响能更好的反映潮汐贯流式机组实际运行时的内部流动细节。

2）反向运行时，潮波与机组入水口上方坝体碰撞反射后再与新的入射波相互作用是形成夹气涡的主要原因，这些夹气涡会在潮波的包裹下进入机组的内部从而对机组的性能造成影响。

3）潮波的周期性作用以及进入流场的夹气涡会导致潮汐贯流式机组的出力产生幅度达3.86%的波动，远高于无波流作用下的不足1%；同时，大量夹气涡进入流场还会造成单叶片所受脉动力中的低频成分增强，对叶片的强度性能造成不利的影响。

[1] 富旭平，郑峰. 灯泡贯流式水轮机效率问题[J]. 水电能源科学，2008(6)：132－133.

Fu Xuping, Zheng Feng. Study on efficiency of bulb turbine[J]. Water Resources and Power, 2008(6): 132－133. (in Chinese with English abstract)

[2] 刘胜柱，赵亚萍. 3叶片贯流水轮机内部流动数值与试验研究[C]//中国水力发电工程学会，2013.

Liu Shengzhu, Zhao Yaping. Numerical and experimental research on internal flow of three-blades[C]//Turbine China Hydroelectric Engineering Society, 2013. (in Chinese with English abstract)

[3] 钱忠东，魏巍，冯晓波. 灯泡贯流式水轮机全流道压力脉动数值模拟[J]. 水力发电学报，2014，33(4)：242－249.

Qian Zhongdong, Wei Wei, Feng Xiaobo. Numerical simulation of pressure pulsation in the whole flow passage of bulb turbine[J]. Proceedings of the Society of Hydroelectric Power, 2014, 33(4): 242－249. (in Chinese with English abstract)

[4] Thaithacha Sudsuansee，Udomkiat Nontakaew. Simulation of leading edge cavitation on bulb turbine[J]. Songklanakarin Journal of Science and Technology, 2011(1): 51－60.

[5] 刘延泽，常近时. 重力场对灯泡贯流式水轮机流场分析及水力性能评估的影响[J]. 水利学报，2008，39(1)：96－102.

Liu Yanze, Chang Jinshi. Influence of gravity on flow field analysis and hydraulic performance evaluation of bulb turbine[J]. Journal of Hydraulic Engineering, 2008, 39(1): 96－102. (in Chinese with English abstract)

[6] 王正伟，杨校生，肖业祥. 新型双向潮汐发电水轮机组性能优化设计[J]. 排灌机械工程学报，2010(5): 417－421.

Wang Zhengwei, Yang Xiaosheng, Xiao Yexiang. Hydraulic performance optimization of bidirectional tidal power turbine[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010(5): 417－421. (in Chinese with English abstract)

[7] 王正伟，周凌九，陈炎光，等. 灯泡贯流式水轮机水力损失分析[J]. 大电机技术，2004(5)：40－43.

Wang Zhengwei, Zhou Liangjiu, Chen Yanguang, et al Hydraulic loss analysis in bulb turbine[J]. Large Electric Machine and Hydraulic Turbine, 2004(5): 40－43. (in Chinese with English abstract)

[8] 赵亚萍. 轴（贯）流式水轮机性能研究与优化[D]. 西安：西安理工大学，2014.

Zhao Yaping. Performance Analysis and Optimization Design for Kaplan and Bulb Turbines[D]. Xi’an: Xi’an University of Technology, 2014. (in Chinese with English abstract)

[9] Soohwang A, Xiao Yexiang, Wang Zhengwei, et al. Numerical prediction on the effect of free surface vortex on intake flow characteristics for tidal power station[J]. Renewable Energy, 2017, 101: 617－628.

[10] Soohwang A, Xiao Yexiang, Wang Zhengwei, et al. Performance prediction of a prototype tidal power turbine by using a suitable numerical model[J]. Renewable Energy, 2017, 113: 293－302.

[11] Lane G L, Rigby G D, Evans G M. Pressure distribution on the surface of Rushton turbine blades-experimental measurement and prediction by CFD[J]. Journal of Chemical Engineering of Japan, 2001, 34(5): 613－620.

[12] 李琪飞，张毅鹏，敏政，等. 变工况下贯流式水轮机叶片形变分析[J]. 兰州理工大学学报，2015，41(2)：61－64.

Li Qifei, Zhang Yiping, Min Zheng et al. Deformation analysis of tubular turbine blades under variable working condition [J]. Journal of Lanzhou University of Technology, 2015, 41(2): 61－64. (in Chinese with English abstract)

[13] 郑小波，王玲军，翁凯. 基于双向流固耦合的贯流式水轮机动力特性分析[J]. 农业工程学报，2016，32(4)：78－83.

Zheng Xiaobo, Wang Lingjun, Weng Kai. Dynamic characteristics analysis of tubular turbine based on bidirectional fluid-solid coupling[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(4): 78－83. (in Chinese with English abstract)

[14] 王正伟，阎宗国，彭光杰，等. 一种六工况双向潮汐发电水轮机：CN202140236U[P]. 2012-02-08.

[15] 李正贵，任明月，杨逢瑜. 水位变化对贯流式水轮机组出力及稳定性影响[J]. 水力发电学报，2017，36(7)：74－82.

Li Zhenggui, Ren Mingyue, Yang Fengyu. Effects of changes in water levels on power output and stability of tubular turbine sets[J]. Journal of Hydroelectric Engineering, 2017, 36(7): 74－82. (in Chinese with English abstract)

[16] 王树青，梁丙臣. 海洋工程波浪力学[M]. 青岛：中国海洋大学出版社，2013.

[17] 赵理工，梁书秀. 波流耦合作用下台风浪的模拟[J]. 中国水运,2016，16(6)：100－103.

Zhao Ligong, Liang Shuxiu. Wave Simulation under Wave-Current Coupling[J]. China Water Transport,2016, 16(6):100-103. (in Chinese with English abstract)

[18] Luo Yongyao, Wang Zhengwei, Xiao Yexiang, et al. Optimization of the runner for extremely low head bidirectional tidal bulb turbine[J]. Energies, 2017, 10(6): 787－799.

[19] Luo Yongyao, Wang Zhengwei, Xin Liu, et al. Numerical prediction of pressure pulsation for a low head bidirectional tidal bulb turbine[J]. Energies, 2015, 89: 730－738.

[20] 邹志利. 海岸动力学[M]. 北京：人民交通出社，2009.

[21] 王福军. 计算流体力学-CFD 软件原理与应用[M]. 北京：清华大学出版社，2004.

[22] 吴玉林，刘树红，钱忠东. 水力机械计算流体动力学[M]. 北京：中国水利水电出版社，2006.

[23] 刘树红，吴玉林. 水力机械流体动力学基础[M]. 北京：中国水利水电出版社，2007.

[24] 王福军. 流体机械旋转湍流计算模型研究进展[J]. 农业机械学报，2016，47(2)：1－14.

Wang Fujun. Research progress of computational model for rotating turbulent flow in fluid machinery[J].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(2): 1－14. (in Chinese with English abstract)

[25] IEC-60193. Hydraulic turbines, storage pumps and pump-turbines model acceptance tests[S].

[26] 杨爱菊，杨丽洁，李红星，等. 海洋能之潮汐电站开发技术概要—浅析潮汐电站选址基本要素[J]. 西北水电，2010(2)：89－95.

Yang Aiju, Yang Lijie, Li Hongxing, et al. An overview of technology for development of tidal power stations-Analysis of basic elements for site selection of tidal power stations[J]. Northwest Hydropower, 2010(2): 89－95. (in Chinese with English abstract)

[27] 刘莎莎，顾煜炯，惠万馨，等. 基于边界造波法的波浪数值模拟[J]. 可再生能源，2013，31(2)：100－103.

Liu Shasha, Gu Yujiong, Hui Wanxin, et al. Wave numerical simulation based on wave-generation method of defining inlet boundary conditions[J]. Renewable Energy Resources, 2013, 31(2): 100－103. (in Chinese with English abstract)

[28] 于龙基，杨森，张华昌，等. 弧形防浪墙的迎浪面波压力数值模拟[J]. 水运工程，2017(11)：29－35.

Yu Longji, Yang Sen, Zhang Huachang, et al. Numerical simulation of wave pressure on upright section of arc crown wall[J]. Port and Waterway Engineering, 2017(11): 29－35. (in Chinese with English abstract)

[29] 刘师辉，胡金鹏. 基于Fluent的数值造波及其对水平板冲击作用初步研究[J]. 广东造船，2017，36(6)：13－16.

Liu Shihui, Hu Jinpeng. A preliminary study on numerical waves and its impact on horizontal plate with fluent[J]. Guangdong Shipbuilding, 2017, 36(6): 13－16. (in Chinese with English abstract)

[30] 刘秀丽，段梦兰，高攀，等. 基于OpenFOAM的数值波浪水槽研究[J]. 复旦学报：自然科学版，2015，54(3)：373－378.

Liu Xiuli, Duan Menglan, Gao Pan, et al. Development of numerical wave flumes based on openfoam[J]. Journal of Fudan University: Natural Science, 2015, 54(3): 373－378. (in Chinese with English abstract)

[31] 乐清湾水利开发委员会. 江厦潮汐试验电站:1969-2005 [M]. 北京：中国电力出版社，2008.

Effect of second-order Stokes nonlinear tidal wave on performance of tidal tubular turbines

Feng Jianjun, Zhu Guojun※, Wang Zhun, Wu Guangkuan, Luo Xingqi

(710048,)

As a form of ocean energy, tidal energy is extremely abundant in oceans, with the characteristics of being clean, reliable, predictable and renewable. In the development of tidal energy, a bi-directional tubular turbine has been widely adopted for power generation. The tubular turbine converts the energy extracted from tides into mechanical energy, and further into useful electricity. The tubular turbine has been well designed suitable for generating power from both flow directions, in order to take full use of the tidal energy not only in the flood tide state but also during the ebb tide state. However, the operation condition of the tubular turbine will be definitely affected by the movement of the wave caused by tide, especially for the reverse power generation direction in which the flow direction is from the ocean to the turbine installed in the hydraulic dam. In this case, under the influence of ocean wave current conditions, the change of hydrodynamic performance during the reverse operation of tidal energy units is an important issue to be considered during the development of tidal energy units. In this paper, the nonlinear second-order Stokes wave law was used to simulate the ocean tide flow, and the second-order Stokes wave formula ocean wave flow condition model has been established based on actual oceanic flow conditions. The chosen tubular turbine had 4 runner blades, with a hub ratio of 0.38 and a runner diameter of 2.5 m. The turbine consisted of an intake part with body, guide vanes, runner and straight draft tube. In order to discrete the computational domains, the grid generation tool ICEM CFD was used to generate high quality structure grids. The number of grids chosen for simulations was approximately 6.5 million, after a grid-independent study with the hydraulic efficiency of the turbine being the examined criterion. The RNG-. turbulence model was chosen to close the time-averaged N-S equations. Transient simulations with considering the effect of the ocean wave on the flow have been realized with the help of ANSYS CFX, with a VOF (volume of fluid) model being adopted in the ocean domain to simulate the free surface of the boundary between the liquid and air. Based on the numerical results, the internal flow characteristics of a tidal energy turbine tune turbine in reverse running under dynamic wave flow boundary conditions were studied. In addition, the influence mechanism of tidal wave on the stability of the tubular turbine operation was discussed in detail. The results showed that: 1) Considering the coupling of wave and flow, most of the kinetic energy was lost after the tidal wave collided with the dam, and the reflected wave flow was therefore formed, which covered the air before the next peak of the wave and produces bubbles entering into the interior of the ocean. 2) The interaction between the incoming tidal wave and the reflected tidal wave on the wall of the dam was the cause of the vortex at the water intake of the tidal tubular turbine. The formed vortex was rotated under the liquid surface and flows into the internal flow field. The upper side of the flow path compressed the flow area to form a low-pressure and low-speed vortex region, which changed the flow distribution of the internal flow field and the characteristics of the tubular turbine. 3) The action of the dynamic wave caused the force on the rotor blades of the tidal tubular turbine to fluctuate greatly, and the low-frequency amplitude of the blade force increases with the development of the air-entraining vortex. At the same time, the fluctuation of unit output under the influence of wave current reached 3.86%, which was much higher than that of less than 1% under no-wave condition, resulting in a decline in power quality.

turbines; models; computer simulation; wave-flow coupling; hydraulic performance; air-entraining vortex

10.11975/j.issn.1002-6819.2019.02.007

TK733+.8

A

1002-6819(2019)-02-0048-07

2018-07-17

2018-12-10

国家自然科学基金项目（51339005，51679195，51479167）；陕西省自然科学基础研究计划资助项目（2018JM5102）

冯建军，博士，教授，博导，研究方向为流体机械流动理论及优化设计、流体机械振动与稳定性分析。Email：jianjunfeng@xaut.edu.cn

朱国俊，博士，讲师，研究方向为研究方向为流体机械流动理论及优化设计、流动分析等。Email：zhuguojun@xaut.edu.cn

冯建军，朱国俊，王 准，吴广宽，罗兴锜. 二阶斯托克斯非线性潮波对潮汐贯流式水轮机性能的影响[J]. 农业工程学报，2019，35(2)：48－54. doi：10.11975/j.issn.1002-6819.2019.02.007 http://www.tcsae.org

Feng Jianjun, Zhu Guojun, Wang Zhun, Wu Guangkuan, Luo Xingqi. Effect of second-order Stokes nonlinear tidal wave on performance of tidal tubular turbines[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(2): 48－54. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.02.007 http://www.tcsae.org