无轴承磁通切换电机转矩及悬浮力解析计算
郑梦飞,周扬忠
(福州大学,福州 350108)
0 引 言
定子永磁磁通切换电机(以下简称FSPMM)相较于传统永磁体转子的永磁同步电机而言,由于永磁体放置于定子侧,转子由硅钢片简单叠压而成,具有结构简单可靠,散热容易,转矩密度高等优点[1-4]。因此,将无轴承技术应用到传统FSPMM中,即无轴承磁通切换电机(以下简称BFSPMM), 在保有无轴承技术所带来的无需机械轴承,无需润滑,定转子之间完全隔离等优点前提下[5-6],克服了传统无轴承永磁电机在一些应用场合下转子为一次性使用费用高及永磁体高温退磁等缺陷[7-8],在生物医药、半导体及化学化工领域具有广阔的应用前景。
回顾传统FSPMM的一般分析方法,对于BFSPMM的研究可借助于FSPMM相关理论分析方法。然而,由于在FSPMM中永磁体位于定子侧,且定转子均为凸极结构,传统成熟的永磁同步电机理论无法直接应用。目前,学术界对于双凸极气隙研究方法主要分为有限元分析法[9]、等效磁网络分析法[10]、基于磁动势-磁导分析法[11]、子域法[12]、空间离散法[13]、许-克变换[14-15]、傅里叶分析法[16]等方法。其中,有限元与等效磁网络分析方法应用最为广泛,但存在模型构造复杂且计算时间长等问题;子域法和基于磁动势-磁导分析法及傅里叶分析法虽然均能得到双凸极气隙磁密的解析表达式,但由于涉及到大量的解方程等复杂代数运算,实际应用不多。相较而言,许-克变换计算简单、模型构造方便且物理概念更加清晰,已逐渐成为双凸极气隙主流分析方法之一。
目前,无轴承技术已经成功应用到几乎所有的电机,相关理论分析及数学模型构建已经十分成熟。然而,综合已发表的BFSPMM相关文献,BFSPMM相关理论分析、悬浮力与电磁转矩模型构建大部分仍然是借助于有限元分析[17-19]与等效磁网络[20],因此,存在计算时间长且模型构造复杂等缺陷。同样,由于无法得到气隙磁密解析表达式,其对于电机结构参数十分敏感,电机结构的细微更改均将带来大量的模型重建工作及计算时间,所得到的相关数学模型不具有实际通用性。
基于此,本文借助传统FSPMM中基于许-克变换的双凸极气隙分析方法,推导出电机关键电磁参数的解析表达式,并基于磁齿轮效应与麦克斯韦张量法分别构建BFSPMM中转矩及悬浮力的数学模型。最后,利用有限元仿真结果验证了所推导的解析模型的正确性。
1 六相单绕组BFSPMM拓扑结构及悬浮力生成原理
1.1 拓扑结构
本文所研究的BFSPMM为12/10结构,单绕组连接方式,其拓扑结构如图1所示。电机定子由12块U形铁心构成,且相邻两个U形铁心夹着沿切向交替充磁的永磁体,而转子由硅钢片简单叠压而成,有10个齿。电机六相绕组电流iA~iF同时含有控制转子切向旋转的电流iAT~iFT和控制转子径向悬浮的悬浮电流iAS~iFS。定义三相悬浮电流iAD、iBE与iCF,悬浮电流iAS~iFS满足iAS=iDS=iAD,iBS=iES=iBE,iCS=iFS=iCF。
T6恒功率变换矩阵如下:
(1)
可将六相绕组相电流分解到控制转矩输出的转矩平面电流iαTiβT,控制悬浮力输出的悬浮力平面电流iαSiβS与零序平面电流io1io2:
因此,由式(2)可知,按照如图1所示的绕组连接方式,电机六相绕组转矩生成部分可以等效为六相对称绕组A~F通入的转矩电流iAT~iFT;而悬浮力生成部分可以等效为三相悬浮绕组AD,BE与CF相(由A相与D相,B相与E相,C相与F相分别构成)通入对称的悬浮电流iAD,iBE与iCF得到。

图1 BFSPMM横截面图
1.2 悬浮力生成原理
以AD相绕组为例,在图1的转子位置角处,4个气隙定转子重叠面积相等,且电机气隙圆周关于电机中心点处处对称,故由iAD在4个气隙处生成的磁通均相等,令其为ΦAD。相对于永磁磁通ΦPM,其中气隙1与气隙3总磁通增大为ΦPM+ΦAD,而气隙2与气隙4总磁通减小为ΦPM-ΦAD。故由麦克斯韦张量法可知,此时电机将受到在空间上近似为45°圆周角方向的磁拉力。同理分析由BE,CF相悬浮电流电流iBE,iCF生成的磁拉力,用矢量图表示如图2所示。由图2可知,三相悬浮电流生成的悬浮力空间对称,因此通过通入合适的悬浮电流即可产生沿空间对应方向及大小的悬浮力。

图2 AD,BE和CF相产生的悬浮力空间矢量图
2 气隙磁密分布
2.1 气隙磁导分布
为使许-克变换应用于BFSPMM中,本文设定以下前提条件:电机定转子铁心相对磁导率为无穷大;定转子槽为无穷深结构;铁心上相邻的两个槽之间不存在耦合;电机气隙磁密分布沿径向保持不变。
对于定子永磁型的BFSPMM而言,由于定子铁心不完整,气隙不为闭合区域,无法直接应用许-克变换将双凸极气隙映射至隐极气隙。若采用导磁桥形式将定子铁心构成整体,由于导齿桥饱和,不满足铁心相对磁导率为无穷大的前提条件。然而,即使定子铁心为整体且不饱和,由于双凸极结构,气隙闭合区域顶点数超过4个,将难以得到许-克变换解析表达式,需要借助相关数值算法逼近,将耗费大量的计算时间。
另一方面,双凸极气隙磁导可以表示[21]:
式中:θ为电机气隙圆周角;θr为电机转子位置角;Λs(θ)为仅有定子凸极时气隙磁导分布;Λr(θ,θr)为仅有转子凸极时气隙磁导分布;Rsi与Rro分别为电机定子内径与转子外径;μ0为真空磁导率。
因此,对于BFSPMM而言,分别计算仅考虑定子凸极效应与转子凸极效应下的气隙磁导分布,由式(3)就可以计算得到电机气隙磁导分布。
以电机定子凸极而转子为光滑圆柱体为例,在z平面,电机定子单个槽模型如图3(a)所示。为简化模型,利用式(4)将其映射至w平面时保持w1w2平行于w1w5,满足铁心槽无限深的前提条件。如图3(b)所示,g可由式(5)计算得到。
(4)

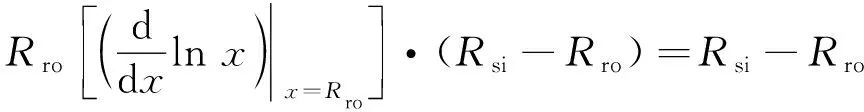
为将点t1-t5映射至点w1-w5,t平面的上半平面映射至w平面的气隙区域,如图3(c)所示,利用式(6)的许-克变换公式:
式中:
(7)


(a) z平面

(b) w平面
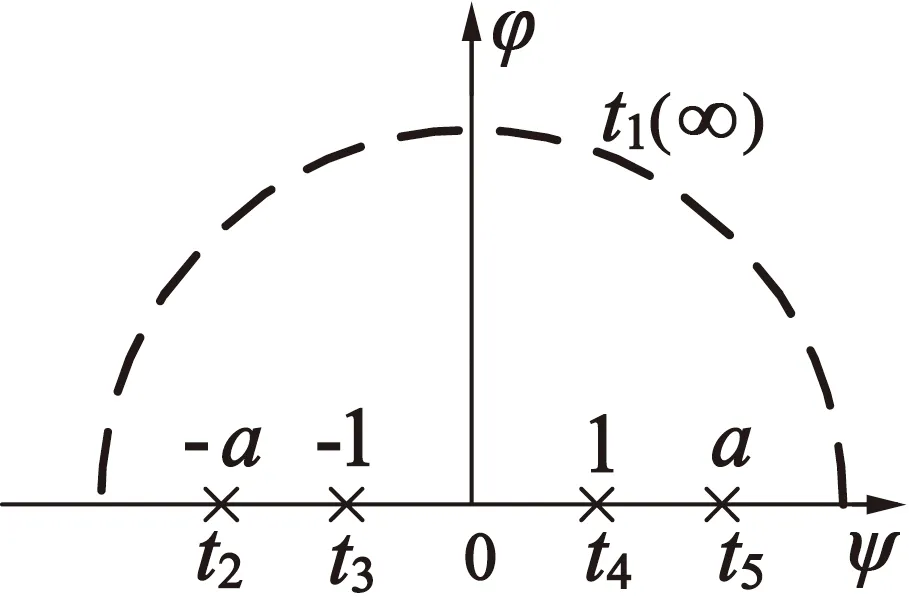
(c) t平面
在t平面中的上半平面,若满足正负实轴上磁势均恒定,且二者相差fm的狄利克雷边界第一边界条件,则其磁动势分布:
(9)
图3(b)中狄利克雷第一边界条件:定子齿表面磁动势为fm,而光滑转子表面磁动势为0,对应t平面中t1t2t3与t4t5t1表面磁动势为fm,而t3t4表面磁动势为0,即沿正实轴方向在t=-1处磁势减小fm,而在t=1处增大fm。因此,由式(9)可知,图3(c)中t平面磁动势分布:
(10)
t平面磁密Bt:
(11)
因此,z平面磁密:
(12)
考虑到前文所述的前提条件,将式(12)简化:
(13)
式(13)中存在t平面变量,为得到z平面的磁导表达式,需要求解式(6)的反函数。然而,该反函数难以推导得到,因此,无法直接得到气隙磁密的解析表达式。由于单个槽下单凸极气隙磁导分布可以表示[21]:
(14)
式中:α0与αt分别表示槽宽及齿距机械角,如图3(b)所示,β按照如下定义:
(15)
因此,借助式(1),仅需计算气隙最大磁密Bzmax与最小气隙磁密Bzmin,即可得到气隙磁密分布。
气隙最大磁密Bzmax在t=±1处取得:
(16)
气隙最小磁密Bzmin在t=0处取得:
(17)
故:
(18)
本文电机为12/10结构,将永磁体等效为气隙,电机定子U形铁心有24个齿,转子有10个齿。因此,由式(14)可知,仅考虑定子凸极效应时气隙磁密分布傅里叶级数展开:
(19)
式中:bs与τs分别为定子槽宽与齿距,βs为式(18)在定子侧的取值。
同理,仅考虑转子凸极效应时气隙磁导分布的傅里叶级数展开(任意一个转子槽中心线与z平面正实轴重合时即为转子初始位置):

式中:br与τr分别为转子槽宽与齿距,βr为式(18)在转子侧的取值。
由式(1),式(19)和式(20)即可计算双凸极气隙磁导分布Λrs(θ,θr)。
2.2 永磁气隙磁密
当定子齿不饱和时,相邻两个永磁体所夹的U形齿极靴上的磁动势相等且保持为恒值。因此,若利用Cater系数对定转子槽的齿槽效应进行补偿,可直接将BFSPMM双凸极气隙等效为隐极气隙求解气隙永磁磁势分布,如图4(a)所示。图4中定转子Carter系数分别表示为kcs与kcr,其分别可由式(21)和式(22)计算得到:
(21)
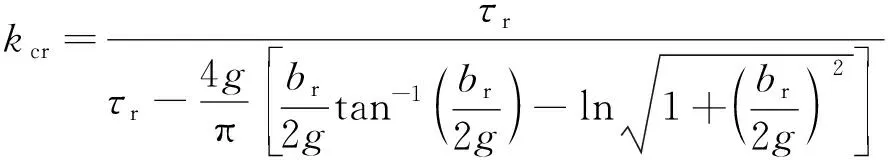
气隙沿圆周角θ分布的永磁磁动势Fpm如图4(b)所示,结合图4(a)可以计算得到Fm:
(23)
式中:Hc表示永磁体矫顽力;Rpm表示永磁体磁阻,其与R1与R2可由下式计算得到:
(24)
式中:τt表示相邻两个永磁体所夹U形铁心在气隙侧的切向长度,本文中τt=π/8。

(a) 等效磁路
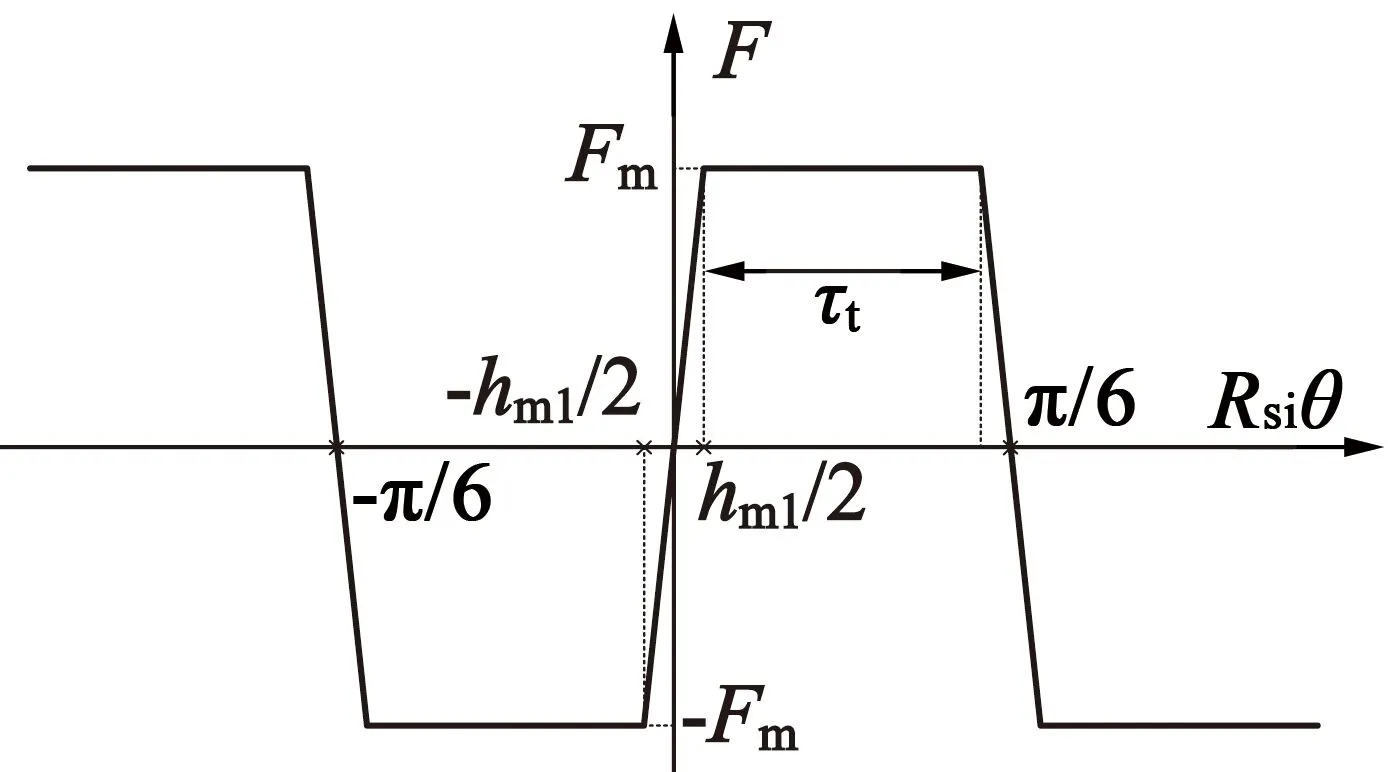
(b) 磁动势分布
因此,由图4(b)可知,永磁磁动势可用傅里叶级数展开:
sin[6(2n-1)θ] (25)
联立式(1),永磁气隙磁密分布可以表示:
Bpm(θ,θr)=Fpm(θ)Λrs(θ,θr) (26)
2.3 A相绕组电流气隙磁密
如图5(a)所示,用Carte系数对转子槽的齿槽效应进行补偿,将转子等效为圆柱体。以A1齿为例,类似于Fpm的推导过程,可以推导得到图5(b)中3个磁势幅值FAD1,FAD2及FAD3的值:
(27)
式中:Nc为电机相绕组匝数;R3与R4:
(28)

(a) 等效磁路

(b) 磁动势分布
考虑到A2齿沿圆周超前A1齿90°圆周角,因此由A相绕组电流iAD产生的磁动势的傅里叶级数展开可以表示:
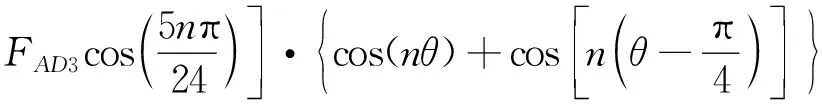
联立式(1),A相绕组电流iAD产生的气隙磁密分布可以表示:
BA(θ,θr)=FA(θ)Λrs(θ,θr) (30)
3 悬浮力与转矩数学模型
3.1 转矩数学模型
在无偏心情况下,由于悬浮电流产生的沿转子表面切向的洛伦兹力合力为0,因此BFSPMM转矩生成部分可以等效为传统FSPMM。但不同于传统永磁同步电机,FSPMM由于永磁体位于定子侧,定子电枢电流与永磁体产生的磁动势经转子调制在气隙中产生多种极对数的谐波,其中参与转矩输出的磁密极对数远不止一个。
为分析方便,定义pr为转子极对数,ps为定子永磁体极对数,Ωr为电机转子旋转机械角速度,对于本文所述的12/10 BFSPMM,pr=10,ps=6。
由电机定子侧永磁体生成的永磁磁势经过转子齿调制,在气隙中产生极对数为4,16,8,28(|kpr±(2i-1)ps|,k=1,i=1,2,…)的永磁磁密,在空间上均旋转同步于prΩr,因而绕组中感应出电角频率为prΩr的基波反电动势;由电角频率为prΩr的对称电枢电流产生的磁动势经过转子齿调制,在气隙中产生极对数为4,8,16,20(4q,q=3r-1或q=3r-2,r=1,2,…)的电枢电流磁密。二者在空间上旋转均同步于prΩr,如表1所示。表1中,负号表示旋转方向同转子旋转正方向相反。
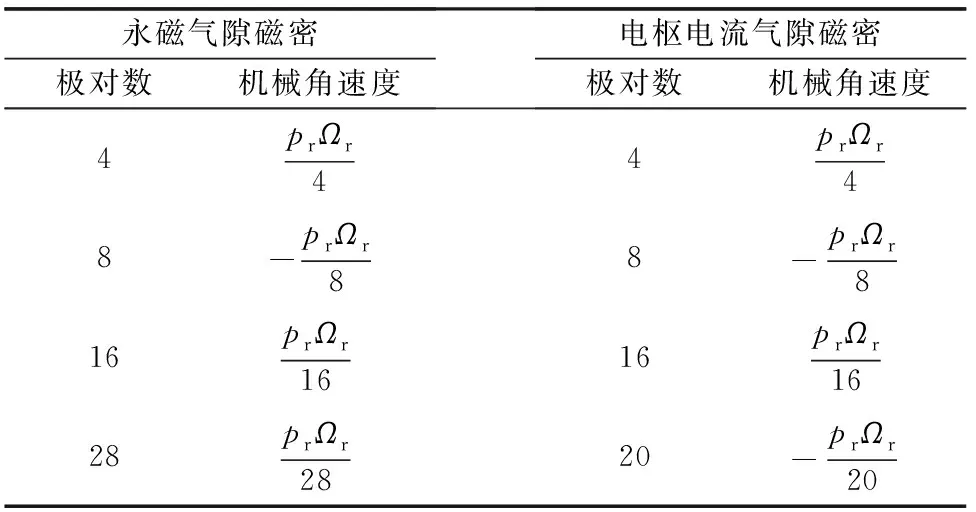
表1 气隙磁密极对数及其对应的旋转速度
由此可知,由电机绕组中对称电流在气隙中产生的旋转谐波磁密,其极对数正比于4,且同步于静止的永磁磁动势经转子基波磁导调制之后,极对数正比于pr-ps的旋转的永磁谐波磁密,该现象即体现为磁齿轮效应,即绕组极对数pw满足:
pr=ps+pw(31)
因此,可将FSPMM的功率部分等效为无穷多个极对数为4q(q=3r-1或q=3r-2,r=1,2,…),但相绕组反电动势频率均为prΩr/(2π)的永磁同步电机叠加,直接推导得到电机电磁转矩:
式中:ea~ef为相绕组反电动势;Irms为相绕组电流有效值;ψf为相绕组匝链的永磁磁链;φe为相绕组电流同反电动势相位差。
以A相绕组为例,借助式(26),ψf可以通过下式计算得到:
(33)
式中:Lstk为电机实际轴长。联立式(32)与式(26)即可得到电机电磁转矩解析表达式。
3.2 悬浮力数学模型
借助麦克斯韦张量法,电机转子轴向单位长度受到的径向电磁力Fsus可以表示:
(34)
本文取Γ1为在气隙中半径为Rh=(Rsi+Rro)/2的闭合圆周。在BFSPMM中一般气隙径向磁密Bn远大于切向磁密Bt。因此,考虑电机实际轴长Lstk,电机转子在x,y方向受到的电磁力可以分别表示:
(35)

以AD相为例,由图1可知,AD相通入电流iAD产生的气隙磁密沿电机中心径向对称的两侧分别为ΔBn与-ΔBn,且Bn也沿电机中心径向对称,因此产生的x方向悬浮力可表示:
同理,y方向悬浮力:
(38)
式中:Bn与ΔBn可分别由式(26)与式(30)计算得到。至此,本文完成了电机悬浮力及转矩的解析数学模型构建。
4 有限元仿真验证
为验证本文所推导的12/10 BFSPMM解析数学模型的正确性,按照表2构建BFSPMM有限元仿真模型。
首先按照式(33)计算A相绕组永磁磁链,每项傅里叶级数展开均取100项,其与有限元分析对比结果如图6所示。由图6可知,二者正弦度高,且相位基本一致,仅有幅值上不到6%的细小偏差,这主要是由于在永磁磁动势幅值计算过程中忽略了气隙磁密沿径向分布的细微差异及相邻两个槽之间的轻微耦合,在实际应用过程中可将二者影响忽略。

表2 电机结构参数

图6 A相绕组永磁磁链
图7表示电机AD相绕组通入单位正向悬浮电流时,由式(37)与式(38)计算得到的悬浮力与有限元分析之间的对比(傅里叶级数展开均取100项)。

(a) x方向

(b) y方向
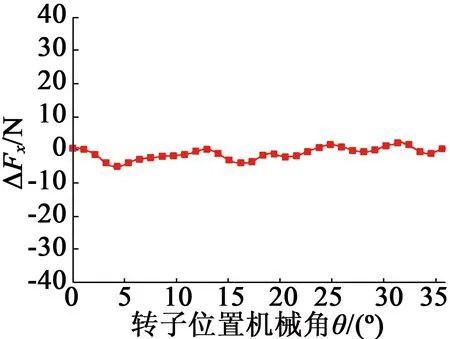
(c) x方向悬浮力计算误差

(d) y方向悬浮力计算误差
由图7可知,理论计算结果与有限元仿真结果之间误差很小;x,y方向悬浮力最大误差均不超过4 N,误差主要原因在于本文计算单凸极结构槽内磁导分布仅考虑其基波分量,忽略其高次谐波分量;解析模型成功计算出了电机悬浮力固有的很小的直流分量;理论与有限元仿真均表明,由于组成每相绕组的两个线圈在空间上正交,x,y方向悬浮力存在30°电角度相位差。
5 结 语
本文将许-克变换应用到具有双凸极气隙的BFSPMM中,推导并构建了其转矩及悬浮力解析数学模型,理论分析及有限元仿真结果表明:
1) 有限元仿真结果验证了该解析模型的正确性,电机永磁磁链及x,y方向悬浮力正弦度高;
2) 电机x,y方向悬浮力相位存在固有的30°电角度相位差;
3) 电机x,y方向悬浮力均存在很小的直流分量偏置,可以借助所提数学模型对电机结构进行进一步的优化将其影响降至最小。

