半干旱区垄沟集雨系统点尺度土壤水分动态随机模拟

尹鑫卫, 王 琦, 李晓玲, 吴 雪

1 中国科学院新疆生态与地理研究所, 阜康荒漠生态国家野外科学观测研究站, 乌鲁木齐 830011 2 中国科学院大学, 北京 100049 3 甘肃农业大学草业学院, 兰州 730070 4 甘肃农业大学水利水电工程学院, 兰州 730070

土壤水分是半干旱农田生态系统植物水分的主要来源,是养分循环和流动的载体,在土壤-植被-大气系统物质和能量转化中起着核心和纽带的重要作用[1]。同时土壤水分作为陆地水循环和水量平衡的一个重要组成部分,通过一种强烈的非线性方式控制着农田生态系统降雨在蒸散发、径流、入渗和渗漏等水分循环过程中的分配[2-3]。因此,认识半干旱农田生态系统与土壤水分关系和相互作用机理,对于揭示农田生态系统稳定性及其水土关键要素的变化过程具有重要意义[4]。

垄沟集雨系统利用田间起垄、沟垄相间、垄面产流、沟内高效集雨,并依靠增温、抑蒸等生理生态效应,已成为水分缺乏的半干旱区农田生态系统一项重要的集水节灌措施[5-7]。然而,受多种物 理、化学和生物过程以及降水、径流、地形、植被、土壤质地等不确定变量的影响,垄沟集雨系统土壤水分动态变化表现出较大的随机特性[8-12],这种随机属性决定了该系统土壤水分动态模型只有以概率形式描述才具有实际意义。Eagleson等[13]首次将随机理念纳入到土壤水分动态模型的研究中,建立了随机动力学水文模型,并推导计算了一次降水事件水量转化各要素的概率分布函数和数学期望值。随后众多学者[14-20]对土壤水分动态建立了随机数学模型,Rodriguez等[8]建立了时间尺度为1 d空间一点的土壤水平衡的概率模型,首次比较完整地考虑了随机输入项对土壤水分动态变化的影响,并输出了土壤水平衡随机微分方程的解析解,成为土壤水分动态随机模拟的一个里程碑。Laio等[17]通过改进Rodriguez模型蒸散发项,引进2个土壤水分临界值(凋萎系数和吸湿系数),使其能够在水分胁迫条件下更真实地描述土壤水分动态。Pan等[20]将土壤水分动态随机模型应用于华北平原农业灌溉区,将灌溉处理为降水事件,分析了冬小麦和夏玉米土壤水分的概率分布特征,并探讨了降水和灌溉与作物水分胁迫之间的关系。虽然目前土壤水分动态随机模拟研究已出现了大量的研究成果,但在我国半干旱农田生态系统相对较薄弱[21],尤其在半干旱区田间垄沟集雨系统中尚缺乏适用性探讨和深入研究。由于该系统土壤水分与微地形、降水、径流、蒸散发、植被、土壤特性及覆盖材料等密切相关[22-24],长期处于动态变化状态,且其变化过程比较复杂,因此有必要对该系统土壤水分动态进行模拟和研究。

本文利用中国气象局定西干旱气象与生态环境试验基地2012—2013年垄沟集雨燕麦生长季土壤水分观测数据及2000—2015年日降水资料,分析了研究区降雨量特征及其变化趋势；研究了不同覆盖材料和不同沟垄比对集雨垄径流量和土壤水分动态特征的影响；探讨了Laio土壤水分动态随机模型在研究区田间垄沟集雨系统的适用性,在此基础上获得了垄沟集雨系统燕麦生长季点尺度的土壤水分概率密度函数；同时对Laio模型涉及参数的敏感性进行了分析,以期为半干旱区垄沟集雨系统土壤水分动态模拟提供科学方法,为半干旱区农田生态系统水分高效利用及管理提供理论依据。

1 材料与方法

1.1 研究区概况

研究区位于中国气象局兰州干旱气象研究所定西干旱气象与生态环境试验基地(35°33′N,104°35′E,海拔1896.7 m)。该基地属黄土高原西部丘陵区和半干旱地区,具有典型的温带大陆性季风气候。年日照时间为2433 h；年平均气温6.7℃,年平均最高和最低气温分别为25.9℃(7月)和-13.0℃(1月)；平均无霜期140 d。1971—2014年平均降雨量388 mm,冬季和夏季月平均降雨量分别为20—80 mm和150—270 mm。降雨在年内分布极不均匀,7—10月降雨量占年降雨量的86.9%,蒸发强烈,年均潜在蒸发量达到1500 mm。试验地地势平坦,土壤为重壤土,0—100 cm土壤平均容重为1.38 g/cm3,田间持水量为25.6%,饱和含水量为43.87%,永久凋萎系数为6.7%,地下水埋深10.4 m,土壤水与地下水的水力联系微弱。当地耕作制度为1年1熟,主要种植作物有春小麦(Triticumaestivum)、燕麦(Avenasativa)和马铃薯(Solanumtuberosum)等,主要种植牧草有紫花苜蓿(Medicagosativa)和红豆草(Onobrychisviciaefolia)等。

1.2 试验设计

试验以燕麦(坝莜8号)为指示作物,采用田间垄沟集雨覆盖种植技术,垄覆盖作为集雨区,沟无覆盖作为种植区,小区随机排列,共设10个处理(3种沟垄比×3种覆盖材料+1平作),重复3次。3种覆盖材料分别为生物可降解膜、普通塑料膜和土壤结皮,3种沟垄比分别为60 cm∶30 cm、60 cm∶45 cm和60 cm∶60 cm(沟宽∶垄宽)。生物可降解地膜和普通塑料膜厚度均为0.08 mm；土垄为人工木板拍实原土,经风吹雨打形成土壤结皮。土垄、生物可降解地膜垄、普通地膜垄和平作的代表符号分别为SR、BMR、CMR和TP。根据当地种植经验,集雨垄的坡度为40°,高为25 cm,长为10 m,每1小区有4条垄和3条沟。试验于2012—2013年进行,相关种植管理方法按前期研究者[24]所述进行。试验处理编号、垄面积、沟面积和垄覆盖材料见表1,种植示意图见图1。

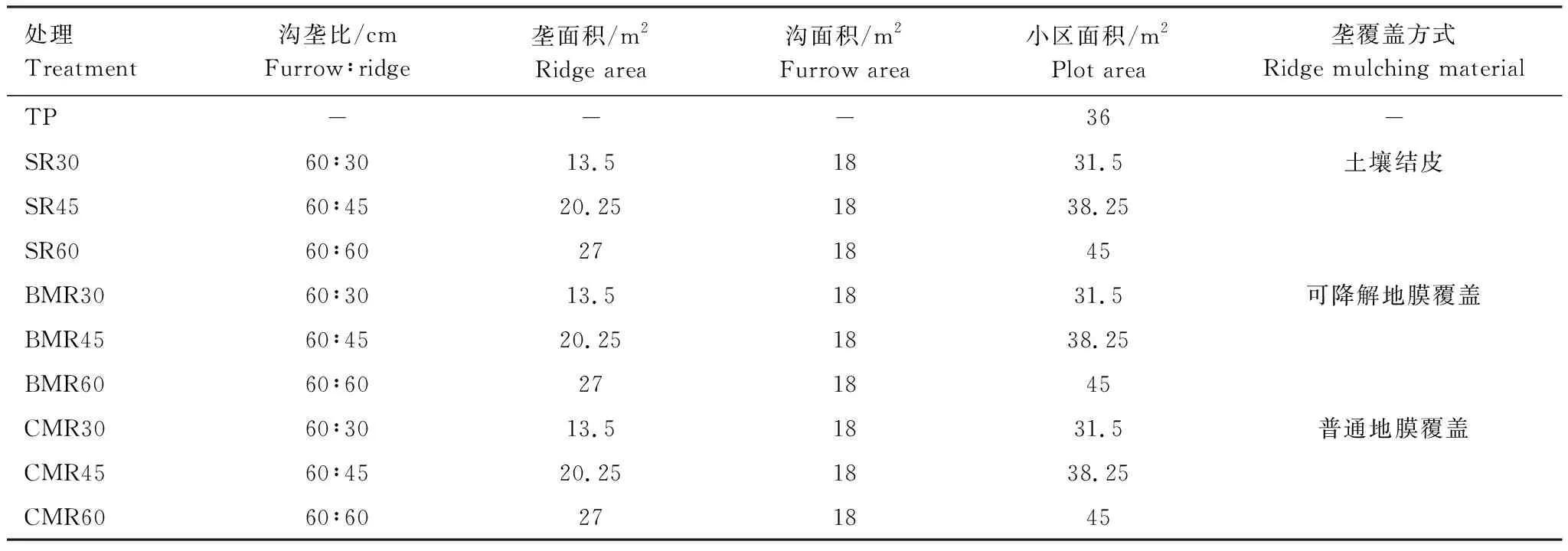
表1 垄沟集雨种植燕麦试验设计

TP: 传统平作 Traditional planting; SR: 土垄 Ridges with manually compacted soil; BMR: 生物可降解膜垄 Ridges mulched with biodegradable mulch film; CMR: 普通地膜垄 Ridges mulched with common plastic film; 侧标30, 45和60表示垄宽

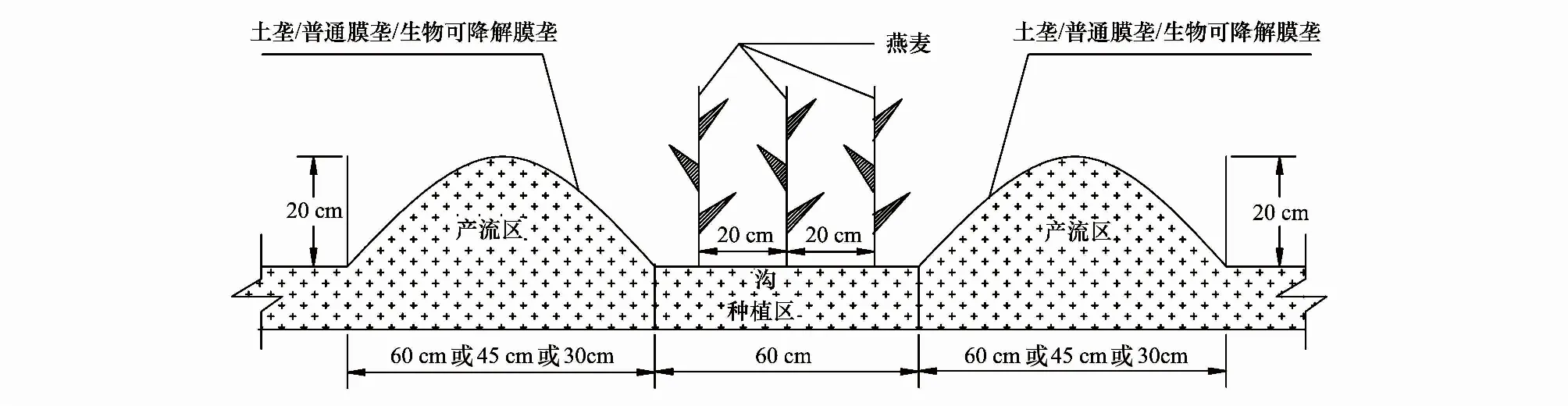
图1 燕麦种植示意图Fig.1 Schematic diagram for oats production in ridge-furrow rainwater harvesting

1.3 Laio土壤水分动态随机模型

土壤水分动态随机模型是以概率的形式来表达土壤水分的动态过程,其理论基础是物质平衡原理：单位时间内土壤含水量的变化等于土壤水分输入项与水分损失项之差[21]。在前人研究[8]的基础上,Laio等[17]通过引进土壤吸湿系数和土壤凋萎系数两个临界土壤含水量,建立了时间尺度为1 d空间一点上的土壤水分平衡方程,具体模型(Laio模型)可表述为：

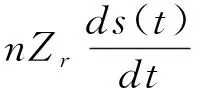
=R(t)-I(t)+Qs(t);t+Es(t)+Ls(t)

(1)

式中,n为土壤孔隙度；s为土壤含水量,以饱和度表示；Zr为根系层深度(cm)；s(t)为t时刻的土壤相对湿度(0≤s(t)≤1),即s(t)=θ(t)/n,其中θ(t)为t时刻的土壤体积含水量(%)；φs(t);t是降水入渗率(cm/d),代表实际到达土壤的降水量部分,即φs(t);t=R(t)-I(t)-Qs(t);t,其中R(t)、I(t)和Qs(t);t分别为降水速率(cm/d)、植物截留率(cm/d)和地表径流率(cm/d)；蒸散发和渗漏构成损失项,即χs(t)=Es(t)+Ls(t),其中Es(t)为蒸散发强度(cm/d),Ls(t)为深层渗漏率(cm/d)。模型忽略土壤水分侧向交换及局地地形条件对土壤水分运移的影响。

由于单次降水量及降水频率具有随机性,且植物冠层截留量受植物类型、叶面积指数、降水强度及降水持续时间等因素的影响,故根据Laio模型假设条件[25],可确定研究时段内降水量在土壤根系层的分布情况及降水量频率输出情况。具体表达式[12, 17]为：

nZr=αγ

(2)

λ′=λe-Δ/α

(3)

式中,α为研究时段内降水量平均值(cm/d)；γ为标准化之后的降水量(d)；Δ为冠层截留阈值(cm)；λ′为降水输出频率(d-1)；λ为降水频率(d-1)。

将降水随机过程同土壤水分损失项(蒸散发与深层渗漏之和)的模拟相结合是土壤水分随机模型建立的基础[26]。Laio模型的蒸散发损失项整合了土壤蒸发与植被蒸腾,并将土壤蒸散发过程分为土壤水分胁迫条件和无水分胁迫条件下的蒸散发[17]。同时,Laio模型假设土壤根系层水分与地下水之间无相互作用,当土壤水分超过田间持水量时,深层渗漏开始变为主导,其大小由饱和水力传导度和土壤含水量决定。

由于降水量为随机变量,公式(1)关于土壤水分的解只能以概率的形式表达土壤水分动态过程。将Laio模型的各土壤水分损失过程转化为Chapman-Kolmogorov前进方程可分析求解导出土壤水分概率密度函数,其具体表达式[17, 25-26]为：

(4)

1.4 数据获取与处理

试验期降雨量数据由中国气象局定西干旱气象与生态环境试验基地自动气象站测定。土壤含水量采用烘干法(105℃,10 h)测定,测定时间为2012—2013年燕麦播种前(4月10日左右)、收获后(8月20日左右)和降雨后(降雨量>5 mm),测定深度140 cm,分层深度为20 cm,共记录7个土层的土壤含水量,每1小区随机在沟内选取3个样点,同1层次3个样点的土样均匀混合。试验期土壤含水量的测定总次数为163次。同期的气象数据由邻近的试验基地气象观测站取得。试验集雨垄(SR、CMR和BMR)径流量由试验期降雨量数据基于美国水土保持局研制的SCS-CN模型反推确定[27-28],TP为传统平作处理,故不进行集雨垄径流量计算。

Laio模型涉及参数通常采用实地测定与查阅相关文献资料确定。本研究实地测定于2013年5—8月份完成。土壤容重采用环刀法测定,测定深度140 cm,分层深度为20 cm,每层3个重复,取均值,并通过计算获得相应土层的土壤孔隙度；根系层深度通过实地调查根系生物量分布范围测定；田间持水量、永久凋萎系数、土壤参数β值及土壤饱和导水率参照文献获得[17, 24]；土壤吸湿系数由永久凋萎系数间接计算确定[29]；植被截留阈值Δ用喷水称重法测定[29],取各生育期均值；由于当土壤含水量高于田间持水量的80%时,作物将不受到水分胁迫[12, 30],故选取田间持水量的80%作为水分胁迫开始点s*；土壤水分达到凋萎含水量及田间持水量时的日平均蒸散发率(Ew和Emax)通过FAO-56提供的作物系数法[12]求得。

通过将烘干法测定的不同土层质量含水量换算为体积含水量,由加权平均法[31]可获得根系层土壤体积含水量。为便于描述,将根系层土壤体积含水量折算为土壤饱和度。相关计算公式如下：

θv=θm×ρ

(5)

θz=15θ20+10θ40+10θ60+10θ80+10θ100+10θ120+10θ140/75

(6)

s=θz/nz

(7)

式中,θv为土壤体积含水量(%)；θm为土壤质量含水量(%)；ρ为土壤容重(g/cm3)；θz为根系层土壤体积含水量(%)；θ20为0—20 cm的土壤体积含水量(%),其余类同；s为土壤饱和度；nz为根系层土壤孔隙度,即各土层土壤孔隙度平均值。

1.5 数据分析与模型验证

利用MATLAB R2014a软件,采用Mann-Kendall非参数检验法[32]对试验区降水趋势进行分析；采用Jarque-Bera检验法[33]对不同处理下燕麦生长季根系层土壤水分含量进行正态性检验；基于SCS-CN模型及其在垄沟集雨系统不同处理下的参数值[27-28],对各试验集雨垄在不同降雨量下的径流量进行模拟；基于Laio模型对不同处理下土壤水分概率密度函数曲线进行数值模拟,并采用局部敏感性分析法[34]对模型参数进行敏感性分析。利用IBM SPSS 15.0软件,采用Duncan新复极差法对根系层土壤含水量在不同处理间及生长季各月份间的差异进行显著性检验(P<0.05)。同时,通过比较研究区各处理实测土壤水分概率密度函数曲线与Laio模型模拟曲线的形状特征(峰值及其位置、90%置信区间)、数字特征(期望、方差)及CM指数[35],验证与评价模型模拟有效性。CM指数越接近1,表明模型模拟值与实测值越接近。

2 结果与分析

2.1 研究区降雨特征及趋势

通过对试验期2 a(2012—2013年)降雨量数据统计分析知,研究区降水量季节分配极不均匀,主要集中在5—10月生长季,分别占全年降水量的83.9%(2012)和87.6%(2013)。在2012年和2013年燕麦全生育期,降雨发生次数分别为77和82次,降雨量分别为380.7 mm和427.6 mm,分别占年降雨量的91.9%和95.3%。2012年,<5 mm降雨为50次,占总降雨次数的64.9%；5—10 mm的降雨13次,占总降雨次数的16.9%；10—20 mm降雨10次,占总降雨次数的13.0%；>20 mm的降雨4次,占总降雨次数的5.2%。2013年,<5 mm降雨为56次,占总降雨次数的68.3%；5—10 mm的降雨12次,占总降雨次数的14.6%；10—20 mm降雨7次,占总降雨次数的8.5%；>20 mm的降雨7次,占总降雨次数的8.5%。同时在连续时间序列上,降水量和降水间隔时间均服从指数分布(图2),且观测值与模拟值的拟合效果较理想(图2a：R2=0.9755,P<0.05；图2b：R2=0.9712,P<0.05),说明试验区降水特征满足Laio模型相关假设条件。

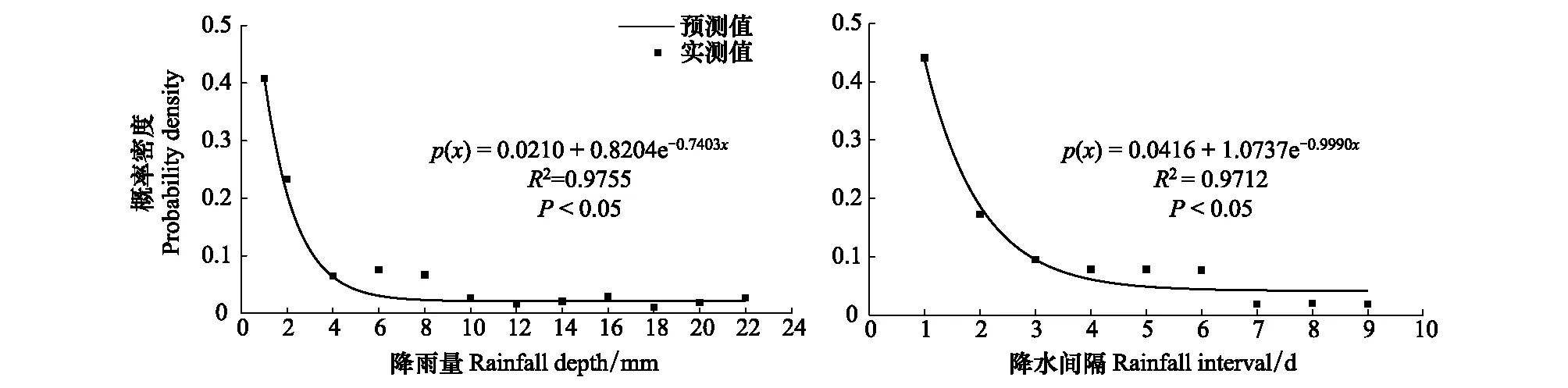
图2 研究区降水量及其间隔时间分布特征Fig.2 Distribution characteristics of rainfall and its interval in the experimental site

采用Mann-Kendall非参数检验法对试验区2000—2015年不同尺度(月、季和年)降水趋势进行分析。由表2可知,在月尺度上,2和9月分别通过置信度90%和95%的显著性检验,且SE均为正值,说明近16年中2和9月降水呈缓慢增长趋势,9月增长趋势最大(1.490 mm/a)；由于6月MKZ值接近90%的判定标准临界值,且SE为正值,故认为6月降水有增加的趋势；除2、6和9月外,其他各月降水量无增加或减少趋势。由表3可知,在季节尺度上,冬季通过了90%的显著性检验,且SE为正值,表明近16年年试验区冬季降水(降雪)呈缓慢增长趋势；春、夏与秋季降水均未通过显著性检验,表明近16年这3个季节降水无增加或减少趋势。在年尺度上,降水量趋势分析通过了90%的显著性检验,且SE为正值,说明近16年试验区降水量呈缓慢增长趋势。

2.2 不同集雨垄径流特征分析

由于Laio模型不考虑单次降水事件的中间过程,只关注来水量对土壤水分的补给,故本研究将单次降水过程中集雨垄径流量作为单次降水的随机事件处理,即模型降水输入量等于试验集雨垄径流量与对应降雨量之和。图3为基于SCS-CN模型的研究区试验期不同降雨量下各试验集雨垄(SR、CMR和BMR)径流量模拟结果。由图3可知,各处理模拟径流量与降雨量之间有较强线性相关性。BMR相关系数R2=0.991,临界产流降雨量为1.35 mm,平均集水效率87.892%；CMR相关系数R2=0.997,临界产流降雨量为0.95 mm,平均集水效率94.203%；SR相关系数R2=0.943,临界产流降雨量为5.31 mm,平均集水效率27.488%；由于TP不涉及垄面产流,故其降水输入量为自然降水量。因此,研究区处理BMR、CMR、SR和TP对应模型降水输入值分别为1.879P-1.189、1.942P-0.899、1.275P-1.460和P(其中P为研究区实际降水量,mm)。由模型输入降水量可确定出研究区生长季平均降水量及生长季降水频率(表5)。

表2 研究区月尺度降水量Mann-Kendall检验值

MKZ: Mann-Kendall检验Z值Zvalue of Mann-Kendall test;SE: Mann-Kendall检验Slope Estimate值 Slope estimate value of Mann-Kendall test; *和**分别表示MK通过置信度90%和95%的显著性检验

表3 研究区年季尺度降水量Mann-Kendall检验值

注: 春季为3—5月, 夏季为6—8月, 秋季为9—11月, 冬季为12—2月

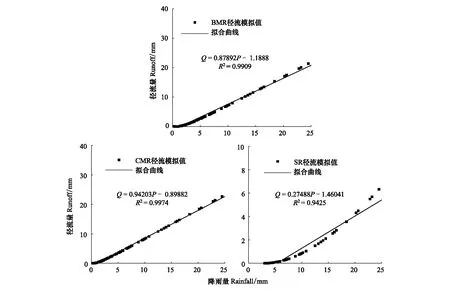
图3 研究区不同处理径流模拟值与降雨量之间关系Fig.3 The relationship between runoff simulation value and rainfall for different treatments in the experimental siteBMR: 生物可降解膜垄 Ridges mulched with biodegradable mulch film; CMR: 普通地膜垄 Ridges mulched with common plastic film; SR: 土垄 Ridges with manually compacted soil

2.3 根系层土壤水分动态分析

图4为研究区2012—2013年不同处理土壤含水率的动态变化。由图4可知,燕麦生长季,不同月份之间土壤水分存在明显差异,不同处理之间也差异明显。4—5月份燕麦植株生长较缓,根系分布较浅,同时降雨量较多且蒸散量较低,各处理土壤含水量处于全生育期最高水平。5—6月份随着降水增多,土壤水分保持在一个较高的水平上,但随着气温继续升高和植物蒸腾及土壤蒸发作用的增强,各处理土壤水分损失逐渐增大,故从5月开始,土壤水分开始逐渐下降。6月份,各处理土壤含水量相对较低。7—8月份燕麦进入生育后期,降雨量较少,气温较高且蒸散量较强,各处理土壤含水量处于全生育期最低水平。同时由于2013年试验期降雨量(427.6 mm)大于2012年(380.7 mm),故各处理土壤含水量2013年均高于2012年同期(除4月份外)。在同一覆盖材料下,不同垄宽对应土壤含水量排序依次为SR60(CMR60/BMR60)> SR45(CMR45/BMR45)> SR30(CMR30/CMR30),各垄宽之间差异不显著。同时,对同一覆盖材料下3种垄宽的土壤含水量求均值发现,在不同覆盖材料下,CMR和BMR的土壤含水量显著大于SR,SR的土壤含水量显著大于TP。

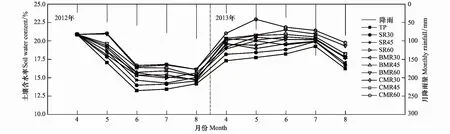
图4 研究区2012—2013年不同处理土壤含水率的动态变化Fig.4 Dynamics of soil water content for different treatments in the experimental site during 2012 and 2013TP: 传统平作 Traditional planting; SR: 土垄 Ridges with manually compacted soil; BMR: 生物可降解膜垄 Ridges mulched with biodegradable mulch film; CMR: 普通地膜垄 Ridges mulched with common plastic film; 侧标30, 45和60表示垄宽

指标IndexTPSR30SR45SR60CMR30CMR45CMR60BMR30BMR45BMR60H0000000000P0.2310.2040.1840.1050.1780.1260.4560.5000.1280.117JBSTAT1.4481.5461.6302.2791.6622.0220.9320.4731.9952.111

H: Jarque-Bera检验测试结果, 若H=0, 则认为样本X服从正态分布; 若H=1, 则认为X不服从正态分布 The returned value ofH=1 indicates that JB test rejects the null hypothesis (the data are normally distributed) at the default 5% significance level, and 0 otherwise;P: 接受假设的概率值, 若P<0.05, 则拒绝原假设, 认为样本X呈非正态分布; 若P>0.05, 则支持原假设, 认为样本X呈正态分布 The returnedP-value less than 0.05 indicate that JB test rejects the null hypothesis (the data are normally distributed), and more than 0.05 otherwise; JBSTAT: 测试统计量的值 The test statistic of JB test

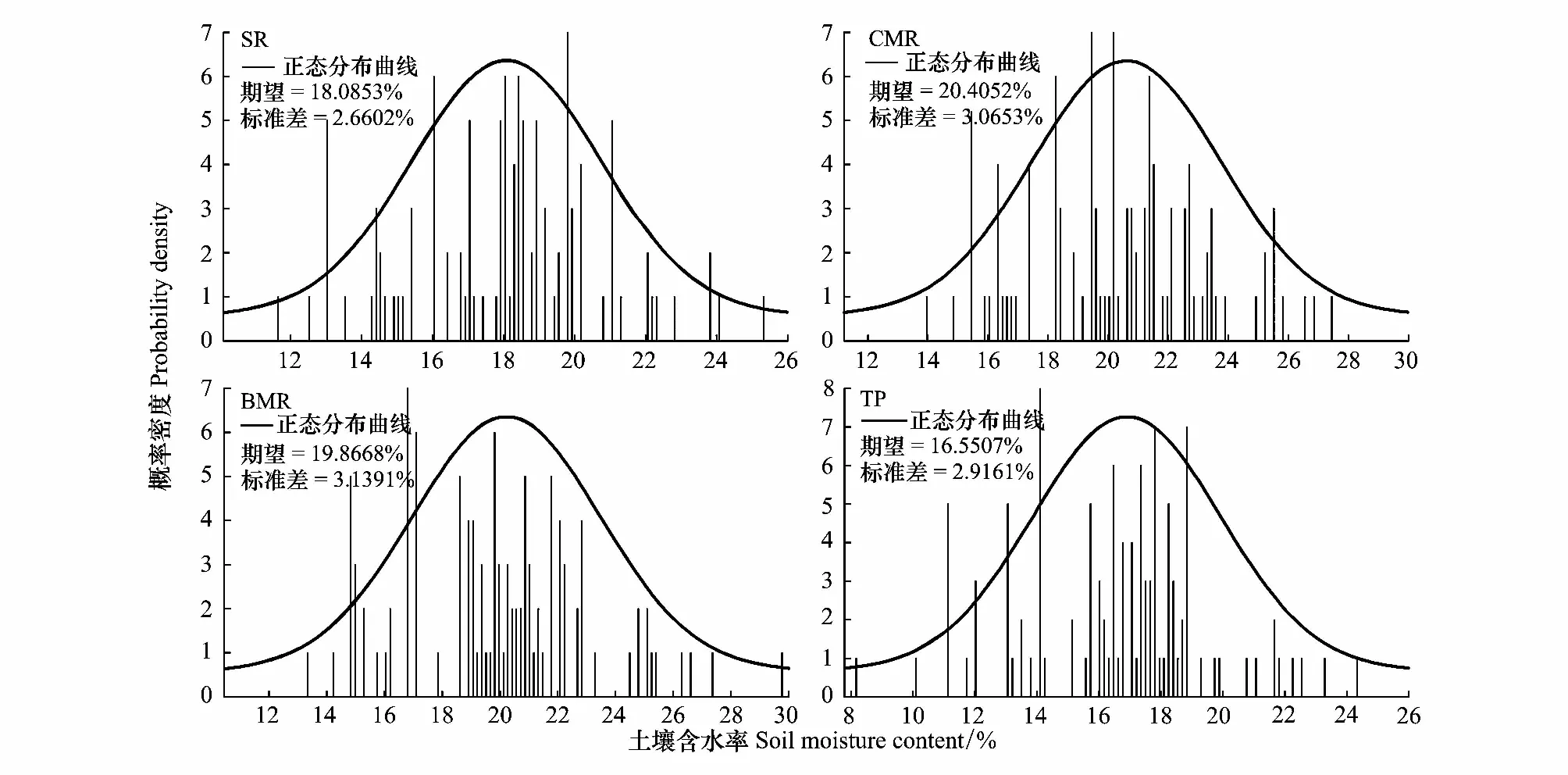
图5 研究区2012—2013年不同处理土壤含水率概率分布特征Fig.5 Probability distribution characteristics of soil water content for different treatments in the experimental site during 2012 and 2013SR: 土垄 Ridges with manually compacted soil; CMR: 普通地膜垄 Ridges mulched with common plastic film; BMR: 生物可降解膜垄 Ridges mulched with biodegradable mulch film; TP: 传统平作 Traditional planting

采用Jarque-Bera检验法对研究区2012—2013年不同处理土壤水分进行正态性检验(表4)。由表4可知,研究区各处理土壤水分Jarque-Bera检验的H值均为0,且P值均大于0.05,说明各处理土壤水分均服从正态分布。通过利用2012—2013年研究区不同覆盖材料集雨垄的平均土壤含水量,借助MATLAB R2014a软件可获得不同处理土壤水分概率分布直方图及正态拟合曲线(图5),由图5可知,各处理土壤水分概率分布直方图均呈单峰状,SR、CMR、BMR和TP对应峰值分别发生在θ=18.065%、θ=20.405%、θ=19.969%和θ=16.551%处,且变化范围分布在区间[17.583%, 18.580%]、[19.826%, 20.984%]、[19.276%, 20.462%]和[15.999%, 17.102%]。同时各处理土壤水分正态拟合曲线对应方差分别为0.708‰、0.939‰、0.985‰和0.408‰(SR、CMR、BMR和TP),说明试验区各处理土壤水分在其均值处分布较集中。

2.4 根系层土壤水分概率密度函数随机模拟

Laio模型共涉及土壤、植被和气候等13个参数,田间垄沟集雨各处理对应模型参数取值通过实地测定与查阅相关文献获取[12,17,24,29-30]。通过野外测量获得不同处理下燕麦平均根系层深度为0—140 cm,土壤平均容重为1.38 g/cm3。由于将集雨垄径流量作为单次降水的随机事件处理,故生长季各处理(SR、CMR和BMR)平均降水量和平均降水频率由试验集雨垄径流量与对应降雨量之和分析求得,TP处理由自然降水量分析得出。Laio模型涉及的其他各参数及其取值见表5所示。

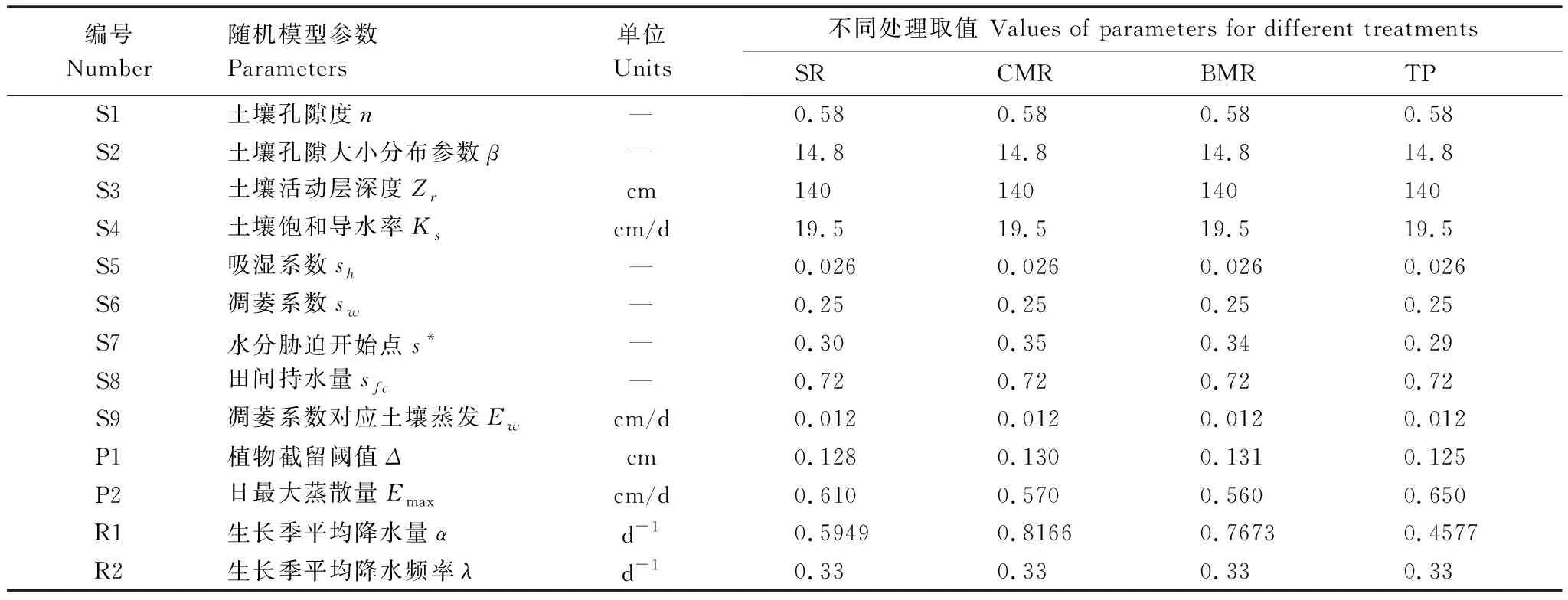
表5 Laio模型参数及其取值

S：土壤参数 Soil parameter；P：植物参数 Plant parameter；R：降雨参数 Rainfall parameter

参数敏感性分析是实现高效便捷地模型优化和参数率定的前提和基础,同时,是模型构建过程中的一个关键环节。本文以研究区SR处理为例,采用局部敏感性分析法对Laio模型参数进行敏感性分析(图6)。由图6a可知,当各参数原值增加10%时,参数λ、α和s*对p(s)峰值有明显影响,且峰值变化幅度均大于60%,其他参数对p(s)峰值均无明显影响。当各参数原值减少10%时,参数sw、Zr、n、Emax、Δ和Ew对p(s)峰值有明显影响,其中sw对应峰值变化幅度大于60%,Zr、n、Emax、Δ和Ew对应峰值变化幅度小于60%,但其他参数对p(s)峰值均影响不明显。由图6b可知,当各参数原值增加或减少10%时,除参数sw和s*对目标变量p(s)对应阔度值影响明显外,其余参数均对p(s)对应阔度值影响不明显。根据Laio模型涉及的13个参数对p(s)峰值和阔度的影响程度,可将其分为2类：第1类为不敏感参数,包括β、sfc、sh和Ks；第2类为敏感参数,包括λ、α、sw、s*、Zr、n、Emax、Δ和Ew。

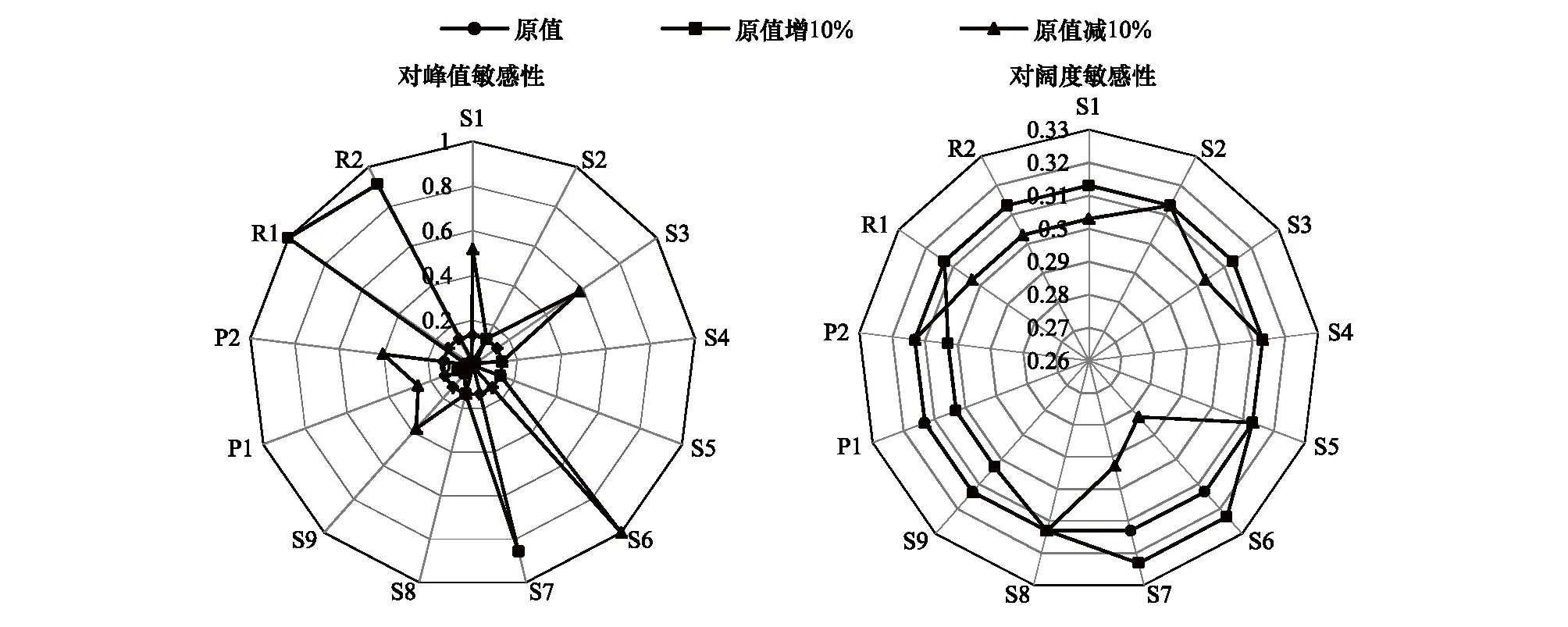
图6 Laio模型参数敏感性分析Fig.6 Sensitivity of parameters in Laio soil moisture dynamic stochastic modelS1为土壤孔隙度; S2为土壤孔隙大小分布参数; S3为土壤活动层深度; S4土壤饱和导水率; S5为吸湿系数; S6为凋萎系数; S7为水分胁迫开始点; S8为田间持水量; S9凋萎系数对应土壤蒸发; P1为植物截留阈值; P2为日最大蒸散量; R1为生长季平均降水量; R2为生长季平均降水频率

为验证Laio模型在研究区的可行性,利用试验期各处理模型参数值(表5),根据Laio土壤水分概率密度函数p(s)表达式(式(4)),得到垄沟集雨系统各处理根系层相对土壤水分概率密度函数(图7)。由图7可知,各处理根系层(0—140 cm)相对土壤水分p(s)均呈单峰曲线,SR、CMR、BMR和TP的峰值分别为6.6638、6.3787、6.4631和7.6410,分别出现在s=0.3131、s=0.3636、s=0.3435和s=0.2829的位置,相应土壤含水量分别为θ=18.160%、θ=21.089%、θ=19.923%和θ=16.408%；峰值的90%置信区间分别为[17.568%, 18.345%]、[20.196%, 21.982%]、[19.227%, 20.590%]和[16.002%, 16.814%]；方差分别为0.606‰、1.060‰、1.075‰和0.692‰；同时膜垄的土壤含水量显著大于土垄,土垄的土壤含水量显著大于平作。

以上分析结果与图5中实测得到的正态曲线峰值及其出现的位置和90%置信区间非常接近,能较好反映土壤水分的概率分布特征。为进一步验证Laio模型模拟与实测p(s)曲线的吻合度,分别对两者的数字特征(期望与方差)和CM指数进行分析比较。与实测值相比,发现SR、CMR、BMR和TP的期望模拟误差分别为0.526%、0.335%、0.220%和0.864%；方差模拟误差分别为7.481%、6.203%、4.460%和9.773%；CM指数分别为0.523、0.824、0.683和0.518；期望与方差模拟误差均在允许误差范围,CM指数均大于0.5。说明Laio模型可对研究区垄沟集雨系统燕麦根系层土壤水分概率密度函数进行较好地预测。

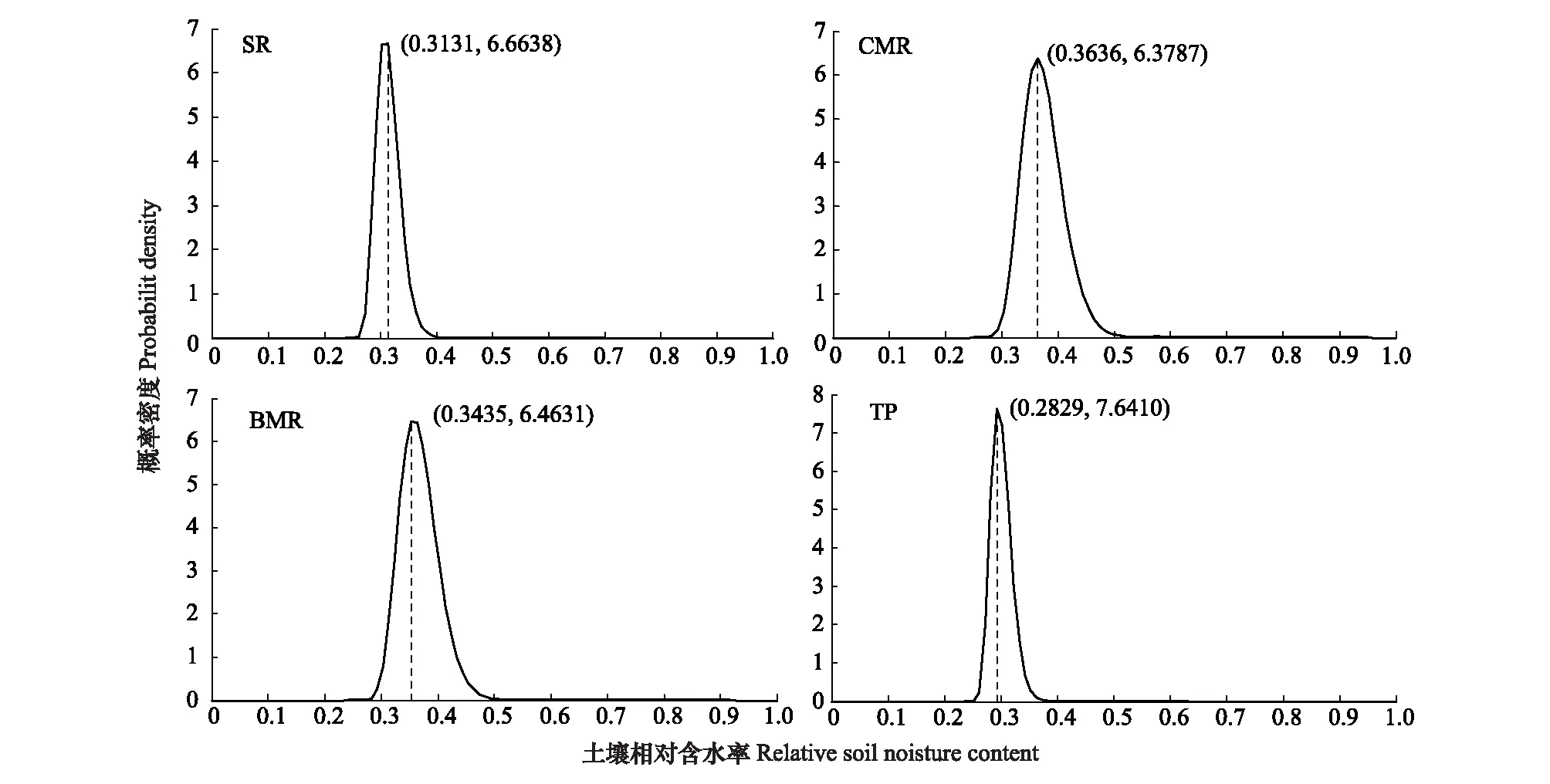
图7 研究区2012—2013年不同处理相对土壤水分的概率密度函数模拟结果Fig.7 Probability density function of soil water content for different treatments in the experimental site during 2012 and 2013SR: 土垄 Ridges with manually compacted soil; BMR: 生物可降解膜垄 Ridges mulched with biodegradable mulch film; CMR: 普通地膜垄 Ridges mulched with common plastic film; TP: 传统平作 Traditional planting

3 讨论

研究区地处黄土高原西部边缘半干旱地带非灌溉区,地下水补给微弱,天然降水是生长季土壤水分的唯一来源,故降水格局对该区域土壤水分状况的影响较大。从降雨量分布来看,试验区降雨事件主要以0—5 mm为主(占总降雨次数的66.6%),在多数情形下,这种降水格局使得降雨量无法满足植物生长需求,是该研究区比较干旱的主要原因[36]。从降雨总量而言,85.32%的年降雨量来源于>10 mm的降雨,且主要集中在7—8月生长季,以暴雨为主；这种降水特征使该研究区具有明显的干湿两季,湿季较短,干季较长。从降雨趋势来看,近16年(2000—2015)试验区降水量呈缓慢增长趋势；霍正文等[37]以研究区54年降水资料分析发现,2003年以后研究区降雨量存在不显著增加趋势,这与本文研究结果相类似。同时,从生长季根系层土壤水分及降水量季节变化可知,随降水量年内年际间的变化,垄沟种植各处理土壤含水量均呈显著变化,但土壤含水量与降水量未呈现显著相关关系。这是由于土壤水分动态对降水事件响应是1个非常复杂的过程,该过程不仅受降雨事件大小的影响,而且受到降水强度、干旱期长短、植被类型和土壤质地等的影响[38]。

垄沟集雨种植建立的垄沟产流、集水、蓄墒系统,能够使无效降水形成径流叠加到种植沟内,促进降水下渗,抑制无效蒸发,改善土壤水分生态环境,同时能够提高土壤抗冲抗蚀力,减少水土流失,增加作物生物量及产量[7, 36, 39]。王琦等[40]对垄沟集雨系统集水效率研究发现,膜垄和土垄的平均集水效率分别为91.1%—94.3%和24.6%—28.8%,同时土垄径流产生主要由高强度暴雨引起,膜垄径流损失主要由降雨过程中集水面截留和蒸发损失引起。任小龙等[41]研究指出,垄沟覆膜系统能使<5 mm的无效降水转化为有效水分贮存于土壤中,平均集水效率达到了90%。李小雁等[42]研究发现,CMR和SR的平均径流效率分别为87%和7%,且SR的径流效率随着降雨量和降雨强度的增加而增加。与上述结论一致,本研究发现BMR、CMR和SR临界产流降雨量分别为1.35、0.95 mm和5.31 mm,平均集水效率分别为87.892%、94.203%和27.488%。说明BMR、CMR对降雨资源利用效率显著高于SR,且能够显著改善干旱区作物根系层土壤水分供应状况,提高作物水分利用效率和产量。

土壤水分动态随机模型的核心是土壤水分概率密度函数,是以概率的形式表达土壤水分的动态过程,即是将土壤水分看作一个受降雨、蒸散发、渗漏等多个因素影响的随机变量,通过分析降雨、入渗、蒸散发、径流、渗漏等过程,结合土壤水分平衡方程来研究土壤水分动态的统计特性与大气、土壤和植被的生态水文学关系[17, 21,26]。由于Laio模型广泛应用于仅有降水输入,无地下水补给的干旱半干旱地区[12],垄沟集雨系统在降水输入的过程中伴随垄面径流的输入,故Laio模型在该系统的应用受到了限制。然而垄沟集雨系统垄面径流的产生受制于降水的发生,于是本研究将单次降水过程中垄面径流量作为单次降水的随机事件处理,利用Laio模型对该系统燕麦生长季土壤水分概率密度函数p(s)进行模拟,发现该系统各处理p(s)曲线的峰值较大(CMR/BMR小于SR/TP),峰的阔度较窄(CMR/BMR大于SR/TP),且峰值出现点靠近土壤水分胁迫开始点。这与Laio等[17]通过对不同降水特征、土壤类型及植被盖度等条件下p(s)曲线的分布特征分析结论基本一致。表明Laio模型仍然适用于该系统。本文仅对Laio 模型在该系统作物生长季土壤水分动态随机模拟应用方面做了初步的探讨,针对不同作物类型及生育期、不同土壤类型及土层等因素对该系统水文与生态过程的影响机制需后续进一步研究。

建立土壤水分动态理论模型的验证、参数率定和敏感性分析的方法体系是生态水文学研究的关键[26]。Laio模型共涉及土壤、植被和气候3方面的13个参数,为确保模型模拟结果的可靠性,对模型涉及参数敏感性进行分析是必要的。Miller等[31]研究发现Laio模型中参数Emax和s*的敏感性较高。姚淑霞等[25]通过借鉴Teuling等和Miller等敏感性分析法,将Laio模型13个参数划分为弱、中等和强敏感性3类,其分类结果与本文利用局部敏感性分析法得到结果基本一致。由于Laio模型的参数涉及土壤、植被和气候等诸多因素,不同的研究区对应模型参数的敏感性也存在差异,同时,局部敏感性分析法忽略参数间交互作用对模型结果的间接影响,敏感性分析结果具有一定的片面性。故在后续研究中需考虑模型参数之间的相互关联性,利用全局敏感性分析法识别模型输出响应的重要影响参数,为建立有效的参数率定和敏感性分析方法体系提供条件。

4 结论

研究区2012—2013年降水量季节分配极不均匀,主要集中在5—10月份生长季；降雨事件主要以0—5 mm为主,占总降雨次数的66.6%；年降雨量的85.32%来源于>10 mm的降雨,且以暴雨为主；近16年(2000—2015)研究区降水量呈缓慢增长趋势；研究区垄沟集雨燕麦生长季,BMR和CMR的临界产流降雨量、平均集水效率和土壤含水量均显著大于SR,且SR的土壤含水量显著大于TP,各处理土壤含水量序列均服从正态分布(H=0,且P>0.05),概率分布直方图均呈单峰状；通过对Laio土壤随机概率密度函数曲线形状、土壤含水量的数字特征和CM指数等多方面的对比分析,发现该模型能够对垄沟集雨系统各处理土壤水分概率密度函数进行较好模拟,可将试验集雨垄径流量作为单次降水的随机事件处理。