基于动态水力平衡的集中供热系统二次管网节能优化调节方法研究

周璇，刘国强，王晓佩，闫军威

(1.华南理工大学 机械与汽车工程学院，广东 广州，510640；2.广州远正智能科技股份有限公司，广东 广州，510000)

集中供热系统是我国北方城市建筑用能大户，占建筑总能耗的40%～60%，与相似气候条件下的发达国家相比，我国集中供热系统单位建筑面积能耗高 3倍[1]，集中供热系统的节能优化运行是北方供热建筑节能工作重点。集中供热系统二次管网输配系统节能优化调节方式大多采用量调节方法[2]，但由于二次管网各支路之间相互耦合、流量相互干扰，量调节容易造成管网水力失衡、室内供热温度与需求温度偏差较大，导致系统能源浪费或难以满足最不利房间供热需求等现象，因此，本文作者拟在满足动态水力平衡前提下，研究集中供热系统二次管网输配系统的节能优化调节方法。动态水力平衡是二次管网实现节能优化控制的前提和难点。二次管网设计时大多采用成本较高的动态水力平衡阀[3-6]，而对已投入运行的管网常通过循环泵和电动调节阀的优化调节来减少水力失衡度。2013年，DAI等[7]提出在暖通空调水系统中合理地安装水力平衡阀，并采用正确的方法进行系统联调，使系统接近或达到水力平衡；LU[8]以安装有流量控制阀的流体网络为研究对象，利用线性规划、流量控制阀与变频调速综合技术，提高了水力平衡度。2014年，盛超[9]针对管网在部分负荷下末端设备流量分配不均现象，提出了一种新的压降比例控制法，在部分负荷下使各末端的流量分配都得到明显改善。李玉衔[10]提出了基于能量分配平衡的动态水力平衡控制理念，实现各个环路能量分配的动态平衡，有效提高了暖通空调系统的舒适性和运行的经济性。但目前，在二次管网已完成静态水力平衡初调节的前提下，对于如何实现动态水力平衡条件下输配系统节能优化调节的研究尚不多见。本文作者利用电网图论建立二次管网的复杂多元非线性水力工况模型，并利用半经验模型和实测数据建立其输配系统运行能耗模型；在上述模型基础上，以输配系统运行能耗最小为目标，以二次管网动态水力平衡为约束条件，建立基于遗传算法的二次管网输配系统的节能优化调节模型，动态优化输配系统主要能耗设备热水循环泵的运行频率和各末端电动调节阀开度，以实现基于动态水力平衡的二次管网输配系统节能优化调节。

1 二次管网动态水力平衡调节必要性

集中供热系统二次管网中，供热建筑室内温度一般采用单回路控制，仅建立室内供热负荷及其对应支路流量之间的关系。然而，供热管网各支路间具有水力耦合特性，每一支路调节阀发生动作时，对其他支路即整个管网系统的水力工况都有影响，可能使调节阀频繁动作，管网水系统的平衡状态随之变化，导致系统发生震荡，同时会引起运行能耗增加[11]。

图1所示为典型的集中供热系统换热站-建筑物的结构简图。换热站为多栋建筑物供热，且二次管网供热末端不可单独调节，仅通过调节热水循环泵运行频率和进入建筑的各电动调节阀开度实现对各建筑物的供热量调节。在二次管网总流量保持不变的情况下，若同时调节热水循环泵和各个支路电动调节阀开度(即改变管网总阻抗)，其运行工况有无数个组合，如图2所示。图2中：H为管网总阻力，即循环泵扬程，m；G为管网总流量，m3/h；S为管网总阻抗，(kPa·h2)/m3；f为循环泵运行频率，Hz。工况1～5都可实现总流量保持不变，若未考虑循环泵效率，因工况5的管阻最小，无疑其运行能耗最小。然而，若考虑循环泵运行效率，因循环泵在工况5的运行效率低导致增加的运行能耗大于工况4条件下由于管阻增加产生的运行能耗，则工况5的运行能耗反而大于工况4的运行能耗。

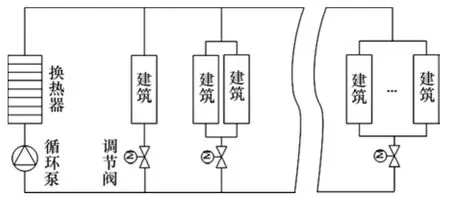
图1 集中供热系统结构简图Fig.1 Structure diagram of central heating system

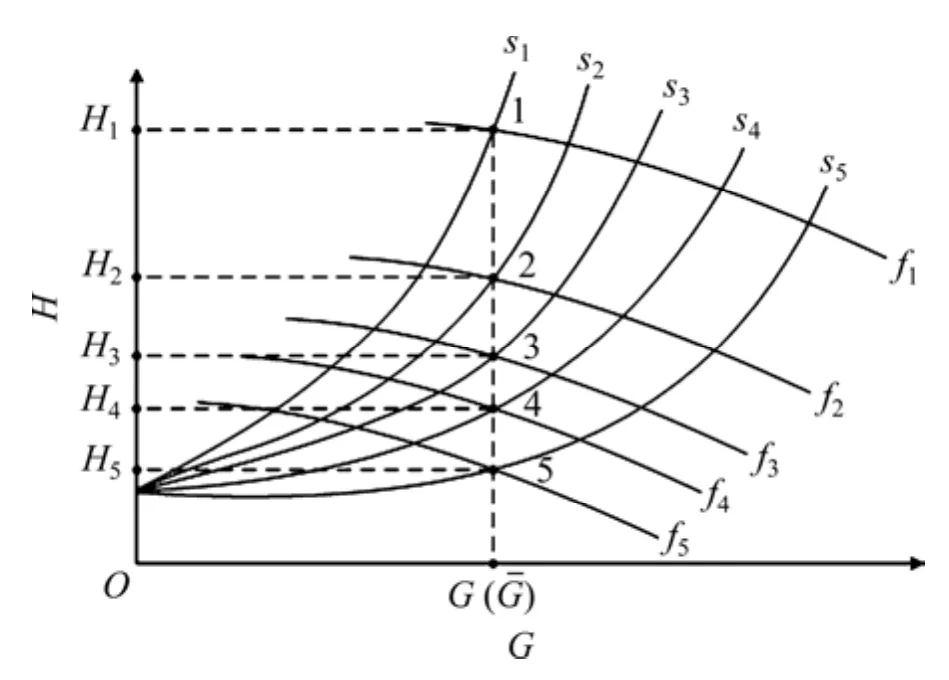
图2 同一流量下多执行机构二次管网的运行工况点组合Fig.2 Combination of operation point of the secondary piping network with multiple actuators under the same flow rate

因此，对于每一个多执行机构二次管网总流量，必定对应1个最佳的循环泵运行频率和管网总阻抗，使循环泵的运行能耗最小。各支路流量由该时刻供热负荷确定，此时，二次管网总流量是由总供热负荷决定。本文的研究目的是：在保证各末端用户的水力稳定性前提下，使系统的运行能耗最小，即当某一栋建筑物(支路)或某几栋建筑物(支路)室内供热负荷发生变化(流量需求发生变化)时，以热水循环泵能耗最小为目标，以满足二次管网水力稳定性和各支路热负荷需求为约束条件，实时优化循环泵运行频率和各支路电动调节阀开度设定值，寻找其最优组合工作点。

2 基于电网图论的水力工况建模

管网水力工况建模是研究动态水力平衡的前提。本文拟以伯努利方程和连续性方程为基础，利用基尔霍夫定理和图论原理，建立管网回路压力平衡方程，以表征管网水力工况变化规律。

2.1 图论基本定义

图3所示为二次管网有向图。图3中，二次管网图Gr可以通过Gr=(V,E,φ)来表示；V表示图Gr的边集合，V=｛v1,v2,…,vm｝；E表示图Gr的点集合，E=｛e1,e2,…,en｝；φ为从E到V的无序或有序配对组合的集合，表示边和节点之间的关联关系。二次管网的每条边都有确定的流向，如图3所示，e1=(v3,v6)成立，而e1=(v6,v3)不成立，称为有向图。

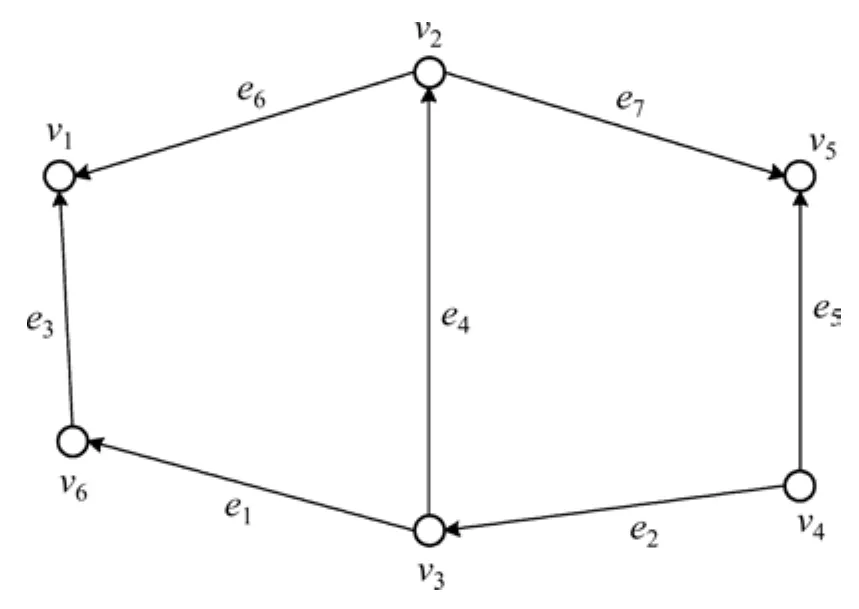
图3 二次管网有向图Fig.3 Directed graph of the second piping network

2.2 水力管网图的矩阵表达

当管网很复杂时，图表示具有局限性。为了借助计算机对管网进行复杂计算，需要把图中的所有元素以代数的方法表示出来，矩阵形式最为便捷。

1) 关联矩阵。若管网有m条边和n个节点，各边和分支间的关联关系可用1个n×m阶的矩阵A(Gr)=aij表示。

2) 基本回路矩阵。在管网图中若有p个基本回路，预先规定基本回路的方向，各边与基本回路间的关系构成p×m阶的基本回路矩阵B(Gr)=bij：

3) 回路压力平衡方程。根据能量守恒原理，密闭管网稳态下，在任意回路中沿回路规定方向或反向，各条边的压降代数恒为零。对某一回路i，有

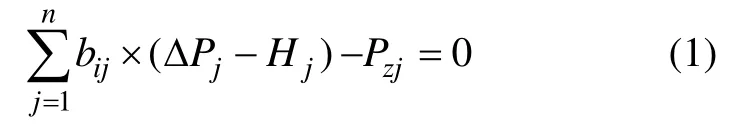
式中：bij为边流动方向；ΔPj为边j的阻力损失，沿流动方向降低为正，反之为负；Hj为边j的输入动力，如泵或风机的动力压头；Pzj为回路i上由重力作用形成的流动动力，一般忽略。

2.3 管网水力工况建模

二次管网一般由3种基本元件连接而成：阀门、管段和循环泵。建立水管网力模型的基础是首先建立管网基本元件的单元压降模型，再利用电网图论建模。

1) 调节阀是通过改变其局部阻力以达到节流目的元件，对于不可压缩流体，由能量守恒原理，可得调节阀的前后压降计算公式：

式中：Δpv为调节阀前后压降；ρ为流体介质密度；S′为阀体流通面积；ξ为调节阀阻力系数；Gv为流过调节阀的流量。

由于调节阀阻力系数ξ与流通面积S′相关，令，则式(2)可改写成

2) 设流体从管段横截面1向横截面2流动，根据伯努利方程，可得

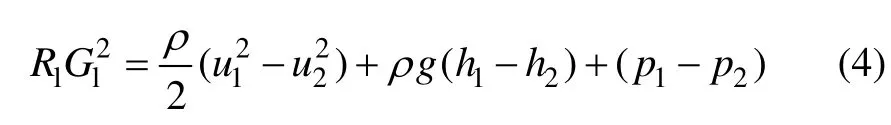
式中：Rl为管段阻力系数；Gl为流过管段的流量；u1和u2分别为管段截面1和2处的流速；h1和h2分别为管段截面1和2处相对地面的高度；p1和p2分别为管段截面1和2处的流体静压。

则管段压降计算公式为

3) 循环泵在管网中一般提供动力压头，其压降方向与流动方向相反，即 Δpp=-ΔHp。

管网回路一般由以上3种单元构成，且对于密闭管网G=Gv=Gl，即综合单元压降为

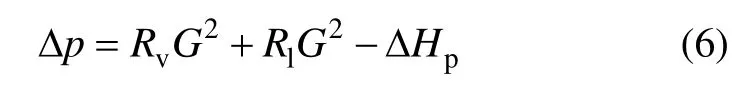
对于多单元回路，根据回路压力平衡方程，得

式中：B为基本回路矩阵，n×m阶；G为回路流量矩阵，为调节阀阻力系数，为管段阻力系数，为循环泵压头，。

3 基于水力工况的热水循环泵建模

利用半经验公式[12]，拟合循环泵的效率模型和扬程模型：

式中：c0，c1和c2为循环泵扬程模型参数，需辨识；d0，d1和d2为循环泵效率模型参数，需辨识；kf为循环泵实际运行频率f与额定运行频率f0(50 Hz)的比值，kf=f/ 50；kG为循环泵实际流量Gp与额定流量G0的比值，kG=Gp/G0；Hp为循环泵扬程，m；η为循环泵运行效率，%，Wp为循环泵总实际运行功率，kW。

采用图解法或数值解法来确定循环泵的性能参数，准确性差，且非常繁琐。最小二乘法是一种使用最为广泛的模型参数辨识方法，这是一种使用最为广泛的模型参数辨识方法，具有运算速度快、收敛可靠、编程简单等特点。因此，本文拟采用最小二乘法对循环泵扬程模型参数进行辨识。

4 基于动态水力平衡的节能优化模型

动态水力平衡的优化目标是在满足各支路水力平衡的前提下，使热水循环泵的运行能耗最低，因此，该优化问题的目标函数及其约束条件可表示为

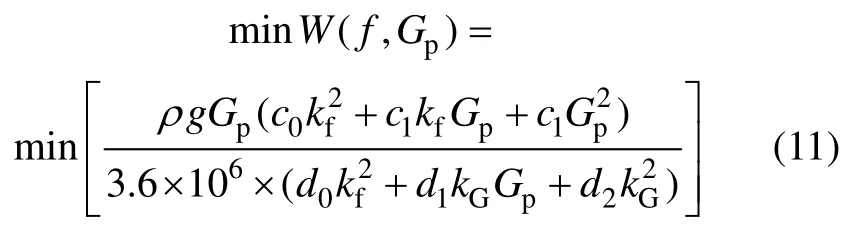
上述模型的约束条件较为复杂，主要包括二次管网各支路的水力平衡度约束、热水循环泵运行频率约束及各支路电动调节阀开度约束3个部分，需针对具体对象进行说明。

处理约束优化问题的主要方法有丢弃法、修理法、修改遗产算子法和惩罚函数，为提高计算效率，本文拟利用惩罚函数法，通过引进惩罚因子把约束问题连接到目标函数中，从而将有约束的最优化问题转化为无约束的最优化问题进行求解[13]。

4.1 优化参数的选取

根据二次管网的运行特征，影响二次管网运行能耗的直接可调变量为循环泵运行频率f和各支路电动调节阀开度φv,i。若各支路的所需流量已知，存在确定的循环泵运行频率f和各支路电动调节阀开度φv,i，使各支路流量保持需求值的同时循环泵的运行能耗最小，达到相应的节能效果。因此，动态水力平衡的运行优化问题可表示为二次管网运行中的循环泵运行频率f和各支路电动调节阀开度φv,i寻优过程。

本文研究方法的前提是二次管网各支路的建筑供热负荷需求已知，在各个控制周期根据各种外界参数实时计算出各支路负荷需求，然后利用寻优算法求出循环泵运行频率和各支路电动调节阀开度优化设定值，将各优化设定值传送给循环泵变频器和电动调节阀执行器进行控制。

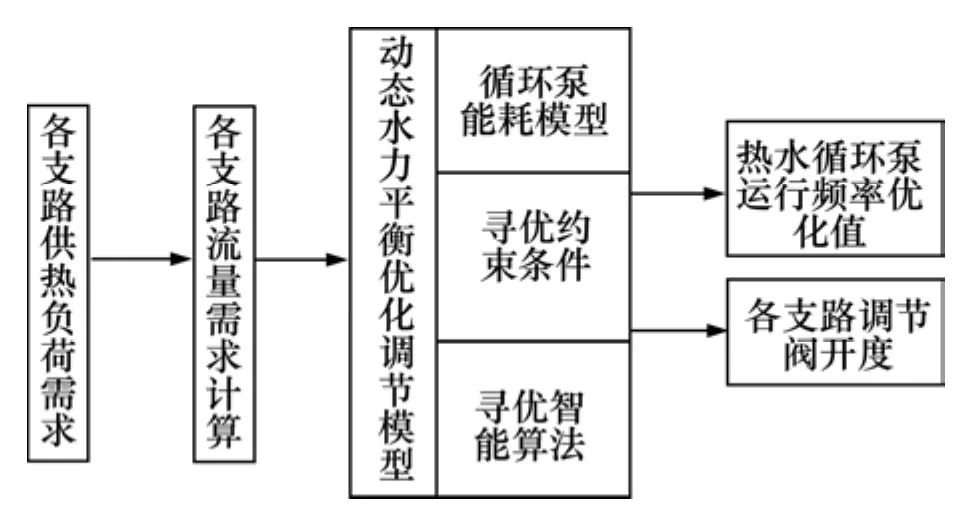
图4 二次网动态水力平衡参数优化调节示意图Fig.4 Diagram of optimization and adjustment on dynamic hydraulic balance parameters of the second piping network

4.2 约束条件的确定

动态水力平衡优化调节模型约束条件主要包括二次管网各支路水力平衡度约束、热水循环泵运行频率约束及各支路电动调节阀开度约束3个部分。

1) 支路水力平衡度约束。各支路的流量需求可以通过供热负荷预测模型计算得到。各支路流量的合理性是室内供热负荷稳定在需求范围内的保障，采用精确的供热负荷模型及对室内供热负荷进行预测分析才能确定下一时刻所需流量，精确的供热负荷模型与太阳辐射、室内人员密度、风速等各类因素相关，建模难度极大。本文仅从设计角度，通过对室外温度的实时采集计算出当前所需流量，支路供热负荷计算公式如式(12)所示，随室外环境温度tw与各支路室内实时需求温度tns,i动态变化。

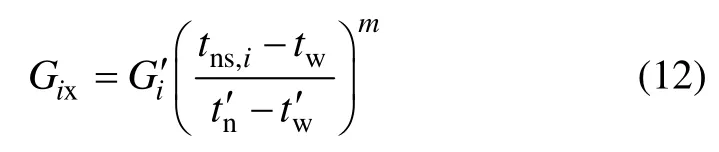
式中：Gix为支路i需求流量，m3/h；Gi′为支路i设计流量，为各建筑设计流量和，m3/h；tns,i为支路i室内需求温度，℃；tw为室外实际温度，℃；tw′为设计室外温度，℃；tn′为设计室内温度，℃；m为流量优化调节系数。

本文根据各支路当前所需流量迭代计算出热水循环泵运行频率和各支路调节阀开度最优组合，求解最优组合的前提是各支路流量满足需求值，将各支路水力平衡度作为约束条件，如下式所示：

式中：Gis为支路i实际流量，m3/h。

2) 热水循环泵运行频率约束。集中供热系统二次管网运行过程中，热水循环泵是二次管网输配系统的主要能耗设备，为各建筑内散热末端输送热水，从而实现热量由换热站到供热用户的传输。热水循环泵运行的约束主要考虑到设备安全运行以及供热用户热水流量和扬程的约束。

一方面，供热系统运行状态不同于供冷系统，在寒冷地区为防止因室外天气骤降导致二次管网管道或散热器冻裂，在整个供热季供热系统不能停止运行，如在寒冷地区140多d内换热站一直运行，因此，尽管有备用泵，每台热水循环泵的运行时间仍较长，若长期处于高速运转，维护成本高，一般不让热水循环泵处于最高速运行状态；另一方面，热水循环泵还必须满足管路特性要求，应保证能为最不利供热用户提供足够的流量和扬程。

二次管网的量调节主要通过热水循环泵的运行频率来调节，因此，将上述约束转化为对热水循环泵运行频率的约束，如下式所示：

式中：fmin为热水循环泵运行频率下限；fmax为热水循环泵运行频率上限。

3) 支路电动调节阀开度约束。各支路电动调节阀开度是调节各支路水力及热力平衡的重要状态参数，因各支路建筑功能和特征不一样，如供热需求温度和时间、墙体材料、室内设备等，因此，每一支路的室内温度变化不一样，当室内供热负荷变化时，调节电动调节阀开度以改变各支路流量，从而改变供热负荷。但是在调节过程中，若调节方式不合理，则可能导致调节阀完全关闭，而此时热水循环泵仍在运行，使换热站侧二次管网管路压力剧增，当超过安全阀值时，泄压阀自动打开排水泄压。为防止此现象的发生，转化为对各支路电动调节阀开度的约束，如下式所示：

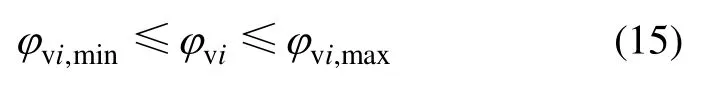
式中：φvi,min为电动调节阀开度下限；φvi,max为电动调节阀开度上限。

4.3 优化算法的选择

根据上述建立的优化模型可以看到，模型优化过程涉及室外温度、支路建筑物室内需求温度、支路流量、支路电动调节阀开度、热水循环泵运行频率及热水循环泵运行能耗等众多参数，是一种多变量的非线性优化问题，各参数有时还具有较大的数量级差，这些都增加了优化求解过程的难度。

此外，从工程应用的实际情况出发，动态水力平衡的运行优化还要求优化方法具有可靠性、快速性、通用性和可控性等，即保证求出最优解的同时，还要求在保证较高精度前提下，求解时间尽可能短。

目前，工程优化问题求解中，常用的优化算法有解析法、网格搜索法、改进Powell方法和人工智能方法等几种。其中解析法、网格搜索法虽具有简单、快速等优点，但其只能得到优化解的大概位置，且容易受到初始条件、速度模型等因素的影响，难以掌握[14]；改进Powell法的优化求解大多采用基于迭代原理的数值解法，这些数值解法通常容易陷入局部最优，难以找到全局最优解，且需要对求解函数性质作诸多限制。而遗传算法作为一种高度并行的随机自适应搜索算法，能够在解空间的多个区域内进行搜索，能以较大的概率跳出局部最优，在解决此类问题时具有独特的优越性[15-16]。

因此，本文综合考虑动态水力平衡优化的特点和难点，并结合优化速度、精度要求以及技术的可实现性，采用遗传算法对动态水力平衡参数优化问题进行求解，并通过罚函数法将具体的优化问题转化为无约束的非线性问题，加快优化求解的速度。

遗传算法(genetic algorithm，简称GA算法)起源于利用计算机进行生物遗传进化模拟技术，是一种基于自然选择原理和基因遗传机制的优化算法，适用于人工复杂非线性和多维空间问题的优化求解。遗传算法的整个工作原理如图5所示。

图5 遗传算法的基本流程Fig.5 Basic flow of genetic algorithm

5 案例分析

5.1 研究对象

本文以某高校换热站二次管网为研究对象，共 3个支路，每条支路流量通过相应的电动调节阀开度进行调节，该二次管网的初调节已完成，初调节后管网手动阀开度不再调节，仅调节二次侧回水管电动调节阀，可把每条支路等价为阻抗不变的大型供热末端，回水管电动调节阀可作为该大型供热末端的流量调节阀。目前循环泵采用变压差变流量运行方式[17]调节循环泵运行频率，根据室外天气变化动态设定二次管网总管的压差，压差随室外天气实时变化。该换热站使用2台板式换热器和2台热水循环泵，其管网结构见图6。

图6 某换热站简化结构图Fig.6 Structure diagram of a heat exchange station

该换热站中，支路 1管径 DN125，供热面积为12 252 m2；支路2管径DN300，供热面积为72 442 m2；支路3管径DN350，供热面积为87 815 m2；各支路电动调节阀口径与管径匹配。

5.2 水力工况建模

简化图6构造如图7所示管网图，共有4个节点，6条边，可选出3个基本回路Ⅰ，Ⅱ和Ⅲ。

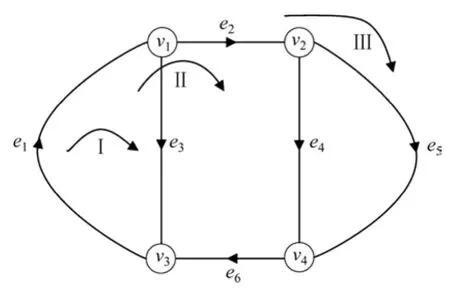
图7 换热站管网图Fig.7 Network diagram of a heat exchange station

由图7，其基本回路矩阵B可写成

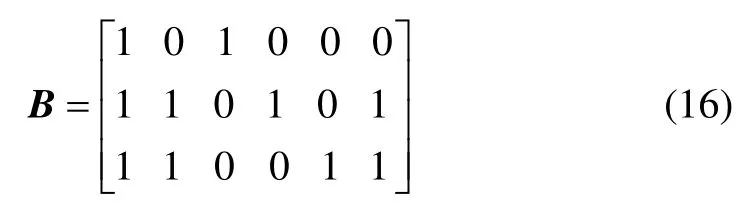
根据式(2)，(7)和(16)可分别建立3个基本回路Ⅰ，Ⅱ和Ⅲ的压降平衡方程：

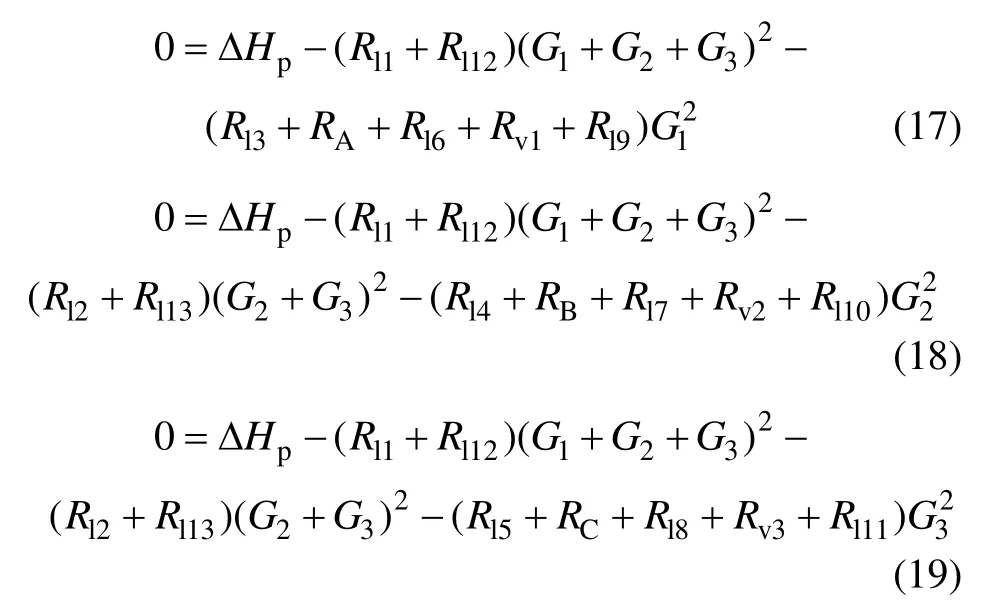
而对于循环泵扬程可采用下式表示[12]：

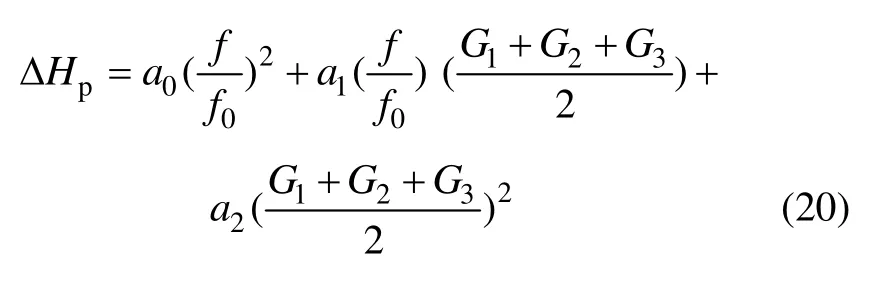
式中：a0，a1和a2为循环泵扬程模型参数，需辨识；f和f0分别为实际运行频率和额定运行频率，Hz。

而对于电动调节阀，其阻力系数与调节阀的本身结构和开度相关，只能通过实验获得阻力系数与开度关系：不断调节开度，测量支路流量和调节阀前后压差，本文所用西门子电动调节阀为等百分比理想流量特性，阻力系数逼近对数形式，测得表达式如下：

式中：b0,i，b1,i和b2,i为支路i电动调节阀模型参数，需辨识；φv,i为支路i电动调节阀的相对开度，%。

如式(18)～(20)所示，支路i流量Gi与循环泵运行频率f和各支路调节阀开度φv,i均相关，但是求解形式十分复杂，为典型的多元非线性求解问题。

式中：G为回路流量矩阵，为回归模型待辨识参数矩阵，4；U为可控变量矩阵，。

为让调节阀开度处于较大变化范围，分别选择室外温度变化范围相对较大的2个工作日即2016-12-27和2016-12-28所采集数据(存储周期为5 min，每日共288组数据)分为模型训练集和验证集，利用matlab和训练集数据辨识模型参数，其中调节阀开度值按原始值输入，如78.5%采集数据为78.5，辨识时也输入78.5，而不是0.785。辨识结果如下：

表征线性回归程度的R2分别为0.893 8，0.767 0和0.918 6，说明线性相关性较好。

将所辨识的参数矩阵代入式(22)，利用2016-12-28数据作为验证。2016-12-28供热系统输入量(调节阀开度和循环泵运行频率)变化曲线见图8和图9，各支路流量计算值和实测值对比变化曲线见图10～12。

由图10～12可知：支路流量模型计算值和实测值变化曲线具有较高的吻合性，各支路流量最大相对误差在±8%以内，基本符合水力平衡流量偏差在±10%以内的要求[19]，能满足本文对动态水力平衡优化调节的仿真研究。

5.3 热水循环泵能耗建模

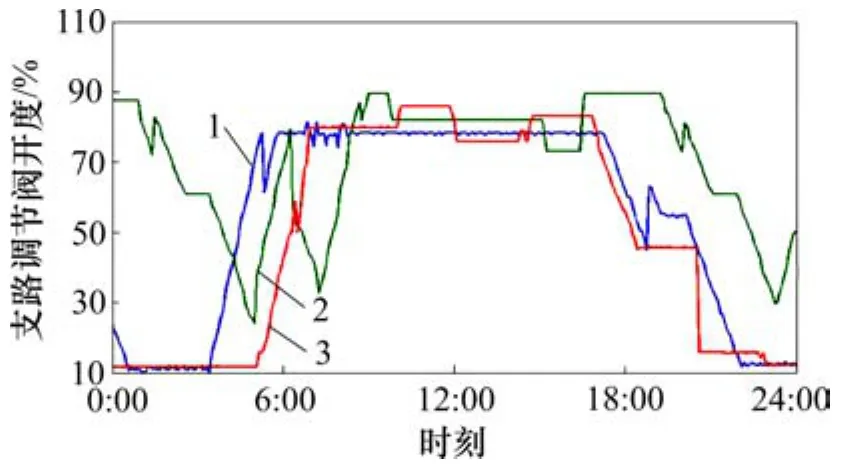
图8 支路调节阀开度变化曲线Fig.8 Varying curve of branch valve on openness

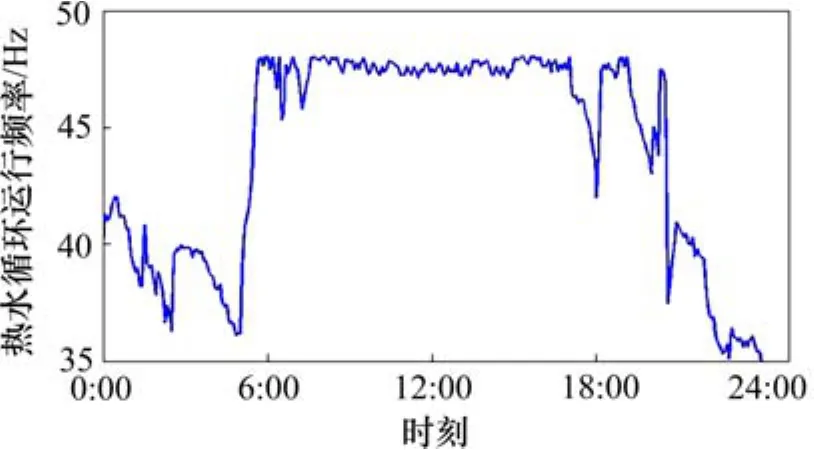
图9 热水循环泵运行频率变化曲线Fig.9 Varying curve of hot water circulating pump on frequency

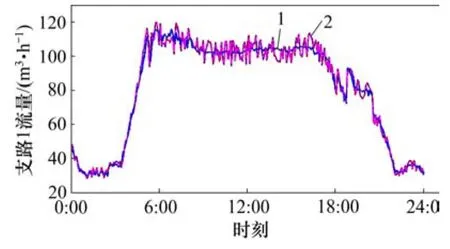
图10 支路1模型计算流量和实测流量对比变化曲线Fig.10 Contrast curve of predicated value and measured value on flow rate in the first branch

图11 支路2模型计算流量和实测流量对比变化曲线Fig.11 Contrast curve of predicated value and measured value on flow rate in the second branch

本文研究对象热水循环泵的型号和出厂日期完全一样(正常情况下开2台)：型号为DFG250-400B/A，额定功率为 75 kW，额定扬程为 42 m，额定流量为466 m3/h，2010年出厂。采用自动轮换运行，即效率基本相同，且各台循环泵的连接形式和管路结构完全一样，同一变频控制，故当2台循环泵运行时，若将板式换热器低温侧管路等价为循环泵泵体的一部分，则实质为2台同型号循环泵并联运行，2台循环泵的扬程一样，流量分半，即G=2Gp，利用2016-12-27所采集数据进行辨识，2016-12-28所采集数据进行精度验证。

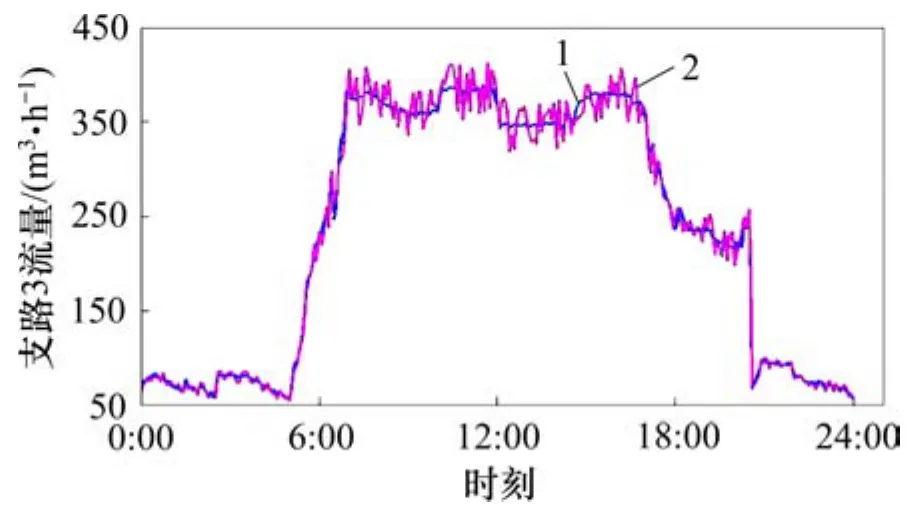
图12 支路3模型计算流量和实测流量对比变化曲线Fig.12 Contrast curve of predicated value and measured value on flow rate in the third branch

经辨识后，得到循环泵扬程模型参数c0=0.021 8，c1=0.360 5，c2=0.002 2；循环泵运行效率模型参数d0=-0.189 5，d1=0.273 8，d2=0.286 5。将辨识所得模型参数代入式(9)和(10)，将式(9)和(10)代入式(8)，得到2台循环泵组合下运行能耗模型：

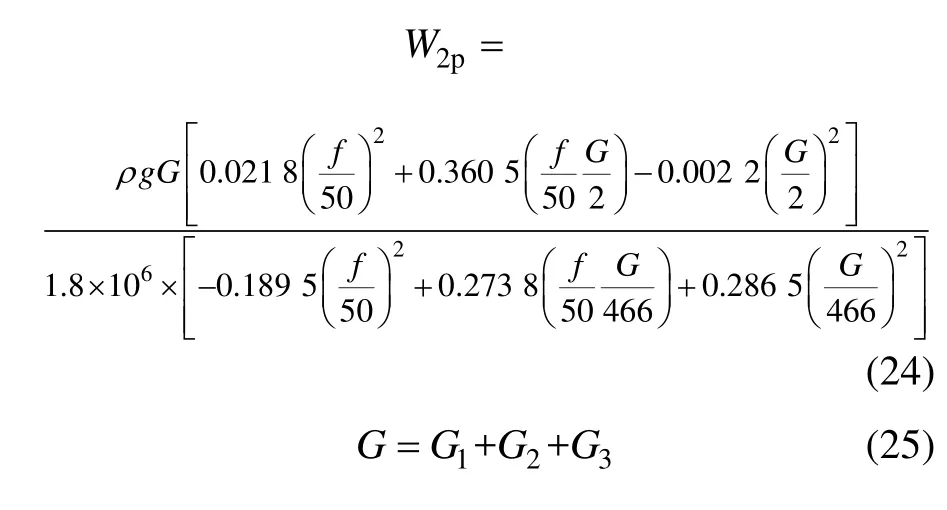
为验证水力工况下热水循环泵组合能耗模型的准确性，以2016-12-28所采集数据做对比，如图13和图14所示。从图13和图14可知：能耗模型精准度较高，最大相对误差基本在±8%之内，能满足后续仿真应用。

5.4 动力水力平衡优化模型

动态水力平衡的优化目标是在满足各支路水力平衡的前提下，使热水循环泵的运行能耗最低，其主要约束条件如下。

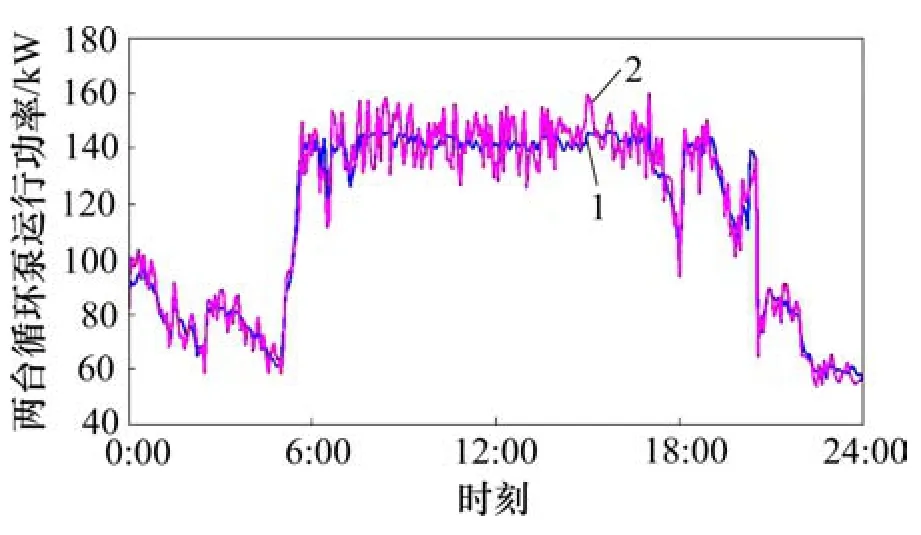
图13 循环泵组合能耗模型计算值和实测值对比变化曲线Fig.13 Contrast curve of predicated value and measured value on circulating pump energy consumption under combination driving mode

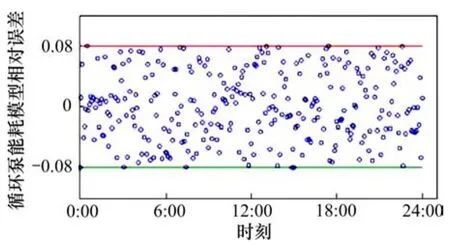
图14 循环泵组合能耗模型精度相对误差Fig.14 Relative error of circulating pump energy consumption under combination driving mode

根据热水循环泵运行经验及数据分析，将下限fmin设定为35 Hz，上限fmax设定为48 Hz。

根据本文项目所选电动调节阀的流量调节特性和实测节流能力，将下限φvi,min设定为10%，取值10，上限φvi,max设定为100%，取值100。

因此，该优化问题的目标函数及其约束条件可表示为以下形式：

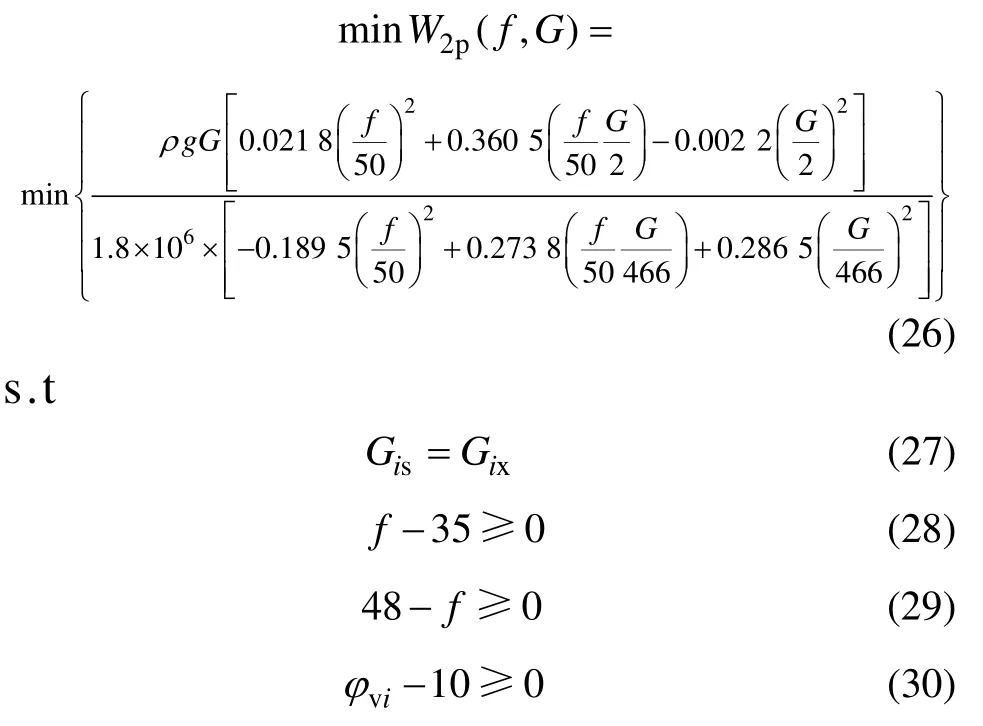
其中：

本节利用惩罚函数法，通过引进惩罚因子将约束条件引入目标函数，从而将有约束的最优化问题转化为无约束的最优化问题进行求解[14]，

建立罚函数如下式所示：

动态水力平衡优化问题的目标函数转化为无约束的最优化问题如下式所示：

5.5 基于遗传算法的优化流程

本文优化变量为4个，这4个变量的范围不大，故采用二进制编码方法，根据其以上4个变量的变化范围，取每个优化参数的二进制编码长度L=10。适应度函数用来计算种群每个个体的适应度值，并根据个体适应度的大小决定遗传到下一代的概率。一般适应度函数由优化问题的目标函数转化而来，对于动态水力平衡运行参数优化问题，其目标是最小值问题，而GA 通常处理最大值优化问题。本节在目标函数的基础上引入足够大的正数Cmax，将其减去目标函数，从而将动态水力平衡运行参数优化问题转化为最大值优化问题，其适应度函数可表示为

根据上述规则编制基于遗传算法的动态水力平衡优化运行参数组合优化计算程序，寻优过程包括：随机参数集的产生；目标函数值的求解；适应度函数的计算；依据适应度进行参数的选择、遗传和变异；子代替换父代重新寻优等。

1) 种群初始化，读取k时刻的室外温度和室内需求温度，代入式(12)，计算k时刻各支路流量需求值Gix,k。

2) 采集k时刻各支路调节阀开度φvi,k和热水循环泵运行频率fk组成输入参数集。

3) 将初始化的种群以及读取的输入参数集输入水力工况模型，计算得各支路在初始化参数下的流量Gis(φv1,φv2,φv3,f)。

4) 根据第 3)步获得的数据，计算个体的适应度值，根据适应度的大小对个体进行判断和处理，得到父代种群，然后对父代种群进行交叉、变异等操作，得到新的种群。

5) 反复进行步骤3)和4)的操作，直到满足算法的终止条件，算法的寻优搜索停止，并获得问题的最优解。最后通过解码，获得各支路k时刻的优化运行参数 (φv1,φv2,φv3,f)。

基于遗传算法的动态水力平衡参数优化流程如图15所示。

5.6 遗传算法参数确定与仿真

遗传算法控制参数对遗传算法的影响非常复杂，包括种群规模、交叉率和变异率等。为了使寻优的计算程序能够获得良好的计算效果，并提高程序的计算速率，本文对不同种群数量和遗传代数下的寻优计算效果进行了比较，结果显示，种群规模取60，最大允许进化代数取180，变异率取0.01，交叉率取0.6，优化算法的用时较短且种群能够在遗传结束后接近最优解。

图16所示分别为GA优化计算过程中各代种群的个体分布情况。从图16可知：初始种群是由随机函数产生，个体在寻优区间内分布较为均匀；在进化过程中，适应度低的个体被逐渐淘汰，而适应度高的个体被保留下来；随着进化代数的增加，群体中的个体分布逐渐趋于某一特定的区域；当种群进化到 180代时，个体已经集中到某个点，也就是该优化模型的最优解。GA优化算法所获得的最优解，即是各支路电动调节阀开度和热水循环泵运行频率的最优设定值，按此优化设定值进行优化控制就能实现动态水力平衡的优化调节。

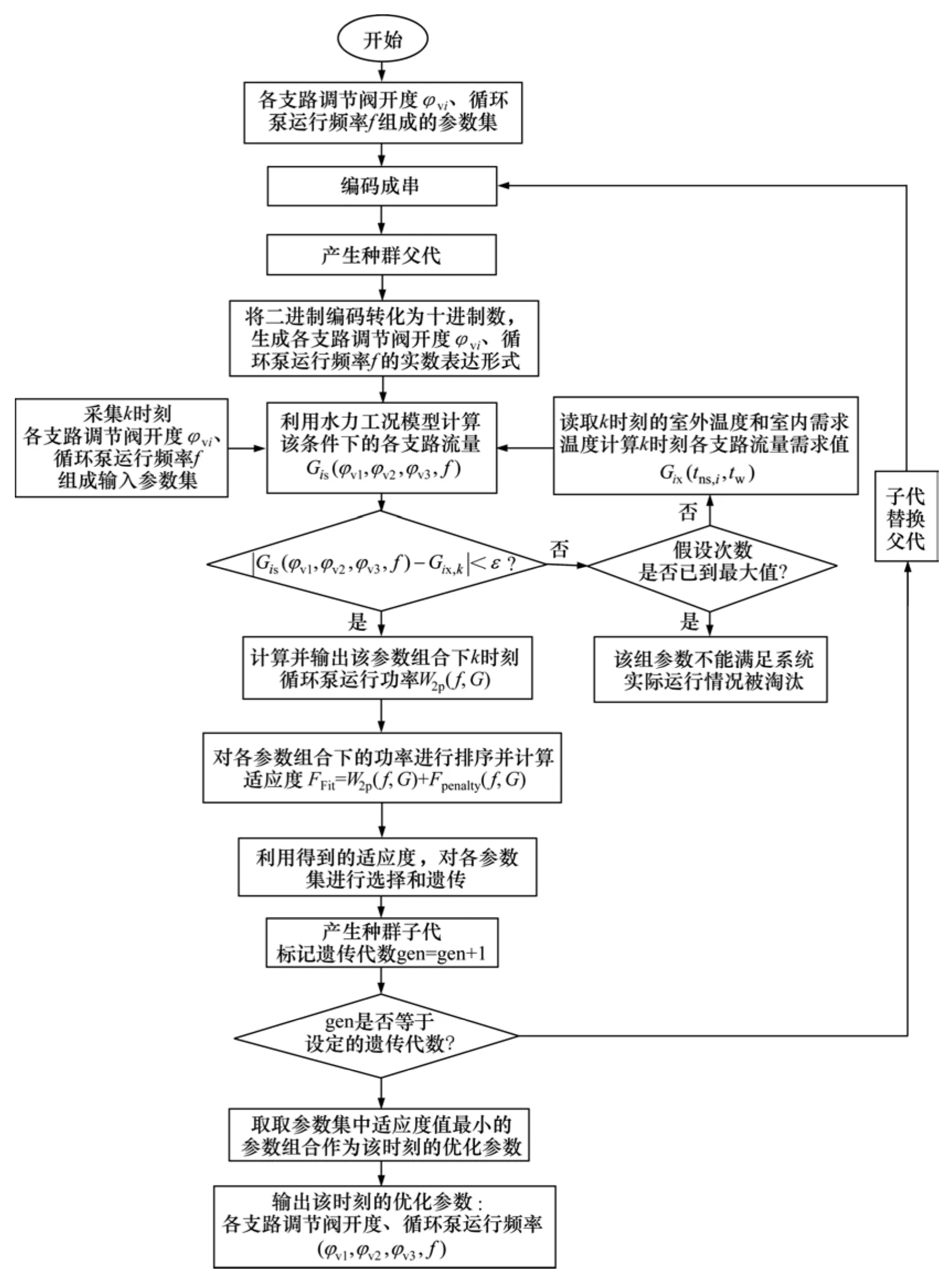
图15 动态水力平衡优化运行参数寻优流程图Fig.15 Flow chart for optimization of dynamic hydraulic balance

综合以上分析，建立的动态水力平衡运行参数优化模型如图17所示。

5.7 基于遗传算法的动态水力平衡运行参数优化

为验证上述寻优方法的有效性，选择2016-12-28的实际运行数据作为仿真实验数据来源和结果对比。2016-12-28室外温度变化曲线见图18。

支路 1建筑为学生食堂，供热设计流量约 120 m3/h，5:00—19:30时段室温要求为18 ℃(正常供热)，其余时段为10 ℃(低温供热)；支路2建筑为宿舍，供热设计流量和为292 m3/h，全天正常供热；支路3建筑为教学楼和实验楼，供热设计流量和为406 m3/h，7:30—22:00时段室温要求为18 ℃(正常供热)，其余时段为 10 ℃(低温供热)。

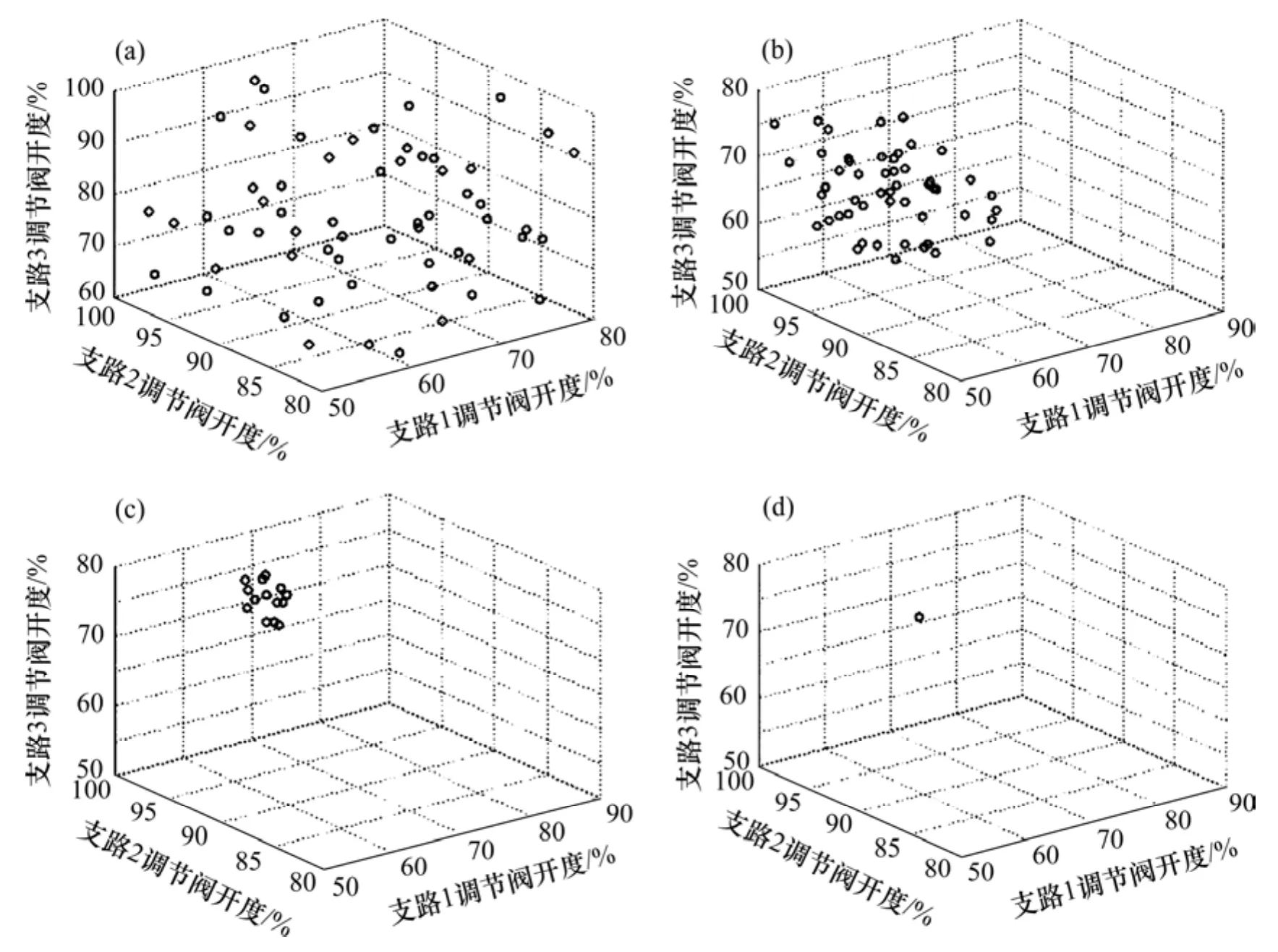
图16 GA优化计算过程中各代种群的个体分布情况Fig.16 Distribution of different generations in the process of GA optimization

图17 动态水力平衡运行参数优化模型原理图Fig.17 Schematic diagram of parameters optimization model for dynamic hydraulic balance

考虑到建筑热惰性，早上须提前加热，晚上可提前降温，本文低温供热和正常供热的模式转换时间不会严格按照上述时间点转换。该换热站供热建筑为非节能建筑，保温性一般，经过长期现场测试，发现当室外温度在0～5 ℃时，提前1 h停热，室内温度从18 ℃降至16 ℃左右，现场基本无投诉；室外温度为-5～0 ℃时，提前1.5 h供热，室内温度从10 ℃升至13～14 ℃，该温度虽然不属于热舒适性温度，但是现场基本无投诉，原因可能是当人刚从室外低温空气中进入建筑时，该温度是人体可接受的，因此，本文视其为合理的。因此，该日支路 1正常供热模式实际运行时段为3:30—18:30，支路 3正常供热模式实际运行时段为6:00—21:00。各时刻流量需求值(优化值)和实测值见图19，各支路平均室内温度设定值与实测值见图20。

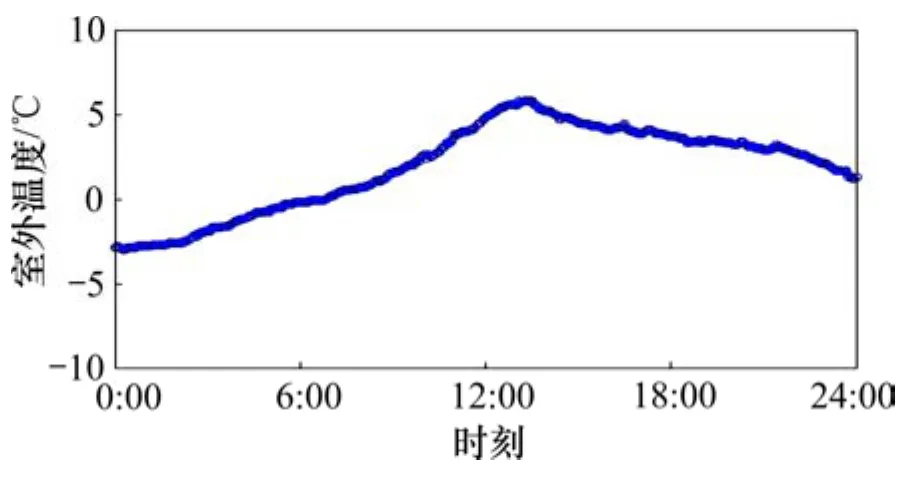
图18 仿真实验日室外温度变化曲线Fig.18 Simulation of varying curve of outside temperature in day of experiment

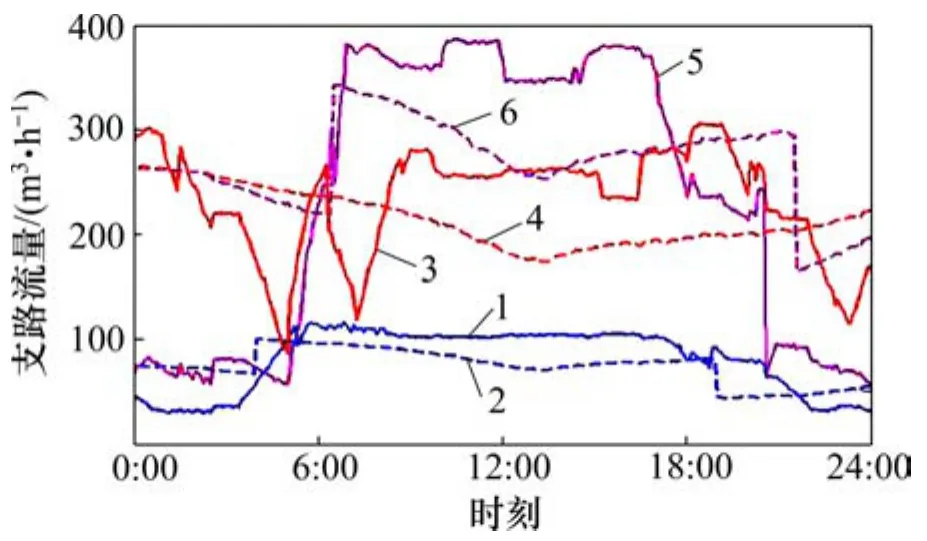
图19 仿真实验日各支路流量逐时实测值和优化值Fig.19 Simulation of predicated value and optimal value on flow of each branch in day of experiment

各支路逐时流量优化值与实测值相差均大，原因在于实际运行过程中电动调节阀开度是完全通过检测室内温度调节开度以改变流量，为被动式调节；仿真实验中流量需求值根据室外气温和室内设定温度计算所得，为主动式调节。在实际运行过程中，可能存在某时刻室外温度较低而室内温度高于设定温度上限，调节阀调小开度使流量减小，而用流量需求公式受室内需求温度和室外温度影响较大。但是，主动式流量调节是应对供热需求负荷实时变化的有效手段，能解决并联支路间的水力工况扰动问题。

从1 d内流量平均值看，各支路流量优化值和实测值的平均值相差很小：支路 1流量优化平均值为74.07 m3/h，实测平均值为80.26 m3/h；支路2流量优化平均值为214.41 m3/h，实测平均值为232.66 m3/h；支路3流量优化平均值为266.58m3/h，实测平均值为233.04 m3/h；总流量优化平均值为555.07 m3/h，实测平均值为545.97 m3/h。

图20 仿真实验日各支路建筑室温设定值和平均实测值Fig.20 Average temperature expected value and measured value of each branch building in simulation experiment day

从图20可知：

对支路1，0:00—5:00，室温设定值为10 ℃时，平均实测值为 12.1 ℃；5:00—19:30,室温设定值为18 ℃时，平均实测值为18.5 ℃；19:30—24:00，当室温设定值为10 ℃时，平均实测值为15 ℃。

对支路2，0:00—24:00，当室温设定值为18 ℃时，平均实测值为18.5 ℃。

对支路3，0:00—7:30，当室温设定值为10 ℃时，平均实测值为13.2 ℃；7:30—22:00，当室温设定值为18 ℃时，平均实测值为19 ℃；22:00—24:00，当室温设定值为10 ℃时，平均实测值为16.5 ℃。

正常供热模式下，室内平均实测温度比较接近室温设定值，低温供热模式下，由于建筑热惰性，实质上每日降到10 ℃的时段很短，而一旦低于10 ℃，建筑电动调节阀会打开，提供热水加热室内空气，所以，低温供热模式下的平均实测温度会大于或等于设定的10 ℃。

图21所示为仿真实验日各支路调节阀逐时开度实测值和优化值。由图21可知：总有1个支路调节阀开度优化值接近 100%，说明优化过程中，为保证流量需求最大支路水力平衡度，同时为减少调节阀引起的阻力损失，必有某个调节阀开度为 100%。同时，从1 d内调节阀开度平均值看，优化平均值明显大于实测平均值：支路1调节阀开度优化平均值为68.16%，实测平均值为 54.72%；支路 2流量优化平均值为96.61%，实测平均值为70.22%；支路3流量优化平均值为 64.28%，实测平均值为 49.09%。各支路电动调节阀的流量调节是实现各支路水力平衡的主要手段，而在管网中，循环泵高频率、电动调节阀小开度状态与循环泵低频率、电动调节阀大开度状态实现的效果一样的，因此，本文提出在保证各支路水力平衡前提下，尽可能增大调节阀开度减少管网阻力，同时降低循环泵频率以实现节能运行。

图22所示为仿真实验日循环泵逐时运行频率实测值和优化值。

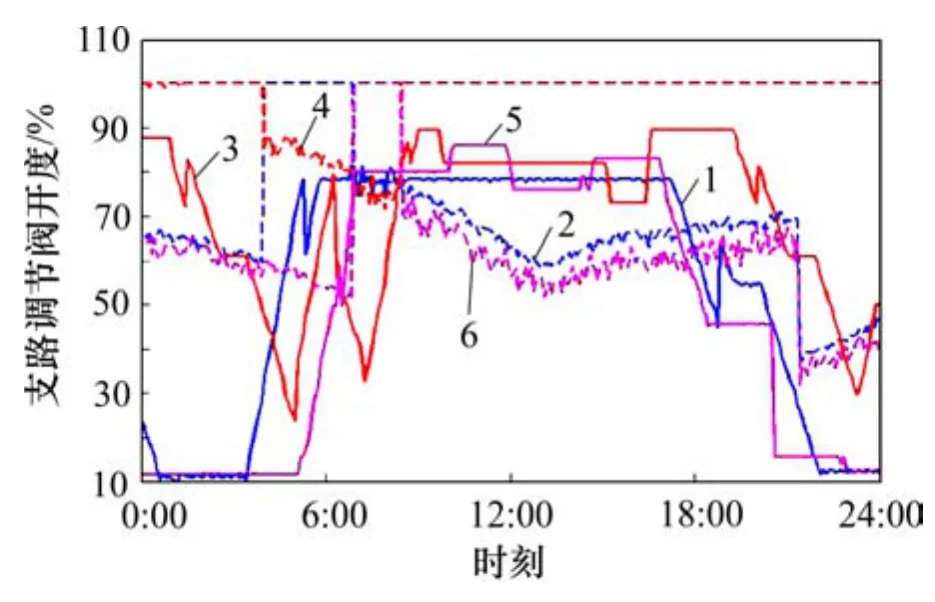
图21 仿真实验日各支路调节阀逐时开度实测值和优化值Fig.21 Simulation of predicated value and optimal value of hourly control valve openness of each branch in day of experiment

图22 仿真实验日循环泵逐时运行频率实测值和优化值Fig.22 Simulation of predicated value and optimal value on circulating pump frequency in day of experiment

循环泵运行频率优化值与各支路调节阀开度相关，因调节阀开度增大，1 d内循环泵运行频率优化平均值为42.16 Hz，实测平均值为43.98 Hz，使循环泵运行能耗减小。

循环泵逐时节能率有正有负，与循环泵运行频率变化曲线相似，总体节能率为12.27%，节能效果比较明显。因此，对循环泵运行频率和各支路调节阀开度进行合理设置，既可保证各支路水力平衡，又可有效降低循环泵的运行能耗。

6 结论

1) 提出了基于遗传算法的动态水力平衡优化调节方法。在二次管网水力平衡调节必要性分析的基础上，利用图论建立了精度较高的管网水力工况模型和循环泵运行能耗模型，并以循环泵运行能耗最小为目标，以各末端支路水力平衡度为主要约束条件，建立了基于遗传算法的动态水力平衡优化调节模型，实时优化循环泵的运行频率和各支路电动调节阀的开度。

2) 通过实际系统的仿真实验与实测数据进行比较，本文所提优化调节方法相对变压差变流量调节方法循环泵运行能耗降低12.27%，节能效果较明显，为复杂管网动态水力平衡调节方法的研究和工程实现提供良好的思路，同时，可为多执行机构的管网动态水平衡调节提供参考。