一种改进PBS的无线传感器网络时钟同步方法SCRT

车步波 郭改枝

关键词： 无线传感网络; PBS; 时钟同步; SCRT; 时钟偏移; 频率偏移

中图分类号： TN926?34; TP391.9               文献标识码： A                    文章编号： 1004?373X（2019）04?0031?06

An improved PBS based clock synchronization method

SCRT for wireless sensor networks

CHE Bubo， GUO Gaizhi

（School of Computer and Information Engineering， Inner Mongolia Normal University， Hohhot 010022， China）

Abstract： In allusion to the problem that the synchronization range of sensor nodes is limited when the pairwise broadcast synchronization （PBS） method is used to conduct clock synchronization for wireless sensor networks （WSNs）， an improved PBS based clock synchronization method SCRT is proposed for WSNs. In the method， the sender?receiver （SR） synchronization and receiver?only （RO） synchronization are combined. The cluster head nodes in the packet clustered network exchange the clock information with the reference nodes， and the member nodes adjust the local clock according to the reference time stamps carried in the cluster head sending and receiving clock messages， so as to achieve clock synchronization. It is found that the clock offset estimation and frequency offset estimation are optimal in the comparison with the calculated Cramer?Rao Lower Bound （CRLB） in the Matlab simulation. The experimental results show that in comparison with the PBS scheme， the clock synchronization method can increase the synchronization range of the nodes， significantly reduce the synchronization errors of the entire network， and improve the synchronization efficiency.

Keywords： wireless sensor network; PBS; clock synchronization; SCRT; clock offset; frequency offset

0  引  言

无线传感器网络（WSN）由于其相对于传统网络具有规模大、自组织能力强、廉价、动态性能好等优点，因此在军事防卫、环境监测、医疗卫生、科学研究及工业、民用和家用网络等领域具有广泛的应用[1]。无线传感器网络的一个技术支撑是时钟同步[2?3]，比如在数据融合、移动物体的速度测量[4]、时分多址接入等技术的应用上都需要无线传感器网络中节点具有一致的时钟消息，因此时钟同步非常重要。

目前，在无线传感器网络时钟同步协议的研究中，根据是否有参考节点可将时钟同步协议分为两种：一种是基于参考节点的时钟同步协议;另一种是分布式的时钟同步协议。本文研究的是基于参考节点的时钟同步协议，即发送者?接收者（SR）和仅接收者（RO）。对于SR，文献[5]中提出的RBS（Reference Broadcast Synchronization）是基于参考节点的时钟同步协议的代表。协议刚开始会将其中的一个节点选作参考节点，之后剩余的节点会周期性地和这个参考节点同步，以致使整个网络的时钟同步。文献[6]提出TPSN（Times Synchronization Protocol for Sensor Networks），其原理是选一个节点作为根节点（或参考节点），在这个根节点的基础上，整个网络会逐渐形成一个树状结构，而网络中的节点都与其父节点同步后整个网络的时钟就能够同步。文献[7]提出FTSP（Flooding Time Synchronization Protocol），其原理是选取一个节点作为根节点之后，根节点会以Flooding“泛洪”传播的方式向整个树状网络周期性地传播自己的时钟信息从而达到全网时钟同步。对于RO，文献[8]提出PBS，一组节点可以通过仅监听一对节点之间交换的时钟消息来同步。该方法可以显著降低消息传递的能量和带宽。通过查阅文献可知，若N为同步过程所需的定时消息数目，L为网络中整体传感器节点的数目，对于RBS，FTSP，TPSN和PBS来说，它们的能量消耗分别为：[NRBS=N+LL-12]，[NFTSP=NL]，[NTPSN=2NL-1]和[NPBS=2N]。通过对比发现，PBS在每个同步周期中仅需要2N个定时消息，NPBS的大小不取决于网络中传感器的数量，这将会节省巨大的能量，而且网络规模越大，此优势越明显。因此，PBS相对于RBS，TPSN和FTSP等在能量节省方面有巨大优势，是一种较为理想的同步方法。然而，这种方法也有限制性条件：簇内成员节点只有位于簇头节点和参考节点的通信范围内才能达到相对比较好的同步效果。为了解决这个问题，提出了携带参考时间戳同步方法，即SCRT。它利用雙层结构的WSN，每个簇都有一个簇头节点，簇头通过与网络中的参考节点消息交换进行时钟同步[9]。SCRT要求在簇头消息中附加参考时间戳，以便簇内成员可以监听它们的时钟变化进而调整自己的时钟。

1  SCRT算法

假设在一个成簇网络中，簇头在参考节点的通信范围内（由于功率约束，传感器的通信范围被严格限定为半径取决于传输功率的无线电几何圆内[9]）。对于文献[7]中的PBS，簇头通过双向消息交换与参考节点进行同步;位于两圆交集内的簇内成员通过监听簇头和参考节点之间的消息交换来进行成对同步。节点放置模型图如图1所示。假定[H]是簇头节点，[G]是参考节点，[M1]～[M5]为簇内成员节点，那么只有成员节点[M1]和[M2]可以使用RO方法同步。而位于公共通信范围之外的成员节点（[M3]，[M4]和[M5]）不能监听由参考节点发送的时钟信息，所以它们的同步只能通过多跳同步。而这会导致同步精度的下降以及同步误差的增大。但SCRT解决了这个不足，即利用通信范围之外的成员节点监听簇头发送的所有时钟消息，以及[H]和[G]之间的基于SR方法的多轮双向信息交换的同步。因此，第[i-1]轮中，参考节点发送的时钟消息将被捎带在同步消息中，以便在第[i]轮中由簇头发送，这样所有成员节点不管它们的位置如何都能通过监听时钟消息来与参考节点同步。当簇头[H]根据参考节点[G]采用SR方法进行时钟同步时，SCRT能够让簇内的所有成员节点[Mj]采用RO方法进行时钟同步，无论这些成员节点是否在[H]和[G]的通信范围内。图2为SCRT时钟同步消息交换模型，时钟消息进行[N]轮交换。要进行SR同步，节点需要发送和接收同步请求和确认消息的时间戳;同时，节点得到参考节点的接收时间和自己的同步请求消息的接收时间就可以进行RO同步。

假定在第[i]轮消息交换时，在节点[H]的本地时钟上获得同步请求发送时间戳和消息确认接收时间戳分别为[T（H）1，i]和[T（H）4，i]，在节点[G]的本地时钟上得到同步请求发送时间戳和消息确认接收时间戳分别为[T（G）2，i]和[T（G）3，i]，在節点[Mj]的本地时钟上得到同步请求接收时间戳[T（Mj）2，i]。在每个同步轮[i]，节点[H]在[T（H）1，i]时发送一个同步请求消息给节点[G]，该消息携有发送时间戳[T（H）1，i]和节点[G]之前接收同步请求的接收时间[T（G）2，i-1]，携带[T（G）2，i-1]可以让处于[G]的通信范围外的节点进行RO同步。节点[G]在[T（G）2，i]时收到同步请求后，会在[T（G）3，i]返还发送一个包含时间戳[T（G）2，i]和[T（G）3，i]的确认消息，节点[H]收到确认消息后，会记录其到达时间。节点[H]使用4个时间戳信息可以按照SR同步方法的原理与节点[G]同步。由于无线通信介质的广播性质，成员节点可以完全或部分地监听这种双向通信，这取决于它们是否在[G]和[H]的通信范围内。在第[i]轮收到同步请求后会记录其到达时间，还会得到本地接收时间。因为节点[G]和[Mj]都处于节点[H]的广播范围，它们有可能会在相同的时间收到同步请求消息。这样，依照自己本地时钟上得到时间戳和节点上的时间戳直接和[G]进行同步，而不需要和其他节点交换消息。

2  RO和SR时钟偏移和频率偏移估计

使用一阶线性模型来表示节点间的相对时钟，包括时钟偏移和频率偏移的影响，即：

[T（G）2，i=ω（HG）T（H）1，i+δ（HG）+d（HG）+Xi]       （1）

[T（G）3，i=ω（HG）T（H）4，i+δ（HG）-d（HG）-Yi]        （2）

[T（M）2，i=ω（HM）T（H）1，i+δ（HM）+d（HM）+Zi]      （3）

式中：[δ（HG）]和[ω（HG）]分别为节点[H]和[G]间的相对时钟偏移和频率偏移;[δ（HM）]和[ω（HM）]分别为节点[M]和[H]间的相对时钟偏移和频率偏移;[d（HG）]和[d（HM）]分别表示从节点[H]到[G]和节点[H]到[M]的传输固定延迟。[XiNi=1]，[YiNi=1]和[ZiNi=1]分别表示从节点[H]到[G]、节点[G]到[H]和节点[H]到[M]的传输随机延迟。假定[XiNi=1]，[YiNi=1]和[ZiNi=1]服从均值为0，方差为[σ2]的正态分布，这样，固定延迟可以用能够被确定的传输时间来表示，用数据包大小和信号传播模型来估计。由式（1）～式（3）可得出节点[M]和[G]之间的时钟偏移和频率偏移。

[T（G）2，i-T（M）2，i=ω（MG）T（H）1，i+δ（MG）+d（HG）-d（HM）+Xi-Zi] （4）

令[d?d（HG）-d（HM）]，[Ti?T（G）2，i-T（M）2，i-d]，[Ki?Xi-Zi]，代入式（4）可得：

[Ti=ω（MG）T（H）1，i+δ（MG）+Ki] （5）

因为随机延迟[XiNi=1]和[ZiNi=1]服从正态分布，那么[KiNi=1]也服从正态分布，则基于[KiNi=1]的似然函数[L1]为：

[L1=12πσ2N·e-12σ2i=1NTi-δMG-ωMGTH1，i2]  （6）

此时想要得到[δ（MG）]和[ω（MG）]的极大似然估计，需将式（6）化为：

[L1=12πσ2N2·e-12σ2i=1NTi-δMG-ωMGTH1，i2]

将其取对数为：

[ln L1=-12σ2i=1NTi-δ（MG）-ω（MG）T（H）1，i2]

并求[δ（MG）]的偏导数[?ln L1?δ（MG）]，令[?ln L1?δ（MG）=0]得到[δ（MG）]的极大似然估计为：

[δ（MG）=i=1N（Ti-T（H）1，iω（MG））N]  （7）

同理可得[ω（MG）]的极大似然估计为：

[ω（MG）=i=1NT（H）1，iTi-δ（MG）i=1NT（H）1，ii=1N（T（H）1，i）2] （8）

联合式（7）和式（8）并将[Ti]替换为[T（G）2，i-TM2，i-d]，假设固定延迟是对称的，那么[d=0]，则时钟偏移和频率偏移为：

[ω（MG）=Ni=1Nj=1NT（H）1，j（T（G）2，j-T（M）2，j）-i=1Nj=1NT（H）1，i（T（G）2，j-T（M）2，j）Ni=1N（T（H）1，i）2-i=1Nj=1NT（H）1，iT（H）1，j] （9）

[δ（MG）= i=1Nj=1N（T（H）1，i）2（T（G）2，j-T（M）2，j）-i=1Nj=1NT（H）1，i（T（H）1，j（T（G）2，j-T（M）2，j））Ni=1N（T（H）1，i）2-i=1Nj=1NT（H）1，iT（H）1，j] （10）

为了对时钟偏移和频率偏移的精确度进行评估，计算出了相应的克拉美罗界（Cramer?Rao Lower Bound，CRLB）。CRLB给出了任何无偏估计量方差的理论下限。CRLB可通过费雪信息矩阵的倒数[I-1（θ）]获得：

[I-1（θ）=σ2Ni=1N（T（H）1，i）2-i=1NT（H）1，i2·                 i=1N（T（H）1，i）2    -i=1NT（H）1，i -i=1NT（H）1，i             N]  （11）

則根据费雪信息得出对于RO方法时钟偏移和频率偏移的CRLB分别为[10]：

[var（ω（MG））≥Iθ1，1=σ2i=1N（T（H）1，i）2Ni=1N（T（H）1，i）2-i=1NT（H）1，i2] （12）

[var（δ（MG））≥Iθ2，2=Nσ2Ni=1N（T（H）1，i）2-i=1NT（H）1，i2] （13）

根据相对时钟模型式（1）和式（2），将得出节点[H]和[G]之间的时钟偏移和频率偏移。令[T′2，i?T（G）2，i-d（HG）]，[T′3，i?T（G）3，i-d（HG）]，代入式（1）、式（2）可得：

[T′2，i=ω（HG）T1，i+δ（HG）+Xi] （14）

[T′3，i=ω（HG）T4，i+δ（HG）+Yi] （15）

因为随机延迟[XiNi=1]和[YiNi=1]服从正态分布，则基于[XiNi=1]和[YiNi=1]的似然函数为：

[L2=12πσ2Ne-12σ2i=1N（Xi）2+（Yi）2]   （16）

由式（16）可知，[ln L2=-12σ2i=1N（Xi）2+（Yi）2]，根据式（14）、式（15）将[Xi]和[Yi]代入，得到：[?ln L2?δHG=]

[12σ2i=1N（T′2，i+T′3，i）-ω（HG）i=1N（T（H）1，i+T（H）4，i）-2Nδ（HG），]

令[?ln L2?δ（HG）=0]，求得[δ（HG）]的极大似然估计为：

[δ（HG）=i=1N（T′2，i+T′3，i）2N-ω（HG）·i=1N（T（H）1，i+T（H）4，i）2N]  （17）

同理可知[ω（HG）]的极大似然估计为：

[ω（HG）=i=1N（T（H）1，iT′2，i+T（H）4，iT′3，i）i=1N（T21，i+T24，i）-δ（MG）·i=1N（T（H）1，i+T（H）4，i）i=1N（T21，i+T24，i）]  （18）

联合式（17）、式（18）并替换[T′2，i?T（G）2，i-d（HG）]，[T′3，i?T（G）3，i-d（HG）]，则时钟偏移和频率偏移为：

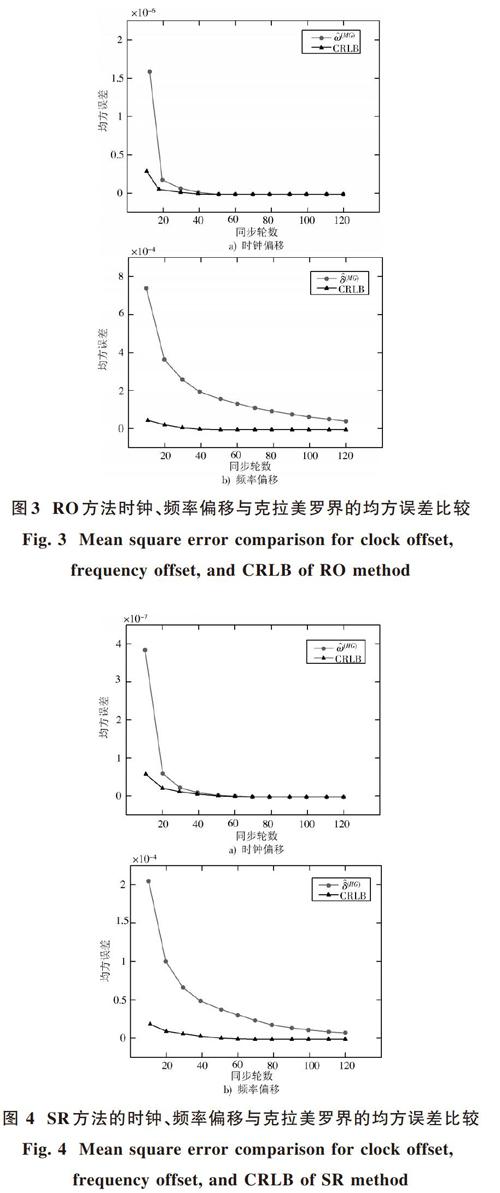
由式（9）、式（10）可知，根据[T（H）1，i]，[T（G）2，i]和[T（Mj）2，i]的时间戳信息的变化来调节[M]和[G]之间的时钟偏移[ω（MG）]和频率偏移[δ（MG）];同理，由式（19）、式（20）可知，根据[T（H）1，i]，[T（G）2，i]，[T（G）3，i]和[T（H）4，i]的时间戳信息的变化来调节[H]和[G]之间的时钟偏移[ω（HG）]和频率偏移[δ（HG）]。通过Matlab进行仿真，图3和图4给出了RO和SR时钟偏移均方误差、频率偏移均方误差和克拉美罗界的对比。由图3可知，使用RO方法时、随着同步轮数N的取值变大，时钟偏移与频率偏移均方误差逐渐减小，且当N[≥]50后，时钟偏移均方误差与克拉美罗下界基本重合，而频率偏移均方误差逐渐趋近于克拉美罗下界。由图4可知，使用SR方法时钟偏移与频率偏移均方误差曲线变化基本和RO方法一样，得出的时钟偏移与频率偏移均方误差要小于使用RO方法，但它们都最终收敛于CRLB，因此可以确定得到的时钟偏移估计与频率偏移估计为最优估计。

3  实验以及结果分析

本文使用基于CC2530芯片的ZigBee节点进行实验来评估PBS和SCRT的同步误差，如图1所示，进行节点布控，选用4个节点分别放在[G]，[H]，[M1]，[M3]的位置。簇头[H]和成员节点[M1]和[M3]使用SCRT和PBS和参考节点[G]进行同步。

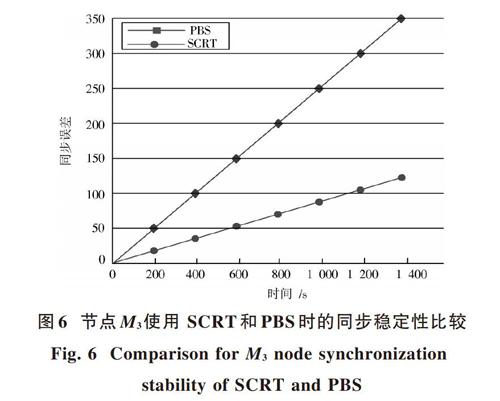
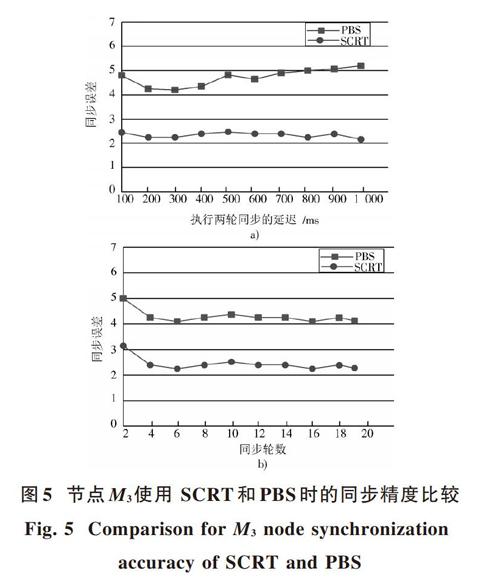
在SCRT和PBS中，[H]和[M1]分别使用SR和RO方法与[G]进行一跳同步。然而，[M3]使用SCRT的RO方法与[G]进行同步需要一跳，但是[M3]使用PBS的SR方法实现与[G]的同步需要两跳。由于[H]，[M1]以相同的方式使用SCRT或PBS进行同步，它们将得到相同的同步误差，因此，以节点[M3]进行同步时的精度（见图5）和稳定性（见图6）来评估SCRT和PBS的同步误差。

根据图5可知，随着执行两轮同步后的延迟的增加，使用PBS同步误差逐渐增大，而使用SCRT同步误差波动范围较小，且相对平稳，总体同步误差小于PBS。而随着同步轮数的增加，SCRT和PBS的同步误差都在一个相对固定的范围内波动，但SCRT的总体同步误差也小于PBS。因此，在同步精度方面，SCRT要好于PBS。从图6可以看出，随着时间的增加，与SCRT相比使用PBS时同步误差增加更快，且在同一时间，使用PBS时同步误差明显大于使用SCRT。因此，就同步精度和稳定性的比较可知SCRT比PBS的性能更好。

4  结  语

本文提出一种改进PBS的无线传感网络时钟同步方法SCRT，并给出了RO和SR的均方误差与克拉美罗界的对比，得出时钟偏移与频率偏移估计为最优估计。通过实验证明SCRT在同步精度与稳定性方面强于PBS，节点的同步范围也大于PBS。

参考文献

[1] 张忠厚，赵龙.无线传感网络节能跨层调度算法[J].计算机系统应用，2012，21（8）：48?51.

ZHANG Zhonghou， ZHAO Long. Energy?efficient cross?layer scheduling algorithm based on WSN [J]. Computer systems & applications， 2012， 21（8）： 48?51.

[2] LIU B， REN F， SHEN J， et al. Advanced self?correcting time synchronization in wireless sensor networks [J]. IEEE communications letters， 2010， 14（4）： 309?311.

[3] 王义君，钱志鸿，王桂琴，等.无线传感器网络能量有效时间同步算法研究[J].电子与信息学报，2012，34（9）：2174?2179.

WANG Yijun， QIAN Zhihong， WANG Guiqin， et al. Research on energy?efficient time synchronization algorithm for wireless sensor networks [J]. Journal of electronics & information technology， 2012， 34（9）： 2174?2179.

[4] ZHANG W， YIN Q， CHEN H， et al. Distributed angle estimation for localization in wireless sensor networks [J]. IEEE transactions on wireless communications， 2013， 12（2）： 527?537.

[5] ELSON J， GIROD L， ESTRIN D. Fine?grained network time synchronization using reference broadcasts [J]. ACM SIGOPS operating systems review， 2002， 36（SI）： 147?163.

[6] GANERIWAL S， KUMAR R， SRIVASTAVA M B. Timing?sync protocol for sensor networks [C]// Proceedings of the 1st International Conference on Embedded Networked Sensor System. Los Angeles： Scientific Research， 2003： 138?149.

[7] MAROTI M， KUSY B， SIMON G， et al. The flooding time synchronization protocol [C]// Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems. Baltimore： ACM， 2004： 39?49.

[8] NOH K L， SERPEDIN E. Pairwise broadcast clock synchronization for wireless sensor networks [C]// Proceedings of IEEE International Symposium on a World of Wireless， Mobile and Multimedia Networks. Espoo： IEEE， 2007： 1?6.

[9] 蒋智鹰，陈勇，胡冰，等.无线传感器网络时间同步算法研究[J].计算机工程与应用，2017，53（1）：1?8.

JIANG Zhiying， CHEN Yong， HU Bing， et al. Research on time synchronization algorithm for wireless sensor networks [J]. Computer engineering and applications， 2017， 53（1）： 1?8.

[10] DJENOURI D， MERABTINE N， MEKAHLIA F Z， et al. Fast distributed multi?hop relative time synchronization protocol and estimators for wireless sensor networks [J]. Ad hoc networks， 2013， 11（8）： 2329?2344.