机载塔康无源定位方法研究

李亚军

(中国西南电子技术研究所，四川 成都 610036)

0 引言

塔康作为一种广泛应用的无线电导航设备，能够同时提供载机相对于塔康站的方位和斜距信息[1-2]。然而，塔康为了达到远距离测距的战术指标，其峰值辐射功率往往较大，且辐射的波束也较宽，信号形式相对固定，这对于全机保持无线电静默是相当不利的。据文献报道，一些先进的无源侦收系统已具备塔康导航信号的检测、分选和识别能力，并能通过塔康信号实现定位，获取机载平台位置信息，进而实施欺骗干扰。文献[3-5]研究了塔康的方位和时延估计方法。文献[6-7]在时差估计的基础上，研究了塔康等特殊信号的定位估计，能够准确输出定位结果。文献[8-10]基于塔康系统的识别信息，实现了对塔康信号的干扰，达到了很好的干扰效果。综上所述，研究塔康在无线电静默条件下的使用对于保证飞机的生存能力至关重要[11]。本文从塔康不辐射、仅测向的角度出发[12-13]，研究了其无源定位技术并分析了定位精度。

1 无源定位原理

塔康在无线电静默时，丧失了测距的功能，仅提供方位信息。本文的思路是通过塔康双站测向，并结合高度信息，实现测向交叉定位[14-15]。首先得到塔康相对于台站S1的方位e1，飞机的位置被确定为一个以S1为原点，向外发散的垂直于地面的90°圆弧面，半径不超过台站1的最大作用距离R1max。同理，得到塔康相对于台站S2的方位e2，飞机的位置再被确定为一个以S2为原点，向外发散的垂直于地面的90°圆弧面，半径同样不超过台站2的最大作用距离R2max。2个圆弧面在空间中相交为一条垂直于地面的垂线，在高度范围内，飞机可以在该垂线上的任意位置，因此存在定位模糊，需要高度值H解模糊[16-18]。

塔康基于地面台站测向信息实现定位的基本原理如图1所示。忽略各台站的高差差异，且飞机在地面的垂直投影和各台站在同一平面。

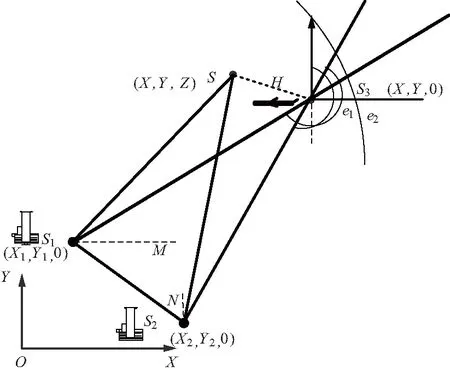
图1 塔康双站定位原理

图1中，

(1)

(2)

且∠S1S3S2=e1-e2，在地面投影的△S1S2S3中，根据正弦定理得：

(3)

于是有

(4)

式中，

(5)

解得：

(6)

由式(6)可知，在高度值H已知的情况下，飞机在地面上方Z=H>0，飞机的位置S(X，Y，Z)存在唯一解[19]。

在实际应用中，由于信道是标准化的且功能通过软件实现，满足上述塔康双收的条件，塔康双站测向交叉定位具备工程实现的可能性。塔康双站定位从射频前端、信道以及后端信号和信息处理的实现如图2所示。

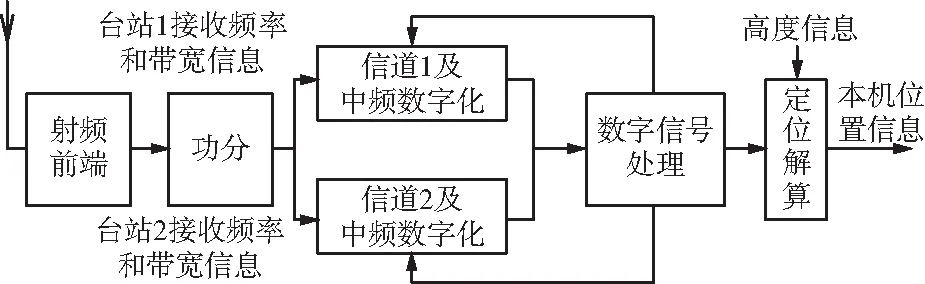
图2 塔康双站定位实现框图

2 定位误差分析

图3给出了塔康双站定位的定位误差，分析了误差的各种边界条件。

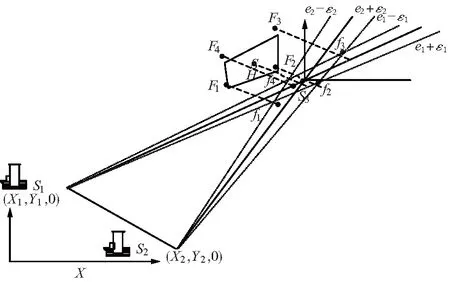
图3 塔康双站定位误差

考虑方位测量误差，塔康无源定位系统将存在定位误差。假定塔康相对于台站1的测位误差为ε1，相应的实测方位为e1r∈((e1-ε1)，(e1+ε1))，台站2的测位误差为ε2，实测方位e2r∈((e2-ε2)，(e2+ε2))。在高度H平面上，有4个相交点F1，F2，F3，F4构成不规则四边形F1F2F3F4，该四边形决定了定位误差。将该四边形垂直投影至地面，得到四边形f1f2f3f4，该四边形对于研究定位误差具有同等意义。

以边界S3f1为例，

(7)

(8)

式中，i=1，2为台站编号。

(9)

同理可得：

(10)

(11)

(12)

(13)

(14)

(15)

综上可得：

(16)

(17)

式中，j=1，2，3，4。j，p，q的关系为:

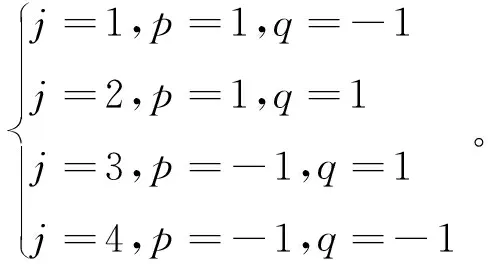
由上可鉴，定位误差既可以在以台站S1为顶点的三角形中计算，也可以在以台站S2为顶点的三角形中计算。定位误差涵盖了4个方向，分别对应方位测量误差的4个边界。

任何导航系统都有相应的最大作用距离Rmax。尤其是无线电导航系统，这一指标特别重要。在上面的讨论中，一旦考虑了作用距离，那么飞机在地面上的投影区域有可能不再是封闭区域。台站S1的最大作用距离是R1max，台站S2的最大作用距离是R2max。如图3所示，若S1F1，S1F2，S1F3，S1F4中的任何一个大于R1max或者S2F1，S2F2，S2F3，S2F4中的任何一个大于R2max，那么便不能确定飞机在地面上的投影区f1f2f3f4。

3 仿真结果与分析

仿真条件1：假设台站1的位置为(0，0，0)，台站2的位置为(1 km，-1 km，0)，方位测量误差ε1=ε2=1°，飞机位置X∈(-500 km，500 km)，Y∈(-500 km，500 km)。塔康双站定位的定位误差如图4所示。

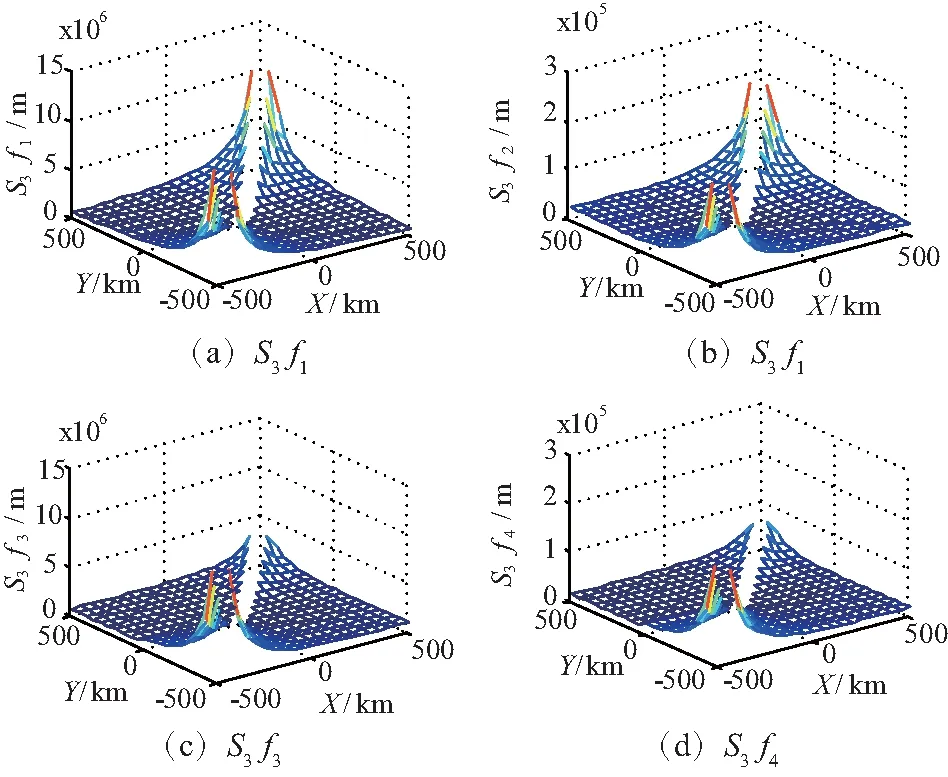
图4 塔康双站定位的定位误差仿真结果

由图4可知，无论是以台站1还是以台站2为顶点计算定位误差，结果基本一致。当X=Y时，台站1、台站2以及飞机在同一个垂直于地面的90°圆弧面上，无法形成定位所需的相交垂线，误差为无限大，即无法定位。

仿真条件2：假设台站1的位置为(0，0，0)，台站2的位置为(1 km，-1 km，0)，方位测量误差ε1=ε2∈[0.5，2]，飞机位置(2 km，2.5 km)。塔康双站定位的定位误差随方位测量误差的变化关系如图5所示，方位测量误差范围取0.5°～2°，步进取0.1°。

由仿真结果可知，无论是以台站1还是以台站2为顶点计算定位误差，随着方位测量误差的增大，定位误差相应增大。由于本仿真中台站2与飞机位置的距离更小，故利用台站2为顶点计算的误差相应更小。

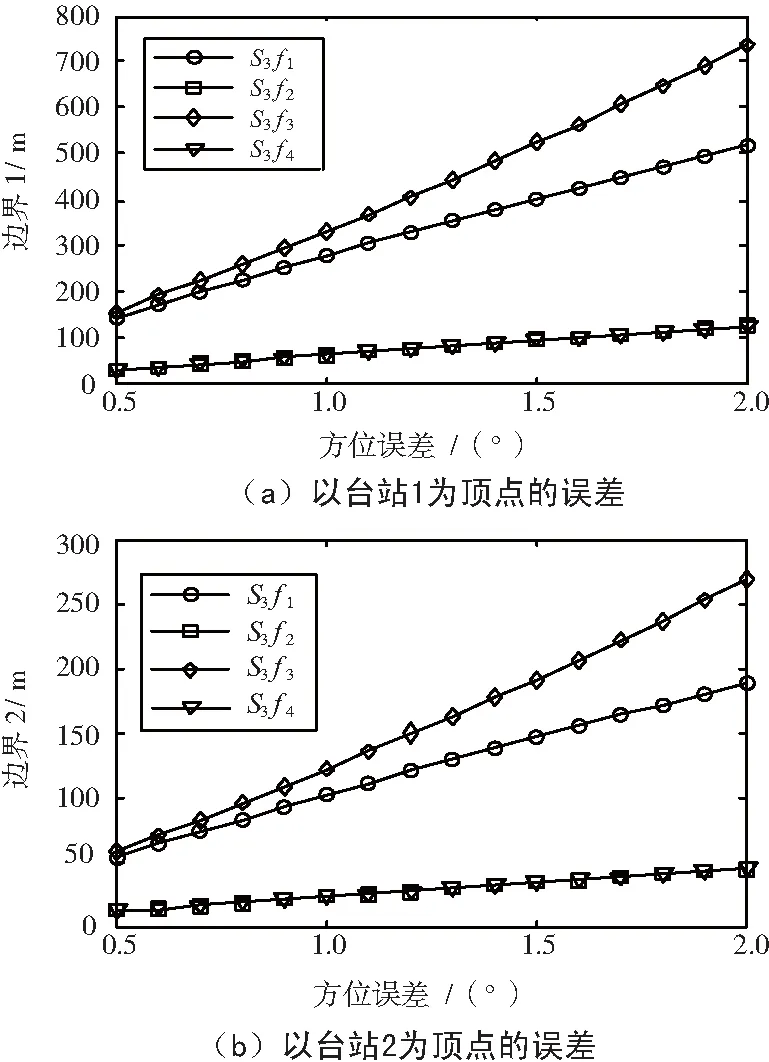
图5 定位误差与方位测量误差的关系

4 结束语

塔康无源定位技术是可行的，但定位精度受方位测量误差、台站位置等多方面因素影响，随着方位测量误差的增大，定位误差相应增大。下一步的研究重点将是在全机航电系统下，机载设备提供诸如伏尔或惯导等其他辅助信息作数据融合处理，同时需要解决多站之间的数据同步问题，可进一步提高塔康无源定位的精度并将其应用于实际工程中。