量子粒子群BP神经网络在GNSS高程转换中的应用分析

(宁波市测绘设计研究院，浙江 宁波 315100)

GNSS技术不断完善和成熟，其在测绘领域的应用也变得越来越广泛，大幅提高了测绘外业工作效率，但在大地高与水准高转换应用方面仍主要依赖水准面精化模型[1]。通过水准面精化模型进行高程转换，优点是精度高；缺点是建设成本大、周期长，对作业人员技术水平能力要求高，大范围推广应用难度较大。在经费少、工期短、范围小、无法使用水准面精化模型的情况下，如何高效、便捷地实现GNSS高程转换，已经成为制约GNSS高程应用的一个难题。

目前主流的GNSS高程转换方法就是利用获取的样本数据，通过严密的数学计算方法，建立GNSS点坐标与水准高之间的数学映射关系模型。BP神经网络算法是一种模拟人脑的数学计算方法[2-3]，具有网络自适应映射能力，可用于GNSS高程转换的非线性映射运算，但其本身也存在一些缺陷，主要表现为收敛缓慢，易出现因“过训练/过拟合”情况而陷入局部最优，网络参数确定困难等。

量子粒子群算法(quantum-behaved particle swarm optimization，QPSO)是一种引入了量子行为的启发式进化算法，具有极强的粒子搜索性能，使粒子可以在空间中更高效地搜索到全局最优解，目前已被广泛应用于函数优化、神经网络训练等领域。

本文提出利用量子粒子群算法(QPSO)对BP神经网络进行优化，通过构建量子粒子群BP神经网络实现GNSS点坐标到正常高的转换计算，改进传统BP神经网络算法存在的局部收敛、无法收敛等缺陷，并通过仿真试验来验证量子粒子群BP神经网络算法的实际效果。

1 粒子群优化算法(PSO)

粒子群优化算法是一种随机全局迭代进化算法[4-6]，具有稳健性和全局搜索能力强、参数少、算法简单、易编程实现等优点，能有效改进BP神经网络易陷入局部最优的缺陷，大大提高其计算效率及性能。

PSO算法通过搜索空间中粒子位置求取优化问题最优解，算法具体原理如下：

假设存在一个D维搜索空间，该空间中有S个粒子组成的粒子群X={X1，X2，…，Xs}，根据适应度函数计算并寻找最优解。第i个粒子的位置在搜索空间中可表示为向量Xi=[Xi1Xi2…Xid…XiD]T，速度可表示为向量Vi=[Vi1Vi2…Vid…ViD]T，个体最优解可表示为Pi=[Pi1Pi2…Pid…PiD]T，整体最优解可表示为Pg=[Pg1Pg2…Pgd…PgD]T。通过粒子自身速度和位置的不断迭代，对当前解Xi、个体最优解Pi、整体最优解Pg适应度值进行比较，不断更新个体最优解Pi及整体最优解Pg。每进行一次迭代，粒子会通过式(1)更新自身位置和速度，即

(1)

式中，d=1，2，…，D；i=1，2，…，S；k为迭代次数；Vid为粒子速度；c1和c2分别为认知学习因子和社会学习因子，表示寻找最优解的加速项权重；r1和r2为分布于[0，1]区间的随机数；w为惯性权重，主要控制算法搜索和收敛能力。当w取值较大时，算法全局搜索能力强而局部收敛性弱；当w取值较小时，算法局部收敛性好但全局搜索能力弱。

粒子位置和速度一般限定在区间[-Xmax，Xmax]和[-Vmax，Vmax]内，Xmax限定粒子位置区间，Vmax限定粒子最大移动距离，以防止粒子盲目搜索、提高算法收敛性；w初始值通常取较大值，令其随着粒子群迭代而线性递减，保证算法在迭代初期具有较强的全局搜索能力，而在后期则转向局部精细搜索以获得高精度最优解。

2 量子粒子群算法(QPSO)

经典力学中，粒子i沿确定轨迹运动，其状态由位置Xid和速度Vid来确定；但在量子力学中，粒子行为则具有多态和不确定性，有概率出现在空间任一位置，其位置Xid和速度Vid无法同时确定。因此，如果粒子具有量子行为，则PSO算法的工作方式将变得不同，即孙俊等提出的粒子具有量子行为的QPSO算法[7]，其算法具体原理如下：

假设一个D维搜索空间中有m个粒子组成的粒子群，记第i个粒子当前位置是Xi=[Xi1Xi2…Xid…XiD]T，第i个粒子搜索到的最优位置为Pi=[Pi1Pi2…Pid…PiD]T，粒子群整体最优位置为Pg=[Pg1Pg2…Pgd…PgD]T，势中心点P=[P1P2…Pd…PD]T。其中势中心点计算公式为

Pd=(r1Pid+r2Pgd)/(r1+r2)

(2)

粒子状态则按下式进行迭代和更新

L=z|Xid(t)-P|

(3)

(4)

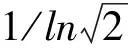
3 量子粒子群BP神经网络方法及实现

QPSO算法优化BP神经网络的基本原理如下：将神经网络权值和阈值进行粒子化，根据网络结构定义并构建粒子群空间，其空间维数D一般由网络输入层节点数n、隐含层节点数l、输出层节点数m来确定，具体可表示为D=n×l+l×m+l+m。搜索空间中的每个粒子代表着神经网络的一组权值和阈值，通过QPSO算法的不断迭代和搜索，使粒子适应度值在终止条件下趋于最小，从而寻找到粒子最优位置向量，即为BP神经网络的最优权值和阈值，可用于神经网络的拟合计算，提高收敛效率和精度。量子粒子群BP神经网络算法基本流程如图1所示。

量子粒子群BP神经网络算法具体实现方法及步骤如下：

(1) 初始化粒子群参数，包括粒子位置(粒子位置即为待优化网络权值和阈值)、寻优范围、压缩扩张因子、迭代次数等。

(2) 计算种群中每个粒子适应度值，获取每个粒子的个体最优位置和粒子群的全局最优位置。

(3) 根据群体中各粒子的个体最优位置计算平均点。

(4) 通过迭代寻优对群体中每个粒子的位置进行更新。

(5) 重复步骤(2)—(4)，直至达到终止条件。

(6) 输出粒子群全局最优解，作为优化后的网络最优权值和阈值，进行数据计算及分析。

本文将QPSO-BP神经网络算法的适应度函数定义为

(5)

式中，RMSE为均方根误差，代表预测数据与真实数据间的偏离程度；θ=1,2，…，L，L为训练样本数量；z(θ)和z*(θ)分别表示真实数据和预测数据。

4 试验分析

本文选取某市40个GNSS控制点成果数据(X，Y，h)作为样本进行仿真试验，以控制点坐标成果X、Y作为2个输入神经元，控制点水准高h作为1个输出神经元，隐含层设置为7个神经元[8-9]，其中25个样本数据进行QPSO-BP神经网络算法优化与训练，其余15个样本数据进行数据计算与分析。

仿真试验中分别使用PSO算法、QPSO算法对BP神经网络进行了优化。其中，PSO算法参数设置为[10-12]粒子数20，c1=c2，w=0.9，迭代次数500次；QPSO算法参数设置为粒子数20，迭代次数500次，z=0.8。

通过PSO算法、QPSO算法对BP神经网络进行优化后，可得到其网络模型的29个最优权值和阈值。由于篇幅有限，本文仅给出QPSO算法优化得到的最优解，见表1。

表1 QPSO算法优化得到的最优权值和阈值

根据优化后得到的最优权值和阈值，分别构建PSO-BP神经网络、QPSO-BP神经网络，利用25组样本数据进行网络训练，再使用训练后的神经网络模型对剩余15组样本数据进行数学模拟计算[13]。由于篇幅有限，这里只给出QPSO-BP神经网络的最终拟合及预测情况，见表2、表3。

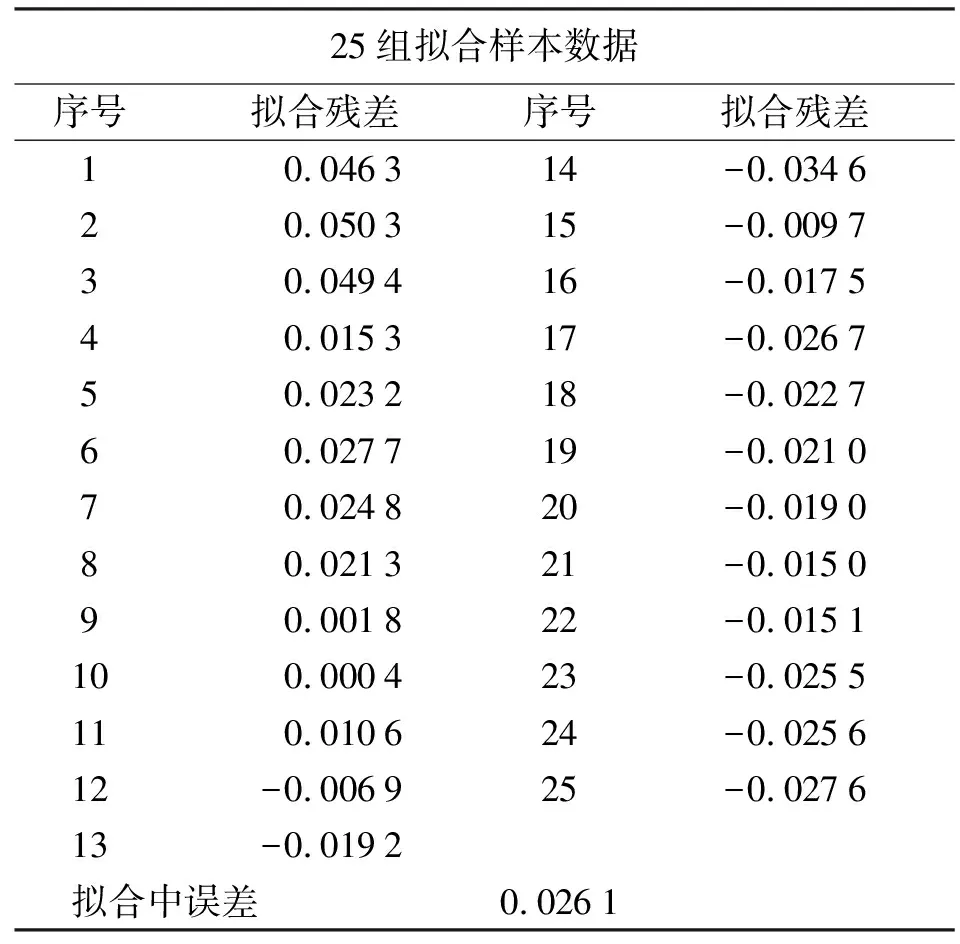
表2 QPSO-BP神经网络拟合情况 m

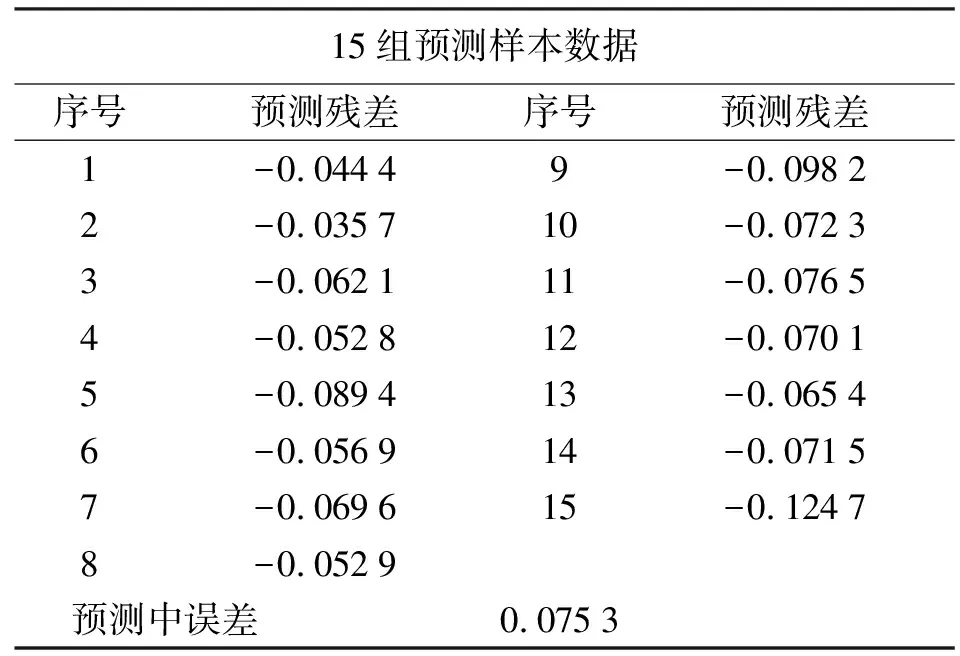
表3 QPSO-BP神经网络预测情况 m

为了更好地验证QPSO算法对BP神经网络的优化效果，本文分别对BP神经网络、PSO-BP神经网络、QPSO-BP神经网络的拟合和预测结果进行了比较分析，具体结果见表4、图2、图3。

根据上述比较分析结果可以看出：利用量子粒子群(QPSO)算法优秀的迭代进化性能和全局搜索能力[14-15]，可实现对BP神经网络的有效优化，快速跳出局部最小而趋于全局最优解，最大限度避免BP神经网络收敛慢、易陷入局部最小、难以收敛到全局最优解的缺陷，大大提高GNSS高程转换的效率、精度和可靠性。

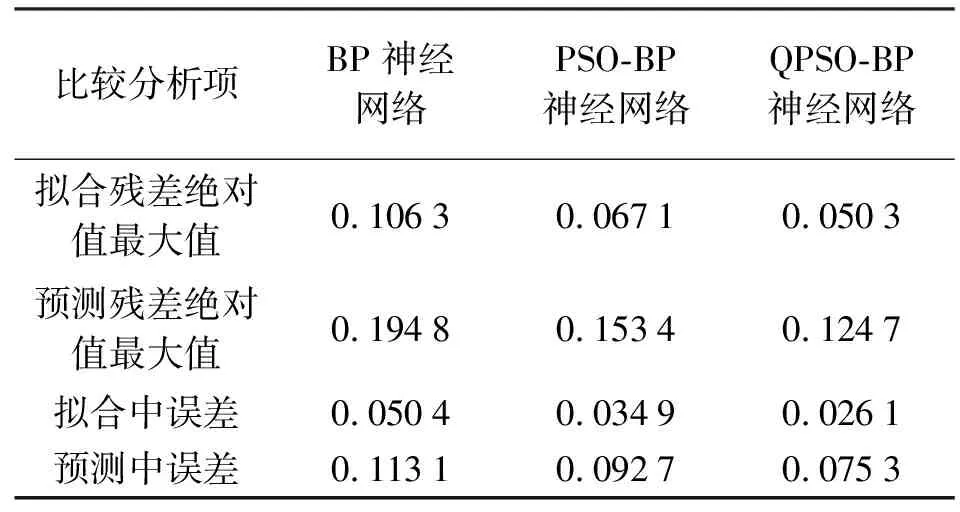
表4 BP、PSO-BP、QPSO-BP 3种算法仿真结果比较m

QPSO-BP算法在数据拟合、预测方面的精度和可靠性均优于BP模型、PSO-BP模型，是一种更加优秀的数学模型，在GNSS高程转换应用方面具有较大的推广应用潜力。

5 结 语

本文提出了一种基于量子粒子群BP神经网络算法的GNSS高程转换数学模型，利用量子粒子群算法的全局迭代进化特性搜索获取BP神经网络最优权值及阈值，有效解决了传统BP神经网络算法极易陷入局部极值、无法收敛到全局最优解等缺陷，在GNSS高程转换方面表现出了更高的效率、精度和可靠性，是一种更加快速、高效的数学模型，值得在GNSS高程转换方面进行推广应用。