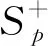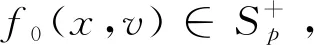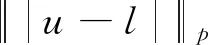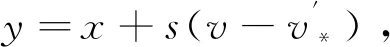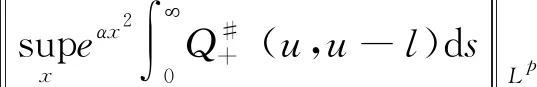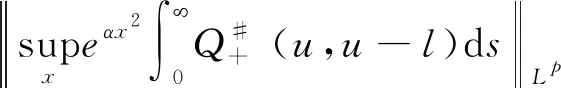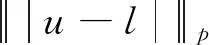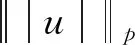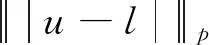Boltzmann方程在不同位势下温和解的存在性和唯一性
孟 飞
(南京邮电大学 理学院,江苏 南京 210023)
引 言
Boltzmann方程是统计物理中的一个重要的方程,以下面的形式给出:
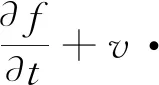
(1)
其中,未知函数f表示稀薄气体的分布函数,一般依赖于变量x,v,t,它的物理意义是:对于任意的时间t,在x与x+dx的体积元内,速度在v与v+dv之间的分子数。这个方程主要描述了在非平衡状态下,稀薄气体的分布函数f关于时间t演化的过程。方程中的对流项v·xf描述了分子本身的运动,而碰撞算子Q(f,f)刻画了分子间的碰撞,它的具体形式如下:
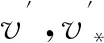
它们满足下面的动量及能量守恒关系式:
.
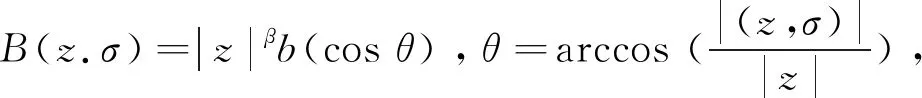
显然此时b(cosθ)在球面上是不可积的,这给方程的研究带来了很大的困难。因此在很长的一段时间里,数学家所作的工作都是基于这么一个条件:

这个条件被称为角截断条件,在这个条件下,碰撞算子可以分成两部分,即
Q(f,f)=Q+(f,f)-Q-(f,f),
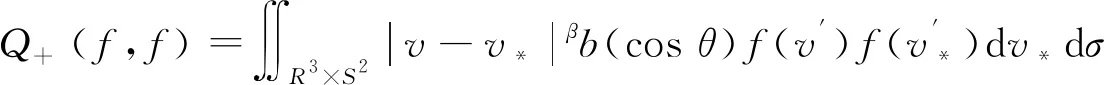
Q-(f,f)=∬R3×S2|v-v*|βb(cosθ)f(v)f(v*)dv*dσ
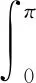
除此之外,经过数学家们的研究,碰撞核的参数β也对解的性质有很大的影响,其相应的分类如下:
若β<0,称为软势;
若β=0,称为麦克斯韦势;
若0<β1,称为硬势,特别的若β=1,称为刚球。
对于Boltzmann方程研究的困难主要在于两个方面,一是对流项和碰撞算子同时出现在方程中;二是碰撞算子中复杂的结构。近年来,关于Boltzmann方程的研究取得了很多进展,很多重要的问题已经得到了解决。下面我们主要回顾温和解,重整化解以及平衡态附近的解这三个方面的相关结果。
在角截断情形下,Kaniel和Shinbrot[1]首先在一个空间有界的区域内发明了一种迭代技术证明了局部温和解的存在性。不久,Illner和Shinbrot[2]利用这种技术在刚球情形下进一步证明了整体温和解的存在性,但此时初值需要关于变量x满足指数衰减。这种方法深深的影响了上世纪80年代的Boltzmann方程的研究工作,Bellomo,Toscani[3,4,5]进一步将这种技术推广到不同的初值以及不同的碰撞核中。而Ha[6]讨论了这类解的稳定性。2009年,Alonso和Gamba[7]在初值关于变量x和v同时呈现指数衰减时,系统的研究了温和解的存在性及正则性,稳定性等性质。最近,温和解的理论由Boltzmann方程延伸到描述颗粒物质的非弹性Boltzmann方程中,Alonso[8]用类似于文献[1]中的做法证明了非弹性Boltzmann方程温和解的存在性,而Wei和Zhang[9]则探讨了在外力条件下非弹性Boltzmann方程温和解的存在性和稳定性。
由于温和解对初值所处的函数空间有较强的限制,Boltzmann方程的重整化解是由Diperna和Lions于80年代末开创性提出的。1989年,Diperna和Lions[10]首先在角截断条件下给出了重整化解的存在性,他们的证明基于Boltzmann方程的重整化形式及L1空间的弱紧性。随后Diperna和Lions[11]进一步深入讨论了上述解的性质:建立了熵不等式。如何将重整化解推广到非角截断条件,这个问题一直到2003年才由Alexandre和Villani[12]解决。但是关于此类解的很多问题都没有得到解决,如解的唯一性,解的能量是否守恒等。
而对于Boltzmann方程在平衡态附近的解,Guo[13]在2003年证明了在角截断及软势条件下经典解的存在性,他的方法主要基于高阶导数的能量估计和碰撞算子的线性化理论,文章也指出其方法也可以适用于硬势条件。不久,Alexandre,Morimoto,Ukai,Xu和Yang[14,15,16,17]在非角截断条件下做了一系列的工作,他们利用能量方法和碰撞算子的线性化理论研究了不同的位势下解的重要的性质,包括存在性,唯一性,正则性等。与角截断条件下结论不同地方在于此时的解具有正则化效果:即在任意时刻,解都会变得光滑。
预备知识及主要结果
1.1 温和解
我们首先介绍下本文所用的函数空间及相关的范数,对于任意的p>1,定义函数空间Sp如下:
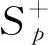
其次介绍本文需要研究的温和解的概念,首先定义迹算子
f#(x,v,t):=f(x+vt,v,t),Q#(f,f)(x,v,t):=Q#(f,f)(x+vt,v,t).
对方程(1)沿着输运算子∂t+v·x的特征线方向积分,就可以得到如下方程:
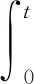
(2)
其中f0(x,v)表示初值,利用方程(2),我们给出温和解的定义:
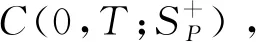
注:如果f关于变量x和t是光滑的,那么方程(1)的解和方程(2)的解是等价的。因此,方程(2)可以是认为是方程(1)的一种弱形式。
1.2 本文的主要结论及方法
本文主要将Illner和Shinbrot在文献[2]中关于温和解的存在性的结果由刚球模型推广到其他位势中,得到了温和解的存在性和唯一性。主要想法是利用Kaniel和Shinbrot在[1]中使用的迭代技术来证明,但与刚球模型不同的是,在计算过程中,为了估计奇异积分,我们将使用碰撞算子在软势情形下的Lp估计,这也是我们在1.1节引入了新的函数空间Sp的原因。我们的结果表明此时初始值所在的空间Sp依赖于碰撞核中的参数β。
2 迭代技术
这部分主要介绍下Kaniel和Shinbrot[2]使用的迭代技术,考虑下面的两个方程:
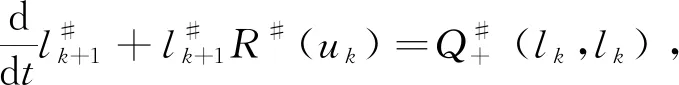
(3)
(4)
lk+1(0)=uk+1(0)=f0(x.v).
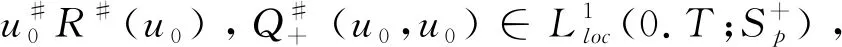
lk-1(t)lk(t)uk(t)uk-1(t),
那么
lk(t)lk+1(t)uk+1(t)uk(t)
也成立。
利用数学归纳法可知,如果条件
l0(t)l1(t)u1(t)u0(t),
(5)
因为函数列{lk}和{uk}具有单调性,故可设{lk(t)}的极限为l(t),{uk(t)}的极限为u(t),对方程(3)和(4)两边同时积分并利用控制收敛定理可得
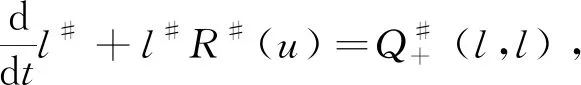
(6)
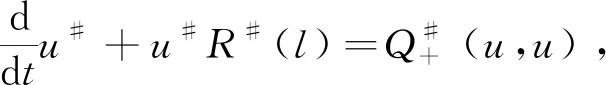
(7)
显然如果能证明u(t)=l(t),那么f:=u=l即为Boltzmann方程的温和解。
下面我们主要研究初始条件(5),若令l0=0,由方程(3)和(4)容易得到0=l0(t)l1(t)u1(t),此时开始条件(5)就退化为u1(t)u0(t),因此我们可以得到下面的引理:
引理1对于任意的0t 在这一部分中,我们将构造一个函数u0(t,x,v),使得条件u1(t)u0(t)成立。首先令如果l0=0,则通过方程(4),可知 因为 (8) 上述条件又等价于 根据文献[2]中的结果可知 因此只需要找到一个函数,使其满足积分方程 我们发现如果β<1,那么上面的积分是一个奇异积分,定义下面的积分算子T: 首先我们验证这个算子是一个Lp(R3)→Lp(R3)的有界算子,其中参数p待定。 我们发现对上方不等式右边第二项的估计其实是对碰撞算子Q+在软势情形下的Lp估计,为此我们需要文献[18]中的一个的引理。 引理2对于任意的1 那么有 这里Cb表示一个依赖于b(cosθ)的常数。 利用引理2,则 上面的不等式表明如果Cb,α·2R1,那么这个映射就是的压缩映射,我们就可以应用不动点定理找到这样的ω。若要满足不等式 只需要选择适当的R,使得下式 证明首先我们证明第三部分中u(t)=l(t)即是Boltzmann方程的温和解,定义范数如下: 所控制,应用在第三部分中关于时间的积分: 我们有 再次利用引理2及第三部分中的结果对上式右端进行估计。 容易证明其他三项的估计与第一项的估计类似,综合这四项的估计,我们有 又因为 则 而对于温和解的唯一性,假设对于同一个初值f0(x,v)有两个不同的温和解f和g,我们利用证明u=l的步骤即可得。3 初始条件
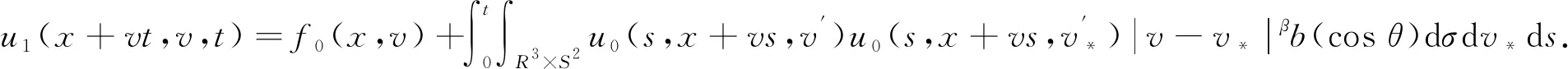
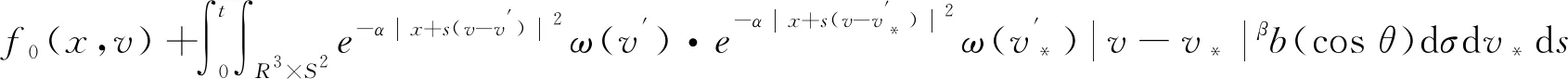
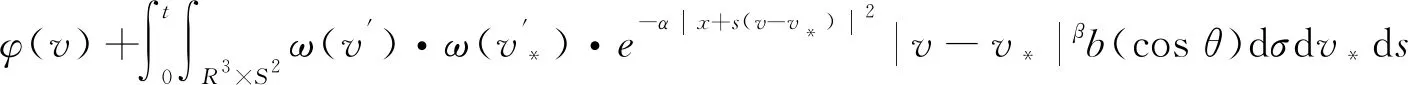
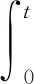
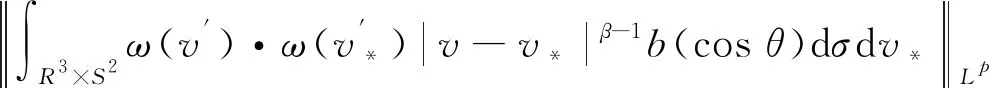
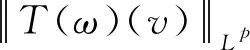
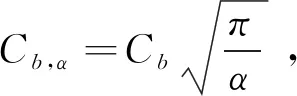
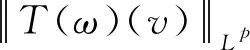
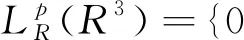
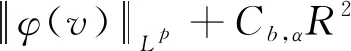
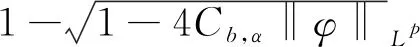
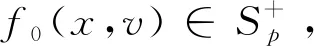
4 存在性和唯一性