基于脉冲压缩的宽带数字接收机设计

陈 涛，蔡兴鹏，潘大鹏

(哈尔滨工程大学信息与通信工程学院，哈尔滨 150001)

目前宽带数字接收机已经被广泛应用到雷达、通信等领域，在电子战中有着不可或缺的重要地位[1].但是随着电子侦察面临的电磁环境的日益复杂，现代电子战中截获的雷达信号为了提高自己的战场生存能力往往处在信噪比很低的环境，并且多数采用低截获概率(low probability of intercept，LPI)雷达信号[2]，对目前电子侦察系统普遍采用的传统数字接收机提出了挑战．传统数字接收机大部分采用 FFT测频和相位差测频[3]，很难处理信噪比 0dB以下的信号，并且大多采用均匀信道化结构，即一旦信道划分后，信道宽度就不可改变，针对大带宽雷达信号会产生严重的跨信道问题，导致信号判别出现错误，增加了后续信号检测与识别处理的难度[4]．

针对上述传统数字接收机所面临的亟待解决的问题，经典的脉冲压缩理论在模拟域给出了解决方案．Klauder在 1960年发现脉冲压缩系统可以用于傅里叶变换，从而打开了压缩接收机研究的大门[5].压缩接收机不仅可以处理多个同时到达信号而且可以对噪声进行很大程度上的压制，是实现低信噪比下信号接收、处理的重要方法[6]．而压缩接收机本身结构则决定了它不存在传统数字接收机的跨信道问题.

文献[7]分析了压缩接收机对同时多目标信号输入的处理能力，但是不够全面，只给出了部分的理论推导．文献[8]讨论了主要影响压缩接收机脉冲压缩性能的几个因素．文献[5]提出了压缩接收机在低信噪比下的测频方法，但是没有给出输入信号的载频约束，所讨论的信号输入时刻情况也不完整．文献[9]提出了压缩接收机接收雷达信号的方法．上述所有文献所讨论的均为压缩接收机在模拟域下的情况，并不适用于构造新型数字宽带接收机．文献[10]则提出了一种基于压缩感知理论的 MWC结构新型数字宽带接收机，通过将信号与伪随机序列进行混频至基频后抽取，实现了欠奈奎斯特采样，但是在低信噪比下对信号的处理能力不足．

基于上述研究，本文在文献[5，7，10]的研究基础上以脉冲压缩理论为依据，将输入信号与线性调频信号混频，构建了新型宽带数字接收机．将压缩接收机从模拟域扩展到离散数字域，用于现代电子战中；推导了被动宽带雷达信号经过数字压缩接收机后输出信号的离散模型；给出了不同情况下数字压缩接收机的测频方法；给出了被动雷达信号带宽、脉宽、幅度等脉冲描述字(PDW)参数的测量方法；最后通过仿真逐一对设计的有效性进行了验证．

1 数字机压缩接收机结构构建

1.1 数字压缩接收机结构

从工作原理上讲，压缩接收机是建立在一种特殊的线性调频傅里叶变换的基础上实现的．这种特殊的傅里叶变换又被称作Chrip变换[11]．离散Chrip变换算法模型可以概括为：M-C-(M)．其中，M 代表乘法，C代表卷积．因为在大多数应用中对相位谱不做要求，因此可以舍去最后的乘法模块，将结构简化为一次乘法运算和一次卷积运算[12]．

图 1为根据离散 Chrip原理给出的数字压缩接收机的基本结构框图．信号经过AD采样后得到离散数字信号进入混频模块和线性扫频本振进行混频得到混频后信号，将混频信号和数字延迟模块中的带通滤波器进行卷积运算即可将脉冲进行压缩得到输出的脉冲尖峰，通过检波器对脉冲尖峰的峰值和位置进行测量，可以通过后续计算得到信号的PDW信息．

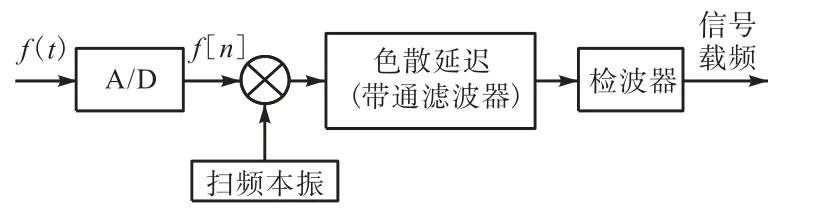
图1 数字压缩接收机结构Fig.1 Digital compressive receiver structure diagram

1.2 输出信号的离散形式推导

针对图1中给出的数字压缩接收机，给出离散信号经过数字压缩接收机后的离散数字域输出信号形式．整个数字压缩接收机模型的推导过程是建立在输入复数信号的情况下完成的．

设经过AD采样后的离散化输入信号为

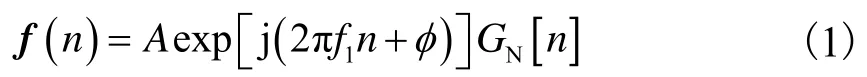
式中：A为信号的幅度；f1为信号的载频；为信号初相；]为矩形函数，当时取值为1，当对雷达的脉内参数进行分析时，在整个推导过程中取值为1．

设本振扫频信号为

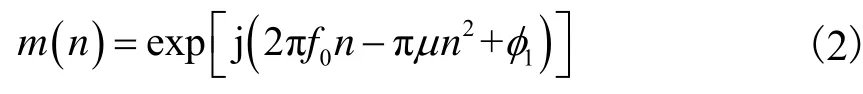
式中：f0为扫频信号初频；为扫频信号的调频斜率；为扫频信号初相．

则混频输出信号为

设带通滤波器的单位冲激响应为

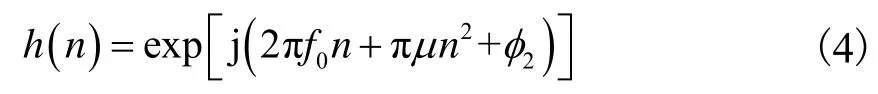
式中f2为滤波器阶跃响应初相．

则数字压缩接收机的输出为

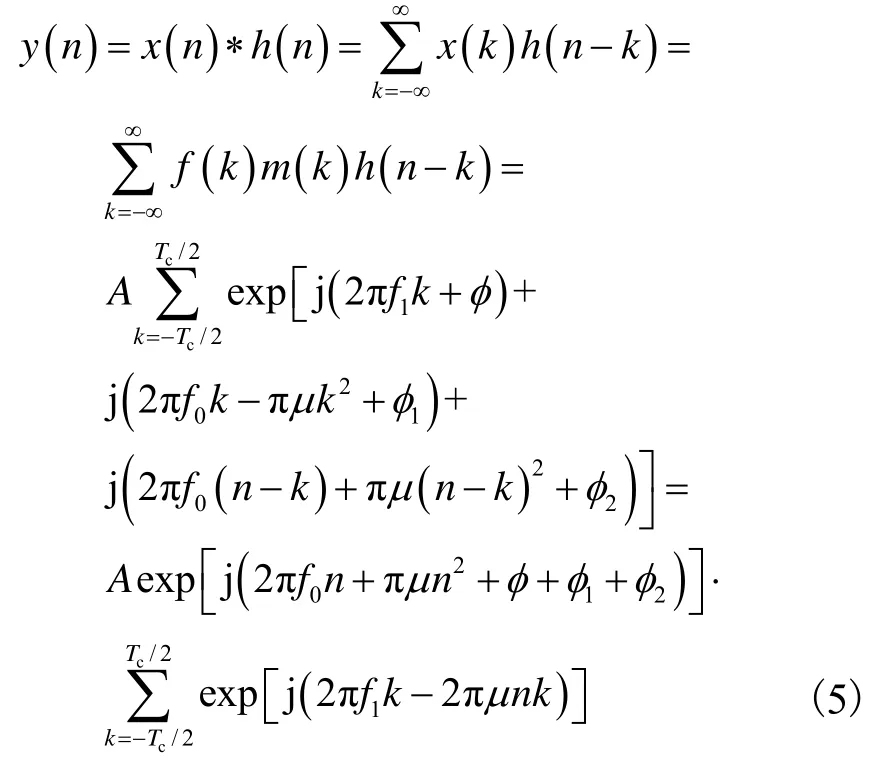
式中Tc为混频后信号的脉宽．

根据等比数列求和公式可得式(5)等价于

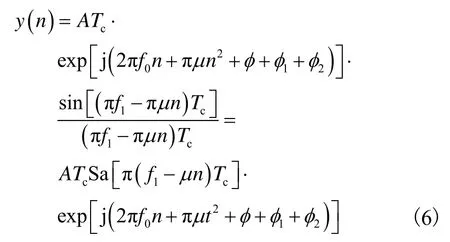
式(6)即为采样后信号通过压缩接收机后输出信号的离散数字形式．

根据式(6)不难看出，输入信号经过数字压缩接收机后压缩成一个包络为抽样函数的复数信号输出，并且发现，输入信号的载频f1只与输出复数信号的包络有关．根据抽样函数的性质可知，当抽样函数的自变量取 0时，整个抽样函数取值达到最大为 1．即信号的包络会在的时刻取得最大值．因此，只需要找到信号包络的最大值点所对应的采样点，即可以求出信号的输入频率．

2 压缩接收机PDW测量

2.1 输入信号载频约束条件

如图2所示，常规雷达信号经过和本振信号混频后变成了一个带宽和本振信号相同的线性调频信号，然后和带通滤波器进行卷积运算．如果带通滤波器的带宽不够，不足以将整个混频后信号滤出，则信号的能量会有所损失，输出的脉冲尖峰的高度会有所下降，信息会有所丢失．为此给出了输入信号载频与本振信号和带通滤波器信号的带宽之间的关系．

图2 数字压缩接收机频谱Fig.2 Spectrogram of digital compressive receiver

设信号载频为f1，扫频信号的初频为f0，带宽为扫频信号的调频斜率，为正向扫频过程．数字延迟信号的初频为f0，带宽为，为负向扫频过程．其中pw1、pw2分别为扫频信号和带通滤波器信号的宽度．

则扫频信号的扫频范围为；带通滤波器的频率范围为；混频信号频率范围为．

可以推出输入信号载频与本振信号和带通滤波器的带宽有如下的关系．

(1) 混频信号频率范围与带通滤波器频率范围有交集的最低约束

(2) 带通滤波器频率范围包含混频信号频率范围的满能量约束

只要输入信号的频率满足最低约束就可以压缩出能量完全或者有缺失的脉冲尖峰，而且无论何种情况压缩出的脉冲尖峰都含有全部的载频信息，因此对于只需要载频信息的信号而言，输入信号载频满足最低约束即可．

2.2 输入信号载频测量

第 1.2节所提到的测频方法为输入信号和扫频信号在扫频起始点进行混频．但还有一种更为普遍的情况则是信号在扫频的过程中与扫频信号进行混频，此时由于信号并非在扫频起始点与扫频信号进行混频，因此有一个时间延迟需要进行补偿，才可以求出真正的信号频率．下面给出信号在两种情况下通用的测量载频的公式．

式中：nmax为输出信号包络最大值所对应的采样点；n0为信号从扫频开始到与扫频信号开始混频所经过的采样点数．

2.3 输入信号脉宽、幅度和带宽测量

2.3.1 输入信号脉宽、幅度测量

由式(6)可知信号经过数字压缩接收机输出的复数信号包络峰值与信号的幅度和脉宽均有关，因此只靠一次扫频无法对输入信号的脉宽和幅度进行正确测量．

通过图 1不难发现输入信号与扫频本振混频的过程是一个点乘的过程，因此如果信号经历了一次完整的扫频周期，则其在这次完整的扫频周期中的脉宽就等于扫频本振信号一个周期内的宽度．因此可以以一次完整的扫频周期压缩出的脉冲尖峰峰值为参考，将其余扫频周期内压缩形成的脉冲尖峰峰值与其做比，得到相应的比例系数．将比例系数乘以扫频本振信号一个周期内的宽度则可得到对应扫频周期内的信号脉宽，将所有的扫频周期内的信号脉宽相加即可得到输入信号的真正脉宽．

同理可以利用数字压缩接收机输出的脉冲尖峰峰值来进行输入信号幅度的计算．当信号经历了一次完整的扫频周期时，该扫频周期输出的脉冲尖峰峰值只与信号的幅度和脉宽有关，而一个完整扫频周期的信号脉宽等于本振扫频信号一个扫频周期的宽度，因此，只需要将完整扫频周期输出的脉冲尖峰峰值除以该周期内信号的脉宽即可以求出输入信号的幅度.

信号的脉宽PW和幅度AMP公式分别为

式中：TI为一次完整扫频周期的扫频信号宽度；iA为每个扫频周期的脉冲尖峰峰值；IA为一次完整扫频周期的脉冲尖峰峰值；N为扫频次数．

从式(10)和式(11)中可以看出，对于数字压缩接收机而言，如果想要求取输入信号的脉宽信息则要求输入信号的脉宽必须大于等于 2倍的一次完整扫频周期的扫频信号宽度．

2.3.2 输入信号带宽测量

因为线性调频(linear frequency modulation，LFM)信号的载频随着时间不断地变化，因此 LFM信号经过数字压缩接收机后会被压缩成一个有一定宽度的脉冲输出．根据式(9)可知，每一个脉冲点对应输入LFM信号相应点的输入频率．

因为压缩出来的脉冲幅度明显高于旁瓣噪声幅度，因此，可以选取脉冲幅度最大值的 1/2作为阈值进行脉冲提取，将高于阈值的脉冲提取出来后分别找到最小和最大的采样点数，根据式(9)求出对应频率，并相减即可求出输入LFM信号的带宽．

3 仿真验证

图3为文献[13]所提出的16通道多相滤波结构数字信道化接收机的幅度输出波形．输入信号为采样频率为2 GHz，脉宽为5s，载频960 MHz的单载频信号．从图 3中可以看到，当输入信号的信噪比为8 dB的时候，脉冲两侧已经有很多幅度超过门限与脉冲高度相符的噪声，导致后续脉冲提取以及测频出现错误．

设数字压缩接收机的本振扫频信号的初频为700 MHz，带宽500 MHz，宽度为5s；带通滤波器的初频为700 MHz，带宽为1GHz，宽度为10s．后续仿真如无特殊说明，数字接收机的结构参数不变.信号采用和图 3相同的信号．图 4为数字压缩接收机的幅度输出波形．从图 4中可以看出，压缩出来的脉冲尖峰明显高于两侧噪声，可以正确检测信号．从而验证了数字压缩接收机在低信噪比条件下相比于传统数字信道化接收机具有更强的信号检测能力．

图 5为输入信号在信噪比为29 dB时数字压缩接收机的幅度输出波形．从图 5中可以看出，此时大量噪声幅度已经开始接近压缩出来的脉冲尖峰幅度，信号检测开始出现错误．

3.1 低信噪比下数字压缩接收机信号检测能力

图3 SNR＝-8 dB时传统数字接收机幅度输出波形Fig.3 Output waveform of the conventional receiver under -8 dB SNR

图4 SNR＝-8 dB时数字压缩接收机幅度输出波形Fig.4 Output waveform of the digital compressive receiver under -8 dB SNR

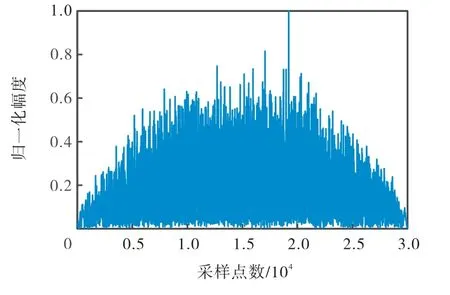
图5 SNR＝-29 dB时数字压缩接收机幅度输出波形Fig.5 Output waveform of the digital compressive receiver under -29 dB SNR

为体现数字压缩接收机的信号检测性能，将1000个信号分为500个纯噪声和500个加入噪声的信号两组，采用不同的信号峰值占比作为阈值进行信号检测并绘制受试者工作特征(receiver operating characteristic，ROC)曲线．图 6为输入信号在信噪比为-29dB时数字压缩接收机检测信号性能的ROC曲线．从图中可以看出，曲线超过正对角线并且接近左上角，证明数字压缩接收机在-29dB的低信噪比下信号检测性能良好．

3.2 数字压缩接收机LFM信号带宽测量

图 7是输入信号为采样频率为2 GHz，脉宽为5μs，信噪比5dB，载频从700 MHz调制到900 MHz的 LFM 信号，数字压缩接收机的幅度输出波形如图7所示．后续仿真如无特殊说明，输入信号的采样频率、脉宽和信噪比不变．

图6 SNR＝-29 dB时数字压缩接收机ROC曲线Fig.6 ROC curve of the digital compressive receiver under -29 dB SNR

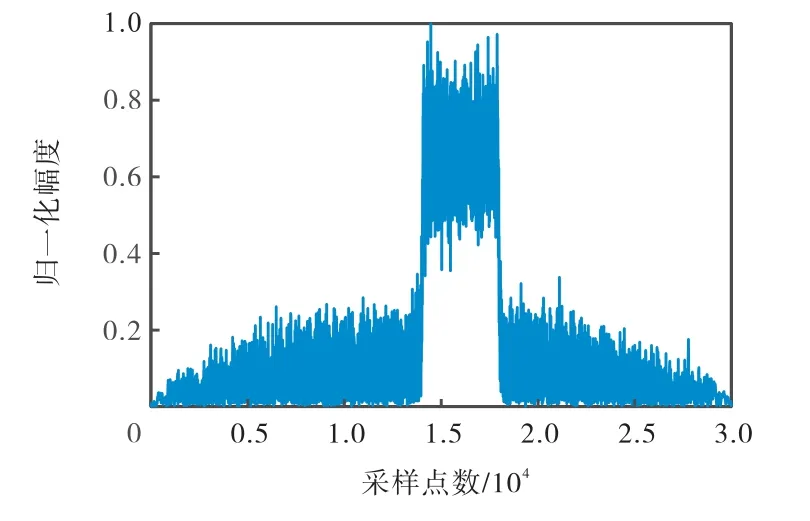
图7 LFM信号输出波形Fig.7 Amplitude of LFM output signals

根据第 2.3.2节所给出的带宽测量方法，计算得到输入LFM信号的带宽为198.85MHz，从而验证了数字压缩接收机测量LFM信号带宽的能力．

图 8给出了在图 7的仿真环境下不同信噪比测得输入LFM信号带宽的均方根误差值，从图 7中可以看出，当信噪比超过5dB以后测得的输入信号带宽的均方根误差小于2 MHz，并且趋于稳定在1.5 MHz，随信噪比提升没有明显下降．从而可以得出，数字压缩接收机测量输入 LFM 信号带宽的最小误差约为1.5 MHz．

图8 不同信噪比下带宽测量误差Fig.8 Error of bandwidth measurement under different SNRs

3.3 数字压缩接收机不同信噪比下的测频能力

前文提到数字压缩接收机可以解决传统多相滤波结构数字信道化接收机在低信噪比下测频能力差的问题，下面对此进行仿真验证．

图 9是在信号载频700 MHz的条件下完成的数字压缩接收机和文献[13]中提出的 16信道传统多相滤波结构数字信道化接收机的测频均方根误差MATLAB仿真实验．信噪比从29 dB步进到5dB，每个信噪比下进行200次蒙特卡洛实验．

从图 9中可以看出传统数字信道化接收机在1 dB 开始测频误差超过1MHz，而数字压缩接收机在信噪比低于-26 dB的时候测频误差才超过1MHz，由此可以看出，数字压缩接收机在低信噪比下处理信号的能力相较于传统数字信道化接收机有着明显的优势．

图9 不同信噪比下两种接收机测频能力Fig.9 Frequency measurement ability of two receivers under different SNRs

3.4 同时到达信号仿真

3.4.1 单载频同时到达信号

在混频开始时输入载频分别为600 MHz和605 MHz的两个同时到达的复数单载频信号，得到数字压缩接收机输出信号的时域波形如图10所示．

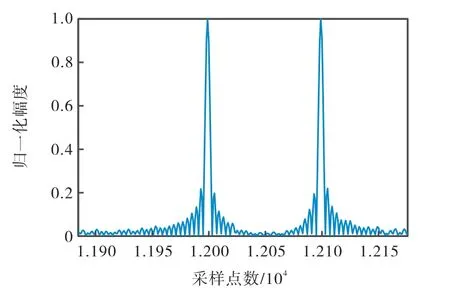
图10 单载频同时到达信号输出时域波形Fig.10 Output time domain chart of simultaneously arrived single-carrier frequency signals

从图 10中可以看出，同时到达的两个单载频信号在输出端被成功地区分开并被压缩成了两个脉冲尖峰输出，根据式(9)计算得到两个脉冲尖峰所对应的载频分别为599.95 MHz和604.95 MHz，验证了数字压缩接收机对同时到达信号的处理能力．

从仿真结果可以看出，数字压缩接收机在5dB下的单载频信号测频分辨率为0.05 MHz，而只要两个信号的载频相差超过数字压缩机的测频分辨率，数字压缩机就可以将两个同时到达的信号区分开并正确测频．

3.4.2 大带宽同时到达信号

传统的信道化结构数字接收机，处理大带宽信号时会产生严重的跨信道问题．而数字压缩接收机因其本身结构特点不存在跨信道问题，而且有着较强的同时到达信号的处理能力．对此本文给出如下仿真．

输入信号为载频分别是 500～700MHz和 0.9～1GHz的两个同时到达的 LFM 信号．在信噪比为5dB的情况下，混频开始时输入，得到数字压缩接收机输出信号的时域波形如图11所示．

从图 11中可以看出，带宽不同的两个线性调频信号经过数字压缩接收机后被压缩成两个宽度不同的独立脉冲输出，从而验证了数字压缩接收机对大带宽同时到达雷达信号的分辨能力．只要大带宽同时到达信号在频谱上没有交叠的情况，数字压缩接收机就可以完成对大带宽同时到达信号的接收和处理．

图11 大带宽同时到达信号输出时域波形Fig.11 Output time domain chart of simultaneously arrived wideband signals

3.5 数字压缩接收机信号脉宽和幅度的测量

设信号的载频600 MHz，脉宽17.5m s，信号幅度为5V；数字宽带接收机的配置和图 4所用相同．在信噪比等于-20 dB条件下将信号在第 1次扫频开始3000点后与扫频信号进行混频，得到数字压缩接收机的输出波形如图12所示．

在图12的仿真条件下，图13和图14为不同信噪比下数字压缩接收机测量信号脉宽和幅度的均方根误差MATLAB仿真实验．信噪比从-29 dB步进到5dB，每个信噪比下进行200次蒙特卡洛实验．

从图 12中可以看出，信号经过了 4次扫频周期，对应压缩出了 4个脉冲尖峰，其中输入信号的载频满足满能量约束条件，并且信号的脉宽满足大于等于2倍一次完整扫频周期的扫频信号脉宽条件，可以进行信号的脉宽和幅度测量．利用式(10)和式(11)计算得到信号的脉宽为17.743μs，幅度为 4.9402V，在误差范围之内．验证了数字压缩接收机在低信噪比下测量信号脉宽和幅度的能力．

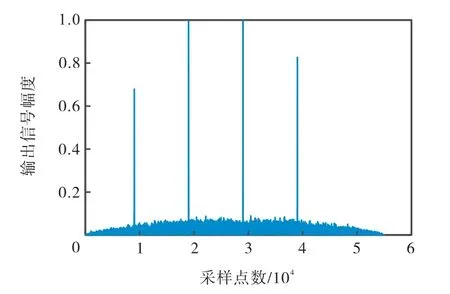
图12 低信噪比多次扫频输出波形Fig.12 Output of multiple sweep signals under low SNR

从图13和图14中可以看出，当信号的信噪比为2 6 dB即测频结果有效的时候，其脉宽测量的均方根误差为0.5s，幅度测量的均方根误差为0.2 V并且随着信噪比的提升不断减小，从而验证了数字压缩接收机在低信噪比下测量信号脉宽和幅度的能力．并且从测量脉宽的原理中可以看出，数字压缩接收机测量脉宽的分辨率和扫频信号的宽度有关．本振扫频信号的宽度越小，数字压缩接收机测量脉宽的分辨率越高．

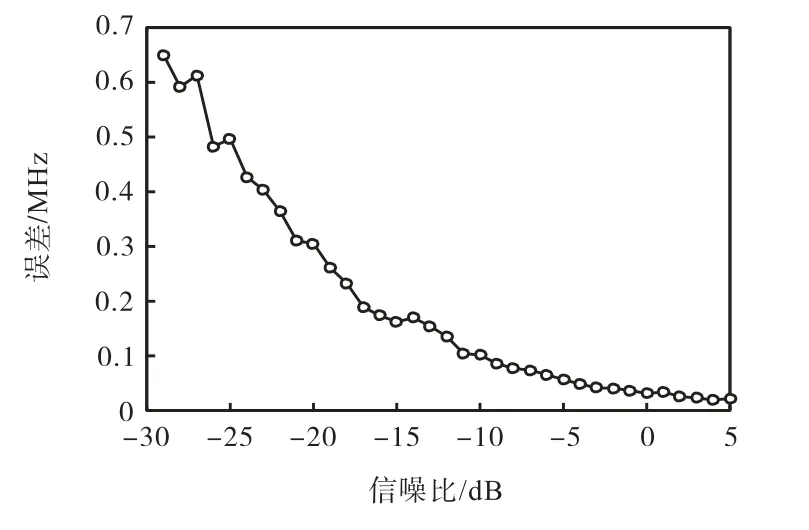
图13 不同信噪比脉宽测量误差Fig.13 Error of pulse width measurement under different SNRs

进一步对扫频信号的宽度对脉宽估计性能的影响进行分析．在相同的仿真条件下，将扫频信号的宽度从1μs以0.5μs步进到10μs，针对每个扫频信号进行200次蒙特卡洛实验计算脉宽的均方根误差，其结果如图15所示．图15中可以看出，随着单次扫频信号宽度的增加即单次脉冲压缩时间的增加，脉冲压缩效果更好，脉宽估计均方根误差逐渐减小．

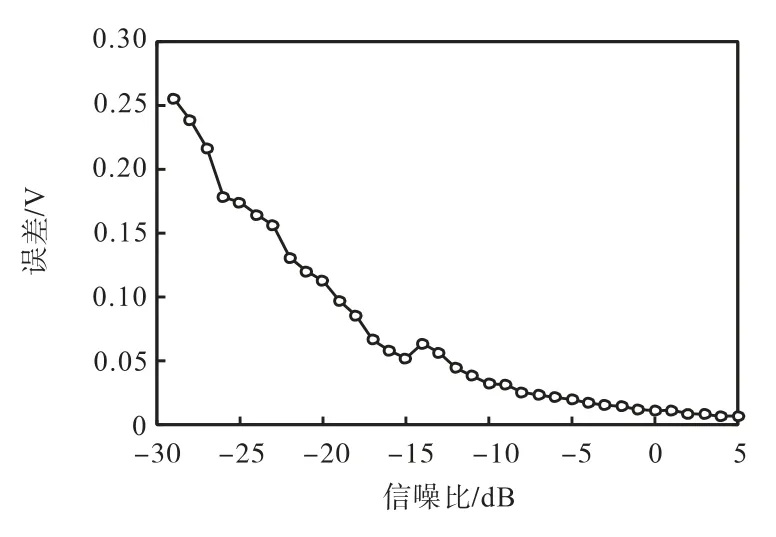
图14 不同信噪比幅度误差Fig.14 Error of amplitude measurement under different SNRs

由此可以看出，对于数字压缩接收机来说，脉宽分辨率和均方根误差无法兼得，具体情况需要根据工程中所制定的指标选取相应的扫频信号宽度．

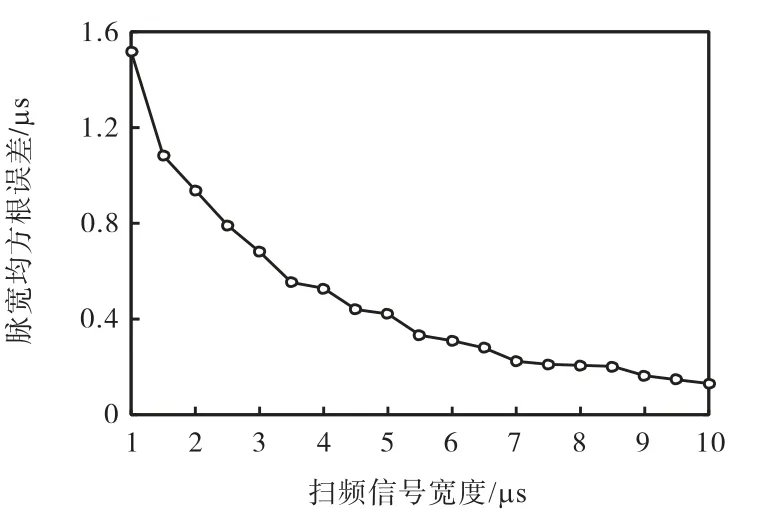
图15 扫频信号宽度对脉宽估计性能的影响Fig.15 Influence of sweep signal width on the performance of pulse width estimation

4 结 语

本文将压缩接收机模型由模拟域推广到离散数字域，提出了新型宽带数字接收机结构的构建．给出了利用数字压缩接收机测量信号 PDW 参数的方法和公式推导．

通过仿真验证了数字压缩接收机处理同时到达大带宽信号的能力；在低信噪比下测频及测量带宽、脉宽和幅度的能力；并对比了传统结构的宽带数字接收机处理低信噪比下信号的能力．通过 ROC曲线验证了数字压缩接收机在低信噪比情况下的信号检测能力，并进一步探讨了不同因素对接收机提取 PDW参数的影响．

本文提出的基于压缩接收机理论的全新结构的宽带数字接收机技术将在实际工程中面对的低信噪比复杂电磁环境中给出新的解决方案，为宽带数字接收机设计提供了新的设计理念，也将为信号侦察与识别提供全新的、更加智能的解决方案，将进一步推动被动雷达的发展．

[1] Coluccia A，Ricci G.About-like detection strategies to combat possible deceptive ECM signals in a network of radars[J].IEEE Transactions on Signal Processing，2015，63(11)：2904-2914.

[2] Huang Ling，Gao Kuangdong，He Zhiming，et al.Cognitive MIMO frequency diverse array radar with high LPI performance[J].International Journal of Antennas and Propagation，2016，2016(5)：1-11.

[3] 司伟建，米胜男，曲志昱，等.数字信道化的调制信号测频方法[J].应用科技，2016，43(3)：28-33.

Si Weijian，Mi Shengnan，Qu Zhiyu，et al.Frequency measurement method of modulated signals based on digital channelization[J].Applied Science and Technology，2016，43(3)：28-33(in Chinese).

[4] 刘小蒙，邵高平，汪 洋，等.基于双门限的动态信道化子带频谱检测方法[J].信息工程大学学报，2017，18(2)：176-180.

Liu Xiaomeng，Shao Gaoping，Wang Yang，et al.Subband spectrum sensing of dynamic channelization based on double thresholds[J].Journal of Information Engineering University，2017，18(2)：176-180(in Chinese).

[5] 王 建. 縮压 接收机的关键技术研究[D].南京：南京理工大学，2013.

Wang Jian.The Research on Key Technology of Compressive Receiver[D].Nanjing：Nanjing University of Science and Technology，2013(in Chinese).

[6] Martin B，Karlheinz K.Position estimation of RFID based sensors using passive SAW compressive receivers[J].Sensors & Actuators A Physical，2016，244：277-284.

[7] 程水英，陈鹏举，武传华.同时多目标信号输入时对压缩接收机的数学分析[J].无线电工程，2000(3)：5-7.

Cheng Shuiying，Chen Pengju，Wu Chuanhua.The mathematical analysis of compressive receivers with simultaneous target signals[J].Radio Engineering，2000(3)：5-7(in Chinese).

[8] 董英英，王启峰.压缩接收机的性能分析[J].仪器仪表用户，2009，16(5)：69-70.

Dong Yingying，Wang Qifeng.The performance analysis of compressive receivers[J].Electronic Instrumentation Customer，2009，16(5)：69-70(in Chinese).

[9] Kawalec A，Pieniezny A.Some results of radar signal detections by the use of compressive receiver[C]// International Conference on Modern Problems of Radio Engineering.Piscataway，NJ，USA，2010：87-88.

[10] Chen Tao，Liu Lizhi，Guo Limin.Wideband signal detection based on MWC discrete compressed sampling structure[J].Transactions of Nanjing University of Aeronautics and Astronautics，2017，34(2)：105-114.

[11] Poisel R A.电子战接收机与接收系统[M].楼才义，等译.北京：电子工业出版社，2016.

Poisel R A.Electronic Warfare Receivers and Receiving Systems[M].Lou Caiyi， et al trans.Beijing：Publishing House of Electronics Industry，2016(in Chinese).

[12] Pieniezny A，Fornalik J.Weak signal detection using compressive receiver[J].Radar Symposium，2010(8)：1-4.

[13] 陈 涛，岳 玮，刘颜琼，等.宽带数字信道化接收机部分信道重构技术[J].哈尔滨工程大学学报，2011，32(12)：1610-1616.

Chen Tao，Yue Wei，Liu Yanqiong，et al.Research on partial channel reconstruction technology based on wideband digital channelized receiver[J].Journal of Harbin Engineering University，2011，32(12)：1610-1616(in Chinese).