海上风电筒型结构基础层状地基参数优化反演

赵 悦 ，练 冲 ，练继建 ，董霄峰 ，王海军

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300350；2.天津大学建筑工程学院，天津 300350)

海上风电作为一种可再生的清洁能源，越来越受到世界各国的重视[1-2]．我国拥有丰富的海上风能资源，“十三五”规划指出到 2020年我国海上风电并网装机容量计划达到 500×104kW．海上风电以其风资源稳定、占用土地少、离沿海地区近等优点成为我国发展可再生清洁能源的重要组成部分[3-4]．

海上风电结构主要包括转子、发电机、机舱组成的上部结构和塔筒、基础组成的支撑结构．统计表明，支撑结构费用约占整个海上风电结构总投资的20%至25%[5]．其中复合筒型基础是一种适用于我国沿海软黏土地基的新型基础形式，以其优越的性能在海上风电中逐渐应用[6-7]．复合筒型基础作为一种宽浅式基础，浅层地基参数取值特别是弹性模量对其动力特性影响较大．有研究表明，地基刚度会对海上风电结构的自振频率产生直接影响[8-9]．因此，地基参数取值对海上风电复合筒型基础设计和校核有着重要影响，成为工程实践中的关键问题．

现有的海上风电基础结构方法常采用等效梁模型法和数值模拟法[8-11]．数值模拟中有限元法在岩土工程中广泛应用，土体本构模型和土体参数的选取往往是关键因素[12]．在土体参数中，国外规范中推荐选取土体的剪切模量等参数[13-14]；我国地勘设计资料中常给出地基压缩模量，这与数值模拟计算中选择土体的弹性模量存在严重矛盾．如何建立土体压缩模量Es与数值模拟中弹性模量E之间的关系，是困扰学者和工程设计者的难题[15]．目前，常用的方法主要有3种：一是根据固结试验和三轴试验，换算值通过查表或地勘报告获得；二是依据工程经验，压缩模量乘以 2～5倍的转换系数可得到弹性模量；三是按照弹性理论建立两者关系，E＝Es[1-2v2/(1-v)]，其中v为泊松比．不同的方法往往得到的结果离散性很大，结果可靠性不高．国内学者对两者转换关系进行研究，如贾堤等[16]通过室内试验获得转换系数为 8.2，可作为天津地区参考值；舒武堂等[17]通过对比试验，统计出武汉地区黏土的转换系数约为 1.46～2.25；杨敏等[18]收集上海地区打桩试验结果，选取 2.5～3.5作为上海软土地区参考值．由此可知，压缩模量与弹性模量间的转换系数具有很强的地域性和经验性[17].然而，对于适用于海上风电结构地基的压缩模量与弹性模量之间的关系研究很少涉及．

鉴于上述原因，基于响水海上风电场地勘资料和海上风电结构原型数据，提出一种基于 MATLAB和ABAQUS的联合仿真方法(简写为 MAT-ABA)，对复合筒型基础复杂层状地基参数进行优化反演研究.开发 MAT-ABA 程序，结合一体化有限元-无限元耦合模型，利用粒子群优化(particle swarm optimization，PSO)算法构建循环参数，优化反演各层地基模量转换系数，再通过风荷载激励下数值模拟获得动态响应与实测数据进行对比验证，说明本文提出的优化反演方法可靠性，也为准确确定海上风电筒型基础地基参数及精确模拟结构动力特性提供一个新的思路与方法．

1 MATLAB与 ABAQUS联合参数优化反演方法

1.1 PSO算法

PSO算法由 Kennedy和 Eberhart在 1995年提出，是一种基于群体智能的在解空间中追寻并搜索最优粒子的算法[19-20]．该算法具有简单易行、收敛速度快、设置参数少、全局智能搜索能力强等优点，在科研和工程实践中得到广泛应用[21-22]．算法基本原理简述如下：假设在1个D维空间中进行搜索，种群中N个粒子具有 3个属性，即当前位置xi、速度vi和粒子个体最优位置pi，而种群具有一个种群历史最优位置pg属性．种群中第i粒子的属性在t次迭代分别表示为

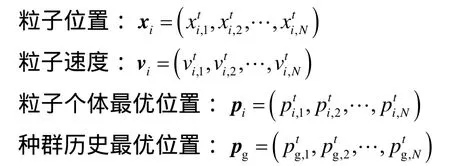
通过评价每个粒子的适应度值，确定当前粒子个体最优位置和种群历史最优位置，然后每个粒子按照下列公式更新自己的位置和速度[22]．

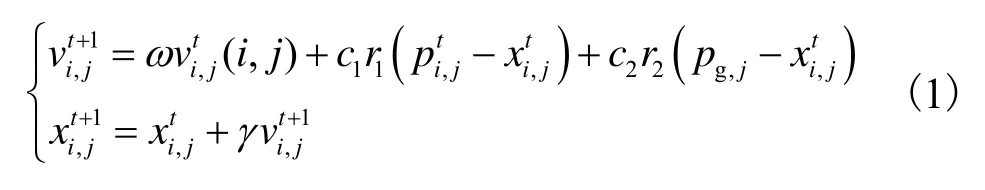
式中：w为惯性权重；c1和c2为学习因子；1r和r2为区间[0，1]上均匀分布的随机数；g为位置更新时约束速度的因子．详细的建议参数取值和计算流程见文献[23]．

1.2 联合参数优化反演程序(MAT-ABA)

提出一种基于ABAQUS和MATLAB联合仿真参数优化反演方法，通过程序调用以达到修改参数、循环模拟、优化识别的目的，并且通过循环理念提高了计算效率，减少人为误差．其示意与伪代码见图1．具体步骤如下．

(1) 编译与调用：以MATLAB编译的PSO算法为主程序，利用system函数调用ABAQUS中inp文件进行仿真计算．

(2) 计算与查找：完成仿真计算后，查找ABAQUS结果文件dat中特定字符，并用textscan函数提取其中目标结果．

(3) 反馈与更新：将目标结果反馈到 MATLAB程序中，参与PSO算法的适应度值计算，以此更新粒子空间位置与速度．

(4) 替换与循环：根据PSO算法循环结果，利用strrep函数替换 inp文件中原来参数，之后再次循环ABAQUS仿真计算，直至满足结束条件．

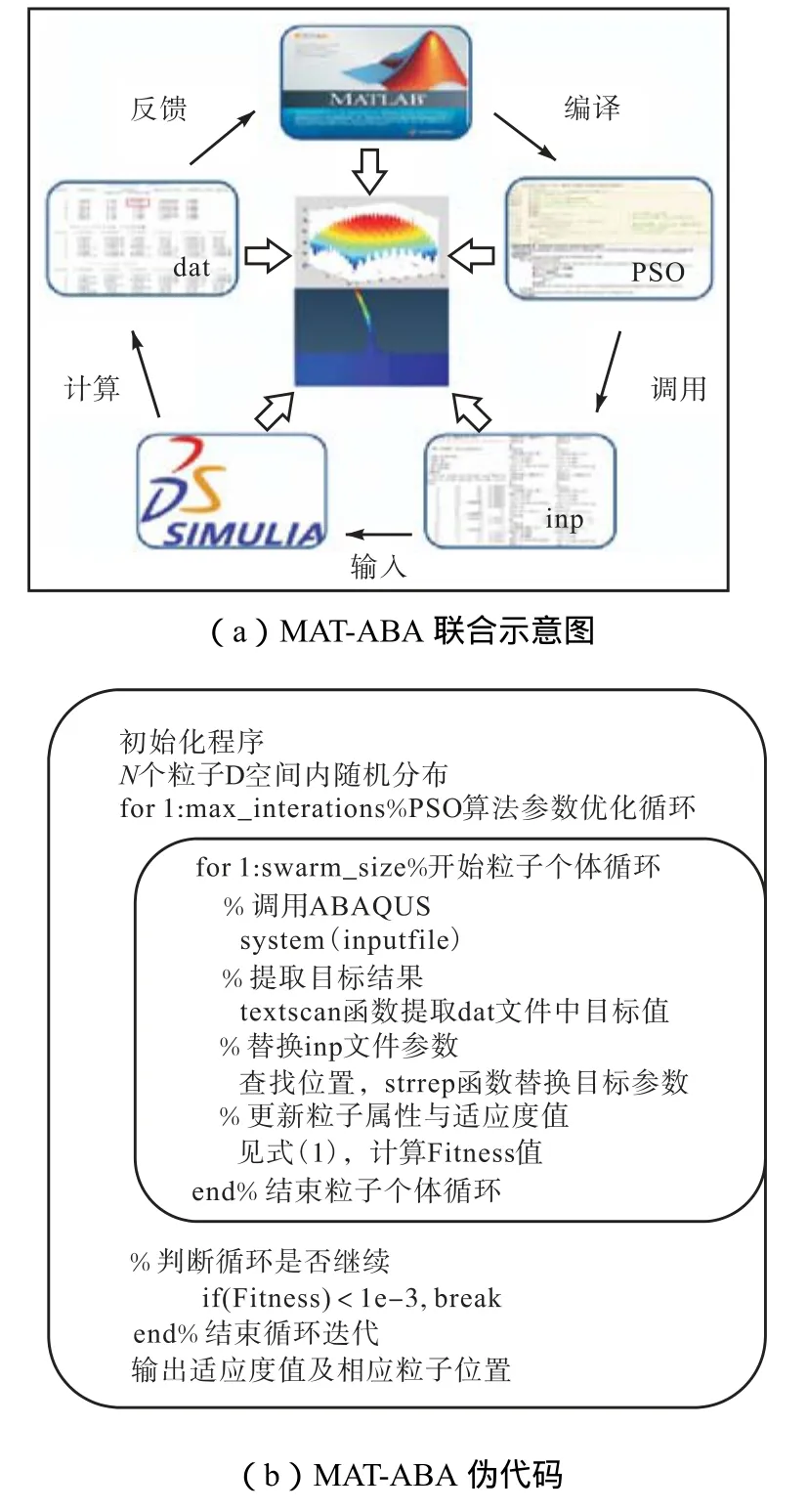
图1 MAT-ABA联合仿真参数优化反演Fig.1 Optimization inversion of parameters by cosimulation of MAT-ABA

2 响水海上风电原型观测

江苏响水近海风电场位于响水县附近海域内，风电场离岸距离约 10km，沿海岸线方向长约 18km，垂直于海岸线方向宽约 2.5～5.5km，风电场海域面积约 91km2．针对响水海上风电筒型基础结构进行原型观测．由图 2可知，响水海上风电包括叶片、塔筒和复合筒型基础，塔筒顶部布置振动位移传感器．该工程结构参数详见表1．

图2 海上风电叶片-塔筒-复合筒型基础结构Fig.2 Offshore wind turbine structures with bladestower-composite bucket foundation

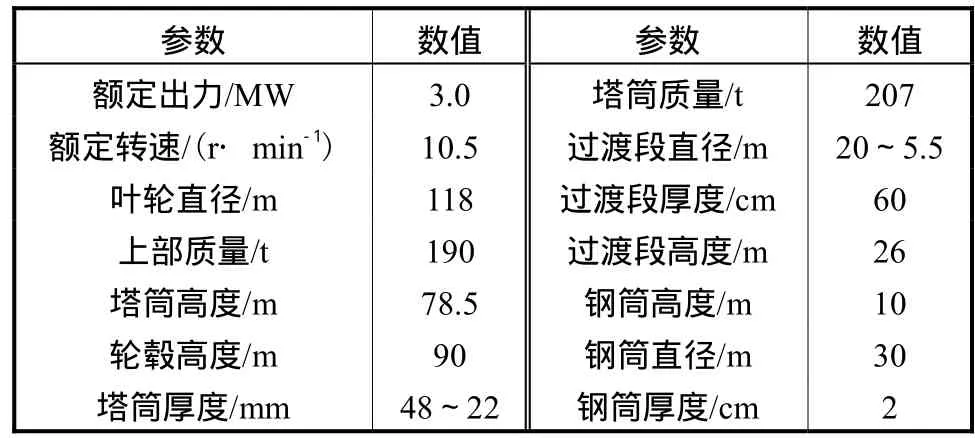
表1 响水海上风电结构参数Tab.1 Offshore wind turbine structure in Xiangshui

图 3给出了现场原型观测获得的停机状态下塔筒顶部振动位移数据频谱，其所对应主频为0.35Hz，该频率是海上风电复合筒型基础结构的 1阶自振频率，采用半功率带宽法计算结构阻尼比[18]，z径向＝2.06%，z切向＝2.12%．

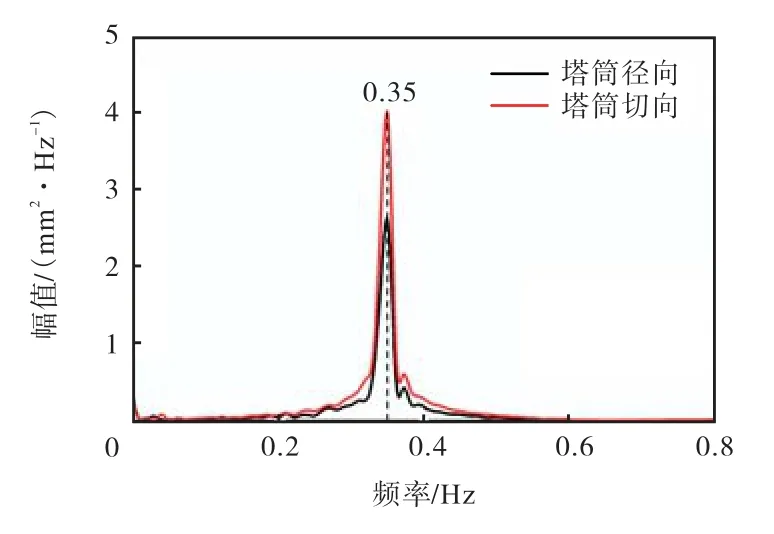
图3 停机工况下的频谱Fig.3 Spectrum for parking case

3 数值模型及风荷载模拟

3.1 数值模型

利用大型有限元分析软件ABAQUS建立详细的三维有限元模型，如图 4所示．塔筒和筒型基础使用3D壳单元模拟，预应力过渡段和土体使用 3D实体单元模拟，预应力钢绞线使用桁架单元模拟．上部结构等效为集中质量块；塔筒高 78.5m，塔筒材料为Q345E钢，建模中塔筒采用弹性模型；复合筒型基础分为下部钢筒、混凝土顶板及预应力混凝土过渡段，底部筒体直径为 30m，筒裙高为 10m，过渡段设置钢绞线，张拉控制应力值为 1320MPa，埋入混凝土过渡段中，混凝土级别为 C60，钢结构为 Q235，结构阻尼采用 Rayleigh阻尼，阻尼比取为 2%[23]．钢材密度为 7850kg/m3，弹性模量为 206GPa，泊松比为0.3．除钢筋与地基外，结构之间相互作用均采用 tie连接．土体与筒型基础使用接触对(contact pair)模拟相互作用，切向摩擦系数为0.3[24]，法向为硬接触．地基土体半径取为4倍筒型基础直径，深度为6倍筒裙高度，土体边界采用无限元边界厚度 10m，避免边界效应影响．土体单元网格数约为 5.6×104，筒型基础含过渡段网格数约为 2.3×104，塔筒与等效质量块网格数约为0.8×104．土层压缩模量、塑性参数见表2，表中 1～6土层分别代表粉土、淤泥质粉质黏土、粉砂、粉质黏土、粉土和粉细砂．

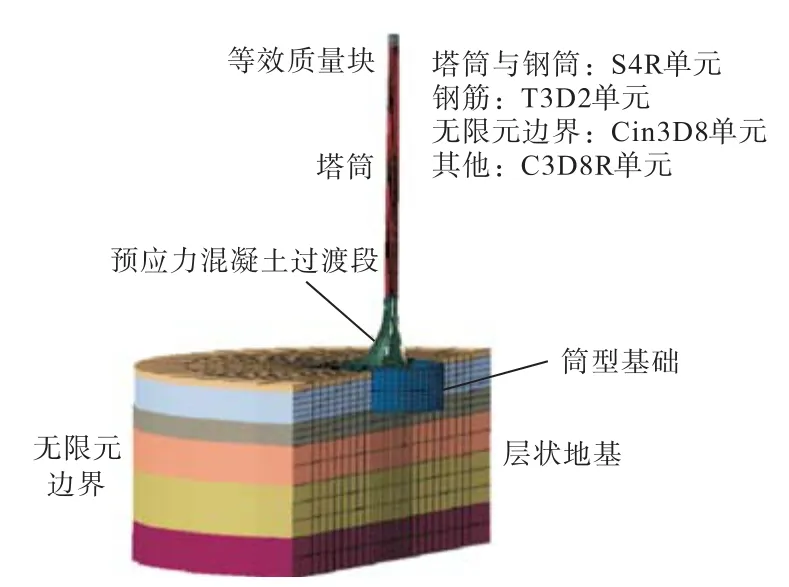
图4 海上风电结构有限元-无限元耦合模型(剖面图)Fig.4 Finite element-infinite element coupling model of offshore wind turbine structure(cross-sectional view)

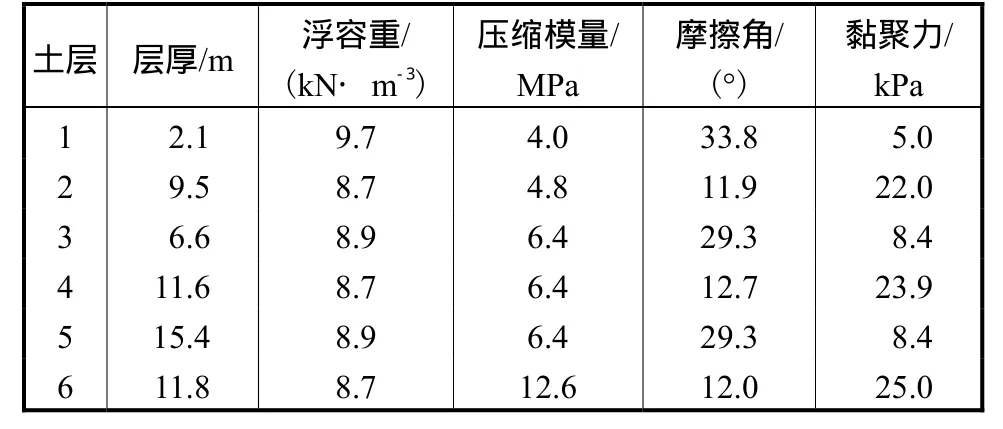
表2 现场土层参数Tab.2 Soil parameters of field

3.2 风荷载模拟

风速是一个随机过程，任意时刻瞬时风速可看作是由平均风速和脉动风速两部分组成，在任意时刻t的瞬时风速U(z,t)可以表示为平均风速和脉动风速u(z,t)之和，即

式中：为风机轮毂处 10min的平均风速；u(z,t)为脉动风速．其中，脉动风速通过脉动风速谱模拟得到．各点平均风速可以通过指数关系计算，即

式中：zb为计算点距海平面高度；z为轮毂处高度；a为极风切变指数，取为0.2[13]．

风速脉动谱反映脉动风速的能量分布，本文选用Kaimal谱[14]作为模拟纵向脉动风速的目标谱．脉动风速模拟方法和塔筒风荷载详见文献[23]和[24]．

海上风机叶片气动荷载应通常采用动量-叶素理论[25]．由于无法得到风机叶片的翼型参数，因此采用无量纲系数对海上风机结构参数进行表征，如功率系数CP和推力系数CT分别表示为

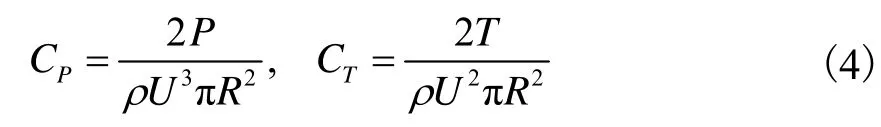
式中：P为风机功率；T为风机受到的推力；R为风机叶片半径；r为空气密度；U为风速．根据公式(4)绘制响水海上风机的功率系数CP与推力系数CT如图5所示．

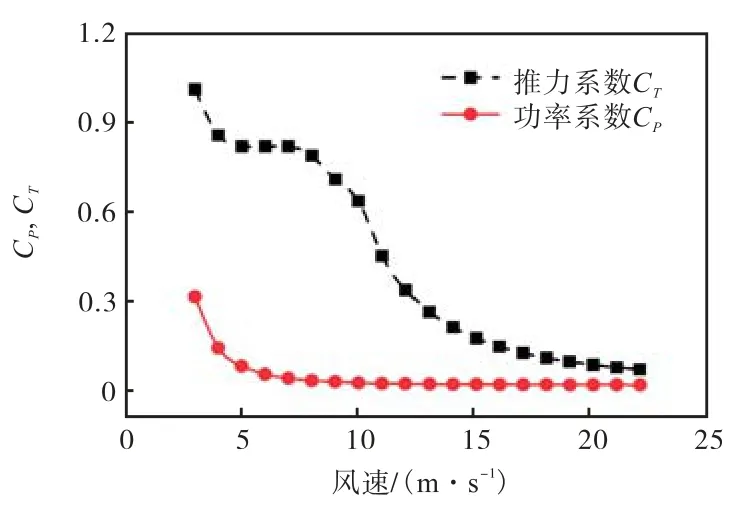
图5 风机功率系数与推力系数Fig.5 Power and thrust coefficients of wind turbine

4 计算结果与分析

4.1 MAT-ABA参数优化反演结果

选用响水海上风电复合筒型基础结构实测分析得到的自振频率为基准(文中自振频率均为1阶自振频率)，将数值模型计算结果与实测结果相对差值定义为适应度值，利用MAT-ABA程序进行复合筒型基础地基参数优化反演研究．

由于筒型基础属于浅层基础，深层土体对该种基础影响较小，经试算和敏感性分析后选取前5层土体进行参数优化反演．基于前人研究成果[19-21]，本文PSO算法设定如下：粒子个数5个，收敛条件适应度值小于 10-3，速度范围[－0.5，1.0]，位置范围[1.0，8.0]．研究表明，经过6至7次迭代后，适应度值满足收敛条件而退出循环优化程序，平均每次迭代用时2150s．图6给出了4次 MAT-ABA程序计算结果，随着迭代次数的增加，数值模型自振频率由初始的0.32Hz左右，逐渐接近目标值 0.35Hz，粒子的位置也发生了相应的变化，向最优值附近聚集，收敛速度较快．同时，最后一次迭代中，不同的粒子位置可能出现均满足收敛要求的情况，选择其中适应度值最优的粒子位置作为参数反演的结果．表 3给出了 4次MAT-ABA程序运行结果，粒子位置代表不同的地基弹性模量与压缩模量的转换系数．虽然最优粒子位置不同，但是平均值在[5.6，6.0]区间内．由此可知，针对本工程而言，由MAT-ABA程序反演得到的转换系数，能够保证数值模型自振频率与实测值一致．

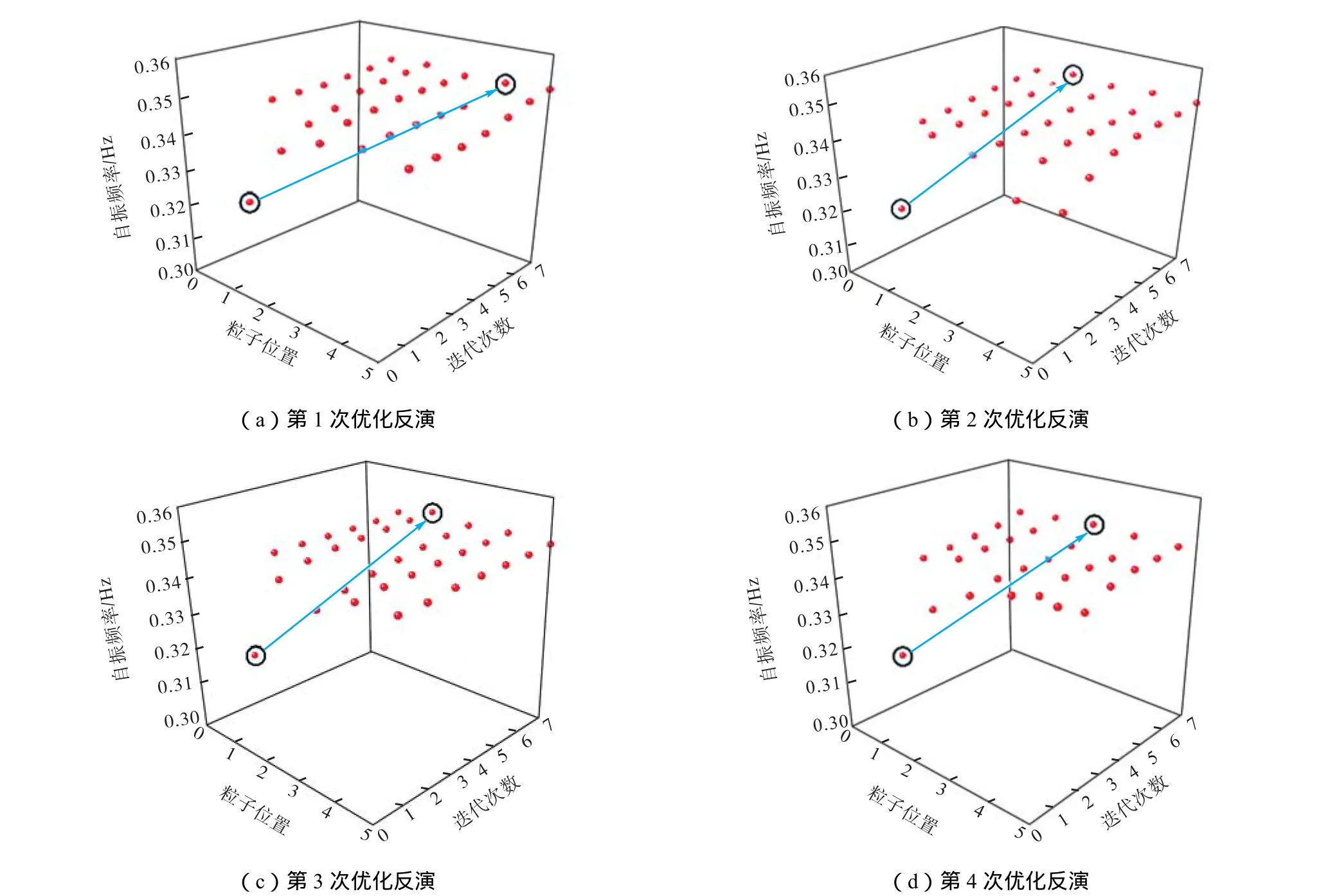
图6 MAT-ABA程序优化反演计算结果Fig.6 Optimization inversion results by MAT-ABA program

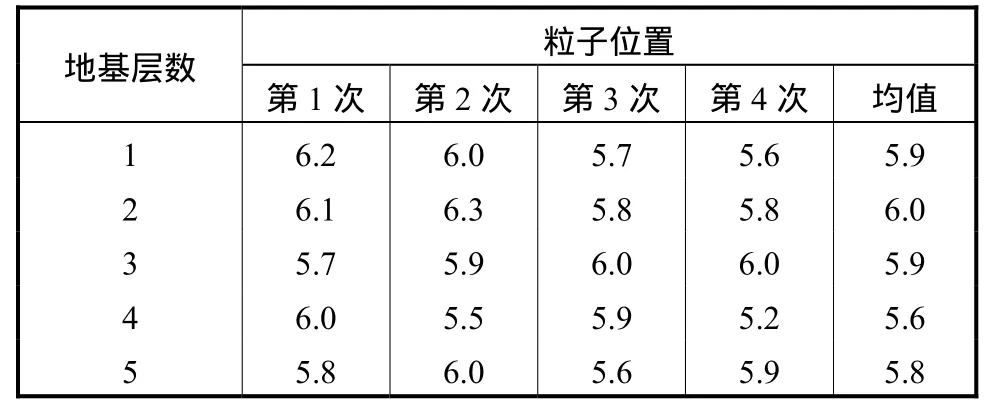
表3 4次MAT-ABA程序最优粒子位置Tab.3 Optimal particle positions in four optimizations by MAT-ABA program

4.2 模拟值与实测值对比

为了进一步验证循环优化反演结果的准确性，本节选取 4种典型的原型观测工况．①停机工况：平均风速 4.6m/s；②低风速运行工况：平均风速 8.5m/s；③中风速运行工况：平均风速 12.8m/s；④高风速运行工况：平均风速 17.1m/s．利用第 3.2节中风荷载模拟方法，得到 4种工况下的风荷载时程，见图7．利用 4次程序得出的转换系数，分别进行海上风电结构数值模拟计算，统计塔筒顶部振动位移的均方根值，并与原型观测获得的实测值进行对比，如图 8所示．由图可知，模拟值与实测值在停机和低风速工况下误差范围较小，而中、高风速误差范围较大，最大误差在 15%以内，模拟结果在合理误差范围内[26].经分析可知，仿真误差随着风速增大而增加，主要原因是风荷载模拟准确性受到影响．图 7中，高风速下风荷载时程波动范围剧烈增加，从而造成模拟与原型观测之间误差增大．

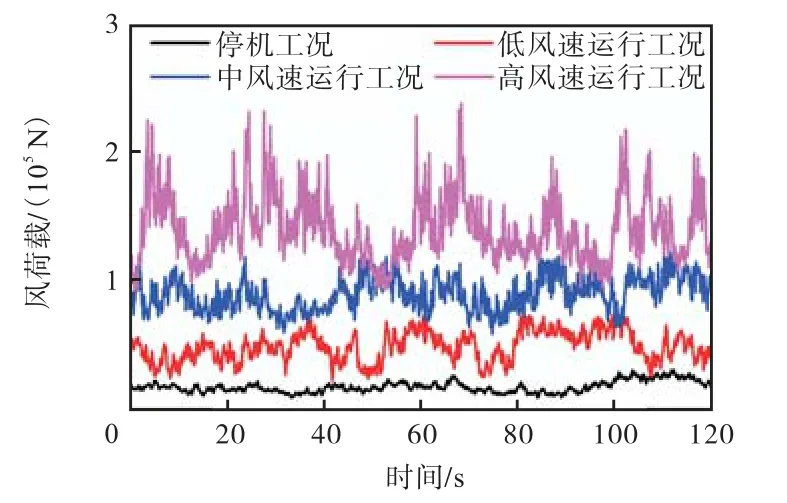
图7 4种工况下风荷载时程曲线(合力)Fig.7 Time history curves of wind load for four cases(total loads)

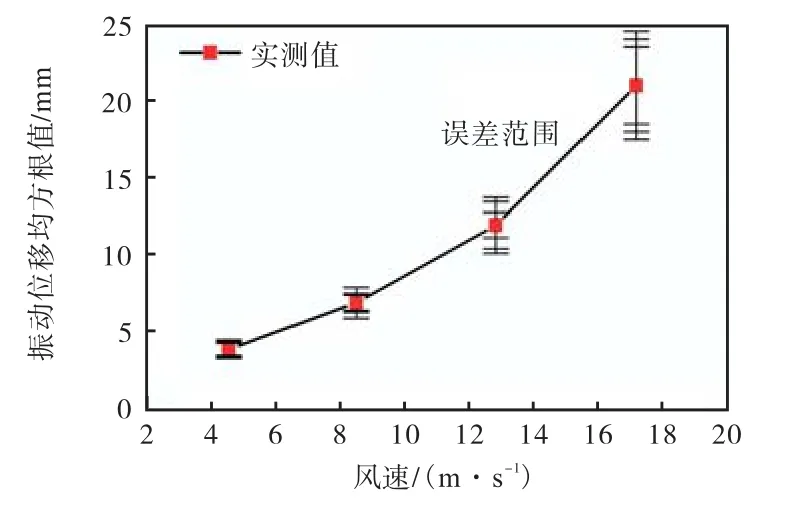
图8 塔筒顶部振动位移模拟值误差分析Fig.8 Error analysis of simulated vibration displacement at tower top

5 结 论

为确定海上风电筒型基础地基弹性模量与压缩模量的转换关系，提出一种基于 MATLAB和ABAQUS的联合仿真方法，对筒型基础复杂层状地基参数优化反演分析，并通过原型观测值动力特性对识别参数准确性进行验证．通过本文工作，主要结论总结如下．

(1) 开发基于PSO算法的MATLAB程序，循环调用 ABAQUS进行计算程序(MAT-ABA)，实现了智能算法与高效数值仿真的结合，为参数循环优化反演提供了一个新的思路．

(2) 基于响水海上风电复合筒型基础结构原型观测数据与地勘资料，通过MAT-ABA优化反演到的参数，可以看出复杂层状地基弹性模量与压缩模量转换系数在[5.6，6.0]区间内．同时，基于优化反演参数模拟，获得在风荷载作用下风机振动响应，与实测结构响应间误差均小于 15%，在合理范围之内，验证了该程序与方法的准确性与可靠性．此外，通过改进风荷载模拟方法能够降低仿真误差，同时考虑海洋地基土体塑性的多参数优化反演是进一步研究的方向．

(3) 虽然仅以响水海上风电复合筒型基础结构为研究对象开展研究，但是对其他类型的风电基础结构基于振动的参数优化反演也具有一定的参考价值与借鉴意义．

[1] Sahu B K.Wind energy developments and policies in China：A short review[J].Renewable and Sustainable Energy Reviews，2017，81(1)：1393-1405.

[2] Oh K Y，Nam W，Ryu M S，et al.A review of foundations of offshore wind energy convertors: Current status and future perspectives[J].Renewable and Sustainable Energy Reviews，2018，88：16-36.

[3] Carswell W，Johansson J，Løvholt F，et al.Foundation damping and the dynamics of offshore wind turbine monopoles[J].Renewable Energy，2015，80：724-736.

[4] Willis D J，Niezrecki C，Kuchma D，et al.Wind energy research：State-of-the-art and future research directions[J].Renewable Energy，2018，125：133-154.

[5] Wang X，Zeng X，Li J，et al.A review on recent advancements of substructures for offshore wind turbines[J].Energy Conversion and Management，2018，158：103-119.

[6] Lian Jijian，Sun Liqiang，Zhang Jinfeng，et al.Bearing capacity and technical advantages of composite bucket foundation of offshore wind turbines[J].Transactions of Tianjin University，2011，17(2)：132-137.

[7] Lian Jijian，Ding Hongyan，Zhang Puyang，et al.Design of large-scale prestressing bucket foundation for offshore wind turbines[J].Transactions of Tianjin University，2012，18(2)：79-84.

[8] Arany L，Bhattacharya S，Macdonald J H G，et al.Closed form solution of Eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI[J].Soil Dynamics and Earthquake Engineering，2016，83：18-32.

[9] Arany L，Bhattacharya S，Adhikari S，et al.An analytical model to predict the natural frequency of offshore wind turbines on three-spring flexible foundations using two different beam models[J].Soil Dynamics and Earthquake Engineering，2015，74：40-45.

[10] Lombardi D，Bhattacharya S，Wood D M.Dynamic soil-structure interaction of monopile supported wind turbines in cohesive soil[J].Soil Dynamics and Earthquake Engineering，2013，49：165-180.

[11] Bisoi S，Haldar S.Design of monopile supported offshore wind turbine in clay considering dynamic soilstructure-interaction[J].Soil Dynamics and Earthquake Engineering，2015，73：103-117.

[12] 高大钊．土力学与基础工程[M].北京：中国建筑工业出版社，2004.

Gao Dazhao.Soil Mechanics and Foundation Engineering[M].Beijing：China Architecture & Building Press，2004(in Chinese).

[13] Veritas D N.Design of Offshore Wind Turbine Structures[S].Offshore Standard DNV-OS-J101，2004.

[14] International Electrotechnical Commission.IEC 61400-1：Wind Turbines Part 1：Design Requirements[S].International Electrotechnical Commission，2005.

[15] 陈勇华.土体压缩模量，变形模量和弹性模量的讨论[J].城市建设，2010，66：135-136.

Chen Yonghua.Discussion on soil compression modulus，deformation modulus and elastic modulus[J].Chengshi Jianshe，2010，66(1)：135-136(in Chinese).

[16] 贾 堤，石 峰，郑 刚，等.深基坑工程数值模拟土体弹性模量取值的探讨[J].岩土工程学报，2008，30(1)：155-158.

Jia Di，Shi Feng，Zheng Gang，et al.Elastic modulus of soil used in numerical simulation of deep foundation pits[J].Chinese Journal of Geotechnical Engineering，2008，30(1)：155-158(in Chinese).

[17] 舒武堂，李国胜，蒋 涛.武汉地区淤泥质软土、粘性土的压缩模量与变形模量的相关关系[J].岩土工程界，2004，7(7)：29-30.

Shu Wutang，Li Guosheng，Jiang Tao.Relationship between compressive modulus and deformation modulus of clay soil in Wuhan region[J].Geotechnical Engineering World，2004，7(7)：29-30(in Chinese).

[18] 杨 敏，赵锡宏.分层土中的单桩分析法[J].同济大学学报：自然科学版，1992，20(4)：421-428.

Yang Min，Zhao Xihong.An approach for a single pile in layer soil[J].Journal of Tongji University：Natural Science，1992，20(4)：421-428(in Chinese).

[19] 郭文忠，陈国龙.离散粒子群优化算法及其应用[M].北京：清华大学出版社，2012.

Guo Wenzhong，Chen Guolong.Discrete Particle Swarm Optimization(PSO) and Its Application[M].Beijing：Tsinghua University Press，2012(in Chinese).

[20] Cheng S，Lu H，Lei X，etal.A quarter century of particle swarm optimization[J].Complex & Intelligent Systems，2018，4(3)：1-13.

[21] 刘欣蔚，王 浩，雷晓辉，等.粒子群算法参数设置对新安江模型模拟结果的影响研究[J].南水北调与水利科技，2018，16(1)：69-74.

Liu Xinwei，Wang Hao，LeiXiaohui，et al.Influence of parameter setting in PSOalgorithm on simulation results of Xin’anjiang model[J].South-to-North Water Transfers and Water Science& Technology，2018，16(1)：69-74(in Chinese).

[22] El-Shorbagy M A，Hassanien A E.Particle swarm optimization from theory to applications[J].International Journal of Rough Sets andData Analysis，2018，5(2)：1-24.

[23] 董霄峰.海上风机结构振动特性分析与动态参数识别研究[D].天津：天津大学建筑工程学院，2014.

Dong Xiaofeng.Vibration Behavior Analysis and Dynamic Parameter Identification of Offshore Wind Turbine Structure[D].Tianjin：School of Civil Engineering，Tianjin University，2014(in Chinese).

[24] 于通顺，王海军.循环荷载下复合筒型基础地基孔隙水压力变化及液化分析[J].岩土力学，2014，35(3)：820-826.

Yu Tongshun，Wang Haijun.Pore water pressure fluctuation and liquefaction analysis of subgrade for composite bucket foundation under cyclic loading[J].Rock and Soil Mechanics，2014，35(3)：820-826(in Chinese).

[25] 盛振国，任慧龙，甄春博，等.基于时域载荷的海上风机基础结构疲劳分析[J].华中科技大学学报：自然科学版，2014，42(4)：96-100.

Sheng Zhenguo，Ren Huilong，Zhen Chunbo，et al.Fatigue analysis for offshore wind turbine foundation structures based on loads in time domain[J].Journal of Huazhong University of Science and Technology：Natural Science Edition，2014，42(4)：96-100(in Chinese).

[26] 梁 力，李 明.土木工程结构数值计算与仿真分析方法[M].沈阳：东北大学出版社，2014.

Liang Li，Li Ming.Numerical Calculation and Simulation Methods in Civil Engineering Structure[M].Shenyang：Northeast University Press，2014(in Chinese).