大跨度悬索桥冲击系数影响因素研究

朱劲松 ，香 超，祁海东

(1.天津大学建筑工程学院，天津 300072；2.滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072；3.怀来县市政建设管理处，怀来 075400)

悬索桥因其具有跨越能力强、结构受力合理、自重轻和造型优美等特点，目前已广泛应用于公路桥梁建设中．我国《公路桥涵设计通用规范》(JTG D60—2015)[1](以下简称为15规范)中规定利用结构基频计算车辆冲击系数，其主要针对中小跨径桥梁的结构整体进行计算．对于大跨度悬索桥，由于结构动力特性显著变化，结构振动频率较低，各构件刚度有明显区别，现行规范中冲击系数计算公式的适用性仍有待研究．冲击系数受多种因素影响，而且这些影响因素的作用程度是不同的，因此，有必要基于车桥耦合振动理论，研究大跨度悬索桥冲击系数受各因素的影响规律，并对影响因素进行敏感性分析，研究成果将对悬索桥结构设计及后期养护具有重要指导意义.

国内外许多学者对公路桥梁冲击系数及其影响规律进行了大量的研究，但对于大跨度悬索桥及其冲击系数影响因素的研究较少．王达等[2]基于分离法对某悬索桥在 3种不同桥面粗糙度下的动力响应进行了研究，结果发现悬索桥结构各部分对应的冲击系数有明显的差异．王小松等[3]通过研究不同车速、桥面不平度情况下的悬索桥各构件的冲击系数，得出现行规范中冲击系数取值对悬索桥部分内力效应偏于不安全．周勇军等[4]通过正交实验，对某刚构-连续组合梁桥的冲击系数进行影响因素灵敏度分析，为将冲击系数定义为多因素函数表达式指明方向．王贵春等[5]利用 ANSYS软件分析了在不同车速、车重、桥面不平顺度情况下斜拉桥不同构件的动力响应．朱劲松等[6]基于车桥耦合振动动力响应分析研究了中下承式拱桥在汽车荷载作用下的吊杆所受冲击作用不均匀性问题．上述关于车辆对桥梁冲击作用的研究主要集中于单一因素影响的定性分析，多影响因素分析则主要针对中小跨径的简单桥型，而对大跨度悬索桥结构冲击系数及其影响因素的敏感性分析较少，同时车桥耦合振动对悬索桥刚度明显不同的局部构件的影响程度也有待进一步的研究．

本文研究以某大跨度悬索桥为背景，建立相应的整体有限元计算模型，通过车桥耦合振动分析方法，系统地研究了车速、车重、横向加载位置、桥面不平顺对悬索桥加劲梁挠度及弯矩、主塔塔顶水平位移及吊杆轴力冲击系数的影响规律，并针对各影响因素进行敏感性分析，所得研究成果为大跨度悬索桥冲击作用研究及后续规范修订中对该类悬索桥的研究提供参考依据．

1 车桥耦合振动数值分析方法

1.1 三维空间汽车模型

为了更好地模拟公路桥梁在汽车荷载作用下的动力响应，选用三轴拖车型卡车[7]进行车桥耦合振动分析．三轴车辆的理想化模型简化为车体、悬挂装置、车轴等组成，该模型共 11个独立自由度，其中yw1～yw6为 6个车轮的竖向自由度，yc1、yc2为车头与车厢的竖向自由度，qc1是车头的点头自由度，jc1、jc2是车头与车厢的侧向滚动自由度．采用弹簧-阻尼系统模拟车辆的悬挂系统及路面与车轮的相互作用，其中mc1、mc2为车头和车厢的质量，mw1～mw6是6个车轮的质量，ks1～ks6、cs1～cs6是悬挂系统刚度与阻尼，kt1～kt6、ct1～ct2是轮胎刚度与阻尼．三维空间汽车模型见图1．

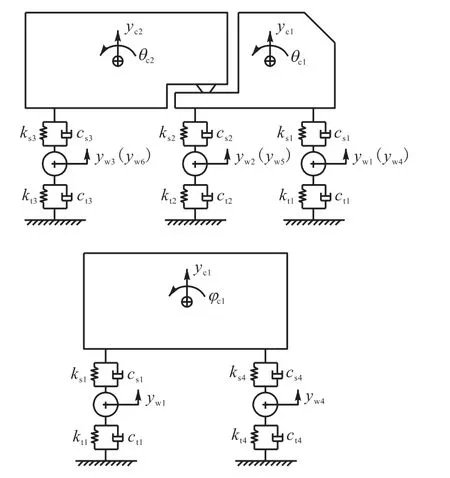
图1 三维空间汽车模型Fig.1 Three-dimensional vehicle model

1.2 桥面不平顺度模拟

桥面不平顺度是影响车桥系统耦合振动的主要因素之一．桥面不平顺度是一个随机空间过程，本身具有不确定性，可通过多种方法表达．本文将桥面不平顺度定义为零均值且服从稳态高斯分布的随机过程，基于功率谱密度函数，利用三角级数叠加法得出桥面不平顺度函数[8]

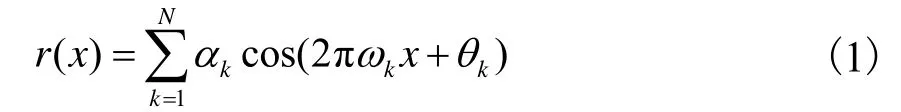
式中：a为余弦函数的幅值，

k，S(w)k为路面功率谱函数；wk=wu+(k- 12)Dw，wk为位于区间[wu,wt] 内的频率，；x为桥面上某点到上桥端的水平距离；qk表示在[0,2π]满足均匀分布的相位差；N表示随机平顺度模拟所需的点数．根据路面功率谱密度函数(a表示桥面粗糙度系数[9])，将桥面平顺度分为5个等级，表1为各等级桥面分级标准．表中规定了本文分析中各级桥面粗糙度系数a的取值及各级桥面不平顺极值．以3级路面为例，图2为通过计算模拟程序生成的桥面不平顺度样本．

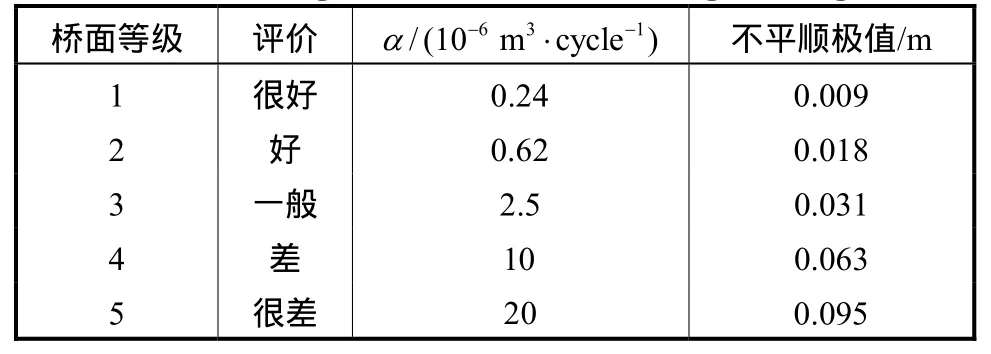
表1 各等级桥面分级标准Tab.1 Grading standard for each bridge deck grade

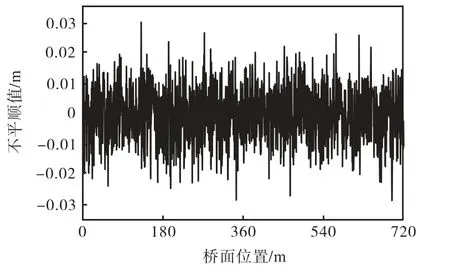
图2 3级路面不平顺样本曲线Fig.2 Sample curve of road surface roughness for grade 3

1.3 车桥耦合振动方程

车桥耦合振动系统中假定车轮与桥面始终接触，桥梁与车辆在车轮与桥面接触处具有相同的位移协调条件，对于车辆而言桥梁的变形相当于附加桥面不平顺度．分析中将桥梁变形引起的附加桥面不平顺度和随机桥面不平顺度进行组合成等效不平顺度，将等效不平顺作为系统激振源．车轮与桥梁接触点处，车辆所受荷载和桥梁所受荷载是一组大小相等、方向相反的相互作用力[10]．

利用有限元法，建立的桥梁结构的振动微分方程为

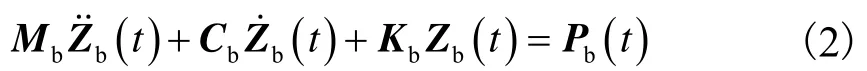
式中：分别为桥梁系统的加速度向量、速度向量、位移向量和等效节点力向量；Mb、Cb、Kb分别为桥梁系统的质量矩阵、阻尼矩阵、刚度矩阵．

根据建立的三轴车辆模型，利用动力平衡原理，建立车辆振动微分方程

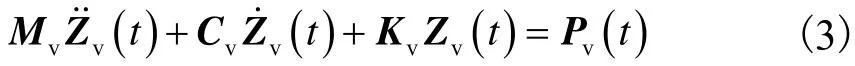
式中：)分别为车辆系统的加速度向量、速度向量、位移向量和等效节点力向量；Mv、Cv、Kv分别为车辆系统的质量矩阵、阻尼矩阵、刚度矩阵．

在求解车桥耦合振动微分方程时，依据上述车辆与桥梁系统之间的位移和力的协调条件，建立车桥耦合振动微分方程

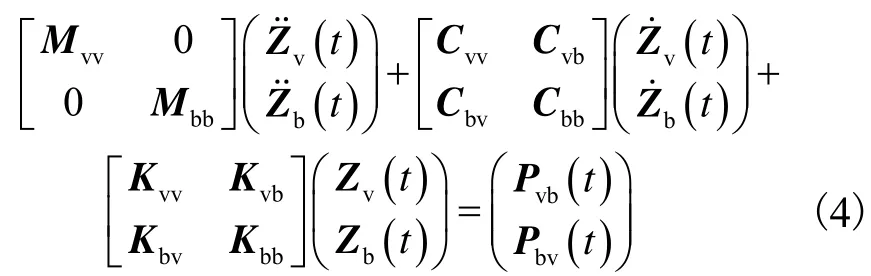
车桥耦合振动方程中质量矩阵、阻尼矩阵、刚度矩阵可由车桥耦合条件推导而出，限于篇幅不再详细列出，详见文献[6]．

2 桥梁算例

2.1 桥梁概况

官厅水库特大桥位于河北省境内，主桥为主跨720m 的钢-混组合梁单跨悬索桥，道路等级为城市主干路，设计速度为 60km/h，双向六车道；主塔采用门式框架结构，主塔基础采用分离式承台，两岸锚碇均为重力式锚碇，沉井基础；主缆跨度(210＋720＋210)m，主缆矢跨比 1/9.5，主缆采用预制平行钢丝索股，每根主缆由91股127～5.25mm高强钢丝组成；加劲梁采用钢-混组合梁，总宽33.6m，梁高3.023m，由主纵梁、次纵梁、钢横梁和混凝土桥面板组成．主桥总体布置见图3．

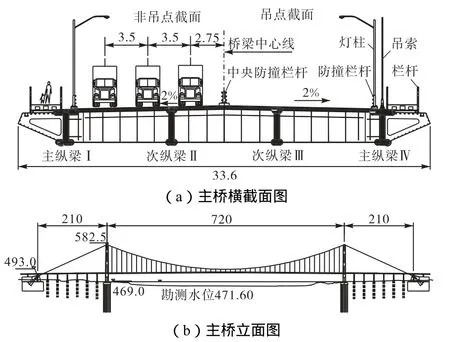
图3 主桥总体布置(单位：m)Fig.3 General arrangement of the main bridge(unit：m)

2.2 有限元模型

本文采用通用有限元软件 ANSYS建立官厅水库特大桥悬索桥的有限元模型，对主塔、主缆和加劲梁进行精细模拟．该桥的加劲梁采用梁格法建模，4根纵梁(Ⅰ～Ⅳ)分别用相互独立的梁单元模拟，纵梁之间通过横梁相连，主塔各构件采用梁单元模拟，主缆和吊索采用杆单元模拟，吊杆与加劲梁及吊杆与主缆之间采用共节点相连．整个模型共12755个单元，6022个节点．

2.3 结构自振特性分析

结构自振特性分析是进行动力响应分析研究的重要依据[11]，利用ANSYS对上述悬索桥进行模态分析，前 10阶振型的频率和振型描述如表 2所示，并在图4中给出了前4阶振型．该桥基频为0.142Hz，根据现行15规范，汽车冲击系数应取为0.05．

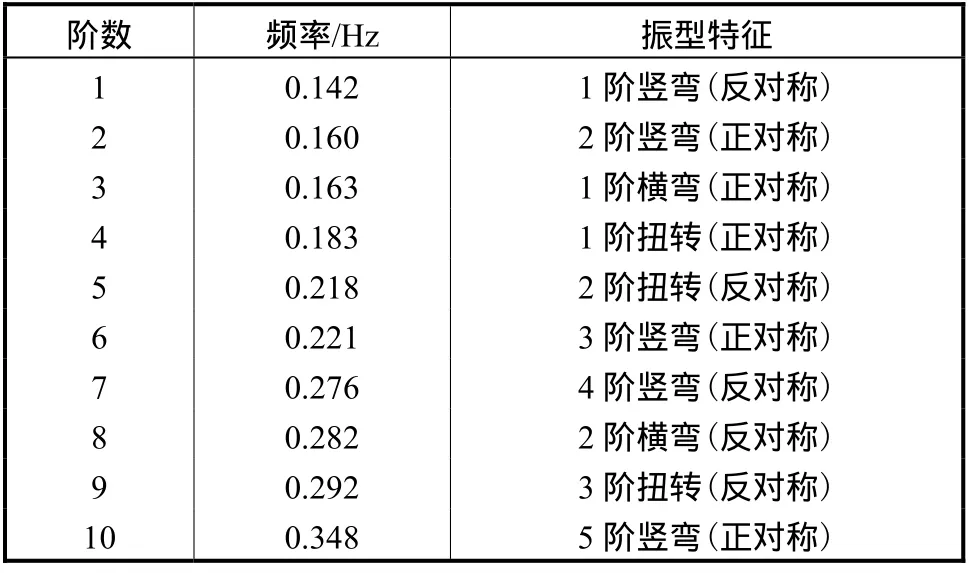
表2 桥梁的主要自振频率以及振型Tab.2 Frequencies and modal shapes of main modes of the bridge

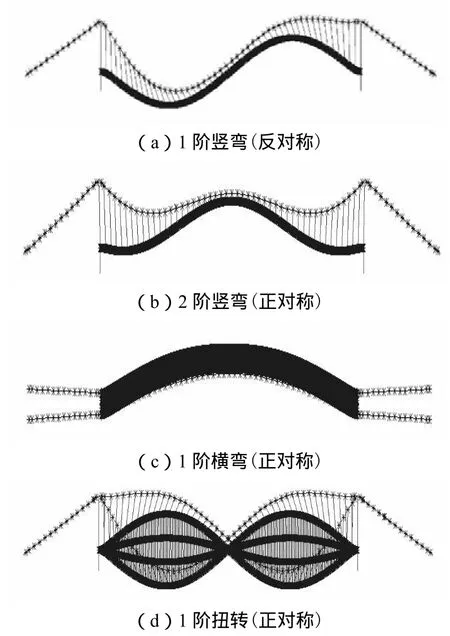
图4 前4阶桥梁自振振型Fig.4 First 4 mode shapes of the bridge

2.4 计算工况

实际上，汽车对桥梁的冲击系数的影响因素多而复杂，包含桥梁结构特性、车辆动力特性、桥面不平顺度、车速、车重、横向加载位置等．因此依据上述计算模型和原理，利用 MATLAB软件编写车桥耦合振动数值模拟程序，对该桥进行车桥耦合振动数值分析，分别计算桥面不平顺度、车速、车重及车辆横向加载位置等因素对桥梁动力响应及其冲击系数的影响．计算工况如表 3所示，当对某一影响因素进行工况分析时，该影响因素依次取变化范围内的参数值，其余因素均取典型值．同时，汽车行驶过程中，主纵梁及次纵梁所受动力冲击作用不同[12]．因此，在计算横向加载位置对冲击系数的影响时，取4纵梁跨中截面的挠度冲击系数进行分析比较，在其他工况计算时，取主纵梁Ⅰ的 1/8、1/4、3/8、1/2跨挠度及弯矩冲击系数．另外，为了分析桥塔及不同位置处的吊杆所受冲击作用的大小，取塔顶水平位移、1/4跨吊杆索力、1/2跨吊杆索力进行计算分析．

表3 计算工况Tab.3 Calculation conditions

3 结果分析

3.1 车速对冲击系数的影响

车辆以不同的速度经过桥梁时，结构所受的激励不同，其各构件的动力响应必然不同[13]．为研究汽车速度的影响，分别计算车辆速度不同时桥梁各构件的动力响应及其冲击系数．

以主纵梁Ⅰ为研究对象，主纵梁挠度冲击系数m随车速变化的曲线如图 5(a)所示．由图可见，主纵梁各截面冲击系数均明显高于规范值0.05，并且其不随速度的加快而持续增加，对主纵梁1/8跨及1/2跨截面而言，车速从 20km/h增加到 60km/h时，其挠度冲击系数变化到最大，当车速继续增加到 100km/h时，冲击系数逐步减小．对于主纵梁 1/4及 3/8跨截面，在车速低于 60km/h时，其挠度冲击系数随车速增加而增大，当车速达到 80km/h时，冲击系数迅速减小，当车速再继续增加到100km/h时，冲击系数又急剧增大．同时，车速相同时主纵梁各截面的挠度冲击系数有明显的差异，各截面冲击系数达到极值时的车速也不尽相同．在车辆低速时主纵梁1/8跨截面的挠度冲击系数较大，在车辆高速时主纵梁 1/4跨及3/8跨截面的冲击系数较大，当车速在 60km/h左右时，跨中截面冲击系数较大．主纵梁弯矩冲击系数随车速变化的曲线如图5(b)所示．结果表明，各截面弯矩冲击系数比挠度冲击系数较小，其变化趋势与速度没有明显联系，在车速较低时，主纵梁各截面中 1/8跨及1/2跨截面的弯矩冲击系数较大．

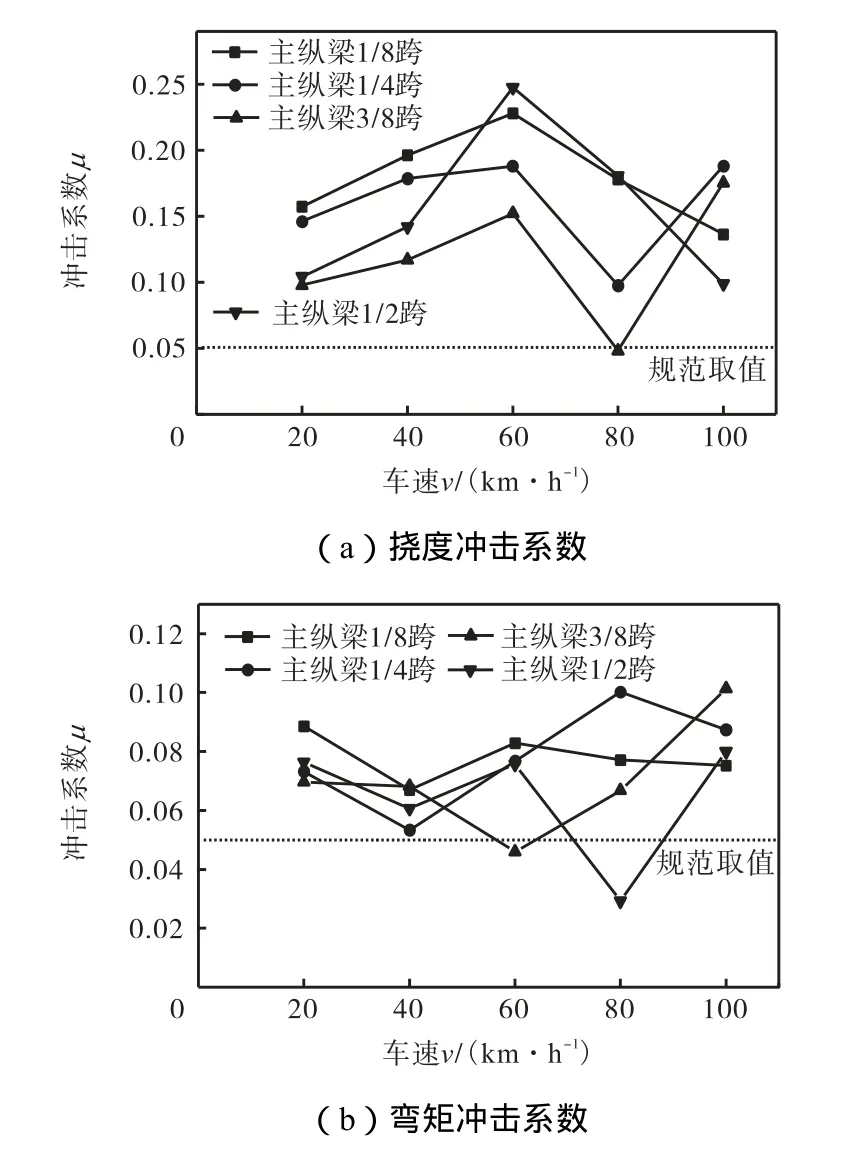
图5 主纵梁Ⅰ冲击系数随车速的变化Fig.5 Variation of impact coefficient with vehicle velocity at main beamⅠ

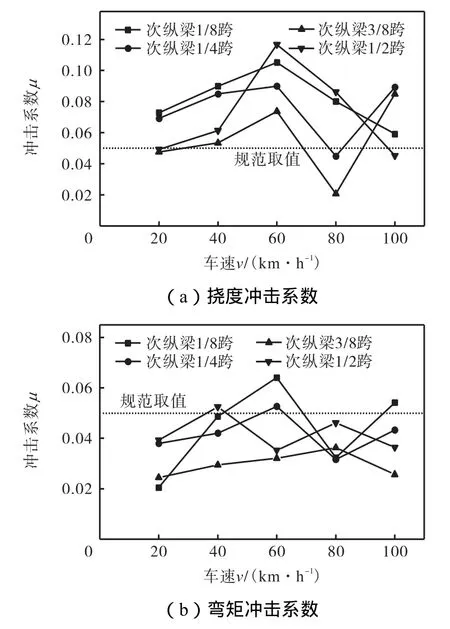
图6 次纵梁Ⅱ冲击系数随车速的变化Fig.6 Variation of impact coefficient with vehicle velocity at secondary beamⅡ

以次纵梁Ⅱ为例，次纵梁挠度冲击系数随车速变化的曲线如图 6(a)所示．由图可见，次纵梁各截面挠度冲击系数与主纵梁各截面挠度冲击系数随速度增加的变化趋势基本吻合，除个别点外，次纵梁挠度冲击系数约为主纵梁挠度冲击系数的 1/2．次纵梁弯矩冲击系数随车速变化的曲线如图 6(b)所示．结果表明，绝大部分次纵梁截面弯矩冲击系数低于规范值0.05，与主纵梁弯矩冲击系数比较，没有明显联系；同时各截面弯矩冲击系数随速度变化趋势均不相同，其取得极值所对应的行车速度亦有差别．

桥塔塔顶水平位移冲击系数随车速变化的曲线如图 7所示．由图可见，随着行车速度的增加，其位移冲击系数先增加再减小，在车速为80km/h时达到最大．同时，在低速行驶时，车辆驶离侧桥塔塔顶水平位移冲击系数较大，在高速行驶时，车辆驶向侧桥塔塔顶水平位移冲击系数较大．

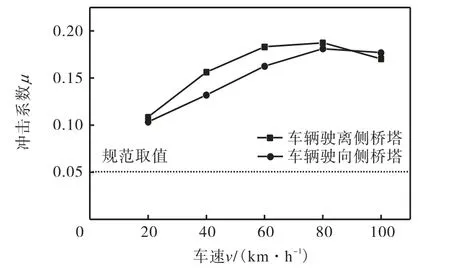
图7 塔顶水平位移冲击系数随车速的变化Fig.7 Variation of impact coefficient of horizontal displacement on the top of main tower with vehicle velocity

吊杆轴力冲击系数随车速变化的曲线如图 8所示．由图可见，在车辆低速行驶时，吊杆轴力冲击系数均小于规范值 0.05；随着车速增加，其中 1/8跨及1/4跨吊杆在速度为80km/h时达到最大，3/8跨吊杆在速度为60km/h与100km/h时较大，1/2跨吊杆在速度为60km/h时达到最大．将桥跨各位置上主纵梁弯矩与吊杆轴力的冲击系数对比分析，两者随速度增加的变化趋势接近，且吊杆轴力冲击系数较小．

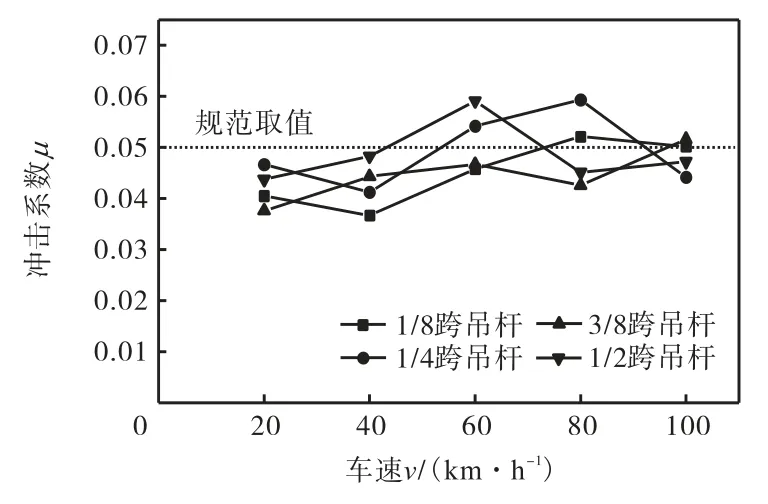
图8 吊杆轴力冲击系数随车速的变化Fig.8 Variation of impact coefficient of shaft force with vehicle velocity

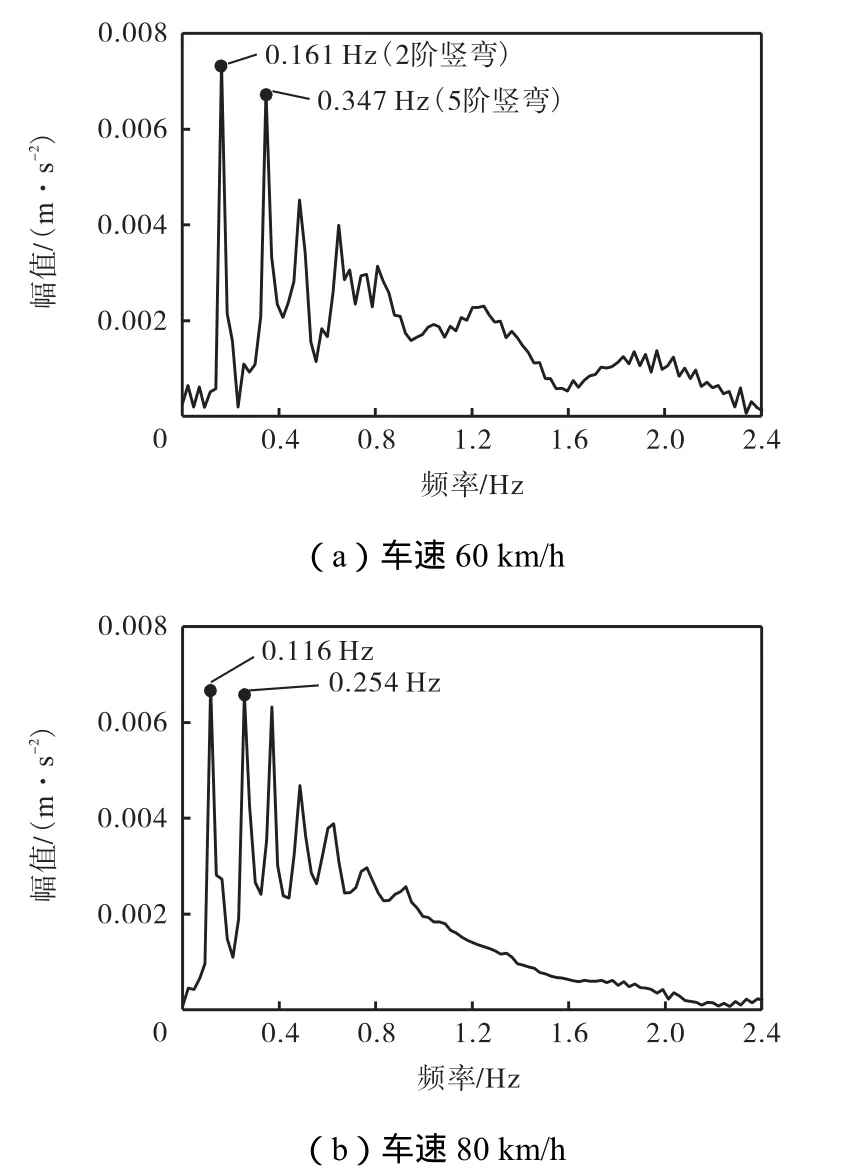
图9 主纵梁跨中截面的加速度响应频谱曲线Fig.9 Frequency spectrum of acceleration responses in the midspan of main beam

据上述主纵梁挠度冲击系数分布情况可知，在车速达到 80 km/h时，各个位置的冲击系数均明显减小，说明车速持续增加不一定增大车辆对桥梁的动力效应[11]．为消除静位移的影响，选取加速度响应进行频谱分析来解释这一现象．图 9为主纵梁跨中截面在车速为60km/h与80km/h的加速度响应的频谱曲线．由图可见，当车速为 60km/h时，加速度响应谱中的卓越振动频率与桥梁自振频率中的竖弯频率值接近，当车速为 80km/h时，桥梁自振频率与加速度响应谱中的卓越振动频率相差较大，因此各截面的位移冲击系数均明显下降．这主要是因为随着车速的变化，汽车对桥梁的激振力频率改变，导致卓越振动频率不同．主纵梁跨中截面在不同速度下的挠度时程曲线如图 10(a)所示，主塔塔顶水平位移时程曲线如图10(b)所示．

3.2 桥面不平顺度对冲击系数的影响

在不同桥面平顺度下行驶的汽车对桥梁的动力冲击效应也会不同，且区别显著[14]．为研究桥面不平顺度对结构各构件的冲击作用的影响，分别计算桥面不平顺度变化时桥梁结构各构件的冲击系数．

图10 位移时程曲线Fig.10 Time-history curve of displacement

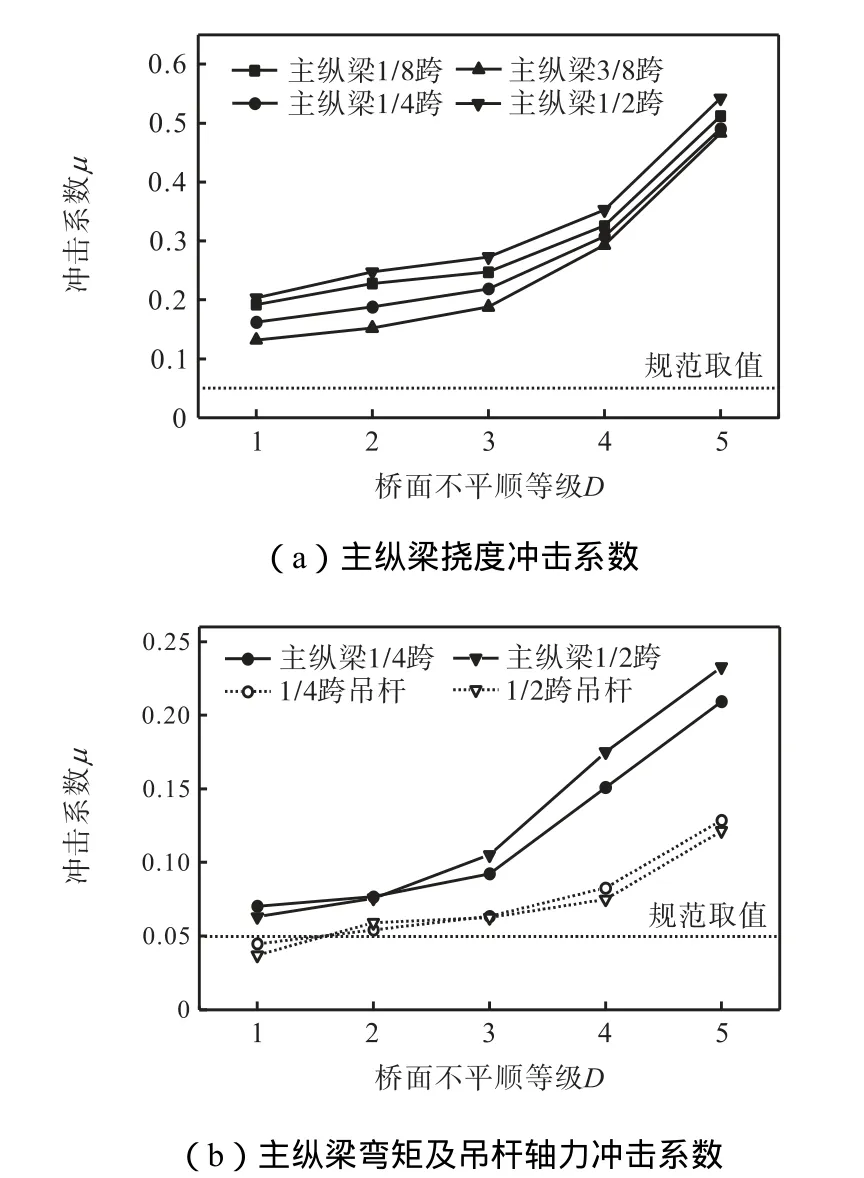
图11 冲击系数随桥面不平顺等级的变化Fig.11 Variation of impact coefficient with road surface roughness grade

主纵梁挠度冲击系数随桥面不平顺等级变化的曲线如图 11(a)所示．分析可知，随着桥面粗糙度增加，主纵梁各截面冲击系数随之增大，且增幅变大．例如当桥面不平顺为 2级时，主纵梁跨中截面的冲击系数达到 0.248，之后其逐级差值分别为 0.03，0.09，0.18．另外相同桥面不平顺等级时，主纵梁各截面冲击系数为 1/2跨＞1/8跨＞1/4跨＞3/8跨，同时各截面冲击系数差值随桥面不平顺增大而减小．

主纵梁弯矩及吊杆轴力冲击系数随桥面不平顺等级变化的曲线如图 11(b)所示．分析结果表明，桥面平顺度较好时，主纵梁 1/4跨弯矩冲击系数较大，随着桥面平顺度变差，主纵梁1/2跨弯矩冲击系数较大．桥面粗糙度增加，跨中短吊杆冲击系数高于 1/4跨长吊杆．将桥跨各位置上主纵梁弯矩与吊杆轴力的冲击系数对比分析发现，吊杆冲击系数较小．

3.3 车重对冲击系数的影响

车重的不同会影响桥梁结构的静力响应，而车重的增加将导致行车车辆自振频率的增大，从而影响桥梁结构的动力响应，因此对桥梁各构件的冲击系数必然产生一定的影响．分别计算车重不同时桥梁结构各部位构件的冲击系数，计算结果如图12所示．

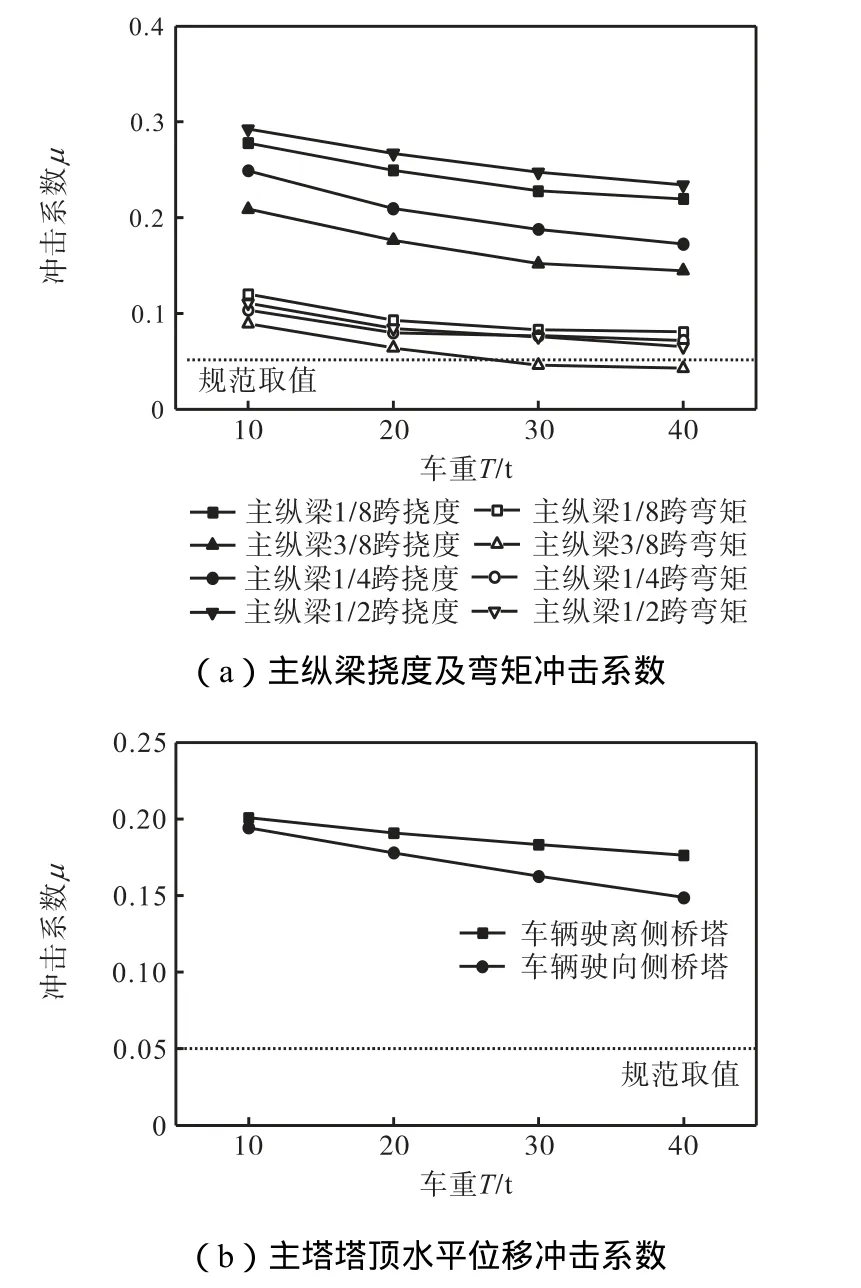
图12 冲击系数随车重变化曲线Fig.12 Variation of impact coefficient with vehicle weight

由图 12可见，随着车重的增加，各构件冲击系数均减小．主纵梁各截面挠度冲击系数均明显大于弯矩冲击系数，且两者减小幅度随车重的增加而明显降低，这主要是因为，车重增加导致桥梁结构各构件静力响应增大，但动力响应增大较小，汽车运行更加平稳，桥梁所受的动力冲击作用减弱．通过分析计算可知，当车重由10t变化至40t时，主纵梁各截面挠度冲击系数平均减小 25%，同时，主纵梁各截面挠度平均增大 220%，因此即使冲击系数随车重增大而减小，也要对行车车重进行严格限载．车辆驶向侧桥塔的冲击系数明显低于驶离侧桥塔，且随着车重的增加，驶向侧桥塔冲击系数减小幅度大于驶离侧桥塔．

3.4 横向加载位置对冲击系数的影响

汽车行驶在桥面单侧时，桥梁中心线两侧对称的构件所受的冲击作用必然有所不同，而横向加载位置的变化也会导致桥梁各构件动力冲击作用随之改变[15]．为研究横向加载位置对结构各构件冲击作用的影响，根据实际车道位置不同分别计算汽车行驶时主纵梁的冲击系数，车辆沿车道横向加载布置见图3(a)．

限于篇幅原因，仅选取 1/8跨及跨中截面主纵梁冲击系数进行分析，其挠度冲击系数随横向加载位置的变化曲线如图 13所示．由图 13(a)跨中截面各纵梁挠度冲击系数及图 13(b)1/8跨截面各纵梁挠度冲击系数分析可知，随着汽车逐渐向主纵梁Ⅰ偏载，两侧主纵梁挠度冲击系数变化幅度较大，中间次纵梁挠度冲击系数变化幅度很小，说明汽车偏载对两侧主纵梁的冲击系数影响更明显；其中主纵梁Ⅰ挠度冲击系数逐渐减小，次纵梁Ⅱ挠度冲击系数先增大再减小，次纵梁Ⅲ、主纵梁Ⅳ挠度冲击系数逐渐增大．可见，对各纵梁而言，随着车辆荷载的靠近，挠度冲击系数减小，随着车辆荷载的远离，挠度冲击系数增大．同时，即使偏载严重，两侧主纵梁挠度冲击系数也要大于中间次纵梁挠度冲击系数．

由图 13(c)偏载侧主纵梁Ⅰ挠度冲击系数随横向加载位置变化曲线可知，随着车辆偏载距离的增大，偏载侧主纵梁的各截面冲击系数均减小，且减幅均逐渐降低．由图 13(d)远离车载侧主纵梁Ⅳ挠度冲击系数随横向加载位置变化曲线可知，随着车辆偏载距离的增大，非偏载侧主纵梁的各截面冲击系数均增大，且增幅均逐渐升高．由图可知，当汽车加载位置由沿桥梁中心线变至距中心线9.75m，偏载侧主纵梁挠度冲击系数平均减小 30%左右，远离荷载侧主纵梁挠度冲击系数平均增大 120%左右，车辆偏载对远离车载侧的主纵梁挠度冲击系数影响更大．

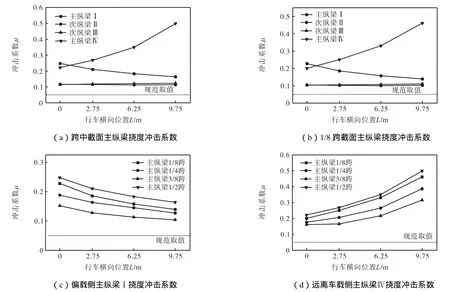
图13 冲击系数随横向加载位置的变化Fig.13 Variation of impact coefficient with lateral loading position

3.5 影响因素敏感性分析

在考虑车辆特性及桥面不平顺的情况下，分析可得悬索桥各构件冲击系数呈现明显的非线性．据上述计算结果，对各构件冲击系数随各因素(行车速度v、桥面不平顺等级D、车重T、横向加载位置L)变化的数据进行极差分析[4]，结果如表4所示．

表4 冲击系数极差分析Tab.4 Differential analysis of impact coefficient

由表4及上述各工况计算分析结果可见，对于该大跨度悬索桥，有以下3点：

(1) 对主纵梁截面而言，其挠度冲击系数的各因素影响极差范围为 0.047～0.351，弯矩冲击系数的各因素影响极差范围为 0.022～0.176，对同一截面而言，挠度冲击系数与弯矩冲击系数的变化程度不同，大多数工况下，弯矩冲击系数小于挠度冲击系数；

(2) 主塔塔顶水平位移冲击系数受各因素影响的极差范围为 0.010～0.130，吊杆轴力冲击系数受各因素影响的极差范围为 0.011～0.085，各构件冲击系数受各因素影响程度的大小排序为：主纵梁＞主塔＞吊杆；

(3) 因速度影响的冲击系数极差范围是 0.015～0.149，因桥面不平顺影响的冲击系数极差范围是0.082～0.0.351，因车重影响的冲击系数极差范围是0.011～0.077，因横向加载位置影响的冲击系数极差范围是 0.010～0.089，各构件冲击系数影响因素的敏感性排序为：桥面不平顺度＞行车速度＞横向加载位置＞车重．

4 结 论

(1) 数值分析结果表明，依据《公路桥涵设计通用规范》(JTG D60—2015)规定，在计算大跨度悬索桥汽车冲击系数时，仅考虑桥梁基频得到的冲击系数是偏于不安全的．

(2) 随着行车速度的增加，位移冲击系数变化趋势较弯矩及轴力冲击系数变化更明显，其中车速对冲击系数的影响主要与桥梁各构件的卓越振动频率有关，当卓越振型与自振竖弯振型频率接近时，汽车对桥梁的冲击作用显著增加．

(3) 桥面不平顺度对悬索桥的动力响应有明显影响，采用车桥耦合振动分析并考虑桥面不平顺度后计算的冲击系数大于我国 15规范规定值，建议后续规范规定中适当考虑桥面不平顺度的影响；当桥面逐渐恶化后，各构件冲击系数增幅极大，其中对主纵梁的影响明显大于对吊杆与主塔的影响．

(4) 车重对桥梁构件冲击系数影响较小，各构件冲击系数随车重的增加逐渐降低，并且降低幅度逐渐变小．同时，车重增大使纵梁各截面挠度变大，因此考虑整体计算，要对通行的行车车重进行严格限制．

(5) 横向加载位置的变化对横桥向各纵梁挠度冲击系数的影响大于对单一纵梁顺桥向各截面冲击系数的影响；对同截面各纵梁而言，随着汽车荷载的靠近，冲击系数减小，随着车辆汽车的远离，冲击系数增大；偏载侧纵梁顺桥向各截面挠度冲击系数随加载位置偏离桥梁中心线距离的增大而减小．

(6) 影响桥梁冲击作用的多种因素敏感性不同，各构件冲击系数影响因素的敏感性排序为：桥面不平顺度＞行车速度＞横向加载位置＞车重．为了制定适合实际运营情况的公路悬索桥的检测、养护标准，仍需要积累更多的统计数据，并开展深入研究．

[1] 中交公路规划设计院.JTG D60—2015 公路桥涵设计通用规范[S].北京：人民交通出版社，2015.

CCCC Highway Consultants.JTG D60—2015 General Code for Design of Highway Bridges and Culverts[S].Beijing：China Communications Press，2015(in Chinese).

[2] 王 达，韩万水，黄平明，等.桥面平整度对大跨度悬索桥车桥耦合振动的影响[J].长安大学学报：自然科学版，2009，29(4)：53-58.

Wang Da，Han Wanshui，Huang Pingming，et al.Influence of bridge surface roughness on vehicle-bridge coupled vibration of long-span suspension bridge[J].Journal of Chang’an University：Natural Science Edition，2009，29(4)：53-58(in Chinese).

[3] 王小松，崔建功.大跨度悬索桥冲击系数研究[J].重庆交通大学学报：自然科学版，2013，32(增 1)：848-851.

Wang Xiaosong，Cui Jiangong.Impact coefficient of long-span suspension bridge[J].Journal of Chongqing Jiaotong University：Natural Science，2013，32(Suppl1)：848-851(in Chinese).

[4] 周勇军，赵 煜，贺全海，等.刚构-连续组合桥梁冲击系数多因素灵敏度分析[J].振动与冲击，2012，31(3)：97-101.

Zhou Yongjun，Zhao Yu，He Quanhai，et al.Mutiparameters sensitivity analysis of impact factors for rigidcontinuous combined bridge[J].Journal of Vibration and Shock，2012，31(3)：97-101(in Chinese).

[5] 王贵春，陈卫丽.基于车桥耦合振动的大跨度斜拉桥冲击系数研究[J].公路工程，2015，40(6)：119-124.

Wang Guichun，Chen Weili.The study on the impact factor of highway cable-stayed bridge with long span on the basis of vehicle-bridge coupled vibration[J].Journal of Highway Engineering，2015，40(6)：119-124(in Chinese).

[6] 朱劲松，邑 强.中下承式拱桥吊杆应力冲击系数不均匀性研究[J].振动与冲击，2012，31(13)：5-10.

Zhu Jinsong，Yi Qiang.Non-uniformity of stress impact coefficient of suspenders on half-through or through arch bridge[J].Journal of Vibration and Shock，2012，31(13)：5-10(in Chinese).

[7] Lei G，Moe S C.Computer simulation of dynamic interaction between vehicle and long span box girder bridges[J].Tsinghua Science and Technology，2008，13(S1)：71-77.

[8] Au F T K，Cheng Y S，Cheung Y K.Effects of random road surface roughness and long-term deflection of prestressed concrete girder and cable-stayed bridges on impact due to moving vehicles[J].Computers and Structures，2001，79(8)：853-872.

[9] 卜建清，娄国充，罗韶湘.汽车对桥梁冲击作用分析[J].振动与冲击，2007，26(1)：52-64.

Bu Jianqing，Lou Guochong，Law Siuseong.Analysis of impact effects of moving vehicles on a continuous bridge[J].Journal of Vibration and Shock，2007，26(1)：52-64(in Chinese).

[10] 逄焕平，王建国，钱 锋.大跨度悬索桥的车桥耦合振动分析[J].合肥工业大学学报：自然科学版，2011，34(1)：114-118.

Pang Huanping，Wang Jianguo，Qian Feng.Analysis of vehicle-bridge interaction of long span suspension bridges[J].Journal of Hefei University：Natural Science Edition，2011，34(1)：114-118(in Chinese).

[11] 张 鹤，张治成，谢 旭，等.月牙形多拱肋钢管混凝土桁架拱桥动力冲击系数研究[J].工程力学，2008(7)：118-124.

Zhang He，Zhang Zhicheng，Xie Xu，et al.Theoretical study on the impact factor of crescent-shaped multirib concrete filled steel tube truss arch bridges[J].Journal of Engineering Mechanics，2008(7)：118-124(in Chinese).

[12] 霍学晋，蒲黔辉.蝶形拱桥的动力冲击系数研究[J].振动与冲击，2014，33(1)：176-182，208.

Huo Xuejin，Pu Qianhui.Impact factors of butterflyshaped arch bridges[J].Journal of Vibration and Shock，2014，33(1)：176-182，208(in Chinese).

[13] 王贵春，张校卫.考虑车辆运行参数变化的悬索桥车激振动分析[J].铁道科学与工程学报，2017，14(7)：1442-1448.

Wang Guichun，Zhang Xiaowei.The analysis on vehicle-excited vibration of suspension bridge considering variation of vehicle operational parameters[J].Journal of Railway Science and Engineering，2017，14(7)：1442-1448(in Chinese).

[14] 郝向炜，张 志，李 岩，等.考虑桥面随机不平度的钢管混凝土拱桥冲击系数统计分析[J].公路交通科技，2017，34(3)：80-86.

Hao Xiangwei，Zhang Zhi，Li Yan，et al.Statistical analysis on impact factor of CFST arch bridge considering random roughness of bridge deck[J].Journal of Highway and Transportation Research and Development，2017，34(3)：80-86(in Chinese).

[15] 冀 伟，邓 露，何 维，等.波形钢腹板 PC简支箱梁桥局部与整体动力冲击系数的计算分析[J].振动与冲击，2017，36(8)：22-28.

Ji Wei，Deng Lu，He Wei，et al.Local and global impact factors analysis for PC box girder bridges with corrugated steel webs[J].Journal of Vibration and Shock，2017，36(8)：22-28(in Chinese).