基于肺部CT影像的针道识别关键技术研究

鲍 潮，姜 杉，张国彬，杨志永

(天津大学机械工程学院，天津 300350)

在我国，肺癌一直是发病率和死亡率最高的癌症[1]．作为放射治疗重要分支之一，近距离粒子放射治疗由于其治疗时间短、剂量控制率高等优点被广泛用于众多部位癌症的治疗，例如肺部、肝部、前列腺等部位[2-4]．近距离放射治疗是在医学图像(MRI、CT、US等)引导下，将所有放射性粒子通过空心穿刺针植入到病人病变组织内，借助粒子的放射性以达到杀死癌细胞的目的．手术前要求物理师根据病人影像在治疗计划系统(treatment planning system，TPS)上制定出最优的治疗计划，在术后根据植入粒子后的影像判断治疗效果[5]．

将所有粒子放置在术前计划位置以保证最优剂量分布是近距离手术成功的关键．然而由于针刺入过程中多种因素的存在，如肿瘤肿胀、组织变形、针变形等导致术前计划并没有很好地在术中执行．这种亚优化的剂量分布不仅会影响治疗效果还会对肿瘤周围重要器官造成威胁，因此，为了解决术前计划失效问题，本文提出一种基于CT图像的自动针道识别技术．有了术中实际的针道位置，术前计划中的理想粒子便可以根据其术前所属的针全部导入到术中对应的实际针路径上，通过调整粒子位置和数量便可以获得一个最优的术中剂量计划以指导粒子植入．

由于术中实际针道位置对医生来说非常重要，很多学者都对此进行了研究．Barva等[6]利用最大化并行积分投影算法并且联合分层网格加速技术实现了电极轴的提取．尽管该方法实现了较高的精度，但是由于其较长的处理时间(MATLAB上运行10min左右)导致在临床上并不是一个实际的手段．为了改进上述问题，Uhercik等[7]提出一种多分辨率的并行积分投影算法，实现电极轴快速定位的同时且保持相同的精度．Qiu等[8]使用三维霍夫变换算法在实际病例数据中实现了1mm的针尖定位误差且运行时间是2s．而后通过对霍夫变换进行改进，Qiu等[9]又提出在粗分辨率下进行随机霍夫变换，将算法运行时间减少至1s．Okazawa等[10]将霍夫变换推广到超声图像中曲线针识别问题．Ding等[11]通过两幅正交投影图像获取三维超声图像中针的位置信息．Yan等[12]还提出利用形状信息和水平集技术也能够成功分割出针道.

上述算法各有优势，但是这些算法也存在一些缺陷，例如对干扰非常敏感、计算复杂且只关注于单针的分离．为了解决现有算法中所存在的这些问题，本文提出一种更加稳定、高效的针道检测算法．该算法通过结合图像预处理技术与改进的随机样本一致性(random sample consensus，RANSAC)算法实现了针形状的近似．在 RANSAC算法中，利用预检验技术加速了原始算法的迭代过程从而提高了针分割的效率．与此同时，利用局部 RANSAC[13]和主成分分析(principal component analysis，PCA)[14]相结合的措施保证了分割的精度．此外，通过循环淘汰最优模型的局内点实现了一张切片上多针的分离．最后，该算法通过模拟数据及病例数据得到了全面的验证．

1 材料与方法

1.1 材 料

本文所用到的肺癌近距离粒子植入手术病例均由天津医科大学第二附属医院提供．所用的 18G植入针为日本 HAKKO有限公司制造．算法是在一台配置为Intel(R)Core(TM)i3-2120 3.30GHz的计算机上运行，使用软件为MATLAB．

1.2 方 法

1.2.1 感兴趣区域自动提取

在进行术中针道识别步骤之前，每张CT片子上肿瘤所在区域都已经由物理师勾画好了，即每张切片上的肿瘤区域信息是已知的．正是基于此，才有了本文的感兴趣区域(region of interesting，ROI)自动提取方法：首先根据每张切片上肿瘤边界信息求出包裹肿瘤最小边界的矩形，而后将矩形整体扩大 5mm以保证所有的针道信息都在 ROI内，如果还有未包含的针道信息则忽略．最后将扩大后矩形所包括的区域从原图像中剪裁下来就得到了所述的ROI．

1.2.2 图像预处理

为了提高植入针与周围背景组织的对比度，本文在ROI引入了一个灰度映射函数．该函数为

式中：if是转换后像素点的灰度；i是转换前像素点的灰度；ilow_in和ihigh_in分别是输入图像的最小和最大灰度值；ilow_out和ihigh_out分别是输出图像的最小和最大灰度值；为转化参数．if、i、ilow_in、ilow_out、ihigh_in、ihigh_out代表的都是归一化的灰度值，范围在 0～1之间．该函数的意义就是把原图像灰度进行映射得到新图像的过程．原图像中灰度值低于ilow_in的像素点转换后被赋予了灰度值ilow_out，同理灰度值高于ihigh_in的像素点在转换后图像中灰度值为ihigh_out．而参数定义的则是中间灰度值的转化形式．当≤1时，靠近ilow_in附近低灰度变化范围被拓宽，靠近ihigh_in附近高灰度变化范围被压缩；同理，当时，低灰度变化范围被压缩，而高灰度变化范围则被拓宽．在本文中，ilow_in和ihigh_in分别被设置为 0.15和 1.00．输出图像的灰度范围设置为[0，1]．被赋值为1.7能够拓宽高灰度值范围，从而增大针和周围组织的对比度．图1为原ROI图像和经过对比度增强后的ROI图像．

图1 对比度增强后图像Fig.1 Contrast enhanced image

经过对比度增强后能够得到感兴趣区域灰度分布直方图，见图 2(a)．基于阈值，原图像I(x)Î[0,1]可被分为两个相邻部分：Xn(针像素点)和Xb(背景像素点)，即

图2 阈值处理后图像Fig.2 Threshold processed image

式中：X是ROI内所有像素点；I(x)是某一个点的灰度值．由于不同病例对应的灰度分布不一致，因此本文的值是根据经验来确定的．经过阈值处理(式(2))后得到的结果如图 2(b)所示，灰度值高于的像素点假定为针的候选点．尽管得到了所有的针候选点，但是Xn中仍然会包含许多伪点．如何利用RANSAC算法从这些点中提取出最准确针道位置如下文所述．

1.2.3 针轴与针尖识别

假设在数据集X中有N个相互关联的数据点．RANSAC算法从X中随机抽取一个样本容量为m的子集，m为计算模型参数所需最小的数据子集，其值与模型本身定义有关．通过这个最小子集可以确定出一个模型，然后利用误差阈值检验初始数据集X并且确定该模型对应的所有局内点．此抽样和检验的过程将会重复直到满足结束的标准，也就是在一定的置信概率P下至少能够筛选出一个不包含局外点的子集所需的最小的采样次数．最后，包含局内点最多的模型就是最终模型．假设数据集中局内点的占有率为，那么选出一个正确模型概率为．此时，采样k次，k个样本数据中至少有一个局外点概率为．因此，为了保证此概率低于以下，采样次数k必须满足

通过上述步骤可以得出RANSAC算法的时间复杂度T为

式中：Tx为每次抽样所需时间；Tc为每个数据点验证模型所用的时间；N为数据集X中总数据点数．一般来说，Tx和Tc对一特定的问题来说都为定值，因此，T的大小主要取决于k和N．由式(3)可知k与及m呈指数关系．在相同的置信概率下，k和N的值会随着数据集及模型的复杂而增大．为了抑制T的增长，提出了预检验技术．

假设有n个随机样本点用于预检验，且在一定置信概率tP下，正确模型的n次实验中至少存在nf个局内点．一旦发现局内点数少于nf，则判断此模型为错误模型，不再参与后续所有数据点的检验．因此，对正确模型而言，通过预检验的概率tP为

式中为从n中抽取i个局内点的组合种类数．在实际计算时，最优的nf和Pt值是在最低Pt限制下，通过测试不同的nf以找到最大nf及其所对应的Pt值而得到．数据点是否属于局内点则是根据该点误差的标准偏差来判断[15]，即

当n≥2m时，标准偏差s可以表示为

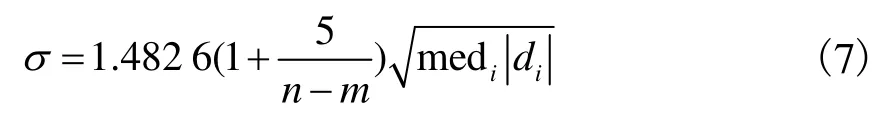
式中di为数据点的误差项，如图3所示．

图3 RANSAC算法原理示意Fig.3 Schematic diagram of RANSAC algorithm principle

在预检验步骤中，正确模型有可能被判定是错误而被剔除．因此，选出一个正确模型的概率就改变为，且此时式(3)也变为

由此可见，预检验步骤对算法效率的影响转移到了采样次数上．当Pt＜1时，相应的采样次数k要大于一般的 RANSAC算法．尽管k值有所增大，但是相比于预检验所淘汰的模型个数而言，随着k值增加而增加的模型个数是少之又少的，因为大部分的模型都被局外点所污染．这一点将会在后续实验中得到进一步的证实．

由于前面所述停止算法的条件过于理想，错误的模型也有可能获得较多的局内点，进而导致错误的识别．于是本文引入了局部 RANSAC和 PCA相结合的方法，以解决精度问题．通过预检验步骤，能够获得一个最初解以及与之相对应的内点集．所谓的局部RANSAC就是在这个亚优化内点集上进行采样和验证新模型的内点数．不同于一般性 RANSAC算法，局部 RANSAC采样是在内点集上进行，因此不需要最小化采样次数．一般来说，为了节省时间，局部 RANSAC采样数kL设置为 10～20之间．经过局部 RANSAC算法，可以得到一个优化后的模型和数据集．然而这并不是最优的模型，因为该模型的模型参数是通过采样所得的最小子集计算而来的．因此，为了获得最优的模型参数引入了 PCA算法，以最小化数据集内各点的误差．

获得最理想的针轴模型之后，针尖提取就比较容易了．方法主要是在对比度增强后的图像上沿着针轴方向对每个点灰度值进行遍历，找到灰度突变点则为针尖点．至此，针轴和针尖信息提取完毕．

1.2.4 多针提取

RANSAC算法一次只能提取一根针，为了获得一张切片上所有针道，笔者提出了连续内点删除方法．该算法首先列出所有经过当前预检验 RANSAC算法确定的最优模型所对应的局内点，然后从整体数据中移除这些被标记的点，最后使用更新后的数据进行下一轮的针道检测．正是由于数据的更新，对当前要提取的针道而言局内点的占有率也随之改变为

式中：nneedles是当前切片总针数；是图像预处理后噪声占比；nen是针对应的最多局内点数；N0是初始数据量；Nj是经过j次提取后数据点数．该连续内点删除方法会一直运行，直到找不到满足最优模型条件的样本子集为止．至此，整个识别步骤到此结束，流程如图4所示．

图4 针道识别流程Fig.4 Flow chart of needle detection

2 实验与结果

2.1 模拟数据实验

模拟数据集是由计算机生成的 1500个随机点，且每套数据集的局内点均来自于一条已知的直线．不同比例(0.1～0.8)的高斯噪声均匀地分布在指定区域．在这里给出了算法的计算时间和拾取精度，拾取精度主要指的是算法识别出的针轴和理论针轴之间的夹角．

图5(a)为本文改进的RANSAC算法(P-RANSAC)和一般性RANSAC算法(G-RANSAC)在局内点占比为 0.4时拾取结果．可以看出 P-RANSAC拾取结果更接近于理论直线．从图 5(b)可以看出 G-RANSAC算法的拾取时间随着局内点下降呈指数升高，而PRANSAC算法运行时间却只是发生了略微的增长．对于角度偏差，从图 5(c)可以看出P-RANSAC不论在何种局内点占比下都要小于 G-RANSAC，且精度一直控制在0.3°以内．

图5 模拟数据实验结果Fig.5 Experimental results of simulation data

2.2 病例实验

为了验证针道识别算法在实际图像环境中的性能，本文通过 12组肺癌病例加以验证，图 6为病例实验结果．所有病例切片层厚均为 5mm，用到的植入针均为 18G的八光针．实验中以手动分割作为参照的金标准，且识别算法在每套病例中均进行 15次以获得均值作为记录．

图6 病例数据实验结果Fig.6 Experimental results of patient data

图 6统计了所有植入针的信息识别情况．分析图 6(a)数据可以看出，超过 95%的针尖拾取误差小于 0.8mm，且最大针尖误差不超过 0.85mm．分析图6(b)数据可以看出，超过 97%的角度偏差小于 1.3°，且所有角度偏差都控制在1.4°以内．由此可见本文提出的针道识别算法的拾取精度完全满足临床要求．

此外，分析了算法的分割效率．从图 6(c)数据可以看出算法平均拾取每根针时间是 0.236s，其他各组病例的平均针道识别时间在这一值下来回波动．经统计，12组病例共植入了八光针 153根，算法成功拾取了145根，拾取率为94.78%．此外，本文对几组病例中针道识别失败的原因也进行了仔细分析．主要分为两个方面：一是由于部分病例背景像素(如肋骨等)干扰严重以及存在大量针道伪影；二是由于有些针只有很少一部分刺入了肿瘤，导致只有有限的针候选点可用于针道识别算法，这种情况经常发生在肿瘤边缘部位的针道．图 7为某病例最后拾取出的结果．

图7 某病例针道拾取效果Fig.7 Example of needle segmentation result in a patient’s case

3 讨 论

本文针对实际临床需求及相关研究现状，提出了一种基于 CT图像的、自动高效的针道识别算法，并通过模拟和实际病例实验验证了算法的性能．对于实际的病例实验，所有的针尖定位误差和针轴方向误差均被控制在0.85mm和1.4°，这种亚毫米级的精度完全满足临床近距离手术要求．而且相比于文献[8]实际病例针尖拾取精度 1mm，本文算法拾取结果要更优．此外，就针轴方向误差而言，本文实验结果要小于 2.3°(文献[16])．与此同时，算法识别整体失败率为5.22%，这对于一个随机迭代算法(RANSAC)而言是完全合理的．分割效率方面，本文提出的算法平均每根针分割时间为 0.236s，这相比于文献[7]中7.3s及文献[9]中 1.0s都要短很多，这足以说明本文算法效率是非常高的．

此外，对于肺部近距离粒子植入手术而言，在粒子植入前实现术前计划的再计划以达到最优的术中剂量分布是非常关键的．因此，本文所提出的基于CT图像的、快速精确的针道识别算法为剂量的修正提供了新思路．因为一旦所有针的实际位置都得知以后，物理师就能够将术前计划导入到术中，而后通过调整最初粒子位置或添加针以及粒子就可以改善术中剂量分布．另一方面，自动识别出的针轴方向和针尖位置可以作为一种图像测量工具被医生所使用．一旦发现针的植入位置出现较大错误，医生便可立即采取相应的措施进行补救．最后，本文所提出的算法还具有很高的灵活性，只要重新定义模型函数及其相应的误差项便可用于其他参数化目标的识别．

4 结 语

本文提出了一种改进的 RANSAC算法用于 CT图像的针道识别，该算法首先利用预检验技术加速了迭代过程，而后结合局部RANSAC和PCA算法保证了较高的精度，最后通过模拟和病例数据实验验证了该算法的性能．与此同时，所得的实验结果(较短的分割时间和亚毫米级的精度)满足临床手术的要求.在未来工作中，笔者希望一个基于自动针道识别的可靠的术中剂量优化模块能够整合到近距离放射治疗计划系统中去．

[1] 2017年中国最新癌症数据[J].中国肿瘤临床与康复，2017，24(6)：760.

Latest cancer statistics in China，2017[J].Chinese Journal of Clinical Oncology and Rehabilitation，2017，24(6)：760(in Chinese).

[2] 李任飞，王月东，闫 龑，等.125I粒子植入治疗非小细胞肺癌近期疗效评估[J].介入放射学杂志，2014，23(1)：65-68.

Li Renfei，Wang Yuedong，Yan Yan，et al.Implantation of125I seeds for the treatment of non-small cell lung cancer：Evaluation of short-term[J].Journal of Interventional Radiology，2014，23(1)：65-68(in Chinese).

[3] 黄文薮，蔡明岳，曾昭吝，等.Tace联合125I放射性粒子植入治疗肝细胞癌门静脉癌栓[J].介入放射学杂志，2015，24(6)：488-493.

Huang Wensou，Cai Mingyue，Zeng Zhaolin，et al.Transarterial chemoembolization combined with CT-guided125I seed implantation for the treatment of hepatocellular carcinoma associated with portal vein tumor thrombus[J].Journal of Interventional Radiology，2015，24(6)：488-493(in Chinese).

[4] 张丽霞，陈金燕，徐彩云，等.125I粒子植入治疗高风险局限性前列腺癌临床研究[J].浙江医学，2017，39(24)：2267-2269.

Zhang Lixia，Chen Jinyan，Xu Caiyun，et al.Efficacy of 125-iodine seeds branchytherapy for high-risk local prostate cancer[J].Zhejiang Medical Journal，2017，39(24)：2267-2269(in Chinese).

[5] Stewart A，Parashar B，Patel M，et al.American brachytherapy society consensus guidelines for thoracic brachytherapy for lung cancer[J].Brachytherapy，2016，15(1)：1-11.

[6] Barva M，Uhercik M，Mari J M，et al.Parallel integral projection transform for straight electrode localization in 3-D ultrasound images[J].IEEE Transaction on Ultrasonics，Ferroelectrics，and Frequency Control，2008，55(7)：1559-1569.

[7] Uhercik M，Kybic J，Liebgott H，et al.Multiresolution parallel integral projection for fast localization of a straight electrode in 3D ultrasound images[C]//5th IEEE International Symposium on Biomedical Imaging.USA：IEEE，2008：33-36.

[8] Qiu W，Yuchi M，Ding M，et al.Needle segmentation using 3D Hough transform in 3D TRUS guided prostate transperineal therapy[J].Med Phys，2013，40(4)：305.

[9] Qiu W，Ding M，Yuchi M.Needle segmentation using 3D quick randomized Hough transform[C]// Proc SPIE Intell Netw Intell Syst(ICNIS).USA：IEEE，2008：449-452.

[10] Okazawa S H，Ebrahimi R，Chuang J，et al.Methods for segmenting curved needles in ultrasound images[J].Med Image Anal，2006，10(3)：330-342.

[11] Ding M，Cardinal H N，Fenster A.Automatic needle segmentation in three-dimensional ultrasound images using two orthogonal two-dimensional image projections[J].Med Phys，2003，30(2)：222-234.

[12] Yan P，Cheeseborough J C，Chao K S C.Automatic shape-based level set segmentation for needle tracking in 3-D TRUS-guided prostate brachytherapy[J].Ultrasound Med Biol，2012，38(9)：1626-1636.

[13] Chum O，Matas J，Kittler J.Locally optimized ransac[C]// Lecture Notes in Computer Science.London，UK，2003：236-243.

[14] 许淑娜，李长坡.对主成分分析法三个问题的剖析[J].数学理论与应用，2011，31(4)：116-121.

Xu Shuna，Li Changpo.Dissection to three typical issues of principal component analysis[J].Mathematical Theory and Applications，2011，31(4)：116-121(in Chinese).

[15] Torr P H S，Zisserman A.MLESAC：A new robust estimator with application to estimating image geometry[J].Comput Vis Image Und，2000，78(1)：138-156.

[16] Cool D W，Gardi L，Romagnoli C，et al.Temporalbased needle segmentation algorithm for transrectal ultrasound prostate biopsy procedures[J].Med Phys，2010，37(4)：1660-1673.