船舶推进轴系纵向振动共振转换器的优化设计
胡泽超 ,何琳 ,徐伟 ,李正民 ,赵兴乾
1海军工程大学振动噪声研究所,湖北武汉430033
2船舶振动噪声重点实验室,湖北武汉430033
0 引 言
在不均匀伴流场下,螺旋桨的周期性运转产生的脉动激励力是船舶在中高速航行时的主要噪声源。该纵向激励力通过推力轴承传递至船体,会引起轴系及船体的振动,影响船舶的运行安全,降低船体的声学性能。为了减小纵向激励力向船体的传递,可在轴系上安装减振器。考虑到推力轴承传递大推力、小位移的特性,需要设计一种刚度低、阻力大的隔振装置。液压减振装置利用流体的可压缩性来调整系统的刚度和阻尼,通过合理的设计,可使推进轴系的动态特性满足指标要求。在推力轴承处安装共振转换器(Resonance Changer,RC)不仅能调节推进轴系的纵向固有频率以偏离螺旋桨的脉动激励频率,还能降低船体艉部的纵向振动响应,达到实现隔振的目的。Goodwin[1]认为,RC可等效为一种质量―弹簧―阻尼单元,据此设计了一种能在特定频段内降低轴系纵向振动的液压减振装置。Dylejko等[2]和Li等[3]利用传递矩阵法建立了桨―轴―艇体系统的数学模型,分析了RC的主要参数对桨轴系统力传递率的影响。李良伟等[4]和王珺等[5]运用动力谐调消振理论对RC进行了优化设计,得到了RC的最优固有频率比和阻尼比,但分析模型较为简单,应用范围有限。
本文拟建立桨轴系统纵向振动的力学模型,采用传递矩阵法,计算螺旋桨激励力传递到壳体的振动响应;以力传递率为指标,分析RC的活塞缸直径d0,连接管长度l1和直径d1及油箱体积V1的变化对桨轴系统隔振效果的影响,分别采用力传递率最大值最小化方法和力传递率与坐标轴围成的面积最小修正法,对RC的主要参数进行优化设计。
1 RC的动力学模型
RC由充满油液的油箱、外接管系和活塞缸组成,装置内的工作流体可以改变轴系的纵向刚度和阻尼[6]。图1为RC的原理模型,其中,P为活塞两侧的压力差,x0和x1为活塞缸两端的位移。

图1 RC结构简图Fig.1 Structure diagram of RC
为了便于推导RC的动力学方程,需作出如下假设[7]:
1)油箱壁是刚性的,流体的压缩全部发生在油箱内;
2)连接管内的流体处于层流状态;
3)管内的流体可视为集中质量;
4)流体的水力有效长度等于连接管的实际长度;
5)不考虑管道中的压缩效应。
根据假设条件,由D'Alembert原理可知,活塞缸内作用于连接管上的压力等于连接管中油受到的惯性力、连接管内的阻尼力以及压缩油箱内的油所需力之和,则RC的动力学方程可描述为


其中,Mh,Kh和Ch分别为RC的质量、刚度和阻尼,则可将式(2)转换成质量―弹簧―阻尼的数学模型:

式中,F0为活塞受到的外力。
2 桨轴系统纵振数学模型
桨轴系统纵向振动的力学模型如图2所示,模型可分解为5个子系统,每个子系统均可以用传递矩阵来表示元件左右两端纵向振动的传递关系。图2中,下标 p,t,c,b,h分别为螺旋桨、推力盘、联轴器、基座和RC,Mp,Mt,Mb,Mc分别为螺旋桨、推力盘、基座、联轴器的质量,K0和Kb分别为油膜和基座的刚度,C0为油膜的阻尼,Ls和Lse分别为艉轴的实际长度和有效长度,L为中间轴的长度,从螺旋桨至联轴器分别为1~5号单元,Ti(i=1,2,3,4,5)为其对应的单元传递矩阵,分别代表j单元左、右端面的位移响应和力响应,下标j可用 b,h,c,t,p替代。

图2 桨轴系统纵向振动力学模型Fig.2 Mechanical model of longitudinal vibration of propeller shafting
2.1 轴系纵振的点传递矩阵
考虑螺旋桨脉动激励力Fp的作用,桨轴系统的纵向传递矩阵应改写为T3×3的形式,式(4)~式(7)为桨轴系统各子系统的传递矩阵:

式中:k=ω c,为轴(尾轴和中间轴的材料属性及截面积均相同)的纵向波数,其中ω为角频率,,为轴的纵向波速,ρ为轴的密度;E和A分别为艉轴和中间轴的弹性模量和截面积。螺旋桨和联轴器可视为集中质量块。由于艉轴较长,计算时一般需考虑其有效长度,相应的传递矩阵为T2。
集成RC的推力轴承可进一步分解为3个单元:推力盘、油膜和RC。推力盘右端面至船体的传递矩阵方程可表示为式(8):


式中,Ke为推力盘与壳体之间的等效刚度。
根据式(9),可将推力轴承—基座—壳体模型简化为如图3所示的等效力学模型,则与集成RC的推力轴承对应的传递矩阵T3可简化为式(10):

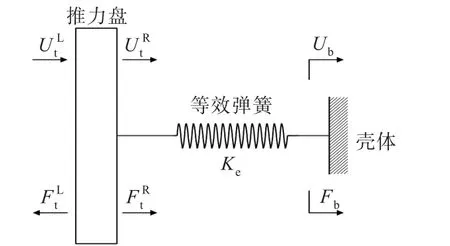
图3 推力轴承和基座的等效力学模型Fig.3 Equivalent mechanical model of thrust bearing and base
2.2 轴系纵振响应计算
在得到T1~T5各单元的传递矩阵后,依据边界条件,可对桨轴系统的振动响应进行求解。式(11)为螺旋桨输入端至联轴器输出端的传递矩阵,其中Tr,q表示T的第r行q列元素(1≤r,q≤3)。当脉动激励力Fp作用在螺旋桨上时,螺旋桨的左端面与联轴器的右端面可视为自由边界条件,将约束条件代入式(11),得

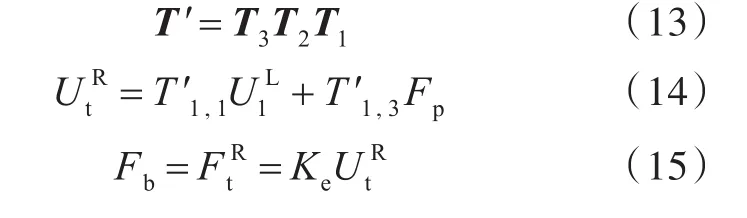
3 RC结构的优化设计方法
为了使桨轴系统具有良好的隔振效果,需要对RC进行参数设计。合理的结构参数设计能使RC装置吸收桨轴系统的大部分振动能量,可将力传递率限制在一定范围内,使共振峰值较小;还能调节桨轴系统的固有频率从而避开螺旋桨叶频激励,实现减振和调频的目的。本文以RC的l1,d0,d1和V1参数为设计目标,分别采用力传递率最大值最小化方法[9]和力传递率曲线面积最小修正法[10],对RC的结构进行优化设计。
3.1 最大值最小化优化方法
RC结构参数优化可表述为力传递率曲线峰值最大值最小化的设计问题,即通过某种算法,搜寻一组设计变量 (l1,d0,d1,V1),使桨轴系统力传递率的多个峰值在分析频率范围内取最小值。该优化方法可描述为式(16):

式中:a为纵向模态阶数;m为分析频带内力传递率峰值的个数。
最大值最小化的优化方法更关注力传递率峰值的变化情况,适用于对传递到壳体的力的幅值或对轴系强度有严格限制的约束条件的优化问题,因此,实质上是一种局部优化方法。
3.2 面积最小修正法
对于每一组设计变量 (l1,d0,d1,V1),力传递率曲线Tf(l1,d0,d1,V1)与坐标轴f围成的面积记为,该方法可描述为

4 算例分析
以某型船舶桨轴系统为例,计算的参数为:Mp=7 000 kg,Mc=1 000 kg,Mb=4 000 kg,Mt=500 kg,ρ1=860 kg/m3,ρ=7 850 kg/m3,E=200 GPa,A=0.02 m2,Ls=14.6 m,Lse=14 m,L=2 m,Kb=5×109N/m,B1=1.38 GPa,μ1=0.23 Pa·s,螺旋桨桨叶数m=7。
根据实验数据,油膜刚度K0和阻尼C0与转速n和螺旋桨所受载荷F有关。当F=200 kN时,K0和C0随转速的变化曲线如图4所示。取n=220 r/min(对应叶频为25.7 Hz),对应的K0=1.4×1010N/m,C0=6.5×108N·s/m。初步设计的RC参数为l1=1 m,d0=0.06 m,d1=0.01 m,V1=1.6 L。
令我感动的首先是这个发言的女孩子,她对好朋友的友爱和关切,在讲述的过程中,她在落泪;其次,是在场的孩子,他们所拥有的同情心—他们全都在落泪。对于一个作家来说,这个时刻是最幸福的吧,因为我看到了写作的价值所在,也看到了阅读激发了孩子们的善良和同情,在阅读中获得温暖与安慰,以及成长的勇气和力量。

图4 油膜刚度和阻尼随转速的变化曲线Fig.4 Variation curve of oil film stiffness and damping with rotating speed
RC的l1,d0,d1,V1参数对桨轴系统隔振效果的影响如图5所示。由图可知,未加RC时,桨轴系统在30和132 Hz附近出现系统前两阶共振峰,且第1阶共振峰值较大。与未加装RC系统的力传递率曲线对比,加装RC后桨轴系统的第1阶模态峰值转化成了两阶峰值更小的低阶模态,分别在未加装RC的第1阶模态频率两侧。显然,在0~200 Hz分析频带内,RC对桨轴系统的前两阶模态影响较大。
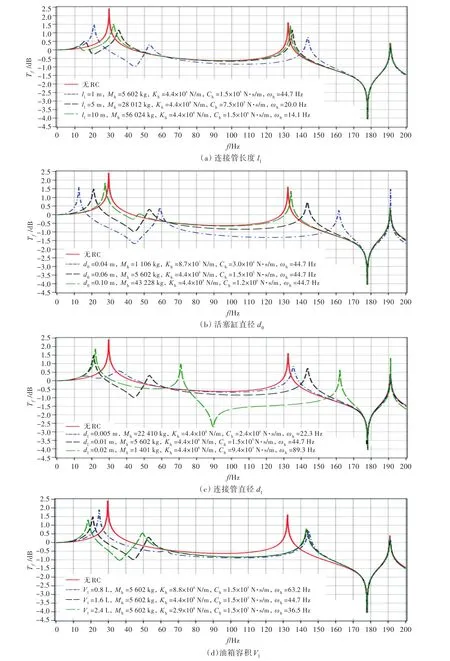
图5 RC主要参数对桨轴系统隔振效果的影响Fig.5 Influence of RC's main parameters on vibration isolation effect of propeller shafting system
根据RC的Mh,Kh,Ch和ωh频率随参数l1,d0,d1,V1的变化趋势,可得出以下结论:
1)随着l1增大,RC等效阻尼Ch增大,桨轴系统力传递率的峰值相应减小。若l1过长则会增加RC的质量,若l1过短则桨轴系统的一阶模态峰值较大。因此,必需对l1的取值范围进行约束,可约束l1∈[0.5 m, 10 m]。
2)当ωh为定值时,随着d0的增加,Kh与Mh等比例增大。若d0→∞,则RC可视为刚体,RC的力传递率将接近无RC的情况。因此,在设计RC时,d0的取值不能太大,若想获得良好的隔振效果,可设置d0∈[d1, 0.1 m]。
3)当Kh为定值时,RC的等效质量Mh随着d1的减小而增大。在设计RC时,其等效质量的设计不应过大,可限制d1∈[0 . 005 m,d0] 。
4)当Mh为定值时,V1增大相当于油箱中油层变厚,RC的刚度Kh将随之减小,隔振效果增强,但过大的V1会导致联轴器端的位移响应超过其许用范围而影响电机的正常工作,过小的V1会使力传递率曲线接近于无RC状态下的曲线,导致RC失效。为了避免上述两种现象的发生,可设置V1∈[0.8 L, 2.4 L]。
确定了RC参数的约束条件后,分别采用目标函数obj1和obj2对RC进行参数优化,优化结果见图6。由图可知:

图6 RC参数的优化结果Fig.6 Optimal results for RC parameters
1)与初始设计的RC相比,优化后RC的力传递率在分析频段内明显减小,且前三阶模态峰值均有所降低;
2)采用最大值最小化的方法能使力传递率的峰值降到最低,但无法保证RC在整个分析频带内均具有优良的隔振性能;
3)采用面积最小修正法能使RC在分析频段内具有最优的隔振性能,但不排除在某些频率处会出现较大的峰值。
对于本算例,根据优化结果,应该采用目标函数obj2对RC的参数进行优化,尽管力传递率曲线峰值相对于obj1略有增加,但优化后的RC在0~200 Hz频率范围内的隔振效果得到了明显改善。与初始设计相比,obj2的优化方法在第1阶模态处的峰值降低了约5.3倍,且避开了25.7 Hz的叶频激励力,减振调频效果明显,满足使用需求。
5 结 论
本文建立了推进轴系纵向振动的数学模型,结合实船数据,以力传递率为指标,采用传递矩阵法分析了RC的主要参数对桨轴系统隔振性能的影响,通过理论分析给出了设计参数的约束条件,基于最大值最小化方法和曲线面积最小的参数修正设计方法对RC的结构进行了优化设计,得出以下结论:
1)RC的引入消除了桨轴系统的第1阶模态,但带来了两阶峰值更小的低阶模态,分别在未加装RC第1阶模态频率的两侧,系统的第2阶模态频率向高频方向移动但峰值变化不大,对第3阶模态基本没有影响。
2)加装RC后,轴系的隔振效果得到了明显改善。
3)RC的参数对桨轴系统的隔振性能影响较大,合理设计RC结构能使系统获得良好的隔振效果。
4)与RC的初始设计方案相比,两种优化方法均能较大程度地改善桨轴系统的隔振性能并使其固有频率远离螺旋桨的叶频激励频率;采用最大值最小化的优化方法能使传递到壳体的力响应峰值降到最低,而采用曲线面积最小修正的设计方法能使RC装置的在整个分析频段内的减振效果更佳。

