金属表面点蚀的稳态过程数值研究

崔静，杨帆，杨霆浩，杨广峰

中国民航大学机场学院，天津300300

0 引 言

现代舰船装备结构的系统化和复杂化程度越来越高，在舰船上使用的新材料也越来越广泛，因此舰船的腐蚀防护工作面临着巨大挑战。金属腐蚀会导致舰船装备的损坏，造成经济损失以及腐蚀污染。预测腐蚀的损伤过程，对于保证舰船装备的安全和正常运行起着重要的作用。舰船所处的海洋环境复杂，运用实际测量和经验估算等方法对舰船材料表面腐蚀进行检测时，评估标准不统一，不能实时观测腐蚀发展过程，而采用计算机技术进行数值模拟，在一定程度上可弥补传统方法的不足。

腐蚀过程是一个包含了多组分之间的质量传输、化学反应或电化学反应、界面动力学等多重因素影响的复杂过程，而格子Boltzmann方法（Lattice Boltzmann Method，LBM）作为一种介观方法（Mesoscopic technique），近年来发展迅速，成功地应用于多种微观相互作用的流体系统问题中。LBM既能兼顾实际的计算成本，又能保证模型或方法的合理性。国内外运用LBM进行腐蚀模拟的研究较少，更多学者采用的是元胞自动机模型（Cellular Automata Model，CAM）进行腐蚀模拟，采用CAM进行腐蚀模拟对于多组分之间的质量传输和腐蚀化学反应只进行了简单的元胞转化，并没有理论支撑。He等［1］首次将化学反应与LBM结合，解决了流体—壁面表面反应与扩散问题的耦合。Kang等［2-3］对溶解沉淀问题中单相流体和多相流体的传输及流动进行了研究，将LBM与结点体积法（Volumn of Pixel，VOP）结合来模拟物质的传输过程。Chen等［4］为了解决多相流动中的相变和溶解沉淀问题，将LBM和VOP方法在孔隙尺度下相结合，解决了多相流中的相分离、化学反应、质量传输和溶解沉淀等问题。张婷等［5］使用MRT-LBM来模拟腐蚀溶液的流动，并分析了不同参数对腐蚀的影响。Liu等［6］使用D3Q19模型模拟了岩石的腐蚀情况。Zhang等［7］在腐蚀模型中加入了电场并与流场成功耦合，更好地模拟了电化学腐蚀。但是，现有的格子Boltzmann（LB）腐蚀模型中，并未对具体的金属材料进行模拟，更多是使用化学腐蚀的方法进行研究，仅考虑了阳极固体腐蚀，很少涉及阴极反应的发生。

本文将针对现有LB腐蚀模型的不足，采用阴阳极共同作用的方式研究电化学腐蚀，将使用改进后的模型对金属表面点蚀现象的稳态过程进行模拟，得到点蚀坑的形貌变化特征以及各组分浓度的变化情况。通过数值模拟，分析腐蚀化学反应速率、腐蚀溶液扩散系数、腐蚀产物扩散系数对腐蚀程度的影响。

1 格子Boltzmann腐蚀模型

腐蚀过程包含多相多组分的流动与扩散、电化学反应、金属的溶解以及腐蚀产物沉淀。根据以上问题建立多个子模型，并将子模型耦合形成LB腐蚀模型。其中，子模型包括电化学反应模型、多组分模型、质量传输模型、固体边界迁移模型和结点钝化模型。

1.1 电化学反应模型

模拟浸没于液体腐蚀环境的金属（以不锈钢为例）表面的点蚀现象，其腐蚀过程如图1所示。

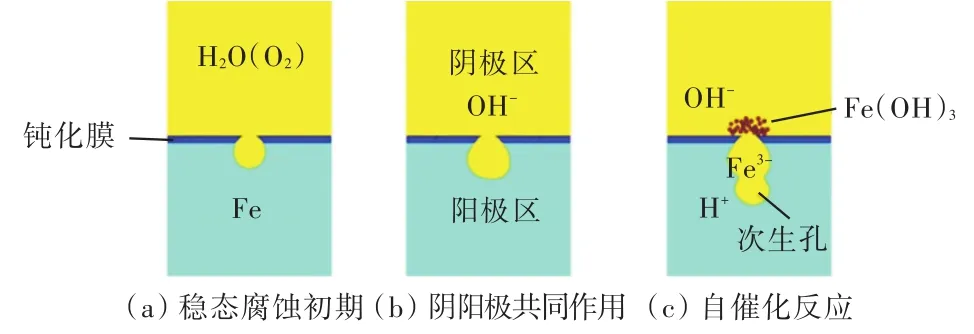
图1 物理模型示意图Fig.1 Schematic illustration of corrosion model

为了便于数值建模，本文将复杂的电化学反应过程进行如下简化。

阳极：

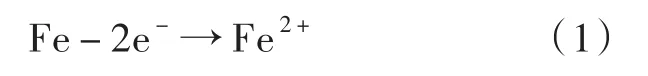
阴极：

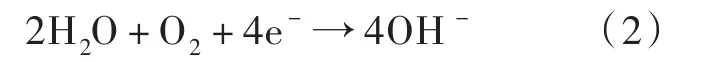
沉淀反应：

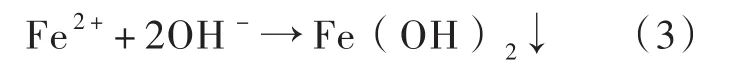
沉淀氧化：

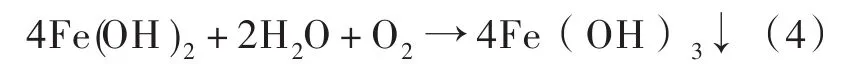
亚铁离子氧化：

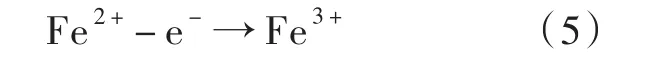
铁离子水解：

自催化反应：

假设腐蚀环境已达到蚀孔可发生稳态点蚀时（腐蚀深度达到一定值，腐蚀产物溶度达到其饱和浓度的 60%～80%［8］），如图1（a）所示。蚀孔内金属基体处于活化溶解状态，作为阳极，蚀孔外钝化膜作为阴极，孔内外形成了“大阴极，小阳极”的电化学腐蚀体系，阴阳极发生式（1）和式（2）的反应，如图1（b）所示；由于孔外发生式（2）反应，孔口处OH-逐渐增多，孔内的金属离子向孔外扩散，发生式（3）和式（4）的反应，在孔口附近产生沉淀；随着孔内金属不断腐蚀溶解，金属离子逐渐增多，继而发生式（5）的水解，孔内H+增多，呈酸化环境，进一步加快式（6）的腐蚀，如图1（c）所示。

1.2 多组分模型

使用Shan-Chen模型［2-4］来处理多组分介质间的流动，其演化方程为

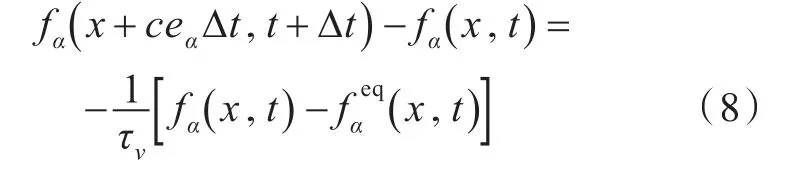
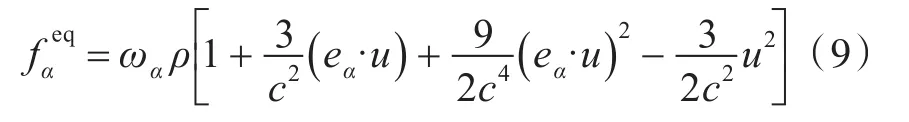
式中：ωα为权系数，ω0=4/9，ω1-4=1/9，ω5-8=1/36；宏观量密度ρ和速度u可由密度分布函数求得：

在Shan-Chen模型中，为了降低误差和保证计算结果的稳定性，使用了分子作用力对速度进行修正，分子间的作用力计算如下：

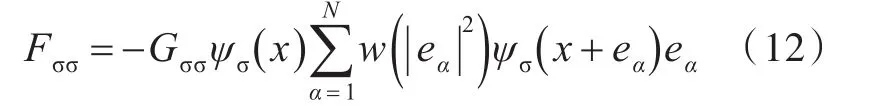
式中：Fσσ为液体分子间的作用力；Gσσ为作用强度；ψσ为有效密度函数［9-12］；为权系数，其中

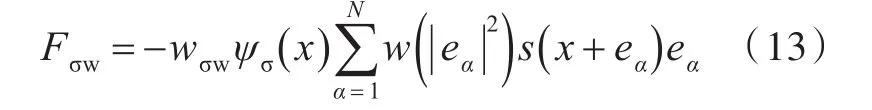
式中：Fσw为液体分子与固相分子之间的作用力；wσw为液体与固体壁面的作用强度，可通过接触角的变化进行调整；s为固体壁面密度［13-15］，与通过分布函数算出的密度不是同一概念。

将上述计算得到的分子间作用力代入下式进行速度修正：

式中：Fσ为该结点所受到的合力；u′为式（11）所求的速度；式（14）计算的u需代入式（9）进行平衡分布函数的计算。

1.3 质量传输模型

采用质量传输模型来解决溶液组分之间的相互传输问题，本文涉及到的液体组分为腐蚀溶液组分和腐蚀产物组分。LB质量传输模型的演化方程为

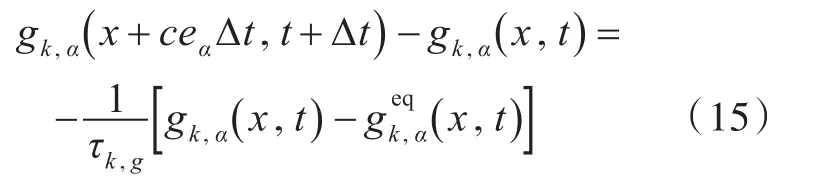
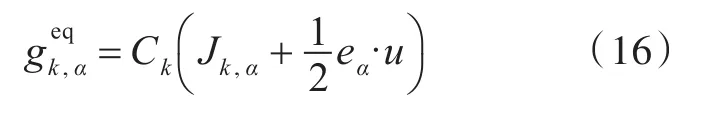
式中：Ck为第k组分的宏观量浓度；u由式（11）计算得到；系数Jk，α为

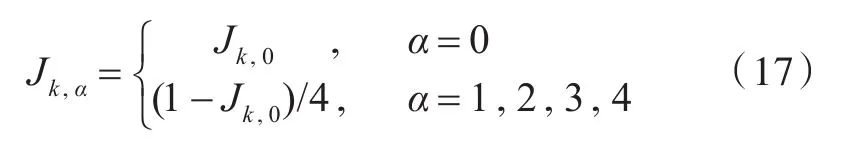
其中，Jk，0的取值范围在0～1之间。

浓度场中的扩散系数Dk为

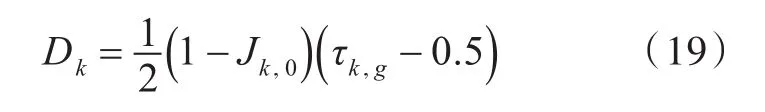
式中，Jk，0取值为0.9。

1.4 固体边界迁移模型

由于发生腐蚀溶解反应，被腐蚀的金属基体表面结点的体积会随之减小，并且当新生成的腐蚀产物浓度达到其饱和浓度时，在固体表面沉淀结点的体积会随之增大，因此，固体边界在腐蚀与沉淀的影响下不断更新。为了能更好地实时追踪新的固体边界，采用VOP方法予以解决。

根据式（1）反应，金属基体表面结点的体积变化［19］如下：

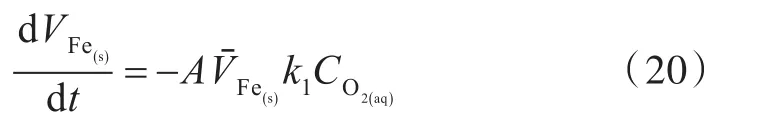
根据式（2）反应，新生成的沉淀结点在固体表面的体积变化如下：

然后我就发现，身边很多女孩跟你一样，也跟当初的我一样，总是对自己的某一个缺点耿耿于怀。见人就说：我太胖了，我腿太粗了，我眼睛太小了，我牙齿太丑了……

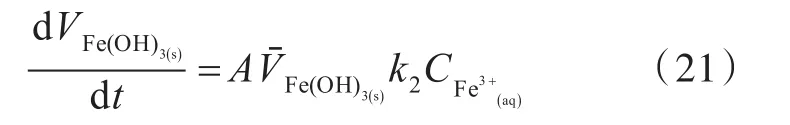
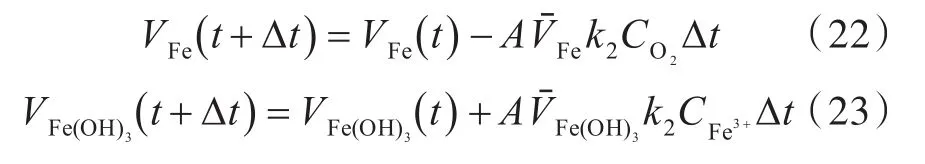
金属与腐蚀溶液在边界处发生式（1）反应的腐蚀，腐蚀边界处各组分浓度变化［7］为：

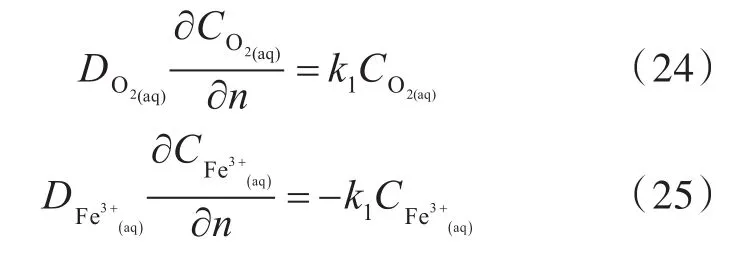
式中：CO2(aq)为腐蚀边界上O2的消耗浓度；为腐蚀边界上Fe3+的生成浓度；n为反应固体表面的外法线方向；为O2扩散系数；为Fe3+扩散系数。

1.5 结点钝化模型

模拟过程中的腐蚀边界，每个结点都有一定的概率被钝化，导致该处的腐蚀速率变慢，使腐蚀坑的形状呈现不对称性，这也符合真实的腐蚀情况。在VOP方法中，腐蚀边界处结点发生体积的变化，如果腐蚀边界某一结点发生钝化，该结点的体积减小速率会变慢。结点发生钝化的概率称为钝化概率P，钝化概率系数ε为

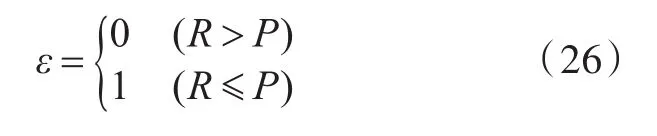
式中，R为0～1之间的任意随机实数。因此，需对式（22）进行修正：

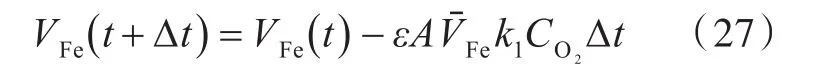
在VOP方法中引入钝化概率函数，可以避免腐蚀界面上的阳极金属受到的腐蚀作用相同，以使腐蚀坑的形貌随机变化且不对称，更加符合真实的腐蚀情况。

2 数值模拟

2.1 物理模型

基于上文构建的LB腐蚀模型，对金属表面点蚀稳态过程进行模拟。计算区域选取100×160的网格。整个计算域内，初始的初生蚀孔假设为一部分圆，其圆心位于（71，80），半径为10，钝化膜的厚度为5，如图1（a）所示。

2.2 边界条件

对于液体四周的边界采用了非平衡外推格式进行处理，而溶液与金属之间、溶液与钝化膜以及溶液与腐蚀产物沉淀之间的流动碰撞采用反弹边界进行处理。

2.3 模拟工况

本文模拟金属表面点蚀稳态过程的形貌的演化过程，参数如表1所示，表中v为运动粘度。采用变参数的数值模拟得到腐蚀程度的影响因素，各工况参数如表2所示［3，14］。所有扩散系数均由各浓度场的松弛时间决定，如式（14）所示。为了满足运行过程中的数值稳定性，选取数值需大于0.5。

表1 模拟中使用的参数Table1 Simulation parameters

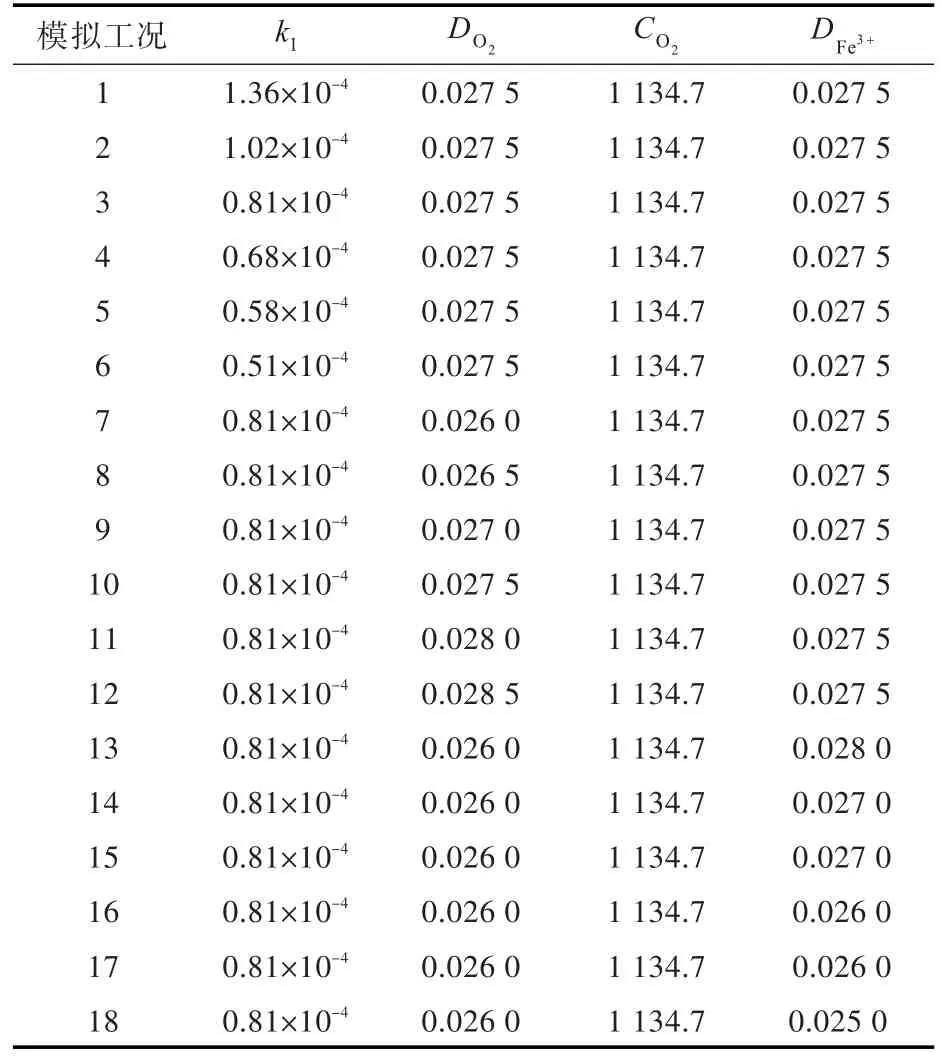
表2 模拟工况Table 2 Simulated condition

上述工况中所有参数均为无量纲参数，均通过表1中的转化关系得到。由于化学反应速率受温度、反应接触面积、催化剂等影响，且腐蚀介质扩散系数受浓度、温度等影响，这两种参数可选取值范围较广［4，15］，因此选取参数时，仅在表1中的模拟数值附近选取。

3 数值模拟结果与分析

3.1 腐蚀演化过程分析

通过模拟得到不锈钢材料表面点蚀稳态过程的形貌变化以及各组分浓度变化情况。模拟工况为k1=8.14×10-5，图2所示为不锈钢材料点蚀坑形貌随时间变化的情况。从图中可以看到，腐蚀破损区域逐渐变大，并且逐渐向金属基体纵深发展。当蚀孔出现Fe（OH）3沉淀，随着时间的推移沉淀增多，逐渐覆盖了蚀孔（图2（c））；除了初生的蚀孔发生腐蚀，在蚀孔底部出现次生蚀孔继续向金属基体深处腐蚀（图2（d）～图2（f））。

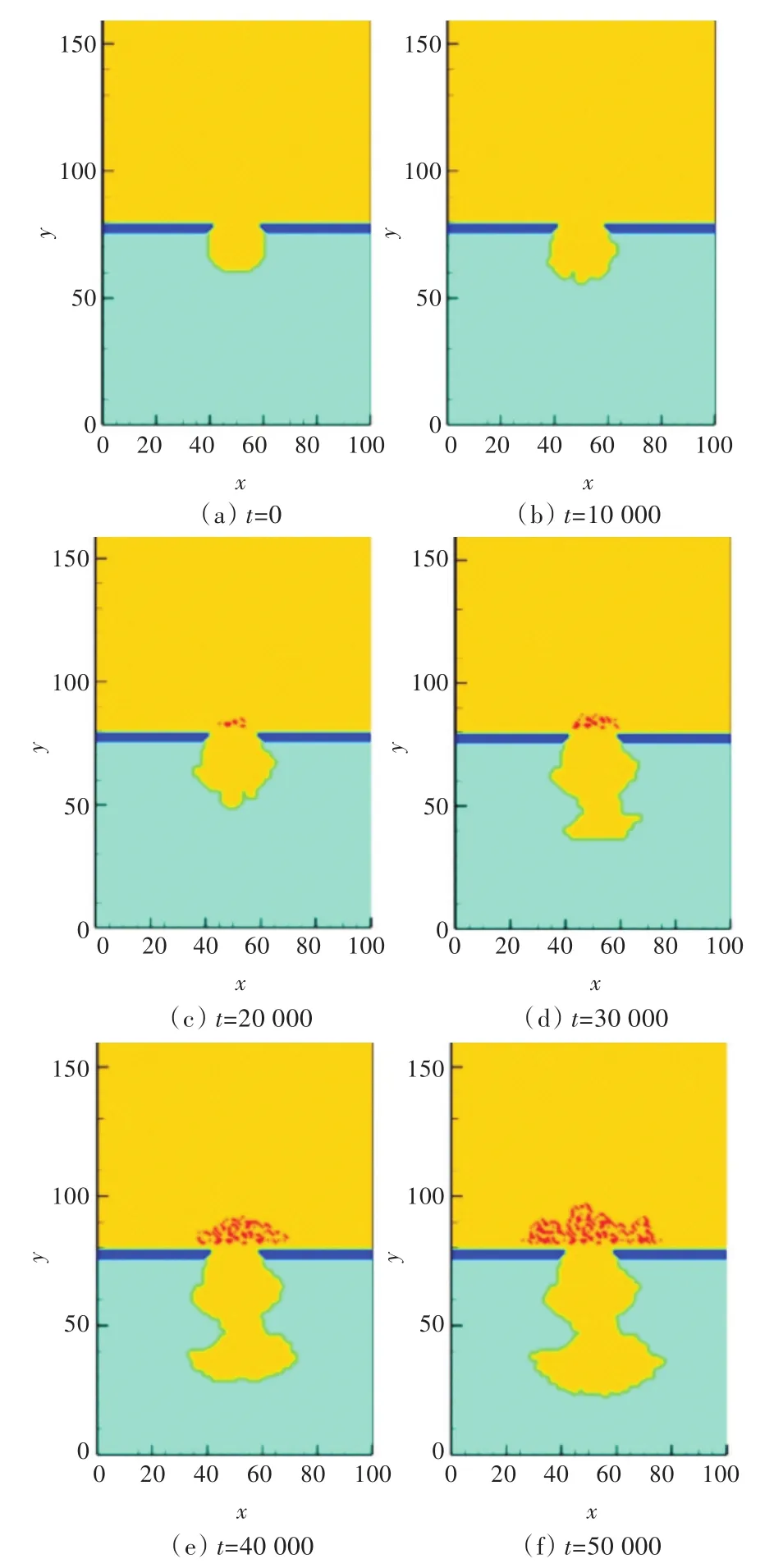
图2 腐蚀坑形状变化Fig.2 Shape evolution of corrosion pit

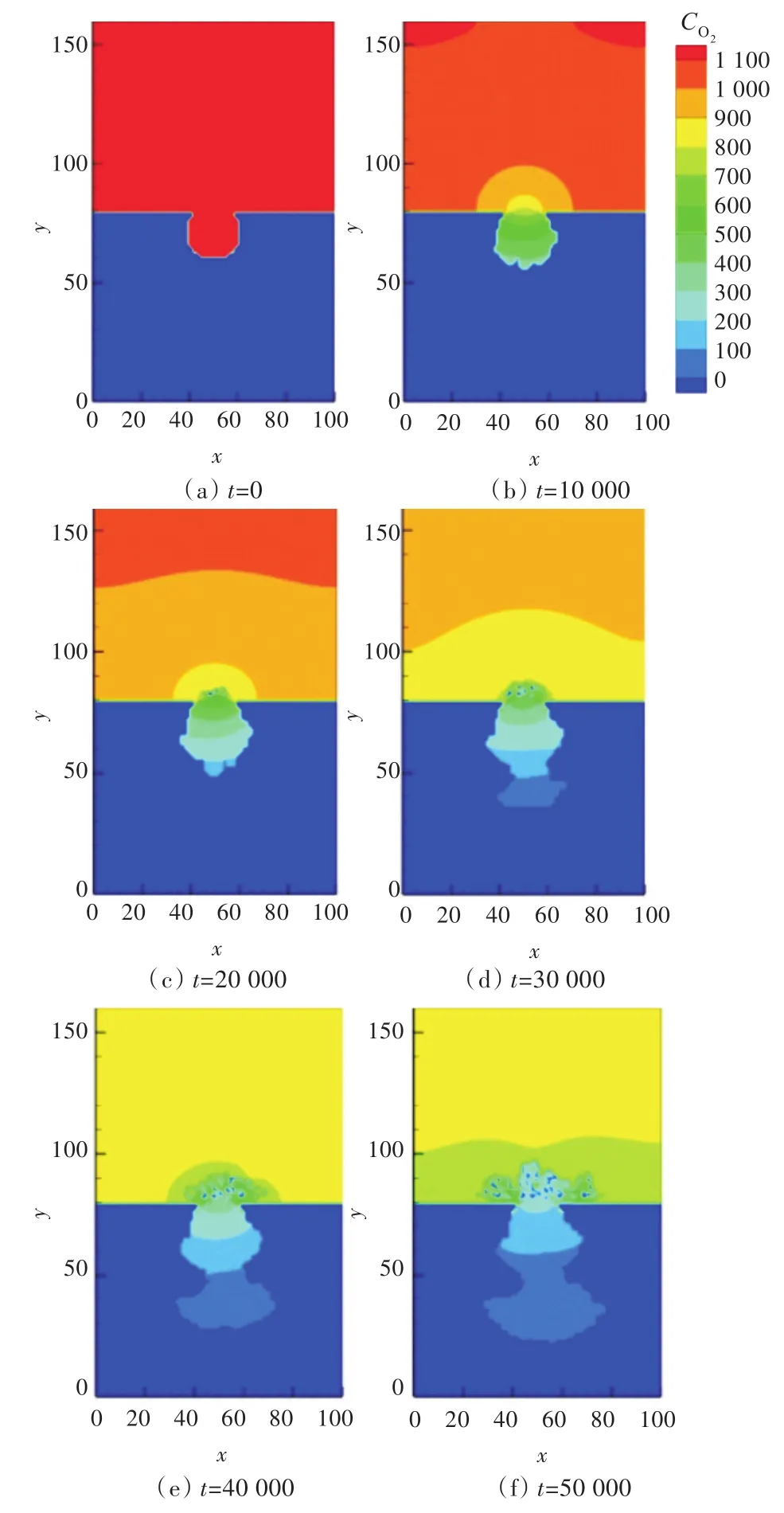
图3 腐蚀溶液浓度变化Fig.3 Change in the concentration of corrosion solution

图3所示为含氧腐蚀溶液的浓度随时间变化的情况。随着时间的延续，腐蚀的区域变大，并向金属基体纵深发展，腐蚀溶液向蚀坑内渗入，腐蚀溶液逐渐被消耗，在蚀孔处出现沉淀，阻碍了腐蚀溶液向蚀孔内扩散，导致蚀孔内腐蚀溶液的浓度逐渐降低。

图4所示为蚀孔内阳极金属发生腐蚀溶解时，腐蚀产物Fe3+的浓度变化情况。随着时间的延续，腐蚀产物在腐蚀边界不断生成，并且向蚀坑外以及液体环境扩散；当Fe3+扩散至蚀孔与孔外大量的OH-结合产生Fe（OH）3，Fe（OH）3达到其饱和浓度继而沉淀。蚀孔产生沉淀，阻碍了Fe3+向孔外扩散，孔内的Fe3+升高，导致Fe3+进一步发生水解反应。

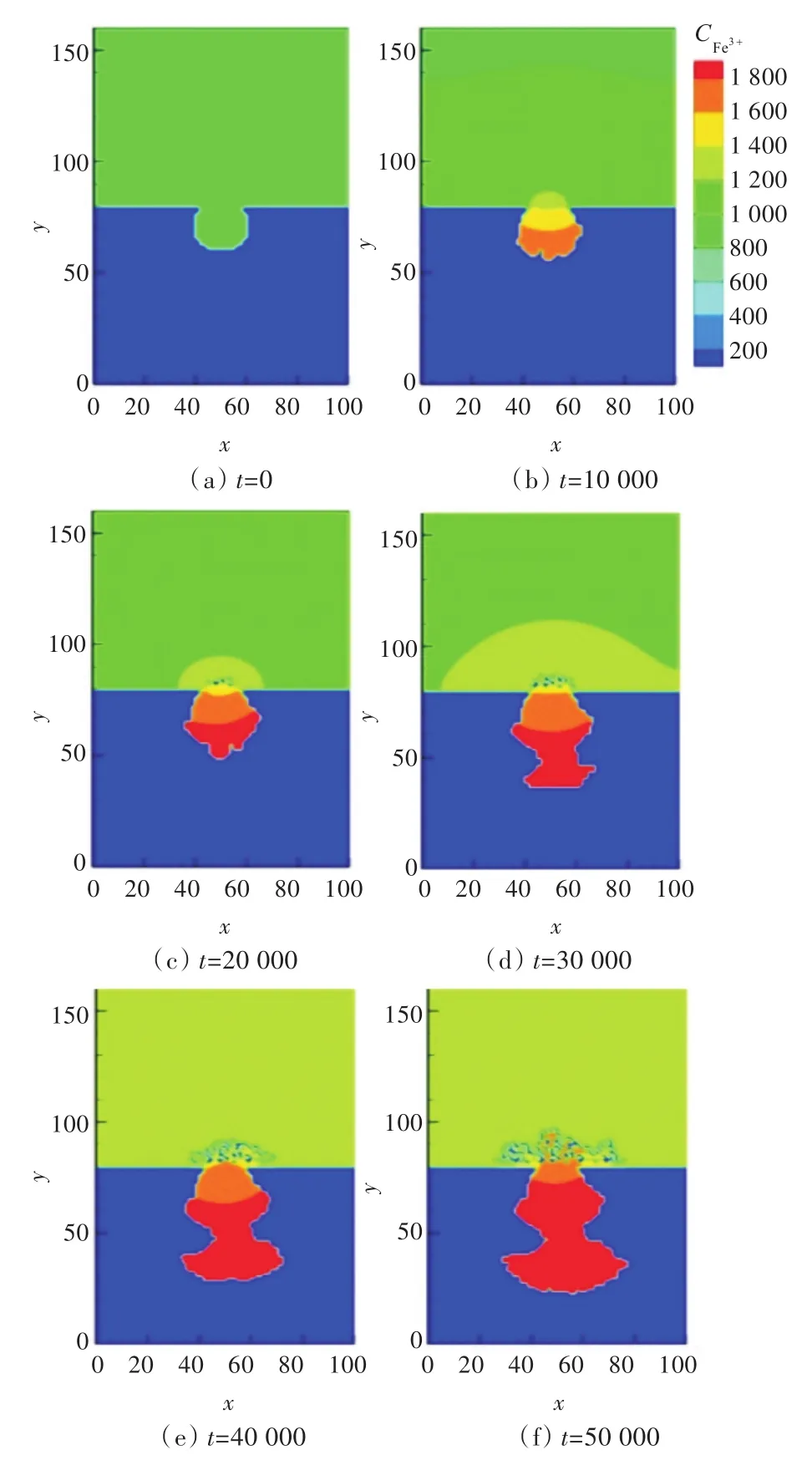
图4 腐蚀产物Fe3+浓度变化Fig.4 Changes in the concentration of corrosion products Fe3+

图5所示为蚀孔外钝化膜作为阴极及其表面产生的OH-浓度变化及OH-扩散的情况。随着时间的延续，蚀孔内阳极金属发生失电子的腐蚀溶解反应，电子通过金属基体转移至电位较高的钝化膜，O2在钝化膜表面得到电子，发生阴极反应，在表面产生大量的OH-，并向液体环境扩散；OH-扩散至蚀孔处与Fe3+生成Fe（OH）3发生沉淀反应，孔口沉淀的增多阻碍了OH-向蚀孔内的扩散，导致孔内OH-浓度降低。

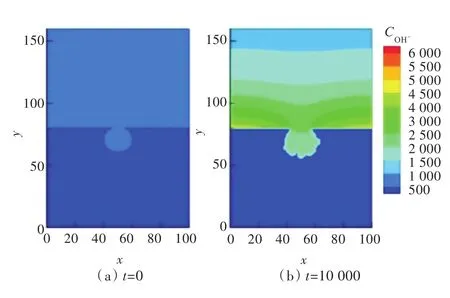
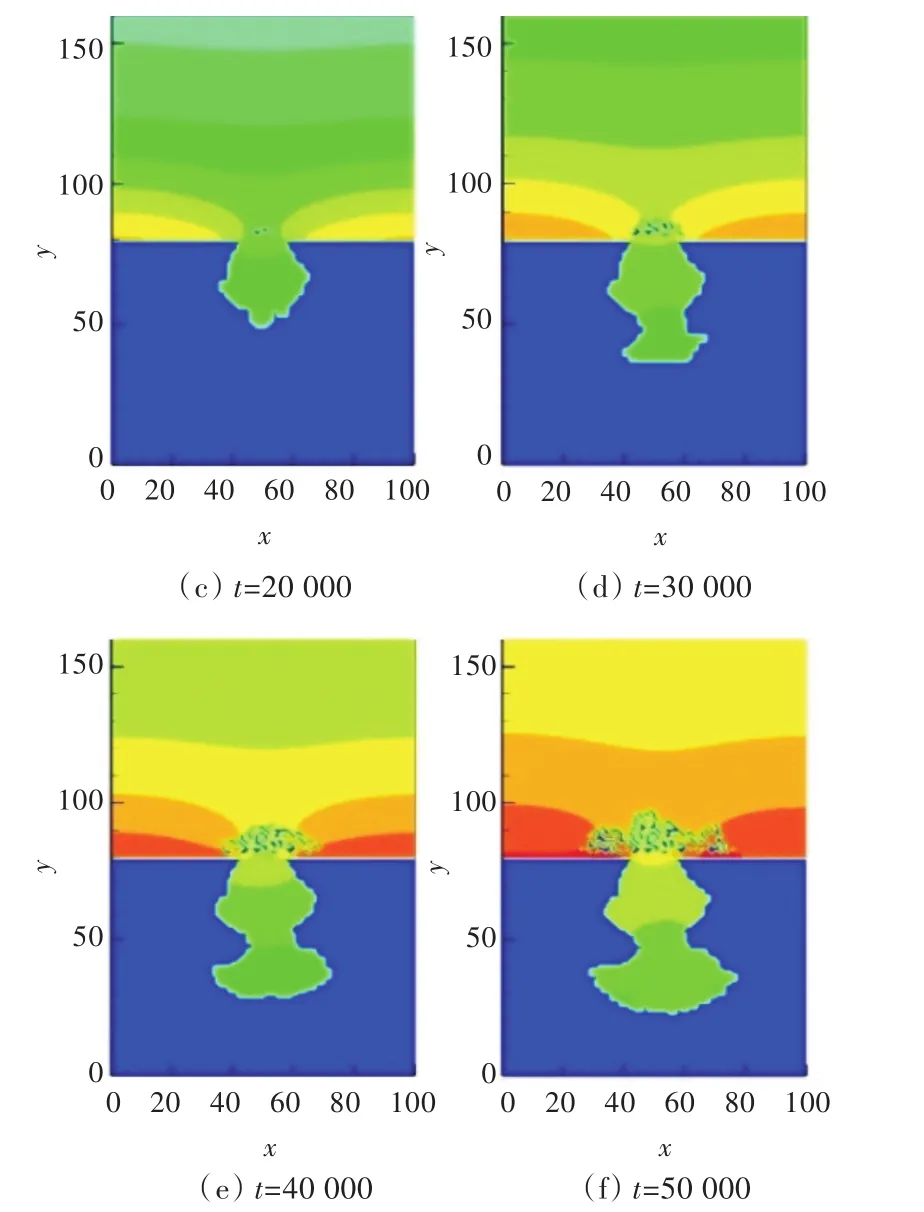
图5 OH-浓度变化Fig.5 Changes in the concentration of OH-

图6所示为H+浓度随时间的变化情况。由于蚀孔处的沉淀不断增多，阻碍了Fe3+向孔外扩散以及OH-向孔内扩散，导致孔内大量Fe3+聚集，继而发生水解反应，产生大量的H+，初生蚀孔底部H+浓度变大，进一步腐蚀金属基体，金属加速溶解，产生次生孔，推动点蚀的稳定发展，蚀孔逐步向深处生长。

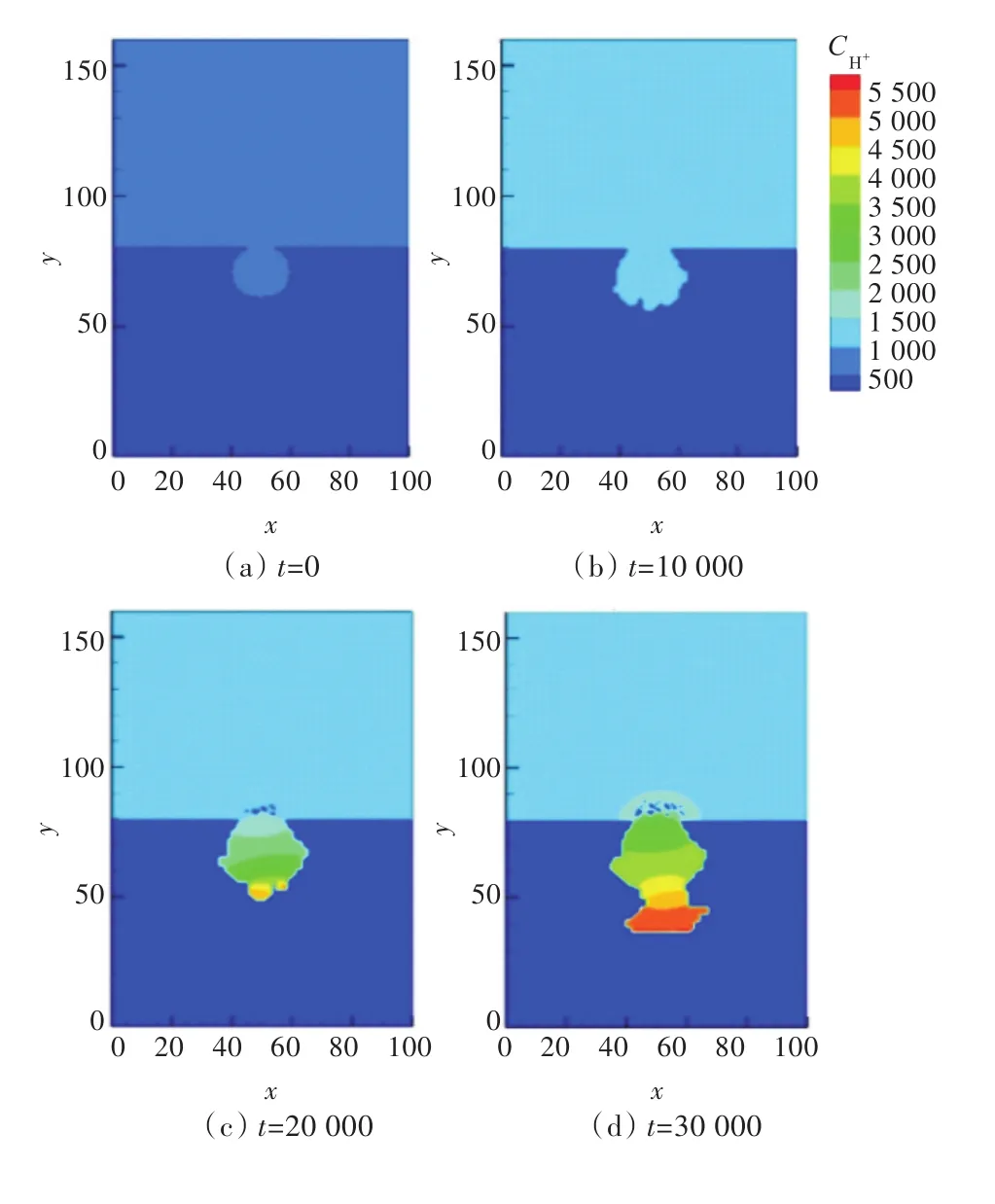
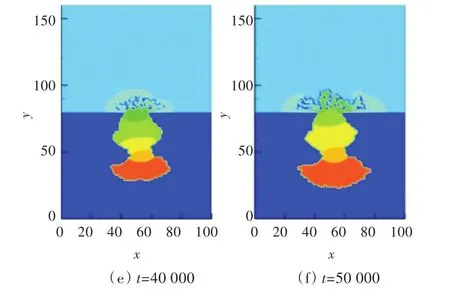
图6 H+浓度变化Fig.6 Changes in the concentration of H+

图7所示为整个腐蚀过程中被腐蚀的金属体积随时间的变化关系。当t=0～20 000时，金属腐蚀仅发生初生蚀孔的吸氧腐蚀，初生蚀孔被腐蚀的体积V逐渐变大，蚀孔的深度h逐渐增大；当t＞20 000时，由于孔内闭塞及酸化的腐蚀环境，导致金属自催化腐蚀反应的发生，腐蚀速率大于先前单独发生的吸氧腐蚀的速率，并且V随t的增加而增大，h也逐渐增大。

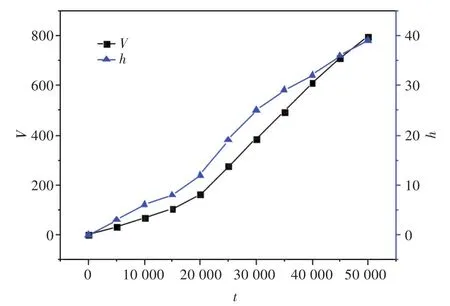
图7 腐蚀程度随时间的变化Fig.7 Variation of the degree of corrosion with respect to time

3.2 影响因素分析

3.2.1 腐蚀化学反应速率

模拟过程中，通过改变式（1）反应的化学反应速率，得到某一时刻（t=50 000）不同腐蚀化学反应速率下点蚀坑的形貌（图8）。从图中可以看出，在相同腐蚀时间下，随着腐蚀化学反应速率的降低，腐蚀程度减小。

通过对图8中V和h进行统计测量，得到t=50 000时V和h与k1的关系曲线（图9）。从图9可以看出，随着k1增加，V越大，h就越大。由于式（1）中化学反应速率的增加，导致了吸氧腐蚀加快，腐蚀产物增多，蚀孔内Fe3+浓度增大，加速了Fe3+水解过程，产生更多的H+，使孔内阳极金属进一步加速腐蚀，因此呈现出以上结果，并且该结果与真实情况相符。

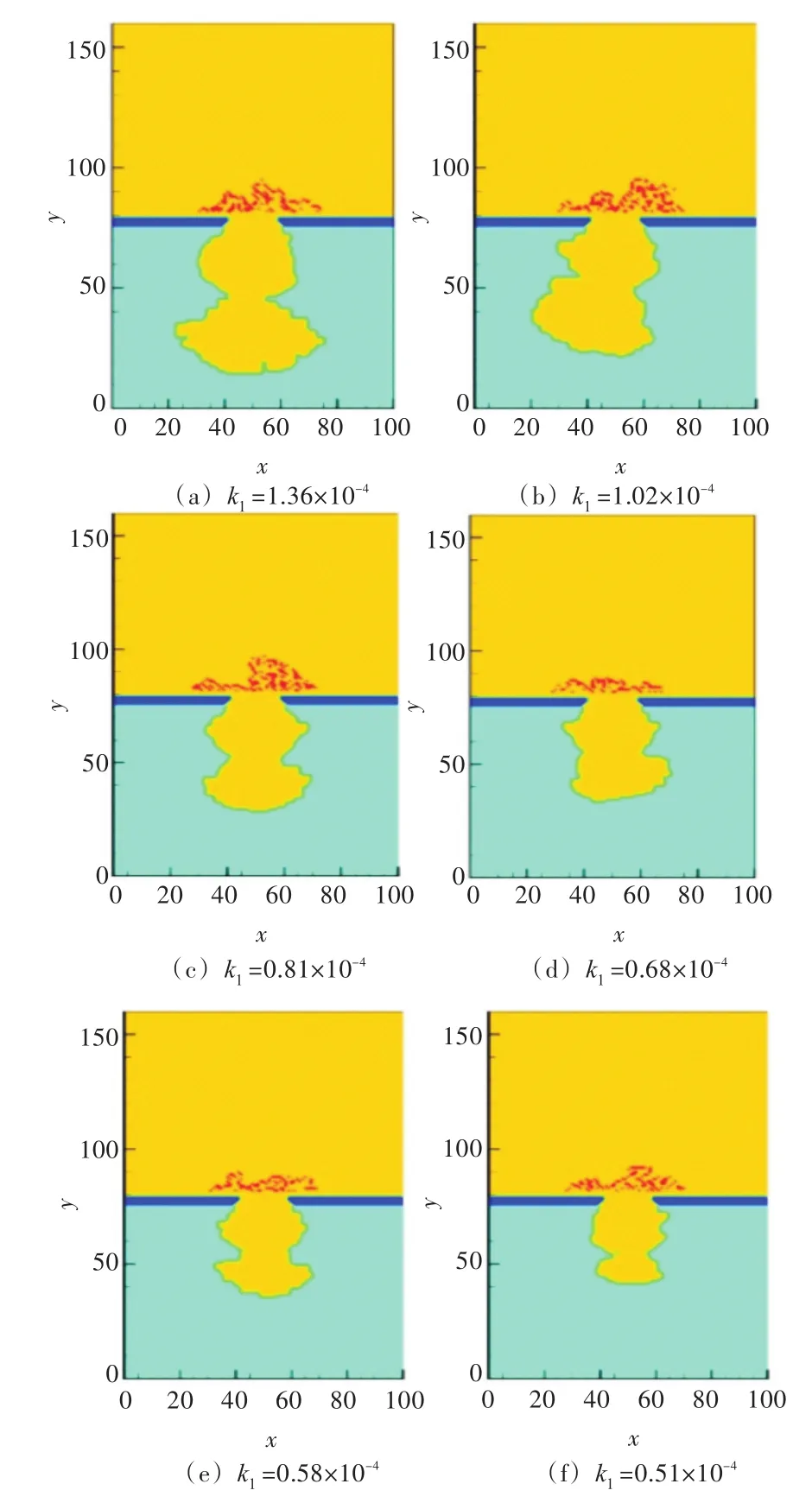
图8 不同腐蚀化学反应速率下的点蚀坑形貌Fig.8 The corrosion pit appearance of different chemical reaction rate

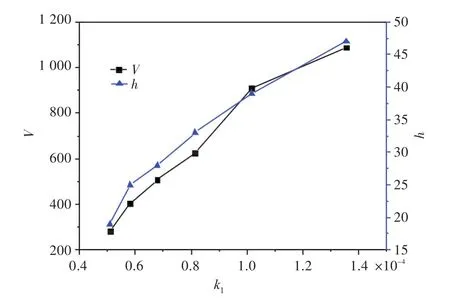
图9 腐蚀程度随腐蚀反应速率的变化Fig.9 The degree of corrosion varies with corrosion reaction rate

综合分析图8与图9可知，由于k1增加，单位时间内V变大，h增加。

3.2.2 腐蚀溶液扩散系数

通过改变模拟过程中浓度场含氧溶液的扩散系数，研究腐蚀反应中介质间流动与扩散对腐蚀的影响。图10给出了某一时刻（t=50 000），不同腐蚀溶液扩散系数下腐蚀坑的形貌。从图中可以看出，相同的腐蚀时间下，随着的增大，腐蚀程度加重。

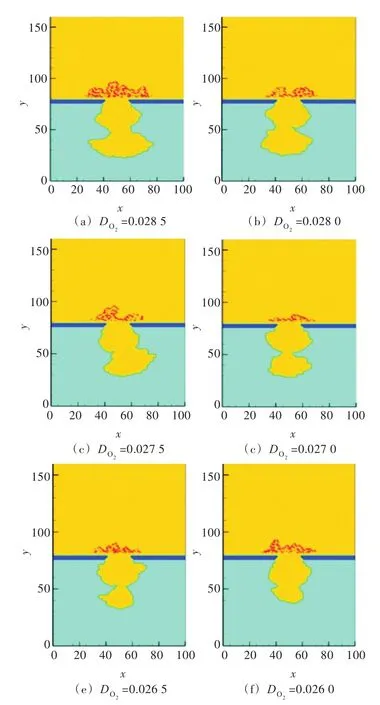
图10 不同腐蚀溶液扩散系数下的点蚀坑形貌Fig.10 The corrosion pit appearance of different solution diffusion coefficient

通过对图10中V和h进行统计测量，得到t=50 000时V和h与DO2的关系曲线（图11）。从图11可以看出，随着的增大，V越大，h越大。由于的增加，导致腐蚀溶液向蚀孔内扩散速率加快，金属腐蚀边界的浓度相对较高，加快了腐蚀反应，因此，呈现出以上模拟结果。

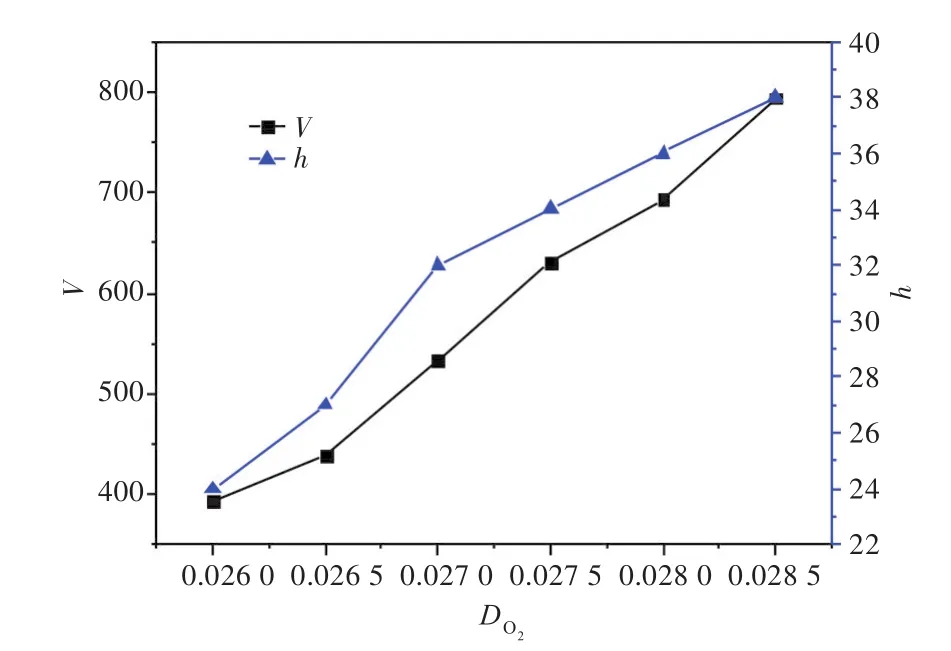
图11 腐蚀程度随O2扩散系数的变化Fig.11 Variation of the degree of corrosion with respect to diffusion coefficient of O2

3.2.3 腐蚀产物扩散系数

在模拟中改变浓度场的腐蚀产物Fe3+的扩散系数，研究腐蚀产物扩散系数对腐蚀程度的影响。图12所示为某一时刻（t=50 000）不同腐蚀产物Fe3+扩散系数下腐蚀孔的形貌特征。从图中可以看出，在相同的腐蚀时间下，随着的减小，腐蚀程度加重。

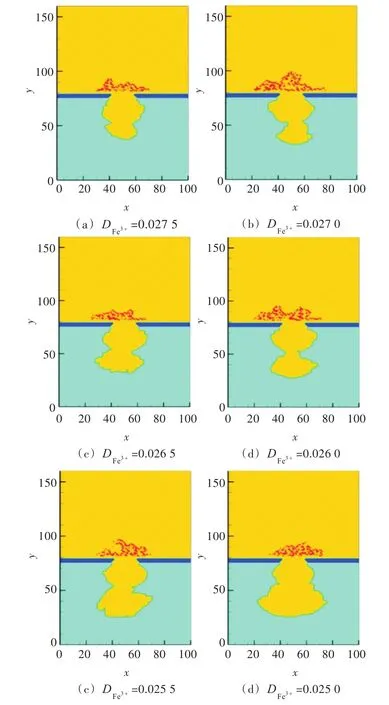
图12 不同腐蚀产物扩散系数下的腐蚀坑形貌Fig.12 The corrosion pit appearance of different corrosion products diffusion coefficient

通过对图12中V和h进行统计测量，得到t=50 000时V和h与的关系曲线（图13）。从图13可以看出，随着的降低，V越大，h越大。由于的降低，导致蚀孔内Fe3+的大量聚集，加速了Fe3+的水解过程，产生了更多的氢离子，使孔内的酸度增加，金属基体的腐蚀溶解速率增加。因此，呈现出以上模拟结果。

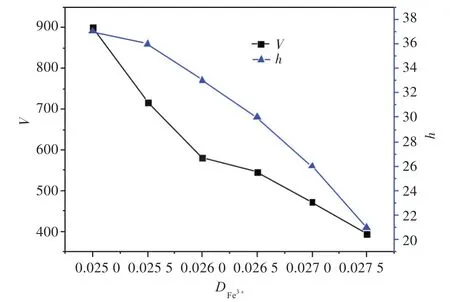
图13 腐蚀程度随Fe3+扩散系数的变化Fig.13 Variation of the degree of corrosion varies with respect to diffusion coefficient of Fe3+

4 结 论

本文基于改进后的LB腐蚀模型，将钝化概率函数引入VOP方法中，对腐蚀化学反应速率进行修正，建立了LB腐蚀模型。使用该模型，模拟了浸没于液体腐蚀环境中的金属表面单坑点蚀稳态过程，通过模拟得到以下结论：

1）LBM算法可以明确得到溶液中不同组分的流动与扩散，由此得到其浓度分布，通过流场和浓度场之间的耦合模拟真实的液体腐蚀环境；引入钝化概率函数使得模拟的腐蚀坑的形貌随机变化且不对称，更加符合真实的腐蚀坑形貌；阴、阳极共同作用使电化学腐蚀的模拟更加完善；VOP方法可以控制腐蚀的快慢，而不是简单的固、液相随机转换。

2）腐蚀反应速率越大，在相同的腐蚀时间下，在金属表面点蚀的稳态过程中，金属被腐蚀的体积越大，腐蚀的深度就越大；腐蚀含氧溶液扩散系数越大，在相同的腐蚀时间下，金属被腐蚀的体积越大，腐蚀的深度就越大；腐蚀产物Fe3+扩散系数越大，在相同的腐蚀时间内，金属被腐蚀的体积越小，腐蚀的深度就越小。