阻温系数：从能量传递到结构尺寸

王 信 伟

(爱荷华州立大学机械工程系， 美国爱荷华州 埃姆斯市 50014)

1 物理学背景：自由电子散射和温度的关系

图1中显示出了金属铱(Ir) 的电阻率(ρe)随温度(T)的变化，其中金属材料分别取Ir块体及镀在DNA纳米线表面的Ir薄膜[1]。尽管薄膜的电阻率比块体的电阻率大很多，前者是后者的5～6倍；但是，这些材料的电阻率随温度的变化曲线之间基本上是平行的，其差值是由于材料的缺陷所造成。下面，用Bloch-Gruneisen公式[1]来解释此现象：

(1)

式中：右边第一项ρe,0为材料的残余电阻率，其值是材料在温度为0 K时的一个外推值。

对于大多数的块体材料，由于其内里的缺陷较少，这个残余电阻率基本为0，如图1所示。如果材料的晶格结构没有大的变化，那么右边第二项是不随材料的缺陷发生变化的。这一项反映了声子对电子的散射和声子的浓度成正比。如果金属的晶格结构缺陷太多，导致德拜温度变小，那么第二项也会发生变化，通常会变小。这种现象，被称为声子软化(phonon softening)[1]。由此可以看出，图1中各个样品的电阻率差值是由于材料缺陷所引起。式(1)反映了温度对于电子散射的影响。

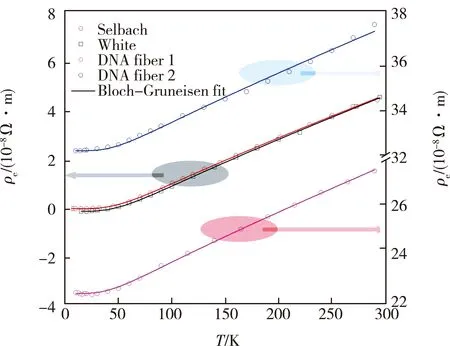
图1 块体Ir及纳米线表面Ir薄膜电阻率随温度的变化[1]

对于电阻率的解释，还可用式(2)来表示：

le=mvF(ne2)·l-1

(2)

式中：vF为费米速度；m为电子的质量；n为自由电子的浓度；l为电子的平均自由程。

根据Matthiessen 定律,有：

(3)

式中l0和lp分别为结构缺陷和声子散射引起的电子的平均自由程。图1所显示的结果也直接验证了Matthiessen定律。

供应链金融风险可以看作是由宏观或微观的经济因素决定的，也有可能是单纯因为道德风险造成的，是一种功利主义的恶性发展。想要规避道德舆论导致的金融风险，首先需要从金融活动的当事人出发，对其自身情况包括收支数据等进行把控，并在追求利益的同时，对其进行起码的道德约束和法律约束。道德舆论可以看作是一个历史范畴，一定的金融市场决定了其势必出现相应的社会道德。同一个社会中，不同的人又具有不同的道德去向，尤其是在大数据网络环境下，金融市场的监管力度会随之削弱，这就要求有关单位和当事人必须学会妥善利用网络金融道德舆论和法律武器，进行风险规避。

声子对电子散射引起的平均自由程与声子结构有关系。温度引起的电阻率变化纯粹是由于声子结构的影响，主要来自声子浓度随温度发生变化的影响。这是因为，电子浓度不随温度变化而变化。这里的残余电阻率可以用来计算材料缺陷所引起的电子平均自由程。这个平均自由程通常和金属的晶粒尺寸极其相近，所以我们称其为材料的结构尺寸。

2 电子的阻温系数

上述内容中，描述了电阻率和材料结构及其缺陷的相互关系。那么，对于热传导问题，我们是否可以定义一个热阻率，用于研究和表征材料缺陷对导热性能的影响？电阻率是材料导电率的倒数，那么我们能否用导热系数的倒数来定义热阻率，直接观察材料缺陷对导热性能的影响？答案是否定的。

这是因为，导热系数或热阻率中包含了材料热容的影响。这可以从简化的能量载流子(声子或电子)单一散射时间的公式中看出。在单一散射时间的框架下，导热系数可以写成式(4)：

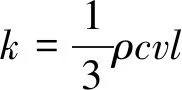
(4)

热阻率表示成：

ρT=1k=3(ρcvl)

(5)

式中：热容c是随温度发生变化的；载流子的平均自由程l也随温度发生变化。

这两种现象纠缠在一起，就形成我们经常看到的导热系数随温度发生变化的峰值(见图2)[2]。 峰左边导热系数随温度的变化主要是热容的影响所致，其右边是缺陷-声子及声子-声子散射共同影响所致，其中也有热容随温度发生变化的影响。在过去研究材料导热系数的文献中，通常是通过导热系数随温度的变化来研究材料缺陷对传热的影响。

现在，我们定义一个新的参数，以去除热容随温度变化的影响。这个参数称作阻温系数(Θ)，定义为Θ=ck。该参数的概念可以解释为，单位热容的能量载流子的热阻率；其定义式中的c是指能量载流子的热容，在很多时候它并不是材料的宏观热容。在金属中，自由电子是传导热量的主体(>90%)，那么这里就要用到自由电子的热容。自由电子的热容反映了自由电子在费米面附近的能级占有情况。自由电子的热容可以表达为c=γT，其中γ是常数，所以，金属的阻温系数定义可以表达为Θ=γTk。

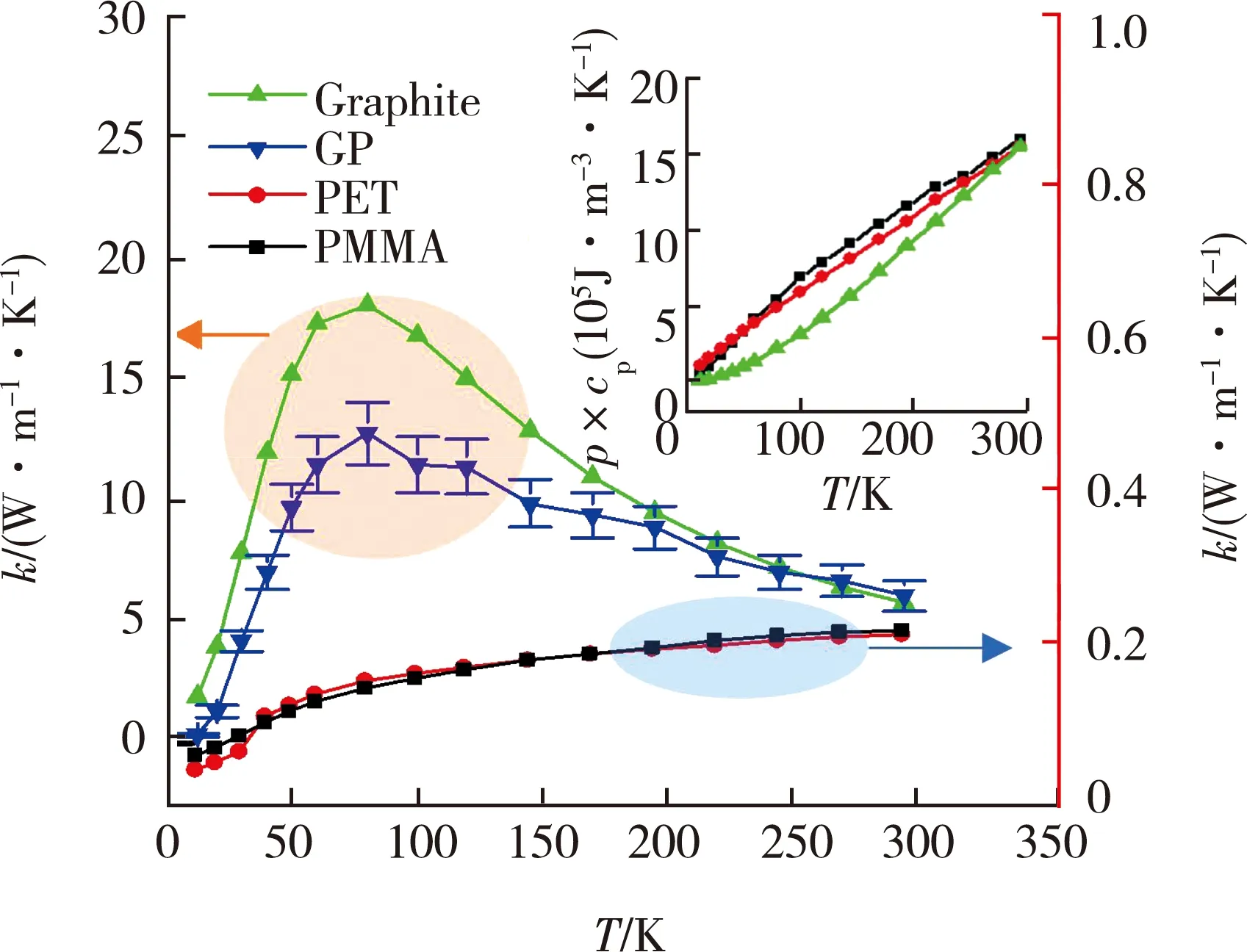
图 2 石墨烯纸和石墨的c-向导热系数随温度的变化[2]

阻温系数的提出，并不仅仅是针对数学公式的变换，它更有助于我们揭示一些隐藏的物理规律。我们研究了银纳米线(直径为227 nm)导热系数随温度的变化规律(见图3)[3]，并在图3中画出了块体银导热系数随温度的变化以作对比。从中可以看出，纳米银线的导热系数随温度的变化趋势和块体银完全相反，并且它们的量级也不一样。从中完全看不出，此纳米材料和宏观材料的结构有什么区别和联系，以及这个结构区别和联系如何影响导热系数。

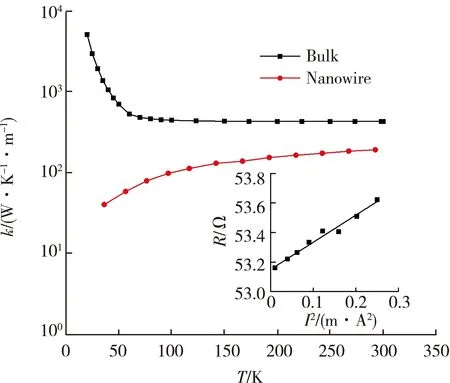
图3 银纳米线导热系数随温度的变化[3]

图4中，显示了阻温系数随温度的变化[3]。因为γ是常数，我们就直接用导热系数的倒数乘以温度。当时我们把这个参数称作Unified thermal resistivity, 实际就是现在讨论的阻温系数。 从图中可以非常清楚地看到，2条曲线是平行的，其差值是由于纳米线中的结构尺寸缺陷对电子的散射所引起。这也直接验证了Matthiessen定律在电子传热中的正确性。这是第一次观测到，金属中电子传热在纳米量级和宏观尺寸的平行与直接相关性。此观测结果，直接验证了Matthiessen定律。

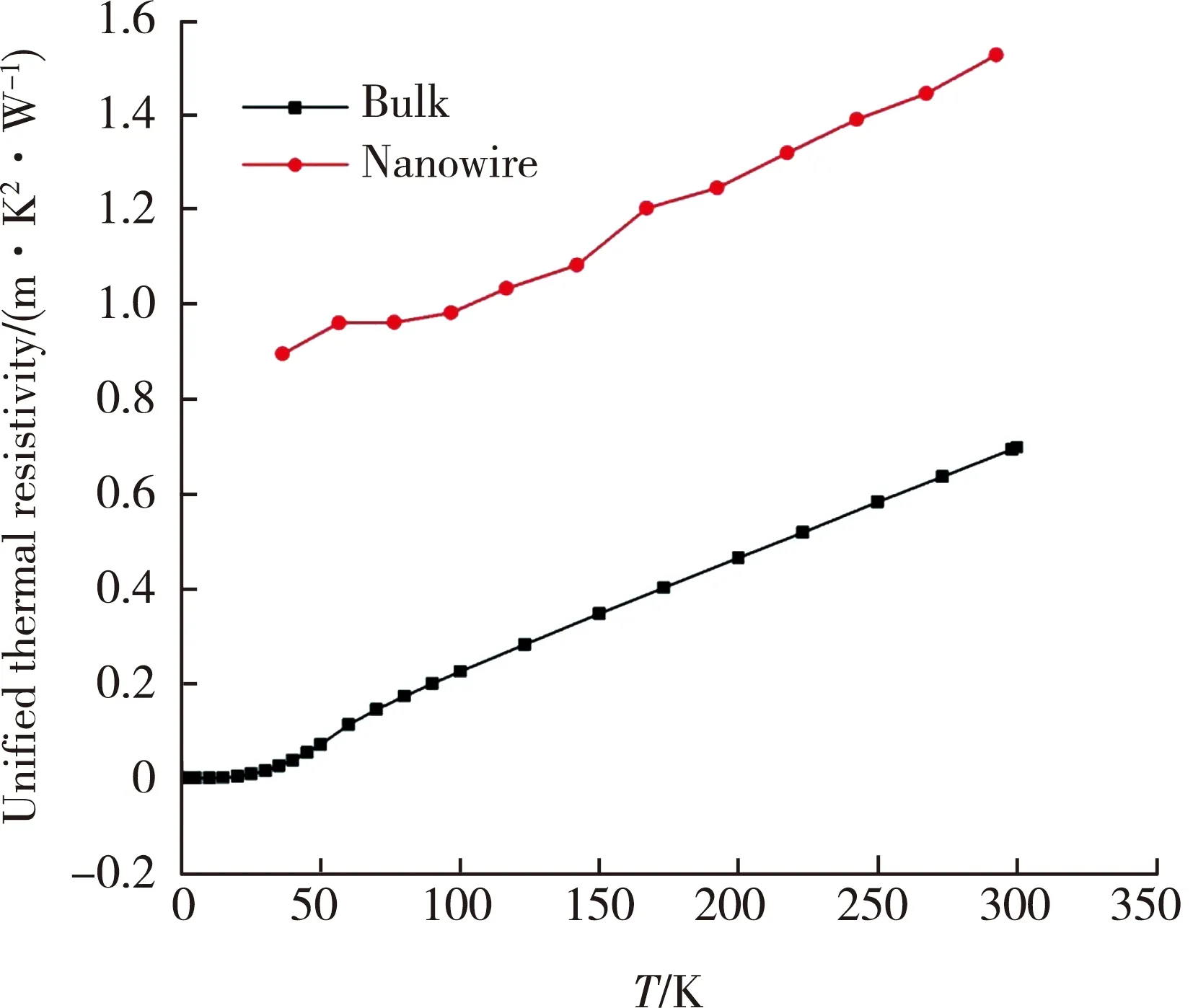
图4 块体和银纳米线的阻温系数随温度的变化[3]

那么是否存在纳米材料阻温系数随温度的变化和宏观材料不平行的情况呢？答案是肯定的。当晶格结构发生较大变化时，这种情况就会出现。这个特性稍后介绍。

3 声子的阻温系数

如果非金属材料不是各向异性，那么其阻温系数可定义为：Θ=ρck。这正是材料的热扩散系数(α, 又叫导温系数)的倒数。在声子单一散射时间的框架下继续展开，可以得到：

Θ=3(vl)=Θ0+Θp

(6)

Θp是由材料的声子结构和密度所决定，可写为式(7)[4]：

Θp=3(vlp)=c1exp(-BT)

(7)

B是和材料的德拜温度(TD)成正比的一个参数，可写为B=TDb，其系数b为2～3，具体取值和声子在波向量空间的分布有关。Θ0是材料的残余阻温系数，可以写为Θ0=3(vl0)。 其中，l0是材料的缺陷散射引起的声子的平均自由程，通常与材料的晶粒尺寸极其相似。

图5中给出了石墨烯海绵及石墨相关系数随温度的变化情况[4]。通过公式(7)可以确定德拜温度是1 813 K，非常接近文献中石墨烯的3个德拜温度(声学声子的3个振动模式)的平均值 —— 1 911 K[4]。图5显示，石墨的残余阻温系数非常小，接近0， 和图1中宏观材料的残余电阻率很相似。同时，声子阻温系数随温度的变化趋势也和电阻率随温度的变化趋势极其相似，反映了声子浓度随温度的变化。这也再次证明，阻温系数是与电阻率对等的物理量。这里直接证明了声子和电子在传热能力随温度的变化方面，具有极其相似的变化规律。通过大量数据分析验证，对于结构缺陷极其缺乏的宏观材料，它的阻温系数在温度趋近于0 K的时候，确实是趋近于0[1]。同时图5也表明，材料的德拜温度可以通过传热直接确定。这在传热学史上也是第一次。这表明，传热不仅有极其重要的工程应用背景，在材料的微观结构表征方面也得到了基础性的应用。

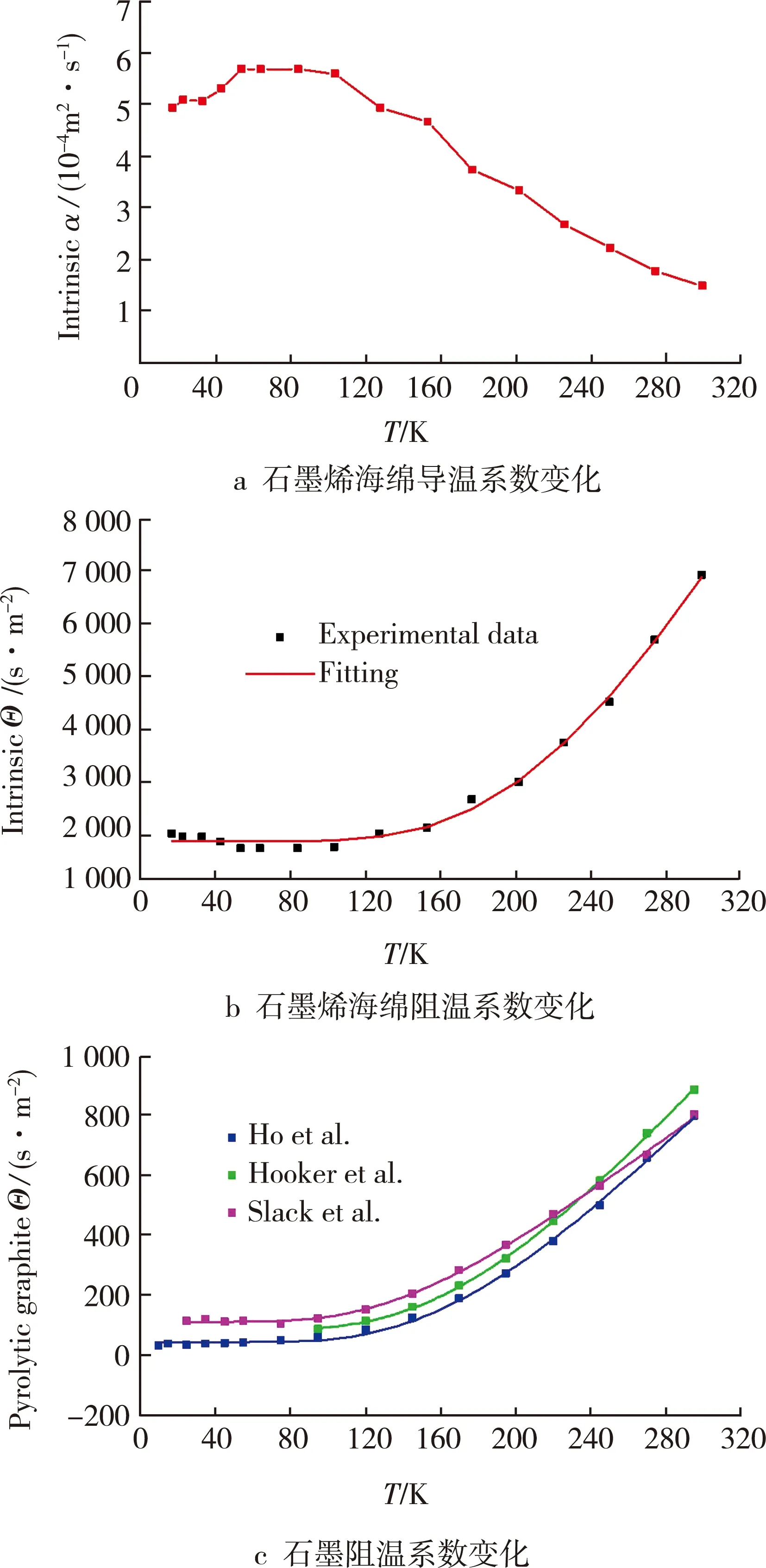
图5 石墨烯海绵及石墨相关系数随温度的变化[4]

在此，声子在0 K条件下外推的残余阻温系数所确定的声子平均自由程，反映了极低频率、极低动量的声子散射过程。这种声子的波长非常长，远远大于点缺陷的尺寸，因此，主要受晶粒界面的影响，它能非常准确地反映晶粒的特征尺寸。针对人的头发，用阻温系数的物理概念算得晶粒尺寸是1.6 nm，而通过X射线散射测得晶格尺寸是1.8 nm[5]，二者极其接近。我们测得DNA中的结构尺寸是0.64 nm，正是2个碱基对的长度[1]。对于很多非晶材料，一般的射线散射方法无法获得散射峰和结构尺寸，但是此时用阻温系数的残余值仍然可以测得材料的纳米量级的结构尺寸。对于二维材料，由于它们的厚度极小(纳米级)， 应用X 射线散射无法获得面里结构的散射峰，更无从获得面里的材料结构尺寸。但是我们可以通过观测二维材料面方向上阻温系数随温度的变化，获得0 K下的残余阻温系数，从而获知材料的结构尺寸。此相关工作正在进行中。这项工作极大地扩展了传热的研究范围，提供了一种从低动量声子散射测量材料晶粒尺寸的方法。

由上述内容可知，阻温系数是导温系数的倒数。导温系数(热扩散系数)是可以直接测量的物理量，可以用我们实验室发展起来的TET法[6]、激光闪光法[7]及PLTR等方法进行测量[2, 8]，且能够达到非常高的测量精度。我们应用TET法测量，只需要将材料加热1 ℃左右即可，甚至加热更低(<0.1 ℃)也可。这极大地推进了阻温系数的测量及其残余值的确定。

4 各向异性的声子热容和阻温系数

前面提到对于阻温系数的定义，必须用能量载流子本身的热容。在此，以石墨烯纸为例予以说明。此材料是由石墨烯一层层叠加而成，是强各向异性材料。在面方向上，导热系数可写成k=12cavala；在厚度方向上，导热系数可写成k=c1v1l1。这里的ca和c1截然不同：ca是速度沿面里的声子的热容；c1是速度沿厚度方向的声子的热容，只占石墨烯总热容的很少的份额，在室温下，约占 5.8%[2]。此热容实际上是石墨烯层与层之间原子相互作用(范德华力)下的热容。这种各向异性的热容概念，区分了原子在不同方向上相互作用所需能量的分配。对于石墨烯材料，其厚度方向上原子之间的相互作用为范德华力，很弱，所以，这个方向上分配的热容很小。图6中，显示了石墨烯纸总热容和厚度方向(c1)热容随温度的变化[2]。可以看出，当温度降低时，厚度方向的热容占比开始增大[2]。具体各向异性热容的计算可以参考我们对于石墨烯纸的详细研究[2]。

图7中，显示出了石墨烯纸c-向的(c-axis)阻温系数随温度的变化[2]。在室温下，根据这种各向异性的热容概念，我们得到了当材料无缺陷时其厚度方向的声子的平均自由程：138 nm。这就准确地解释了以前大家在分子动力学模拟和实验中观察到的厚度方向的声子平均自由程：146 nm。通过残余阻温系数，我们得知厚度方向的结构尺寸是234 nm。这种大尺度的结构尺寸用X射线散射极难测量。这是因为，结构尺寸引起的峰宽太小，小于系统的测量极限。

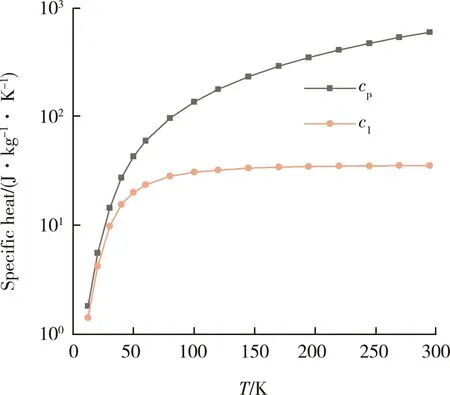
图6 石墨烯纸总热容(cp)和厚度方向热容(c1) 随温度的变化[2]

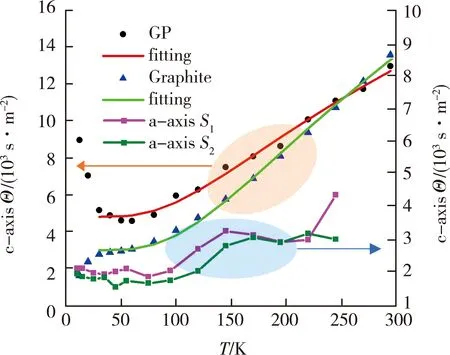
图7 石墨烯纸c-向阻温系数随温度的变化与石墨的比较[2]

5 从阻温系数揭示结构变化

以上内容中，主要介绍了残余阻温系数及其缺陷在阻温系数中的影响。还有一点非常重要： 阻温系数随温度的变化趋势。如果材料的物理结构不随温度发生变化，那么阻温系数随温度的下降呈下降趋势，并且趋于一个常数：残余阻温系数。但对于有的材料，如果内部物理结构不稳定，随着温度的下降会发生恶化，那么阻温系数会随着温度的下降而升高， 如图8所示[6，9]。图8中，显示了石墨烯气凝胶(GA)和半还原石墨烯纸(PRGP)的阻温系数随温降的变化[9]。它们表现出了和一般材料截然不同的趋势。这种材料结构的变化，不容易从导热系数随温度的变化当中发现，但是可以从阻温系数随温度的变化中很清晰地观测到。这再次表明，相较于导热系数，阻温系数可以更直接地反映材料结构对传热的影响，使得其物理规律与现象的研究更加深刻和广泛。

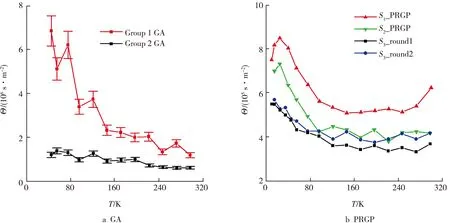
图8 石墨烯气凝胶(GA)和半还原石墨烯纸(PRGP)阻温系数随温度的变化[6，9]

6 结 语

应用阻温系数直接观测和研究材料缺陷对导热性能的影响，其作用比研究导热系数随温度的变化更直接、更有效、更广泛。阻温系数是对等于电子电阻率的一个导热物理量，用它也可直接计算材料的有效德拜温度。阻温系数的残余值反映了低动量声子或电子所受的晶粒散射。对于多晶材料，可以用来得到一个和X射线散射对等的，甚至极其相近的结构尺寸[10-13]；对于非晶体材料，可以获得运用一般射线散射方法无法得到的纳米或原子量级的结构尺寸。各向异性材料热容的概念，可以用于各向异性的阻温系数和结构尺寸的计算。阻温系数随温度的变化规律，可以直接用于研究材料的结构随温度变化的稳定性。上述分析也可以通过研究能量载流子的平均自由程的倒数而获得，不过阻温系数通常通过实验就能够直接测量，无需再额外处理。

致谢：在阻温系数的研究过程中，得到了来自美国自然科学基金会的支持(CBET1235852， CMMI1200397， CMMI1264399，CBET1930866)。在此深表感谢！

声明：本文中采用的图片和数据均已得到出版商的正式许可。