露天矿山开拓运输系统道路选线算法

刘光伟，柴森霖,3，白润才，赵景昌，李浩然，张 靖

(1.辽宁工程技术大学 矿业学院，辽宁 阜新 123000; 2.辽宁工程技术大学 辽宁省高等学校矿产资源开发利用技术及装备研究院,辽宁 阜新 123000; 3.盐城工学院 经济管理学院，江苏 盐城 224051)

露天矿山线路工程是矿山开拓运输系统建设的重点工程之一，是建立采场、排土场以及地面辅助设施运输联系的重要保障，同时也是直接影响剥离物运输效率、运输成本的关键因素，对于露天矿山降低生产运营成本具有十分现实的经济意义[1-3]。

目前，关于露天矿山开拓运输道路选线问题的研究仍十分有限，现有的研究成果多以露天矿设计规范[4-5]中给出的开拓定线原则为基础，采用人工经验试错的方法制定选线方案，最终采用典型方案对比确定最优化线路，如余鼎等[6]根据山坡露天矿的地理、地形条件，提出一种适合山区特殊地质概况的道路选线方法。这种依赖主观经验的手工定线方法，其优点在于全程均包含主观设计，适应性强，方案设计相对更灵活，但也存在极为明显的局限性，如人工试错工程量大、精度低、主观经验错误易造成全局性的错误决策。近年来，随着数据采集手段的发展，孙效玉等[7]针对既有线路提取过程中存在路段缺失、线路偏移等问题，修正了传统路网采样过程中存在GPS数据偏移严重、路网连通性差等问题，并结合滤波方法和栅格图像细化算法，提出重新构建道路运输网络骨架，实现采样线路的矢量化重构的新方法，在一定程度上改善了现有运输系统优化的基础运输网络建设问题。其实，对于前述的这类道路选线问题的研究在高速公路施工选线应用中更为广泛，如JYH-CHERNG和JONG等[8]基于连续剖面法和遗传算法提出高速公路选线算法;JHA M K等[9]结合城际高速公路选线问题，提出智能选线计算框架。这类算法的优势在于自动化程度高、以费用为优化目标、主观经验性干预小、能显著减轻选线的任务量，极大限度地优化道路设计、施工及使用成本。但这类方法在实际矿山应用中也存在一定的局限性，如算法迭代过程中易陷入局部最优、基于随机特性的寻优策略计算效率低、JONG提出的选线理论会自动舍弃矿山中的折返路径解等。

笔者在综合上述研究成果的基础上，针对城际高速公路选线方法直接应用于矿山道路选线问题时存在的局限性，提出一种考虑折返路径解的分阶段选线剖面布置方法，并结合三维路径桩点的几何特性分析、曲线线形约束检测等方法，构建了一种适用于求解露天矿山选线问题的高效算法;为进一步提高算法的求解效率，笔者对遗传算法进行了改进，并将生物激励神经网络全局激励、抑制本地驻留的特性引入遗传算法的基因编码过程中，来实现启发式路径修正。本文以神华新疆准东露天煤矿为研究实例，进行算法仿真实验，经应用实例验证，改进后的算法实用可靠，能满足矿山高效、最优化开拓运输系统定线的工程需求。

1 选线基础理论

1.1 分阶段的选线剖面布置方法

露天矿山开拓运输系统定线本质上与公路选线相同，其目标都是在三维空间中选出一条符合运输条件且在寿命周期内总成本最低的道路中心线，以建立源节点和目标节点间的有效运输联系。目前，主流的三维道路选线算法多基于JONG等[8-9]提出的连续剖面选线理论，其原理如图1所示，即在源节点和目的节点间建立多组连续剖面，通过随机初始化剖面上的控制点并连线，建立备选道路中心线方案，最终结合群智能算法和费用目标函数进行路径的优选。

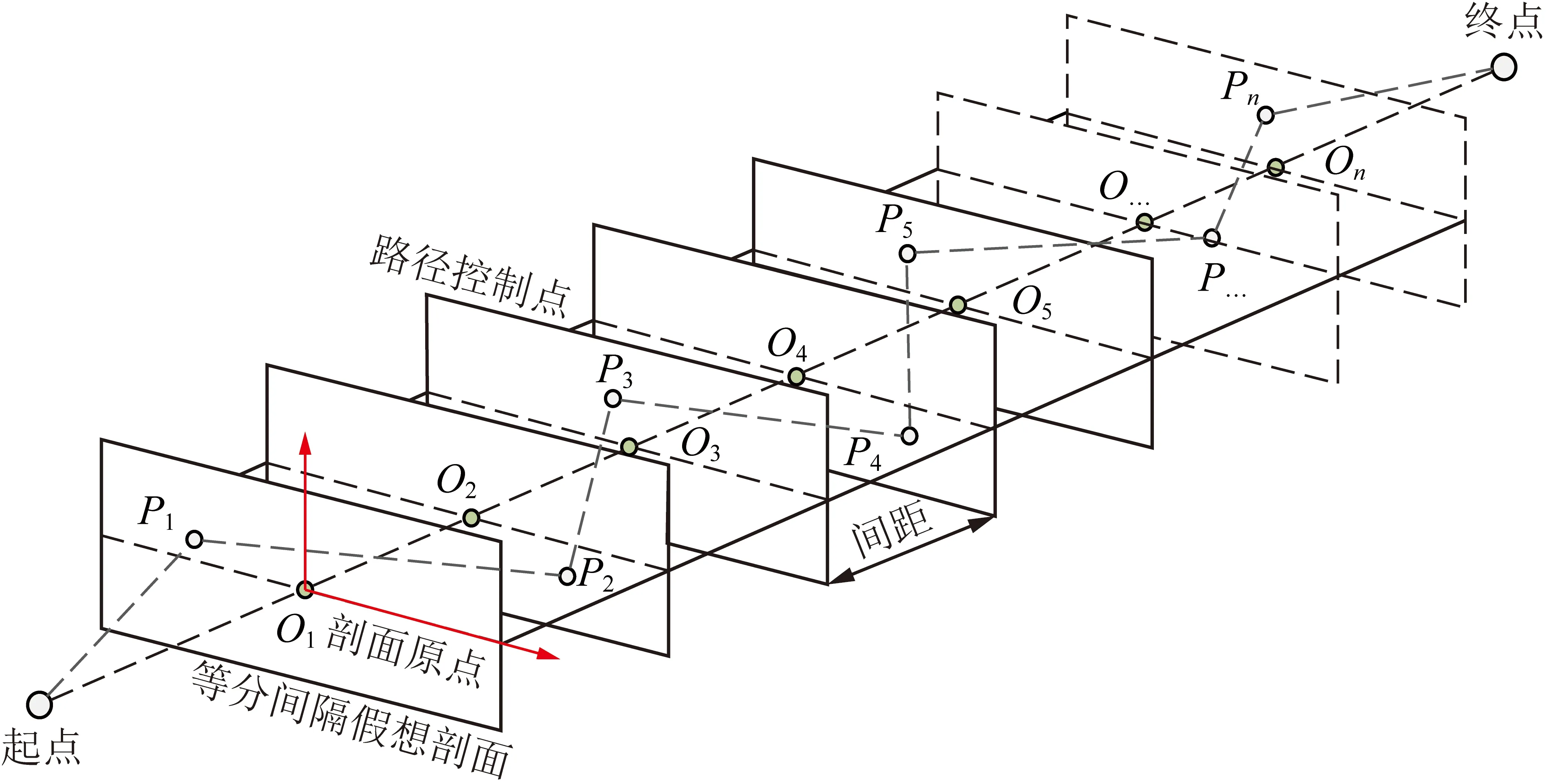
图1 连续剖面选线算法原理Fig.1 Schematic diagram of continuous profile route selection algorithm

相比于传统的手工定线方法，JONG提出的选线算法有效提高了选线的效率和精度，但在露天矿山开拓定线的实际应用中却存在明显的局限性，这主要表现在此种方法要求路径的矢量方向应始终一致，即路径与剖面间有且仅有唯一交点，如图2(a)所示，这也限制了备选线路径解中不应包含折返路段。但对于露天矿山运输道路选线问题，特别是当采场内的开拓运输线路存在移动坑线时，被布置于工作帮的多条运输线路极可能存在折返现象，如图2(b)所示，这将导致直接应用JONG法选线将存在明显的局限性。

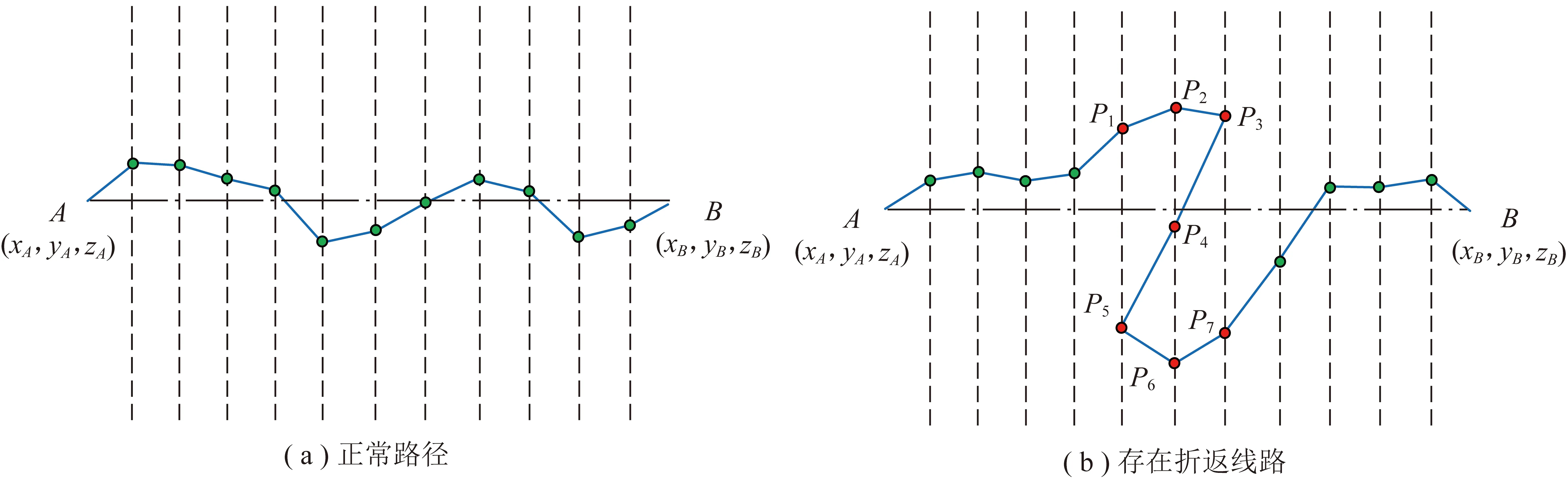
图2 JONG选线算法的剖面布置形式Fig.2 Profile layout of JONG’s route selection algorithm

为使JONG论证的剖面交点唯一的条件假设对于所有的路径备选解均成立，文中对JONG算法中的剖面布置形式进行了改进，提出一种分阶段的剖面布置形式，具体布置方法如下:

步骤1:首先根据采场内的开采参数，沿台阶垂线方向计算线路的极限投影δ，并按照阶段宽度恒大于极限投影δ设置选线剖面，如图3所示，即保证阶段宽度能包住整个折返路段;

步骤2:按照第1阶段剖面布置设计路径骨架桩点。对于如图2所示的线路形态，其骨架桩点即可布置为如图3所示的X1～X6蓝色多段线节点所示的形式;

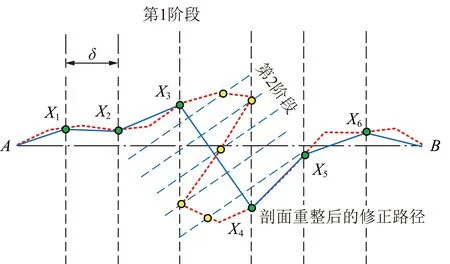
图3 分阶段选线剖面布置形式Fig.3 Stage route selection profile layout

步骤3:选取第1阶段路径骨架线中相邻节点，分别构建第2阶段选线剖面，如图3所示的X3～X4区间内的虚线所示;

步骤4:在第2阶段选线剖面上初始化路径桩点，如图3中黄色桩点所示，即可在满足假设条件下逼近所有路径解。

1.2 分阶段三维路径节点代数化表达

上述选线剖面的布置方式描述了线路桩点的几何形态组成，但却无法对各桩点具体的几何位置进行有效表达。因此，为实现对线路中几何约束的代数化运算，以各剖面为单位构造独立的坐标系统，并利用坐标系统中心点间的位置关系来建立各桩点之间的位置联系。其计算步骤如下:假设图1中线路已知起点、终点分别为A(xA,yA,zA),B(xB,yB,zB)，各干线剖面的直角坐标系原点为Oi(xB,yB,zB)，两者之间联系可以采用单位向量的方式来表达，故源节点和目的节点间的单位向量可表示为

(1)

故按照式(1)中所示的单位向量，各坐标系之间的关系可表示为

(2)

则每个干线桩点在各自坐标系中的位置坐标可表示为

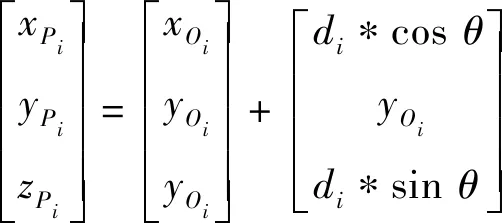
(3)

式中，di为Pi至Oi的欧式距离;θ为向量OiPi与X轴正方向的夹角，θ∈[0,π]。

考虑剖面存在两个阶段的嵌套布置，故在剖面阶段内仍可采用与式(1)～(3)相类似的坐标嵌套，故可推导出分阶段的剖面内部的桩点位置坐标，其阶段内单位向量可表示为

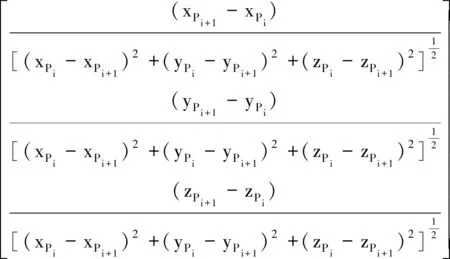
(4)

阶段内嵌套后的坐标系关系则可表示为

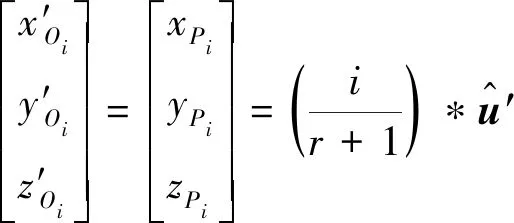
(5)

全路径的桩点坐标则可以表示为

(6)

式中，d′i为节点P′i与O′i的欧式距离;γ为在以O′i为原点的坐标系下，向量O′iP′i与X轴正方向的夹角，γ∈[0,π]。

1.3 曲线设计与约束检验

由上述桩点序列坐标连接而成的备选路径中心线,其实质上均为存在曲率突变的参考路径解。但是，按照此种方式构造出的备选路径解是存在行车安全隐患的。通常，为消除这种曲率突变隐患，使道路行车安全、平顺，手工选线方法会在主观选定中心线的局部位置进行元素设计，以保证各区间路径满足相应的道路规范要求。因此，为保证算法虚拟出的路径能满足后期主观线形修正的要求，笔者按照《厂矿道路规范》[4]中给出的道路线形指标(具体参数见表1)，利用相邻桩点属性建立每一个几何特性突变点的检验判据，从而为后续算法对路径的判别检验提供基础。

1.3.1平曲线约束检验

平曲线设计的首要任务是在满足安全视距条件下，进行合理的转弯半径设计，最大限度地提高转弯路段的行车安全性[4-5]。通常，在手工定线过程中，此部分设计需要在满足最小曲线半径的前提下，寻求安全性和运输经济性间的一个有效折中，即设计的半径过小，运距短有利于运输经济性，但视距短、清障工程量大、存在安全隐患、行车速度受限、需外侧设置超高;而转弯半径设计过大，则运距长、不利于运输经济性，但视野开阔、行车速度快、有利于行车安全及道路平顺性。由于优化选线算法可将运输经济性转换为对应的优化问题，因此该部分只关注线形约束，并考虑平曲线的曲线半径，可通过曲线上任意3点来计算，本文采用相邻桩点坐标建立最小转弯半径判据:

表1 曲线设计参数
Table 1 Curve design parameters

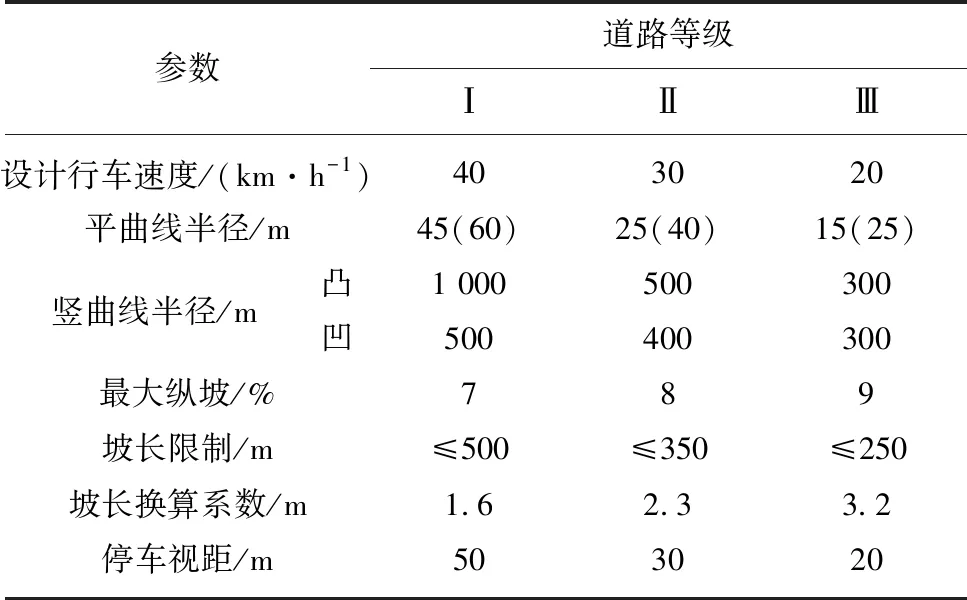
参数道路等级ⅠⅡⅢ设计行车速度/(km·h-1)403020平曲线半径/m45(60)25(40)15(25)竖曲线半径/m凸1 000500300凹500400300最大纵坡/%789坡长限制/m≤500≤350≤250坡长换算系数/m1.62.33.2停车视距/m503020

(7)

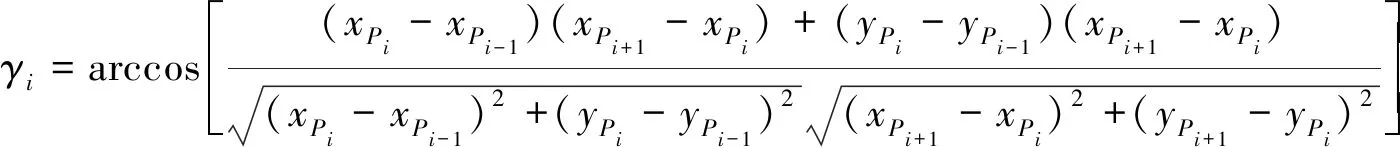
(8)

式中，Rmin为平曲线的最小曲线半径;Ri为任意3点计算的平曲线曲线半径。

1.3.2竖曲线约束检验

矿山卡车运输线路设计的另一个关键环节为竖曲线设计，这主要是因为重型卡车在纵坡下行时，极易造成事故及车辆故障，竖曲线设计的质量直接影响着行车安全性及运输平顺性。因此，为避免线路中存在极限纵坡及频繁连续下坡，竖曲线设计应满足两方面的约束限制:

(1)最大纵向坡度限制。为保证备选路径在相邻桩点间能够满足最大纵向坡度要求，对相邻路段的最大纵向坡度做如下限制:

gmax≥gi=|zi+1-zi|/dg(i)

(9)

式中，gmax为最大纵向坡度;dg(i)为坡度计算出的坡面间隔距离;zi+1-zi为相邻两线路节点的高程值。

(2)缓坡段的长度限制。为确保设计的线路能够满足充足视距以及运输平顺性的要求，避免车辆因纵向爬坡或下坡，而导致制动系统安全隐患及零部件损耗对缓坡段极限长度进行了约束，其长度约束如式(10)～(11)所示。

缓坡段长度上限:

(10)

缓坡段长度下限:

(11)

式中，L为竖曲线长度;S为停车距离;A为坡度差值;h1为视线高度;h2为障碍物平均高度。

1.4 线路费用成本模型

对于矿山道路的费用成本分析是指对在经济有效期内发生的所有与道路相关的全部资源代价投入的经济分析折算[4-5,10]，主要成本费用包括道路的建设费用和使用费用两部分。基于上述考虑，笔者将成本费用分为如下3种类型，并结合索引栅格技术，将模型中的位置信息、单元费用成本等属性进行关联，建立费用栅格地图，从而实现算法对给定线路费用成本的有效表达和快速索引。

(1)筑路费用成本(KP):主要包括凿岩爆破费用Kp、土岩结构稳定性维护折算费用Ks、构筑物移设折算费用Kd。

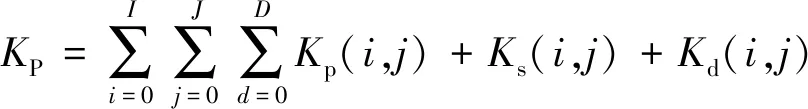
(12)

(2)道路使用成本费用(Ku):主要包括因道路使用而产生的道路构筑、变更、路面管理、设备维护和管理等费用以及因特殊交通状况而引起的附加费用。

Ku=ktLn+G(ρ)

(13)

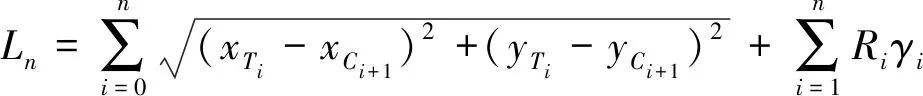
(14)

式中，kt为卡车的寿命周期内单位公里费用折算;ρ为车流密度;G(ρ)为关于车流密度对运输系统管理、调度和经济效益影响的非线性表达，取正为抑制生产效益，反之增强;Ti，Ci+1为曲线相邻切点。

(3)土石方量工程费用(Kv):包括因填、挖方而产生的工程费用和运输费用。

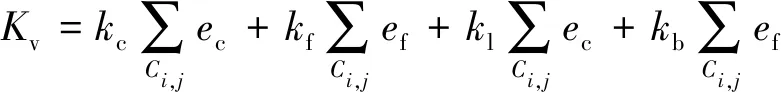
(15)

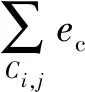
综上所述，选线道路的生命周期内总体费用成本可表示为

C=KP+Ku+Kv

(16)

2 基于IGA模型的开拓定线算法设计

2.1 改进遗传算法(IGA)设计

采用改进遗传算法[11-12]用于道路选线设计，本质上是一类在技术可行的道路布设方案中逼近预期费用目标最优化的数学规划问题，该规划问题建立在选线方案的费用成本最小目标之上，故其优化问题的目标函数可定义为

minC=Kp+Ku+Kv

(17)

在确立优化目标后，遗传算法将模拟“优胜劣汰”的生物进化模式，在问题潜在可行解中逼近现实路径最优解。为描述潜在可行解在寻优场景中适应性，采用式(18)作为基因个体的适应度评估函数，以保证生物选择能按照优化目标方向择优选择。

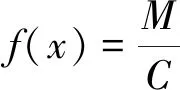
(18)

式中，M为适应度函数的镇定系数，其作用是防止当C极大时f(x)趋近于0而导致算法无法决策。

种群初始化主要通过在剖面位置随机选点以建立空间节点与基因编码之间的坐标映射，其中各路径的基因编码形式为

Γ=[γ1,γ2,γ3,…,γ3n-2,γ3n-1,γ3n]=

[x1,y1,z1,…,xn,yn,zn]

(19)

在上述种群初始化时，可行域内解的规模有限且缺乏节点位置的曲线设计，为进一步增强种群多样性、实现隐患节点的判别，文中对遗传算法进行了改进，主要包括3个方面:① 采用随机交叉和变异的方式以增强种群的多样性;② 采用基因位和基因段的变异以增强优秀个体多样性，避免陷入“过早熟”现象;③ 采用精英选择结合轮盘赌的方式，实现优秀种群个体的快速筛选。改进算法的设计流程如图4所示。

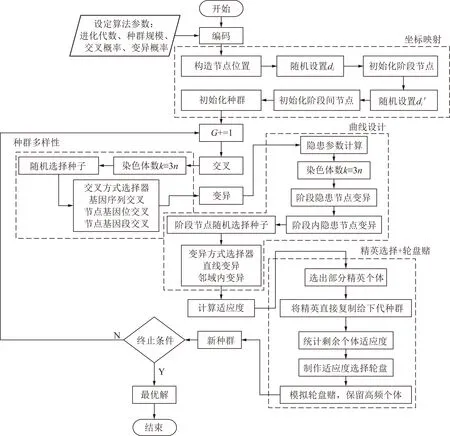
图4 IGA算法流程Fig.4 IGA algorithm flow

2.2 对比试验

由图4算法设计流程可知，上述遗传算法改进的基本思想即为通过改进种群多样性来增加搜索出最优解的概率。为进一步说明改进遗传算法的实际效果，笔者从种群基因个体的近似程度、收敛效率以及曲线的梯度趋势等几个方面考虑，分别采用普通遗传算法和文中改进遗传算法，设计对比实验来验证优化算法的有效性，并绘制种群各代基因相似度曲线如图5所示。

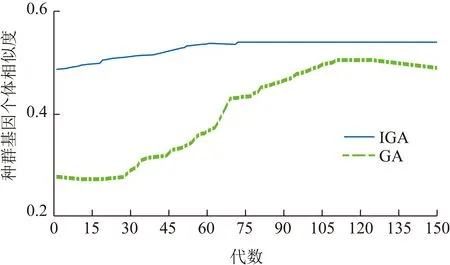
图5 种群基因相似度Fig.5 Population genetic similarity

由对比上述种群算法的迭代过程中的基因相似度可知，改进的遗传算法能大幅度提高迭代初期的种群多样性，后期种群个体差异性逐渐稳定，能有效提高算法逼近现实最优解的概率。

为进一步说明IGA算法的优化效果，文中在同一工程位置上分别采用两种算法进行仿真模拟，并绘制成本费用曲线如图6所示。

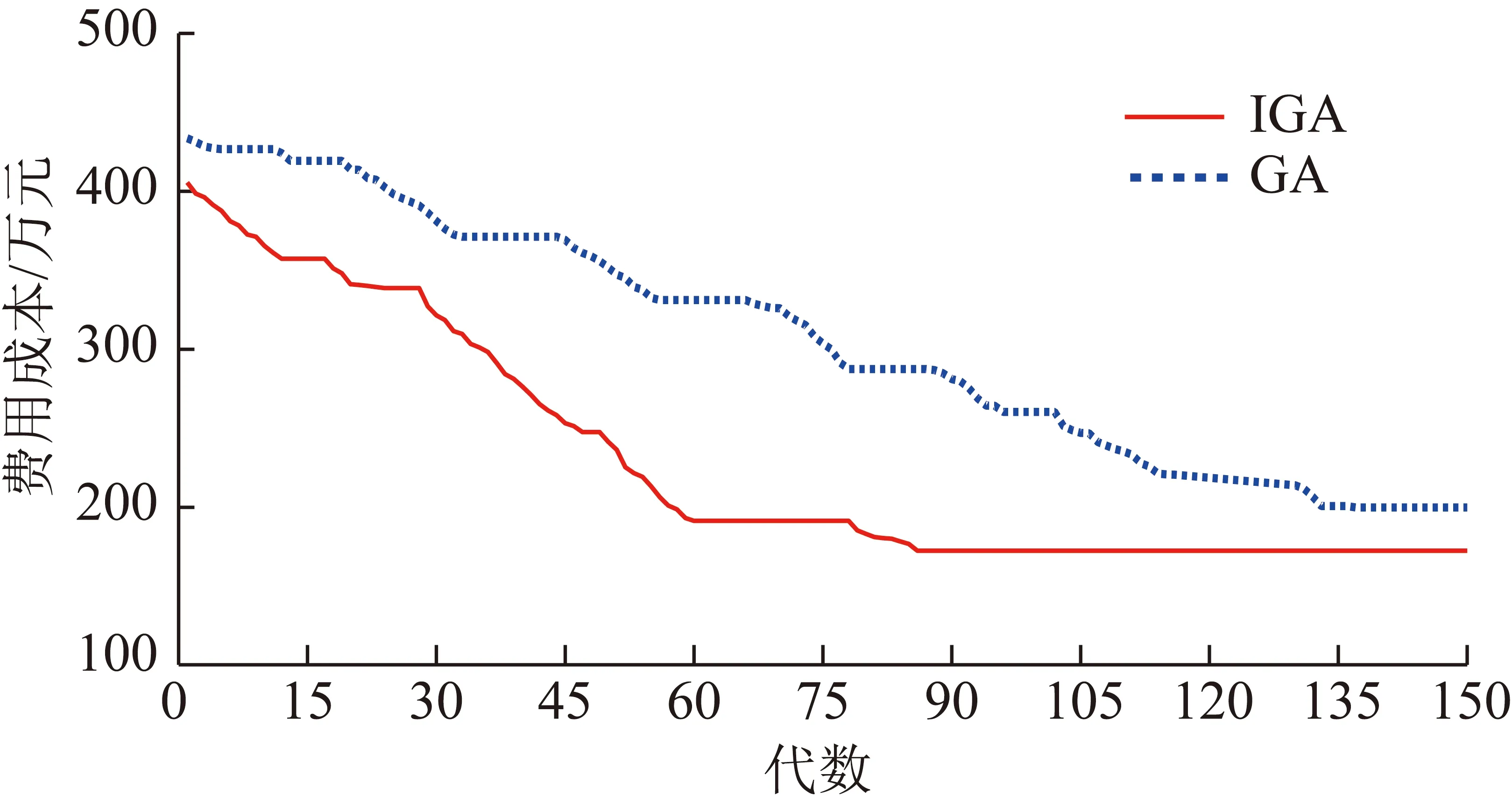
图6 GA与IGA算法费用成本对比Fig.6 Algorithm cost comparison for GA and IGA

通过对比图6中两组算法模拟的成本费用，可以看出GA算法搜索出的最优解并非全局最优解，且随算法迭代过程，频繁存在局部最优现象，且迭代效率也不如改进算法明显。

2.3 基于生物激励的启发式算法改进

综合上述分析和重复多次上述对比实验可发现，改进的遗传算法虽在一定程度上改进了种群多样性，但仍存在求解效率低、求解过程不稳定、易陷入局部最优解等问题，为有效提高算法的收敛效率和寻优能力，笔者将生物启发神经网络模型引入改进遗传算法中，试图通过其在线学习能力对算法进行启发式改进基因个体质量，从而最大程度上优化寻优过程。

2.3.1生物激励神经网络(Bio-Inspired NN)

生物激励神经网络(Biologically Inspired Neural Network)是1998年由Yang和Meng在Grossberg的生物分流模型基础上，为解决机器人动态寻径问题，提出的一种自适应的神经网络。因其网络模型中结构简单、计算任务量小、具有极强的自组织适应能力及连续光滑的有界输出，被广泛应用在机器人的三维路径规划、避障控制以及轨迹跟踪等时变动力学控制系统中，其网络的二维结构如图7所示，网络中各神经元活性的微分方程[13-16]为

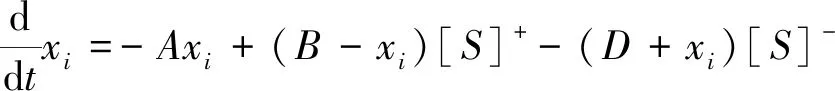
(20)

式中，xi为神经元个体的活性值;A为被动衰减率;B为神经激励活性值上限;D为神经激励活性值下限;[S]+为激励输入;[S]-为抑制输入。

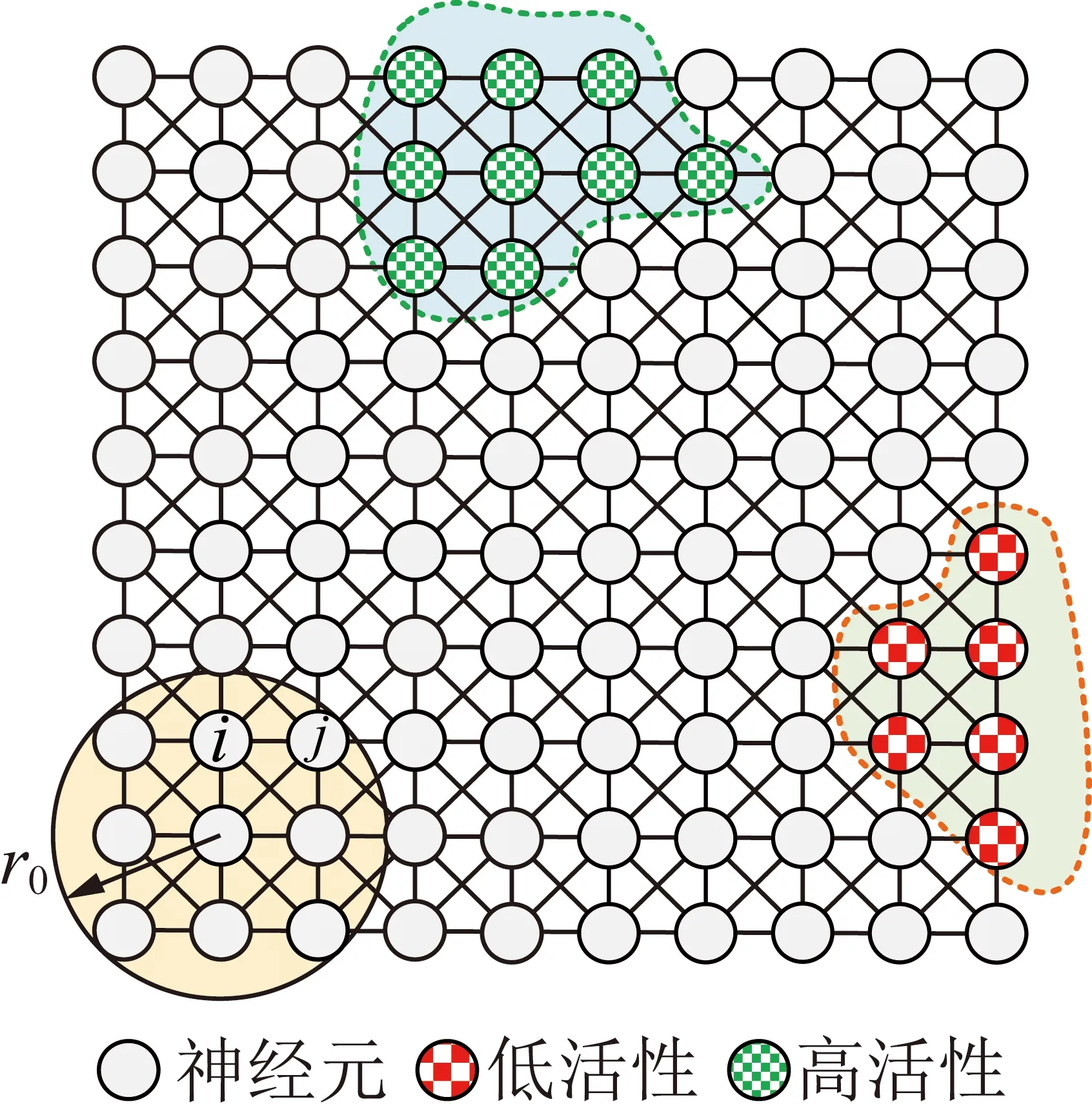
图7 生物激励神经网络二维结构Fig.7 2D structure diagram of biologic excitation neural network

2.3.2线路曲线设计算法的启发式改进

根据上文所述，当采用遗传算法进行线路的优化设计时，角度突变位置的线形设计将主要依赖于交叉、变异等基因操作来产生多样性的路径解，属于无先验的随机枚举，易产生冗余线路参与算法寻优，导致算法难以收敛于全局最优解。因此，为进一步提高算法的收敛速度及泛化能力，笔者将神经动力学模型引入种群个体的基因编码过程中，即将道路的曲线设计过程视为一种类区间匀速的动力学行为，并采用动力学的特征约束对所选路径进行判别和启发式修正。其基本原理:在每一次路径编码完成后，算法首先建立如图8所示的运动质点状态迁移模型，并利用式(21)中的神经动力学模型构造出单质点的虚拟瞬时线速度、角速度等时变状态量;结合几何设计中的参数约束，利用线速度、角速度等运动状态参量的运动学计算重新建立几何约束指标;利用速度的积分量模拟虚拟路径，最终结合网络内部构造出的虚拟误差，对基因种群实现进一步修正，从而保证每一次随机枚举所获得的路径解，均能启发式地找出满足其自身修正关系的全新路径。

(21)

式中，V为虚拟速度;[xi,yi,zi,wi]T为单质点的迁移运动；e为运动状态与运动学约束间的修正误差;exi为e在X轴向上的矢量化投影。

f(ej)=max(ej,0),g(ej)=max(-ej,0),

j=xi,yi,zi,wi

其中，Vxi,Vyi,Vzi决定了质点的线速度；Vwi决定了质点的角速度。

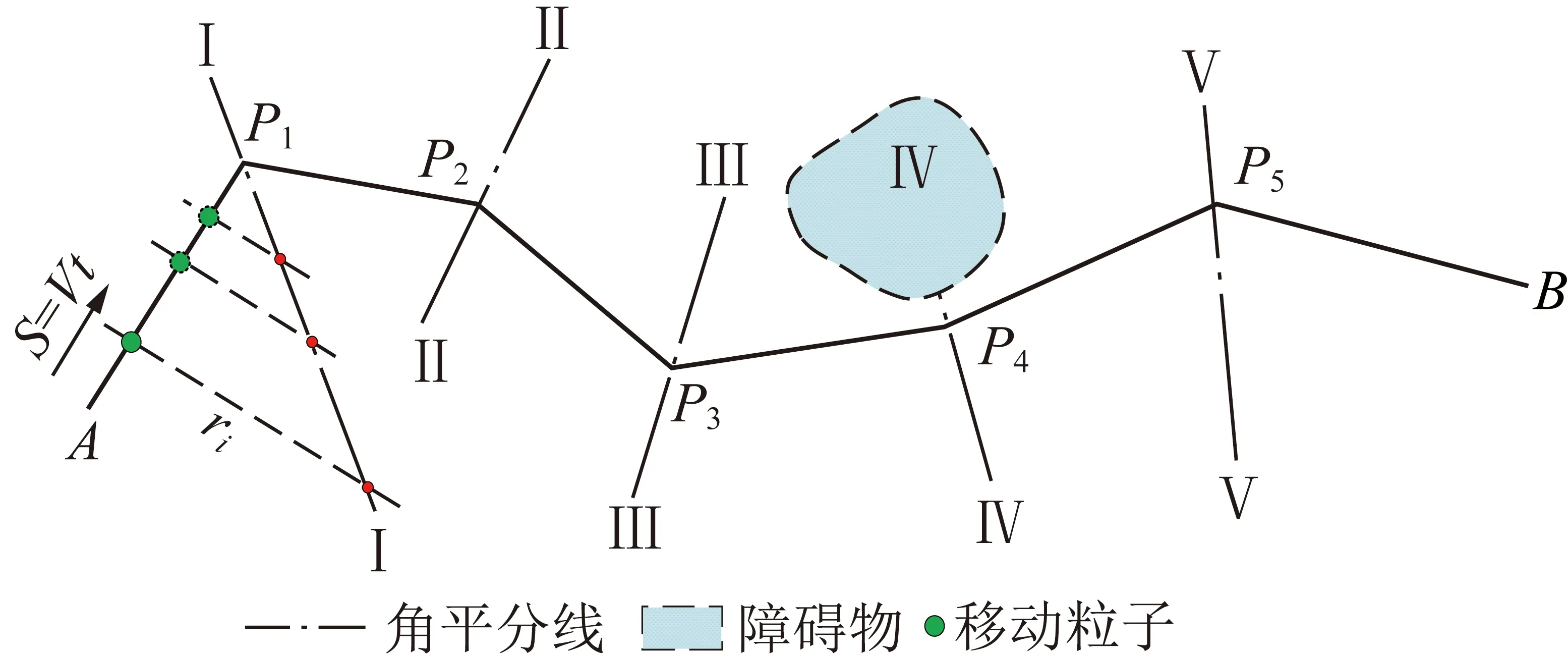
图8 时变单质点曲线轨迹状态迁移模型Fig.8 Migration model of time-varying single point curve

通过上述分析，利用神经动力学模块进行基因种群的启发式改进，主要表现在两个方面:一是生物激励神经网络可利用运动状态的迁移过程，构造出一组虚拟、有界且连续的线速度和角速度，对上述虚拟的瞬时变量的积分可构造出一条虚拟路径;二是具有启发指向性地将基因变异范围控制在误差变化速度的邻域内，提供有界且平滑的中间误差，为整个系统的误差修正提供有效的镇定输入。

具体算法工作原理如图9所示，[x,y,z]T是种群个体中的一组离散路径，利用式(21)构造出的连续、平滑的虚拟速度[Vx,Vy,Vz,Vw]，该组速度变量对时间的积分即为平滑后的虚拟路径。利用所设计的门限阈值指标对曲线设计的指标约束进行限制，并构建一组经过过滤的修正速度[Vsx,Vsy,Vsz,Vsw]T。利用上述两组速度向量，构造关于速度的虚拟误差[ex,ey,ez,ew]T，对上述误差积分便可反映出路径的运动状态变化量，以此状态变化量为变异邻域，表征路径的修正区间，最终按照修正区间进行路径修正即可自适应地构造出一组新的变异路径基因。

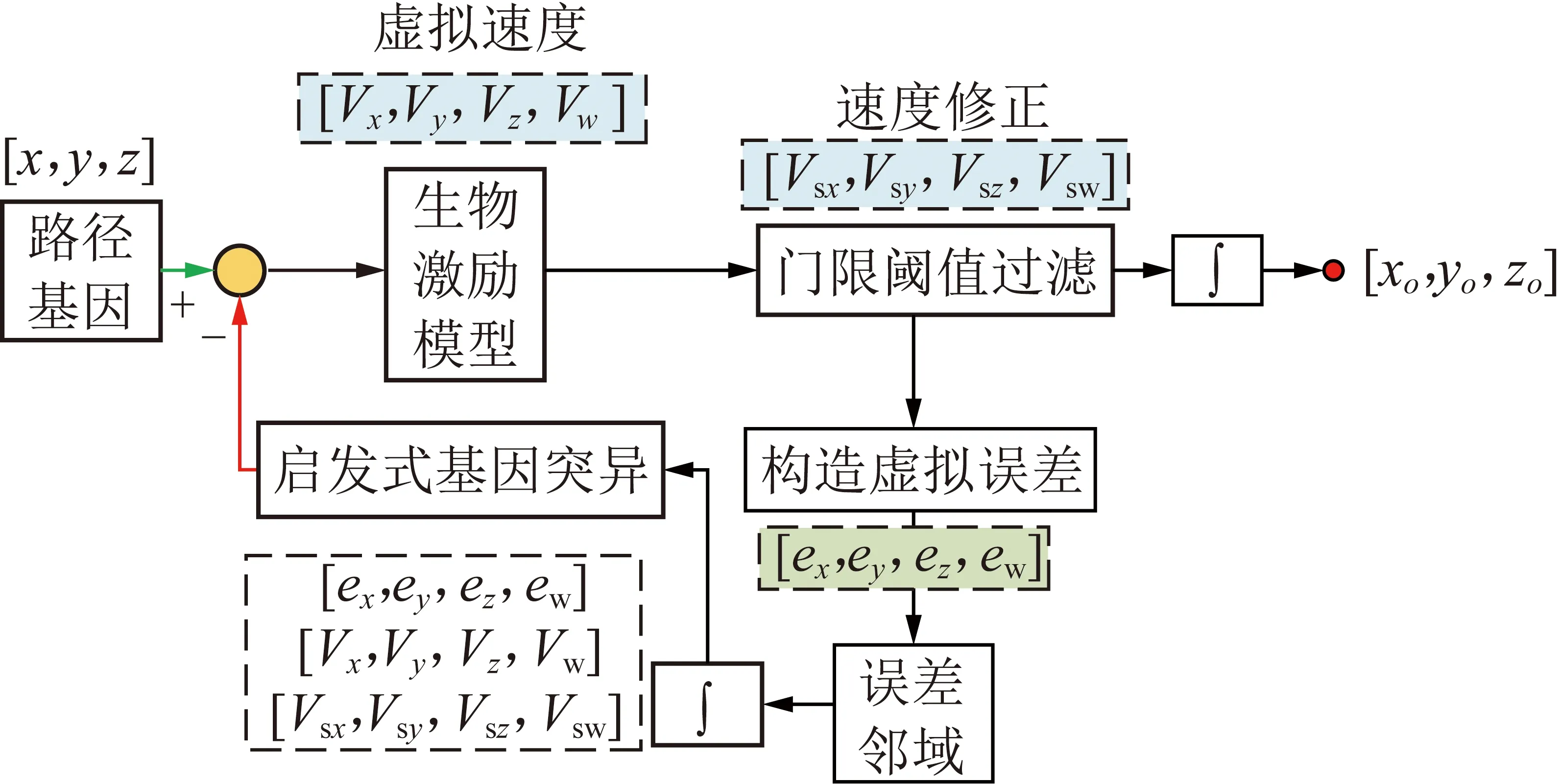
图9 启发式种群路径曲线的在线修正Fig.9 Heuristic population path curve correction

3 应用实例分析

3.1 选线算法仿真及应用效果分析

为进一步验证文中算法对于处理露天矿山选线问题可行且有效，本文以国能投新疆准东露天煤矿计划工程位置上剥离运输系统选线为研究对象，对3DMine矿业工程三维建模软件进行二次开发，以实现文中算法。利用二次开发后的运输线路优化模块对该矿2019年计划工程位置上剥离运输系统的定线实例进行仿真，其仿真优化后的开拓运输系统定线结果如图10所示。

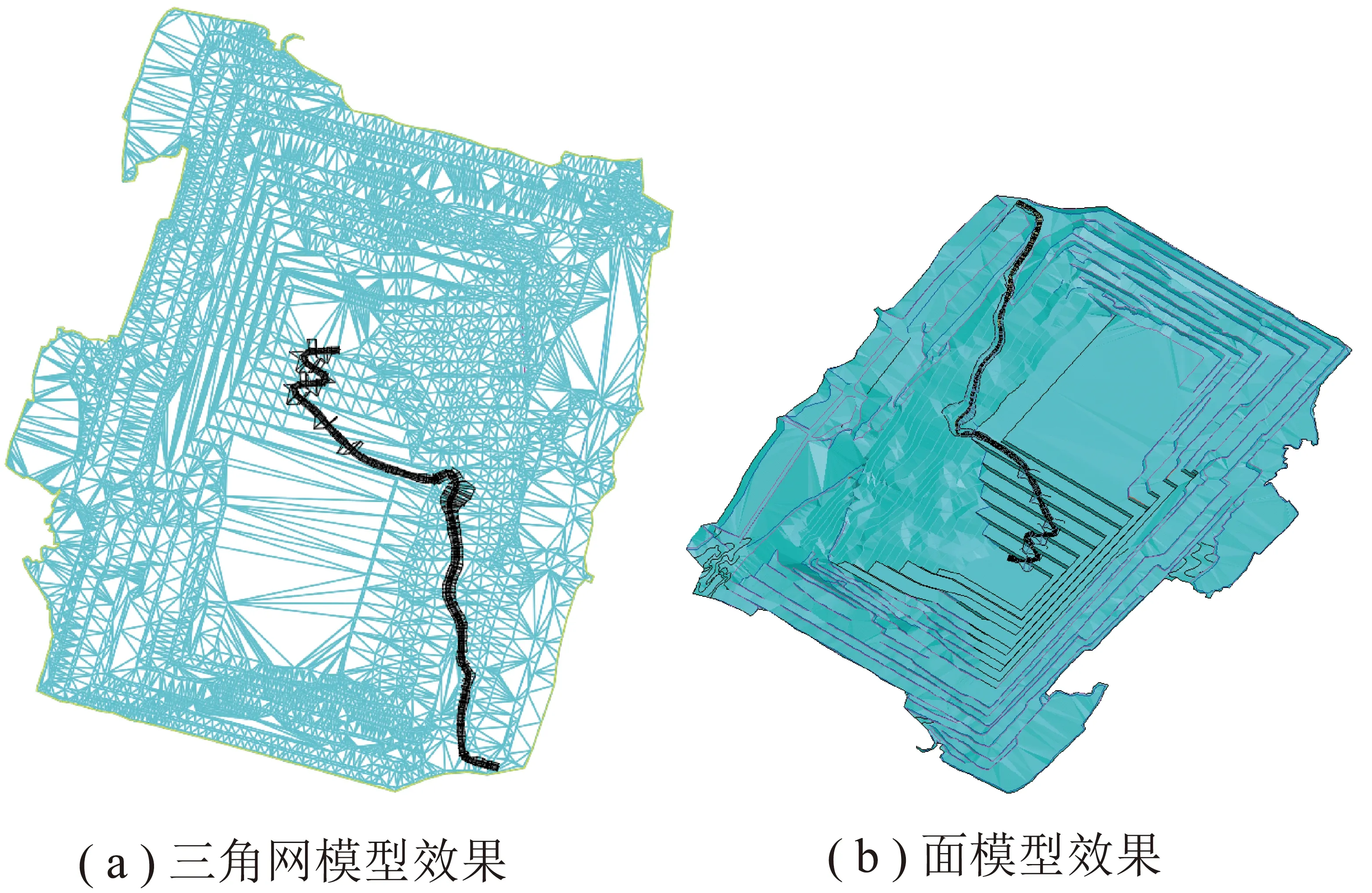
图10 选线算法三维可视化仿真结果Fig.10 3D visualization simulation results of the algorithm

为进一步体现前述算法的寻径优势，笔者采用软件内置的费用计算单元对沿用该矿现行的路径方案B(移动坑线+西-南端帮运输路线)的成本进行核算，并与图10中方案的仿真结果进行对比，利用软件输出两组路径方案随剥离物料量波动的费用成本数据，绘制关系曲线如图11所示。

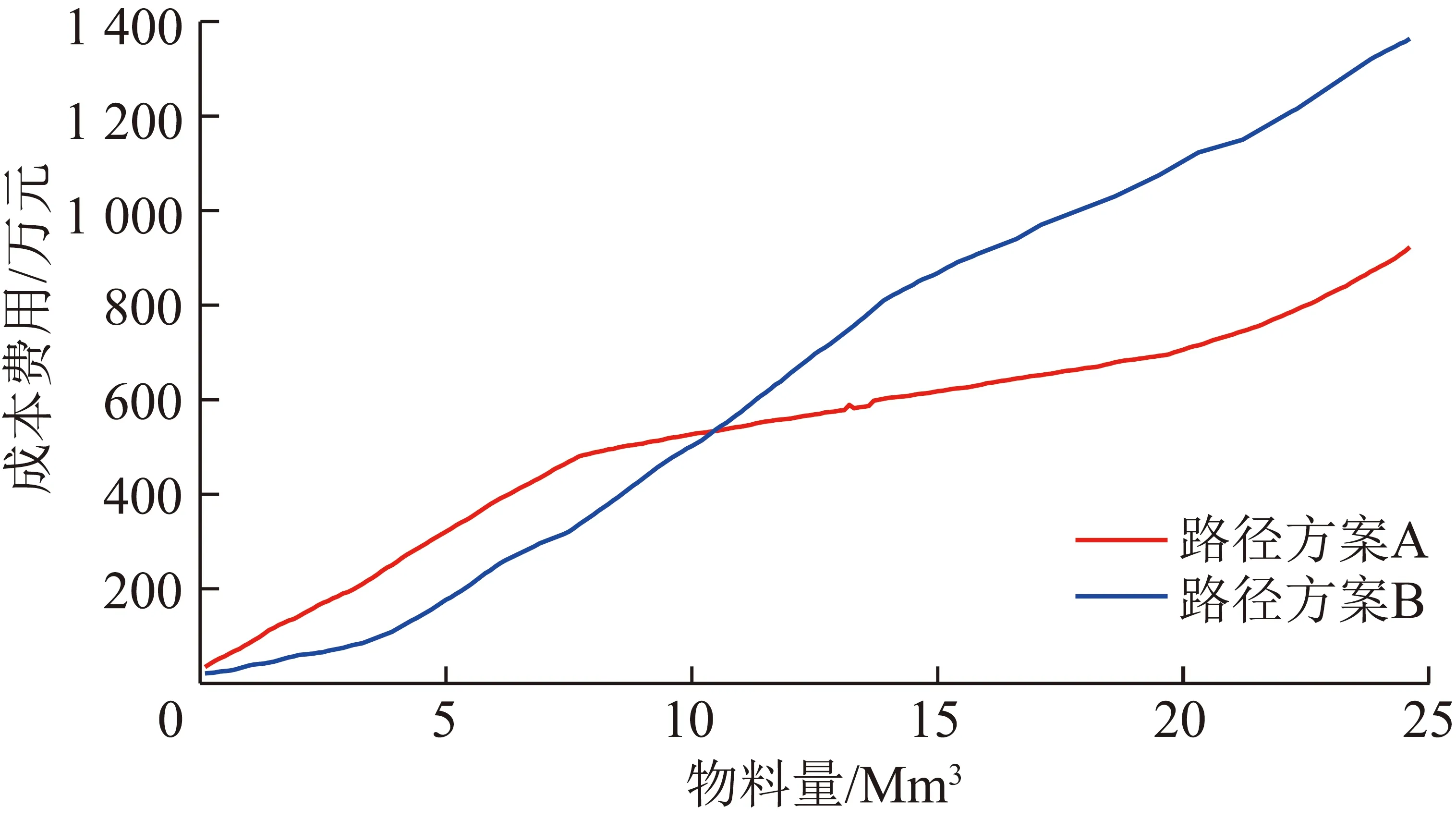
图11 不同路径方案下的成本费用对比Fig.11 Cost comparison under different route scheme

对比现实工程位置、优化出的三维线路以及图10数据可知，该矿2019年年初进度计划工程位置上，A，B两条路径方案距排土场西侧入口的线路长度分别为1.74 km和2.48 km。随着工程进度发展，A线路长度首先逐渐变短，后因需要克服高差绕行而逐渐变长，其间线路最短长度为1.13 km;而B方案线路长度则持续缩减，但因受环绕东、南端帮影响，其线路最短长度也仍需2.07 km。

因此，从路径长度上来看，软件所规划出的方案A具有明显的优势。从费用曲线对比结果来看，线路初始布设费用分别为A方案:34.63万元;B方案:21.12万元。随着后期发展A方案费用成本受运距变化的影响，增长幅度中期平稳递增，且总体费用小于方案B，最终两方案的成本核算结果分别为A方案:922.85万元;B方案:1 363.66万元。因此，A方案费用优化效果更为明显。另一方面，根据模拟开采结果，该矿自2020年开始实现内排，且外排土场开始接近最大收容量。因此，从未来纵采工程发展及布设内排线路的角度分析，方案A中的部分线路可以作为西段帮内排环线参与内排运输。因此，从未来发展角度，方案A也更符合现实工程需求。故综合上述3方面的因素，可认为方案A中规划的路径费用最优且能满足现实工程需求，具有可行性。

3.2 算法收敛性优化效果分析

为提高算法收敛性，文中将生物激励神经网络全局激励、抑制本地驻留的特性引入到IGA算法的基因编码过程中，用于启发式地提高算法收敛能力和寻优效率。因此，为验证此种启发式修正对改进遗传算法的突出作用，笔者以5组计划工程位置上的选线问题为例，采用改进的IGA算法和生物激励启发式改进IGA算法分别进行仿真模拟，其中5组工程位置上所对应的线路方案，采用图12中的5组线路来表示，即线路A～E，并通过对适应度的线性计算，统计了线路方案迭代过程中各代种群中的最优解来验证算法的收敛性和执行效率，各路径方案逐代的费用成本统计如图12所示。

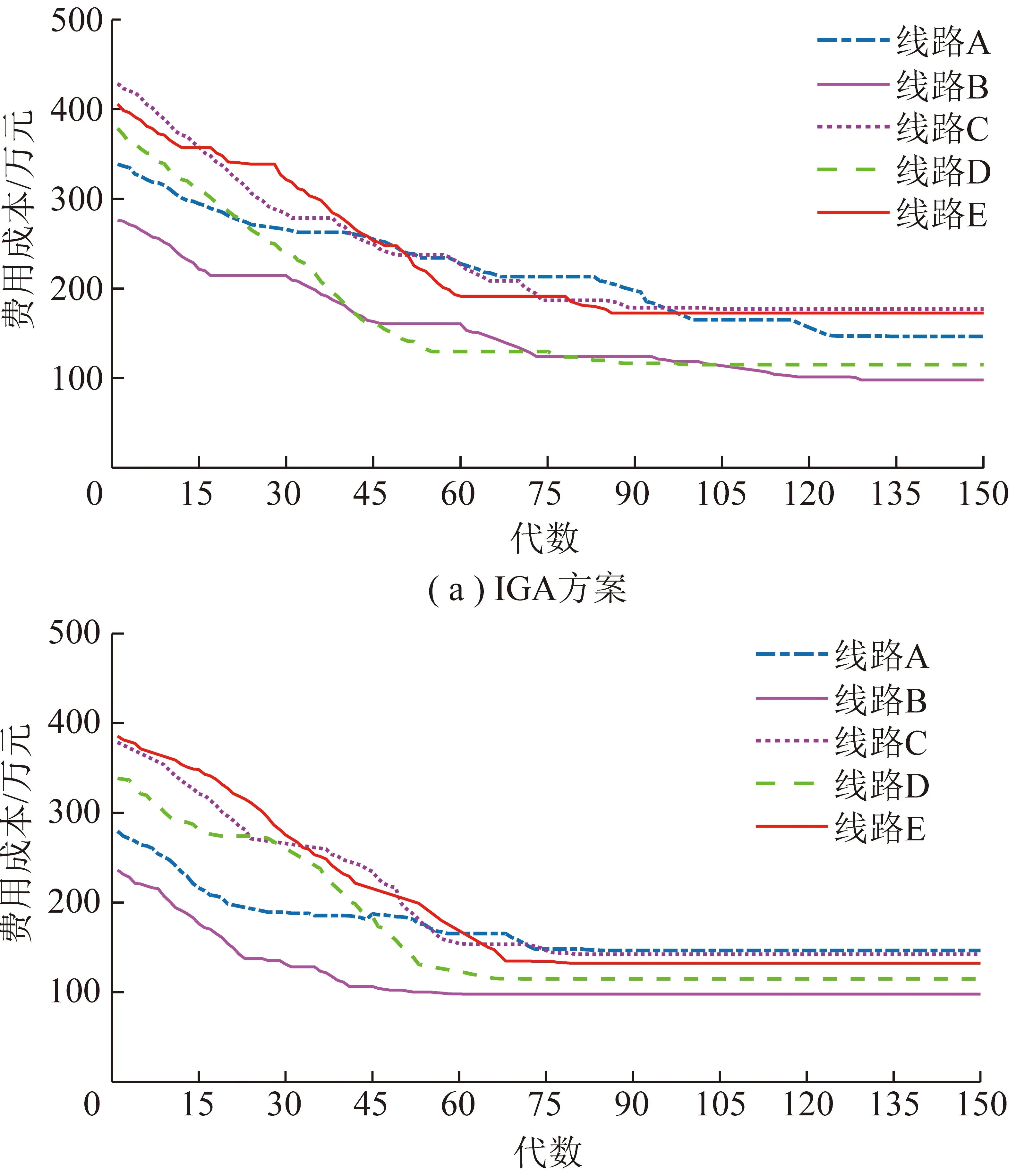
图12 线路的费用成本统计Fig.12 Route cost statistics

由图12的总体下降梯度变化来看，引入生物神经网络模型前后，曲线总体均表现出持续下降趋势，说明种群适应度在迭代过程中不断向低费用目标逼近，且父代中的优良基因能随进化过程遗传个子代个体。

进一步对比分析图12(a)，(b)，可明显发现如下差异:① 种群的进化初期，Bio-Inspired NN-IGA方案中各路线费用解收敛的最优适应度均优于IGA方案中的结果;② IGA方案中路线B、路线E均存在明显的过早熟现象，经多次重复实验验证，也均存在上述问题;③ 两种优化方案的最终收敛的最优费用解见表2，对比表2中数据可发现IGA方案中路线C和路线E存在过早熟问题，且无法收敛于全局最优解;④ 对比图12曲线可以看出，Bio-Inspired NN-IGA方案曲线具有更明显的下降梯度，并且收敛速度也明显优于IGA方案。

表2 两方案最终收敛的费用解
Table 2 Final convergent cost solution of the twoschemes/ten thousand万元

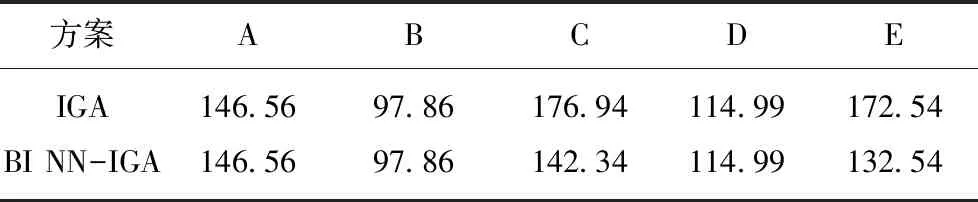
方案ABCDEIGA146.5697.86176.94114.99172.54BI NN-IGA146.5697.86142.34114.99132.54

通过上述4个方面对比分析，说明启发式改进的Bio-Inspired NN-IGA方案对于处理文中选线问题可行且有效，较之IGA算法具有更好的优化效果和执行效率。

4 结 论

(1)经典的城际高速公路定线理论中的剖面布置形式无法包含折返路径解，与矿山实际应用场景不符，无法直接应用于存在折返路径的露天矿山开拓选线问题中。

(2)以JONG的选线理论为基础，采用分阶段的选线剖面布置形式能有效解决折返路径的桩点枚举问题，并且通过坐标嵌套，计算出桩点位置坐标的代数化表达。

(3)改进的遗传算法在处理实际矿山优化选线问题时，存在无法收敛于最优解、收敛效率低下等问题，采用生物激励神经网络模型对路径基因序列进行启发式修正，能提高算法的收敛能力及效率，这种通过在线学习获得的启发式修正对于其他优化问题具有一定借鉴意义。

(4)通过费用成本对比，改进的IGA算法对于露天矿山选线问题可行且有效，对于丰富露天矿山线路工程理论具有一定的促进作用。