MRW模型参数识别的正则化方法及实证分析
侯凤仪,蒋晓颖,徐定华,3
(1. 上海财经大学 数学学院,上海 200433; 2. 浙江大学 数学科学学院,杭州 310027; 3. 浙江理工大学 理学院,杭州 310018)
经济增长理论为研究或阐述经济增长规律与影响因素的理论.经济增长具体指一个国家或地区所生产的商品和劳务能力的增长.经济学家建立各种经济模型来描述一种经济体所生产的物质商品和劳务(即实际总产出),并考察它均衡增长的条件,18—19世纪,古典经济学家亚当·斯密(Adam Smith)和大卫·李嘉图(David Ricardo)创立了古典经济增长理论,注重劳动力和资本,而知识和技术则被视为外生因素.到了20世纪50年代中期,罗伯特·索罗(Robert Solow)[1]以技术进步论为中心的新古典增长模型,指出技术进步才是经济增长的主要动力.索罗增长模型将经济增长理论研究由外生增长引入了内生增长的道路,为经济增长研究打开了一扇新的大门,之后几乎所有与经济增长有关的理论分析均以它作为参照点.20世纪90年代,格里高利·曼昆(Gregory Mankiw)、大卫·罗默(David Romer)及大卫·威尔(David Weil)[2]在证明新古典增长模型的有效性的同时,在索罗模型的基础上增加了新的变量——人力资本的积累,论证了引进人力资本增量的必要性,并且利用1960—1985年期间的121个国家的经济数据做了实证分析,为之后相关的实证研究提供了很好的起点.这个模型对现今的经济增长研究依旧具有重要的价值.例如余长林[3]通过拓展MRW模型来分析人力资本投资结构对经济增长的影响,并利用了中国29个省市的经济数据进行了实证研究;严成樑[4]也是在拓展的Mankiw-Romer-Weil(MRW)模型框架下,研究了资本投入对我国经济增长的影响,根据我国31个省的数据做了实证分析,并且估算了我国资本投资的回报率等;李强[5]在MRW模型的基础上做实证研究,将技术进步和人力资本都作为内生因子来讨论稳态增长条件.
常见的MRW模型分析都是在稳定状态下进行的,即物质资本和人力资本的增长为零,并利用线性关系式来估计参数,在进行实证研究时选择多个国家或者多个省市的数据进行回归和参数估计.本文认为估计所得的参数并不能恰当地描述多个国家和省市的真实情况.因为不同的国家不仅在技术增长率、资本折旧率等方面存在较大差异,在人力资本的结构和劳动人口增长上也各有不同.Mankiw等的文章[2]在末尾也指出未来的研究方向应是如何去解释在索罗模型中被认为是外生的变量在国与国之间为什么会有较大的差异;同时税收政策、教育政策和政治稳定性也是国家之间经济差异的重要决定因素.此外,曼昆等在论证MRW模型时利用了1960—1985年期间121个国家的数据作为样本数据,并且利用的是普通最小二乘法(Ordinary Least Squares),但是通过对论文附表数据和模型本身的分析,可以发现不仅样本数据存在缺失和可能的误差,而且在参数估计时并没有涉及到数据误差的考量和处理.
因此,本文提出一种基于MRW模型的Tikhonov正则化算法,在非稳态条件下对参数进行估计,并在实证分析时利用单一国家的时间序列数据,对单个国家的经济数据进行更合理的估计,估计随着时间推移可以灵活变动,而不仅仅是针对稳定状态.
1 反问题归结
1992年,Mankiw等[2]在索罗增长模型的基础上提出了新的MRW模型,MRW模型在索罗增长模型的基础上加入了人力资本的积累,生产函数变为
Y(t)=K(t)αH(t)β(A(t)L(t))1-α-β,
(1)
其中:Y代表产量;K代表物质资本;H代表人力资本;L代表劳动,L(t)=L(0)ent;A表示知识或者劳动的有效性,A(t)=A(0)egt;n为劳动人口增长率;g为技术进步率,均为外生参数;α和β分别表示资本产出的、劳动力产出的弹性系数.
令sk和sh分别表示物质资本储蓄率和人力资本储蓄率,δ为折旧率,资本的增长为新增资本减去折旧部分,表示如下:
(2)
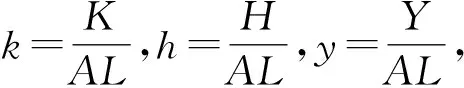
(3)
同理可以得到
(4)
根据式(1)可以得到
(5)
将式(5)代入式(3)和(4)中,则式(3)和(4)可化为
(6)
本文的反问题可以归结为: 已知k(t1)=f1,k(t2)=f2,…,k(tM)=fM;h(t1)=g1,h(t2)=g2,…,h(tM)=gM(M为正整数),来估计参数α,β,sk,sh.
2 Tikhonov正则化算法设计
首先对式(6)作线性处理,得到
(7)

通常情况下需要近似表达导数时会采用差分法,但是由于现在获得的k(t1),k(t2),…,k(tM);h(t1),h(t2),…,h(tM),为观测数据,通常存在测量误差,尤其当M的值越大,划分的间隔越小,原本测量数据的误差会在最后结果的计算中放大.所以本文采用了陆帅和王彦博[6]提出的应用Tikhonov正则化方法来估计1阶的数值微分的方法.
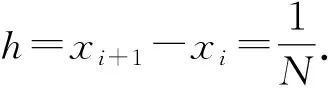
|yi-f(xi)|≤ε,
ε是测量的误差水平.现在需要估计f(x)的1阶导数.定义正则化泛函
其中:g(3)是函数g的3阶导数,λ为正则化参数.取λ=ε2(文献[7]给出了正则化参数λ的选取方法),文献[6]已证明存在唯一的函数f*∈V={h|h∈C[0,1]且h(0)=y1,h(1)=yN}满足
Φ(f*)≤Φ(g) ∀g∈V,
且构造了1个5次样条函数f*:
f*=ai+bi(x-xi)+ci(x-xi)2+di(x-xi)3+ei(x-xi)4+fi(x-xi)5x∈[xi,xi+1],
(8)
这里有6n个未知常数:ai,bi,ci,di,ei,fi,i=1,2,…,N-1.未知参数求解可参考文献[6].
反问题算法总结如下:
Algorithm1利用最小二乘法反演参数
1) 整理原始数据,给出Y(t),K(t),H(t),L(t)和A(t);

4) 输入n+g+δ,利用最小二乘法对α,β,sk,sh进行估计;
3 数值模拟与实证研究
3.1 数值模拟
为了验证算法的有效性,本文在已知α,β,n+g+δ,sk和sh的情况下,给出k(t)和h(t)的时间序列数据.然后利用这一数据,采用第2节设计的算法来估计α,β,n+g+δ,sk和sh.如果估算值和我们已知的数值相当接近,即可证明我们的算法是有效的.已知α,β,n+g+δ,sk和sh,利用Matlab中的ODE45(Runge-Kutta算法),可以求出k(t)和h(t)的高精度近似值.本文采用Mankiw等在文献[2]中对α,β,n+g+δ,sk和sh所估算的1组数据,这1组数据在原文中经过了统计检验和经济含义分析,是有效的估算结果.我们将这1组数据作为真实值,进行数值模拟的结果如表1所示.其中:R2用来衡量回归模型整体的拟合度,R2最大值为1,R2的值越接近1,说明拟合程度越好;反之,R2的值越小,说明回归直线对观测值的拟合程度越差;F是对回归模型整体的方差检验;P是判断F检验是否显著的标准.

表1 回归结果与参数估计
注: “—”表示此项无数据,下同.
从表1和图1中可以看到,2组回归估计的结果和真实值相当接近,这验证了本文算法的有效性,能够对α,β,sk,sh做出较为准确的估计.

图1 2组回归的残差Fig.1 Two sets of residual errors
3.2 实证分析
3.2.1 数据来源
1) 国内生产总值(GDP)指按照市场价格计算的1个国家(或地区)所有常住单位在一定时期内生产活动的最终成果.该指标即为生产函数的右端项,用于检验估计得到的值是否有效,是否符合MRW模型的生产函数.
2) 全社会固定资产投资是指以货币形式表现的在一定时期内全社会建造和购置固定资产的工作量以及与此有关的费用的总称.它可以用来反映固定资产投资规模、结构和发展速度.本文利用这一指标来近似替代K(t),即物质资本存量.
3) 人力资本存量的估算在学界目前没有被普遍认可的方法,常见的有“成本法”、“成本加权法”以及永续盘存法等.国内有多名学者给出了我国不同时间段的人力资本存量的估算结果.本文考虑两方面因素: 尽可能与其他指标相匹配的年份区间以及文献中估算结果的合理性分析,最终采用了乔红芳和沈利生[8]给出的1978—2011年我国人力资本存量的估算数据.他们的估算方法将直接教育、医疗保健和文教娱乐消费作为人力资本投资的成本,并创新地引入了教育投资时滞的概念,更加客观地描述不同年龄、不同学历从业人员的真实教育成本.
4) 对于L(t),选择的是国家统计局给出的经济活动人口数.该指标表示在16周岁及以上,有劳动能力,参加或被要求参加社会经济活动的人口.n采用的是经济活动人口增长率,根据L(t)的数据估计为0.008.
5) 对于综合科技水平A(t),没有找到专门的文献来对这一指标进行描述和提出估算方法.本文采取的做法是根据MRW模型中假设的A(t)以不变的速度增长,即
A(t)=A(0)egt
这一公式来进行估算.在文献[9]中,肖庭延等利用数值稳定的Marquardt算法,根据1990年全国全民所有制独立核算出的工业企业的部分投入产出数据估计出了当年的综合科技水平A(0),这一结果在文章经过各项统计检验以及经济含义的分析后证明是基本合理的.前文已写明增长速度g一般可以用人均收入的增长率来进行估算.利用国家统计局给出的城镇单位就业人员平均工资计算了我国人均收入的平均增长率,估算结果为0.135.在已知初始的综合科技水平A(0)和增长速度g后,即可得到综合科技水平的估算结果.
6) 资本折旧率根据文献[10]的数据,对选定的年份区间的折旧率取平均值,结果为0.107.
7) 原始数据误差水平并没有准确的数据,本文假设为0.01.
由4),5)和6),可以得到n+g+δ的值为0.25.最终综合所有可获得的数据,选取共有的年份区间,得到1996—2011年回归所需的基本数据.
3.2.2 结果分析
对式(7)分别做回归,可以得到两组估计值.还有一种处理办法,将式(7)中的两个等式合并成一个式子:
(9)
对式(9)做线性回归.但如果采用这种处理办法将无法求出各自的估计值.针对这两种方法本文都做了运算,希望比较一下3组回归的效果,结果如表2和图2所示.

表2 回归结果与参数估计

图2 3组回归的残差Fig.2 Three sets of residual errors

图3 Y(t)的估计值与实际值对比Fig.3 The approximation solutions and the exact soution of Y(t)

对于回归值和实际值之间的差异,一个可能的原因是原始数据没有做无量纲化处理,我们选取的指标的数量级有所不同,从而影响了结果的精度.因此对算法进行改进,添加了无量纲化的步骤.标准化公式如下:
其中:
无量纲化处理过后的结果如表3和图4所示,从中可以看出无量纲化的回归结果与实际值更为接近,整体增长趋势比较一致.而具体数值结果上,sk和sh的估计值仍然不理想.可能的原因是物质资本存量指标选取的缺陷,它和人力资本存量一样可以通过计量模型进行估算,除了固定资产投资以外还包含有其他项目,但是研究时未能获得足够长时间段的估算数据,从而利用全社会固定资产投资指标来近似替代.

表3 标准化后的回归结果与参数估计
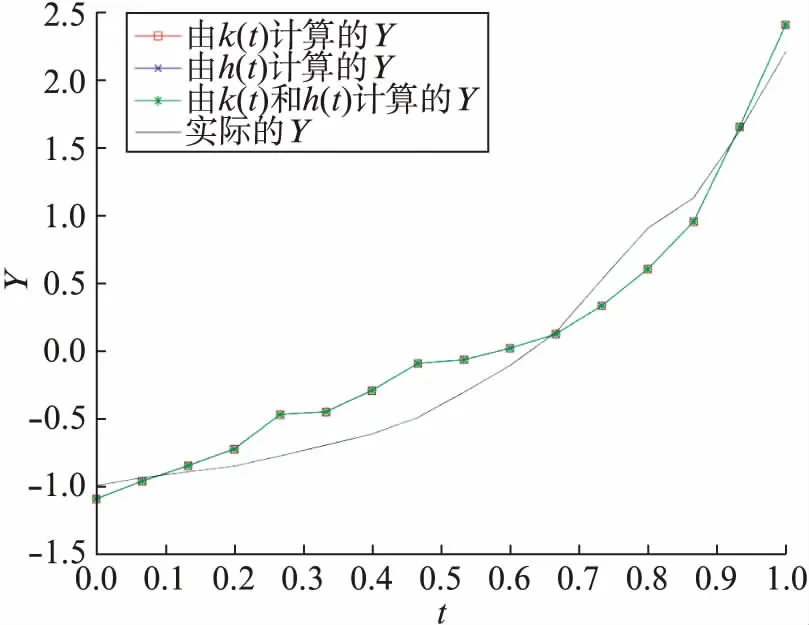
图4 标准化后Y(t)的估计值与实际值Fig.4 The approximation solutions and the exact solution of Y(t) after normalization
标准化后3组回归的结果非常接近.在未标准化时,合并两式进行回归的估计值作为结果是最为理想的,同时也验证了我们的算法是有效的,存在的缺陷是一方面没有办法分别估算sk和sh的值.当式(7)中任意一个回归出现较大的偏差,合并式(7)中的两式后的回归都会将它反映出来.如果式(7)中两式的估计效果都较为满意,可以取两次估算值的均值来达到兼顾两方数据的要求.
4 结 语
为了对非稳定状态下的资本产出弹性和资本储蓄率进行估计,本文首先利用Tikhonov正则化的1阶数值微分估算方法,然后采用最小二乘法的参数估计算法,经由数值模拟实验证明了该算法的可行性.并进一步利用1996—2011年我国的相关统计数据进行实证研究,拟合结果较好,给出的资本产出弹性估计值在经济含义上合理,进一步证明了该算法的合理性.

