云环境下中间数据集存储问题代价最小化算法研究
王莹莹 汪静 涂韬


摘要:云环境下科学工作流在运行过程中会产生大量有价值的信息以组成中间数据集,但数据集存储代价较大。因此通过阐述单云条件下线性工作流中间数据集存储问题代价最小化算法过程,指出该问题基本概念,阐明多云条件下线性工作流中间数据集存储问题代价最小化传统算法并提出改进算法,最后指出未来研究方向。
关键词:中间数据集;存储策略;代价最小化;云计算
DOI:10.11907/rjdk.192165
中图分类号:TP312 文献标识码:A 文章编号:1672-7800(2019)012-0118-04
0引言
科学工作流在科学计算时会产生大量中间数据集,研究人员可通过重新分析中间数据集得出有价值的信息用于预测,相关应用场景包括天文学领域的天气预测、高能物理学领域的微观世界探索及生物信息学领域人类遗传信息分析等。信息时代对科学计算的要求越来越高,传统网格计算无法有效支撑海量数据分析,用户可通过购买功能更强大的硬件设施,建立一个存储空间更大的网格系统,但因费用过高,系统持续性差。云计算的兴起打破了这个困局。云环境拥有大量虚拟空间,可以给用户提供廉价的资源,用户还可进行扩展,包括存储、计算和传输资源,使用极为便利。但用户在享受服务的同时也需要付出一定代价。在云环境下进行数据分析时,首要问题是代价最小化问题,即应如何处理科学计算产生的大量有价值的中间数据集,是存储、计算还是转至其它云,如何使研究者分析时有迹可循且付出代价最小,寻找中间数据集分配的最优策略至关重要。
该问题被称为中间数据集存储问题,通过对该问题的研究,可让用户得到高效服务并节省资源和费用。具体地说,单云下代价最小化算法可让用户消耗少量资源、付出最小代价得到最好服务。多云下最小化算法研究可让用户节省资源和费用,同时获得更高效的资源交流。
寻找中间数据集分配的最优决策不仅需考虑算法代价模型,还需兼顾算法高效性。袁栋等将仅涉及存储代价、重计算代价的简单代价模型改进为添加用户使用频率的代价模型,让该问题更具普适性;根据该思路,Li等对传统代价模型进行完善,建立了包含存储代价、重计算代价、传递代价、用户使用频率及用户延迟容忍度较完善的代价模型,并依据该模型设计算法得出最优策略,但算法不够高效;在处理多云条件下线性数据流的中间数据数据集存储问题时,王莹莹等有效利用并行思想优化传统算法,使算法时间复杂度由O(m4n3)降到O(m3n3),其中m表示云个数,n表示中间数据集个数;陈杰等在处理单云条件下线性数据流中间数据数据集存储问题时,通过优化存储结构,利用二叉树优化算法的存储结构,将时间复杂度由O(n2)降到O(nlgn);而在处理多云条件下中间数据集存储问题上,Xu等利用遗传算法求解,尽量将代价最小化,但最优代价准确度有待提高;陈坤针对该问题利用微积分优化算法,使最终结果更优,但是算法效率有待加强。
综上所述,云环境下中间数据集存储问题存在算法效率不高、代价模型普适性不强的问题。本文针对这两个问题的最典型解决办法进行阐述,并展望未来发展方向。
1单云条件下中间数据集存储问题Dijkstra算法
1.1算法概述
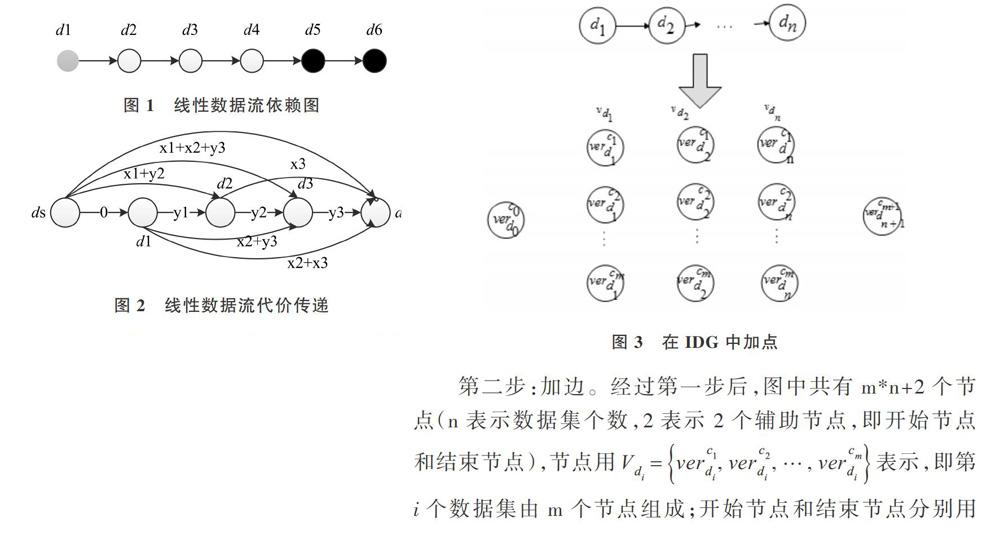
数据流中的数据集之间是单向关系,数据流依赖图(Intermediate Dataset Dependence Graph,IDG)可用一个单向无环图表示,如图1所示。
数据流依赖图经过加辅助节点ds、de及加边后,可构成数据流代价传递图(cost transitive tournament graph,CTG或CTT),如图2所示。
其中,x表示数据集重计算代价,y表示数据集存储代价,为已知数据。举例说明边权值计算过程:如ds和d2之间的边权值为d1的计算代价和d2的存储代价之和,即X1+y2,又比如ds和d3之间边权值为d1、d2的计算代价与d3的存储代价之和,即x1+x2+ys。
结合代价传递图,利用Dijkstra算法找最小代价,算法过程为:①构建代价传递图;②利用Dijstra算法找开始节点到结束节点所需的最小代价及最短路径;③输出最短路径对应的数据集状态序列(最短路径经过的点对应数据集状态为存储状态,跳过的点对应数据集状态为重计算状态)。
算法伪代码如下所示。
算法:Linear_CTT-sP
输入:开始节点ds;结束节点de;线性数据流的依赖图
输出:数据集序列
1.遍历依赖图中的每个数据集di
2.遍历di的后续节点dj
3.建边e
4.边权值初始化为O
5.遍历di和dj间所有节点dk
6.计算di和dk间边的权值
7.利用Dijkstra算法求最短路径
8.输出最短路径对应数据集状态序列
1.2算法不足之处
通过算法步骤分析可知该算法时间复杂度为O(n4);另外,在计算最小代价时,只涉及到存储代價及重计算代价,并没有考虑影响最小代价的其它因素,代价模型仍存在过于单一的问题。
2多云条件下中间数据集存储问题算法概述
2.1算法概述
多云条件下的中间数据集存储问题涉及的基本概念与单云条件下中间数据集存储问题类似,本部分阐述在多云条件下,数据流依赖图构造代价传递图的过程。
第一步:加点。在原依赖图中根据云的个数加点。每个节点被拆分成多个节点,拆分成多少个点由云的个数决定。如图3所示有m个云,每个节点被拆分成m个节点。
2.4算法不足之处
改进后的算法通过先计算最长边权值并同时存储中间结果的方式,有效避免了传统算法的冗余计算。具体指通过分析5~27行代码,可知计算每条边的权值时间复杂度由0(m2n)降到O(mn),从而算法整体时间复杂度由O(m4n4)降到O(m3n3)。
然而,代价模型方面仍存在弊端,多云条件下中间数据集存储问题代价最小化算法涉及的代价模型除了有存储代价和重计算代价及云之间的传递代价外,并没有考虑其它影响因素,如用户容忍度与数据集使用频率等,严重影响到算法模型普适性。
3结语
为解决云环境下中间数据集存储代价最小化问题,本文通过介绍单云条件下中间数据集存储代价最小化问题,引出该问题基本概念,并指出目前单云条件下线性数据流存储问题解决方案中存在代价模型普适性较差的缺陷,阐述了在单云延伸到多云条件下线性数据流中间数据集存储代价最小化问题,通过与传统方法对比分析,设计出优化算法并进行了数学证明,但该算法缺乏实验数据支撑,下一步将致力于对算法的实践验证。

