混流法式水轮机调节系统非线性建模与分叉分析
张记坤 曾云 王芳芳 杨光波 张振凯 钱晶


摘要:基于Matlab仿真软件,考虑弹性水击对水轮机调节系统的影响,建立弹性水击水轮机微分代数模型,并与调速器和发电机共同构成水轮机调节系统非线性模型。在此基础上运用非线性动力学分叉理论对PID调速器参数进行Hopf分叉行为研究,得出PID参数三维分叉曲面、二维分叉曲线及稳定域,并通过对时域图、相轨迹图等的综合分析,得到取不同调速器参数时系统的非线性动力学特性,为机组PID参数选择提供理论依据。最后通过系统仿真得出,在小扰动下线性模型和非线性模型均能适用,在大扰动下非线性模型能更真实地反映机组动态特性。
关键词:弹性水击;非线性模型;Hopf分叉;分叉曲面;动力学特性
DOI:10.11907/rjd k.191317
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2019)012-0102-06
0引言
水轮机调节系统是由压力引水系统、调速器、水轮机、发电机以及所在电网组成的包含水、机、电的复杂综合闭环控制系统,其中调节对象为复杂的非线性、非最小相位系统,且在不同工况下,各环节惯性常数与系统参数均有所不同。传统对水轮机调节系统的分析多是采用刚性水击假设条件下的水轮机线性模型,而忽略了管道弹性作用及系统的非线性属性,对于小波动扰动暂可用来分析其动态调节过程,但随着机组压力引水系统越来越复杂,管道的弹性水击效应不能被忽视,同时由于调节对象的非线性特性,运用刚性水击线性模型研究机组调节动态不利于系统安全稳定运行方案的实施以及控制规律的优化设计。基于此,本文在文献[8]给出的管道弹性水击数学模型基础上,将该模型转化为非线性微分方程形式,而水轮机出力采用IEEE提出的非线性模型代数方程,二者共同构成水轮机的微分代数系统模型,并结合发电机一阶模型与PID调速器一起组成水力发电机组的非线性调节系统。
针对非线性问题的研究,常用方法有微分几何理论、分叉理论、混沌理论、模糊理论等。其中Hopf分叉理论是非线性动力学中一种分析系统参数对系统稳定性影响的重要方法,是一种局部的动态分叉理论,具体是指随着分叉参数的变化,系统在平衡点处突然分叉出极限环的现象,被广泛应用于各类复杂的非线性动力学问题研究中。本文运用Hopf分岔理论对构建的非线性调节系统模型在频率扰动和负荷扰动两种工况下进行分叉分析,得出PID参数在空间中的分叉临界曲面、二维分叉曲线及系统稳定域范围,并深入研究了当调速器参数变化时系统的动态特性,为调速器参数选择提供理论参考。
1水轮机调节系统非线性模型
单机单管、无调压井水轮机系统非线性模型如图1所示。其中,y为导叶开度相对值;q为水轮机流量相对值;qn1为水轮机空载流量相对值;qo为水轮机初始工况流量相对值;h为水轮机水头相对值;hq为水轮机暂态水头相对值;f为水头损失系数;At为水轮机增益,一般为常数;pm为水轮机出力相对值;D为水力阻尼因子。
管道动态是指水轮机流量变化引起的水轮机水头变化。对照图1可知,水力系统传递函数是从流量变化q到水轮机暂态水头△hq的变化,根据文献[8]提出的弹性水击传递函数模型,并依据文献[23]中对于n取高阶时的对比研究,弹性水击时n取1已能满足研究要求,故n=1时弹性水击传递函数为:
该模型综合了水机电过程中各因素的相互作用,且模型物理意义清晰、适用范围广,在一定程度上反映了机组的非线性特性。
2Hopf分叉直接代数判据
在该曲面上任取一点,kp=1.5,Ki=1.083,kd=0-3,仿真结果如图4所示。由图可知机组此时处于周期等幅振荡状态,振荡周期约为14.3s,相轨迹图出现稳定的极限环。所以在参数选择不恰当时,系统可能出现持续的等幅振荡,使机组难以稳定。
在分叉曲面或曲线上下方区域各取数点进行动态仿真,得出机组的转速偏差时域图、导叶开度偏差时域图、流量变化时域图以及相轨迹图,深人探究机组在该区域的稳定特性。现取曲面上方任意一点,kp=1.5,Ki=1.15,kd=03,各参数变化如图5所示。
同时,在分叉曲面上方再任取一点,kp=1.5,Ki=1.25,Ka=0.3,各参数变化如图6所示。
由图5、图6可知,在分叉曲面或Kd=0.3分叉曲线上方取点,机组各参数均处于发散状态,所以曲面或曲线上方区域为不稳定区域。由各参数偏差幅度来看,距分叉曲面或曲线越远的点,机组不稳定程度越大。
由图7、图8可知,在分叉曲面或Kd=0.3分叉曲线下方区域,机组各参数均处于收敛状态,所以曲面或曲线下方区域为稳定区域,且距分叉曲面或曲线越远,机组稳定速度越快,所以调速器参数应在远离曲面的区域进行选择。同时由图3可知,随着微分增益的增加,系统的稳定域范围逐渐扩大,表明PID调速器的微分环节有利于保持非线性系统的稳定性,与微分环节的作用相符。
扰动值△mg=1,r=0。由此可计算出非线性系统的平衡点为(088,0,0,0,0.88,0.88/K,),将平衡点代人公式可计算出该系统在平衡点处的Jacobi矩阵及其特征多项式,进而代入Hopf分叉判据,可得在机组由空载到额定负荷过程中PID参数三维分叉曲面以及二维分叉曲线,如图9、图10所示。
同理,在该曲面上任取一点,Kp=1.5,ki=1.1418,kd=0.3,机组转速变化时域如图11所示。由仿真曲线可知,此时机组处于等幅振荡状态,振荡周期约为14.3s,与频率扰动下机组振荡周期基本一致。
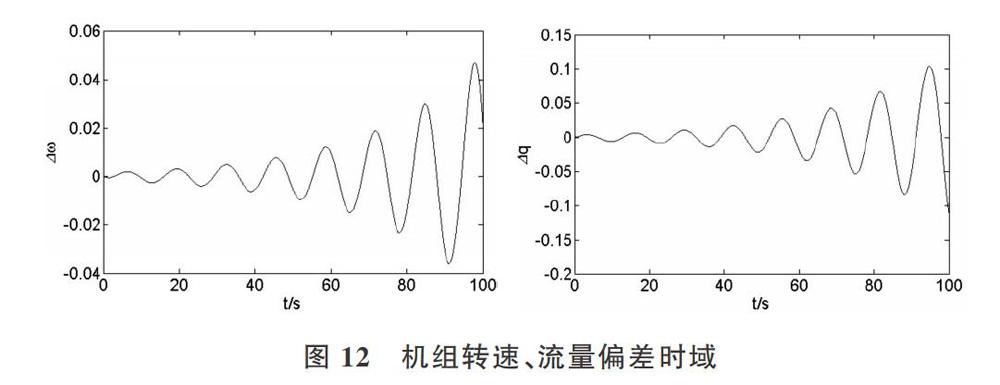
同时,在该分叉曲面上方任取一点,kp=1.5,Ki=13,kd=0.3,仿真结果如图12所示。此时机组转速变化与水轮机流量变化随时间推移作周期增幅振荡,此时机组处于不稳定状态,所以分叉曲面上方为不稳定区域。
同時,在分叉曲面下方任取一点进行仿真分析,kp=1.5,ki=0.8,Kd=0.3,如图13所示。由图可知,此时机组转速和流量变化逐渐趋于稳定。由于管道较短,摩擦损失小,故水轮机水头稳定后变化不大,水轮机出力由空载时的0增加至额定负荷,此时机组处于稳定状态。
3.3频率扰动与负荷扰动分叉图对比
频率扰动和负荷扰动是机组在运行过程中最常见的两种工况,也是机组进行稳定性试验不可或缺的两种试验方式,所以在机组进行频率和负荷调节时,调速器参数选择是否合理对于机组稳定性有着十分重要的影响。故将机组进行频率扰动及负荷扰动下的调速器参数分叉曲面与分叉曲线进行对比分析,如图14所示。
由图14可知,在频率和负荷两种扰动条件下,调速器参数所构成的分叉曲面形状相似,分叉曲线变化一致,且下方区域均为稳定域。但在频率和负荷扰动下的稳定域范围略有差异,在负荷扰动下的稳定域范围略大。理论上而言,为保证两种扰动下机组均处于稳定状态,在调速器参数选择时应尽量在频率扰动下的分叉曲面或曲线下方区域进行选择,才能在频率和负荷扰动下均获得较好的控制效果。
3.4模型对比
水轮机调节系统分为线性模型和非线性模型,理论上而言,当机组受到小扰动时,线性模型基本能满足仿真要求;当机组受到大扰动时,线性模型已不能满足仿真对精度的要求,需要建立非线性模型。所以为了探索两种模型在不同扰动下的动态特性,分别对减10%、20%、50%负荷扰动下的机组过渡过程进行仿真,机组转速偏差响应曲线如图15所示。由图可知:在减10%以及20%负荷小扰动工况时,两种模型的过渡过程基本一致,说明非线性模型也适用于机组的小扰动工况;在减50%负荷大扰动暂态过程中,线性模型过渡过程的振荡次数不变,稳定时间也基本一致,这与实际情况有所出人。非线性模型中机组过渡过程的振荡次数发生了变化,稳定时间也不同,这是调速器在受到大扰动时的快速动作导致的,与实际情况吻合。所以在大扰动过渡过程中,非线性模型更能真实反映机组动态特性。
4结语
本文基于Matlab仿真软件建立弹性水击传递函数,并建立水轮机调节系统非线性微分代数模型。以PID调速器参数作为分叉参数,运用分叉理论讨论了混流式水轮发电机组在频率扰动和负荷扰动两种工况下机组调节系统的Hopf分叉现象,得出PID参数三维分叉曲面、二维分叉曲线及稳定域,为机组PID参数选择提供了理论参考。同时分析了在频率和负荷扰动下所构成分叉曲面的稳定域范围,得出在选择调速器参数时,应尽量在频率扰动下的分叉曲面下方区域进行选择,才能在频率和负荷扰动下都获得较好的控制效果,但具体参数选择仍要结合机组实际情况综合考虑。最后仿真了在两种模型下,机组受不同负荷擾动时机组转速变化情况,得出在小扰动工况下两种模型均适用,在大扰动工况下非线性模型更能反映机组实际情况。

