基于随机游走增强型矩阵分解的混合服务预测
林坚 李俊


摘要:随着Web服务数量的急剧增长,如何在大量功能相似但非功能属性各异的服务中选择满足用户个性化需求的服务是亟需解决的问题。基于QoS(Quality of Service)预测的服务推荐方法成为研究热点。然而,QoS数据的稀疏性和“冷启动”问题阻碍其发展。针对当前主流的QoS预测模型预测精度不高和收敛速度较慢等问题,提出一种基于随机游走模型和矩阵分解技术的混合QoS预测方法。该方法首先基于矩阵分解获得用户及服务的潜因子矩阵,并将用户潜因子矩阵转化为用户相似度矩阵;然后基于用户相似度矩阵并结合Web服务的网络位置信息,使用随机游走模型提高用户相似度矩阵的准确性;最终结合协同过滤方法与矩阵分解模型进行QoS预测。在真实数据集上实验,结果表明,与当前主流的QoS预测方法相比,该方法具有更高的预测精度和效率。
关键词:QoS预测;随机游走;矩阵分解;混合预测;服务推荐
DOI:10.11907/rjd k.191205
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2019)012-0082-07
0引言
近年来,基于协同过滤(cF)和矩阵分解(MF)的推荐模型在传统推荐领域如商品、音乐和电影的推荐中应用广泛。然而,由于Web服务环境下QoS数据难于收集,并且数据存在稀疏性及收集数据中存在大量无法用于预测的无效信息等原因,阻碍了服务个性化推荐领域的发展。此外,Web服务分布在不同异构网络中,这些网络性能各异且独立的自治系统所收集的数据,通常受网络位置影响而出现偏差甚至无效,从而无法进行有效的QoS预测。因此,亟需一种能针对上述问题的、高效准确的Web服务推荐方法,以满足用户的个性化需求。尽管目前已经存在许多基于QoS预测的服务推荐模型,但普遍存在预测精度不高、模型复杂等问题。
近年来,基于QoS预测的Web服务推荐技术得到了迅猛发展。传统的QoS预测方法包括基于历史记录的QoS预测方法、基于位置感知的QoS预测方法、基于时间感知的QoS预测方法以及基于服务外部信息(IP或GPS)的QoS预测方法。虽然这些方法所使用的服务领域信息对QoS预测至关重要,但是由于QoS数据集的稀疏性所导致的领域信息不平衡,使得这些方法在提高QoS预测精度上作用十分有限。基于矩阵分解的QoS预测模型能在一定程度上缓解数据稀疏性带来的问题。文献[8]提出一种基于矩阵分解的协同过滤方法预测缺失的QoS值,但该方法存在局部预测精度难以提升问题;文献[9-10]提出了基于随機游走的QoS预测模型,并验证了模型在真实QoS数据集上能相对有效地提高预测精度。模型的主要思想是利用转移概率矩阵和马尔可夫随机过程原理,把无直接关系的用户之间相似度考虑在内,以在稀疏数据集上获得更加准确的相似性,但该方法存在全局预测精度难以提升的问题。
针对当前预测模型存在的问题,本文结合现有预测算法优点,并且针对QoS数据集特点,提出一种混合型预测算法以提高QoS预测精度。
1相关工作
1.1问题描述
基于QoS预测的Web服务推荐主要思想是预测用户未曾调用过服务的QoS值,并基于所预测的QoS值推荐能满足用户个性化需求的服务。实际Web服务QoS预测场景中包括用户、服务、用户调用服务的实际QoS值3个角色,可用G=(US,SS,Q)三元组表示,其中US={u1,u2,...,,um}表示所有用户的集合,SS={S1,S2…Sn}表示所有服务的集合,qij,∈ Q表示用户i调用服务j产生的QoS值(如响应时间、吞吐量等)。如果服务i未曾被用户i调用过,则qij为空,否则非空。一般qij,=-1表示无效值,QoS预测问题是对所有qij为空或无效值进行预测并填充。
1.2冷启动与稀疏性
传统的基于协同过滤(cF)的QoS预测方法会面临“冷启动”和稀疏性问题。其中“冷启动”问题表现为新的服务或用户没有历史调用的数据可利用,从而无法对此类用户或服务进行推荐。数据稀疏问题表现为当用户和服务数量急剧增长时,某个用户只调用过其中少部分服务,或某个服务只被其中少部分用户调用过,导致被观测和记录的QoS值qij只占整个二维矩阵Q很小部分,从而无法进行有效预测。
1.3矩阵分解方法
基于矩阵分解(MF)的QoS预测方法是当前解决“冷启动”和数据稀疏性问题的主要途径。矩阵分解方法主要思想是基于机器学习方法,将表示原始数据集的二维矩阵Q分解为用户和服务的潜因子矩阵u和s,其中所有Uij和Sij都不为空。然后根据潜因子矩阵中行列之间的线性相关信息恢复原矩阵Q中缺失的值。
尽管矩阵分解方法能够挖掘出用户服务间的潜在信息,但仅依靠行列之间线性关系得到的QoS预测会较粗糙,且会引入大量噪声。另外,全局性好的矩阵分解方法对局部数据不够敏感,会遇到局部预测精度难以提升问题。
1.4随机游走方法
基于随机游走模型的QoS预测方法能够增强用户之间的相似性,从而在一定程度上提高服务预测的准确性。该方法是传统CF模型的一种重要改进,其主要思想是利用转移概率矩阵和马尔可夫随机过程原理,把无直接关系的用户之间的相似度考虑在内,以在稀疏数据集上获得更加准确的相似性。但传统的随机游走模型简单地在原始用户相似度矩阵上进行随机游走,并没有把Web服务的领域信息考虑在内,且没有利用QoS全局范围内的信息进行预测,因此预测精度提高有限。
1.5Web服务领域信息
在动态开放的服务环境中,QoS通常会受到用户和服务领域信息如网络位置等影响。因此,在QoS预测时还需将服务的领域信息考虑进来。可以利用原始QoS数据集中存在的AS1={asi1,asi2...asik}属性表示用户或服务的位置系统编号,例如asi;表示用户i的位置在系统j中。CAS(ui,uj)∈A表示User,和User,的公共位置系统。附加的CAS数据集会给稀疏的QoS数据集带来更多的领域附加信息,能够提高QoS预测算法的准确率。然而,在用户和服务位置分布比较稀疏的情况下,传统的基于位置的服务推荐方法在服务QoS预测精度方面会受到限制。
2QoS预测方法
为提高服务预测算法的精确度和效率,在充分分析上述模型的优缺点以及QoS数据特点基础上,首先利用矩阵分解模型得到全局范围内准确性较高的QoS预测值;然后基于矩阵分解得到用户隐特征矩阵,结合Web服务的网络位置信息进行随机游走以增强用户之间的相似度,进而在局部范围内增加QoS的预测精度;最终混合上述步骤得到两种不同的结果作为最终的QoS预测值。
3RWEMF模型
针对QoS预测中存在的稀疏性问题和“冷启动”问题,本文提出一种结合矩阵分解方法和基于Web服务领域信息的随机游走模型混和的QoS预测方法(RWEMF)。该方法首先通过矩阵分解得到用户潜因子矩阵,然后基于用户潜因子矩阵进行相似度计算得到用户相似度矩阵,在此基础上结合Web服务的领域信息基于随机游走模型增强用户间的相似关联度,最后混合协同过滤和矩阵分解得到最终QoS预测值。
3.1矩阵分解求隐含矩阵
矩阵分解是一种基于低秩矩阵恢复的方法,在服务推荐领域已经得到广泛应用。它通过将用户和服务投射到更能体现其最显著特征的具有更低维度的隐含空间,解决有限覆盖和稀疏性问题。
显然,矩阵分解能解决大量QoS值为空的稀疏问题,并且能在短时间内有效处理大量的服务数据。然而,基于矩阵分解的模型是在全局范围内对缺失Qos值进行填充,并没有考虑用户的个性化程度及不同偏好。因此对于稀疏数据集上的用户,预测值将接近区域服务的平均值,并且对数据集中波动较大的用户和服务的预测准确性会降低。因此考虑在矩阵分解的基础上结合协同过滤方法进行个性化的Qos预测,以增强预测结果的准确性。
3.2相似度计算
传统的CF方法基于原始数据集并采用Pearson相关系数(PCC)计算用户之间相似性,如公式(5)所示。PCC反映了不同用户的QoS值记录的线性相关性,这种相关性反映了用户之间偏好的相似性,假设用户偏好长时间保持不变。
尽管构建用于推荐的相似性矩阵较容易,但是存在这样的问题:当两个用户没有共同调用的服务时,距离将为零。因为较低距离值意味着算法中的用户之间有更多相似性,所以零距离用户被视为最相似的用户,并且将选择作为最终预测的邻居。另外,基于CF的方法中的相似度计算并不总是有效。当服务数量很大且QoS值为空时,大量的计算资源被浪费。因此,与传统CF方法不同,使用上一步骤矩阵分解方法后得到的用户潜因子矩陣u计算用户的相似度,由于u比原数据维度较小并且不存在缺失数据,因此大大节省了大规模数据集运算时间,提高了相似度计算的有效性。相似度矩阵Sim计算如下:
其中,参数0<λ<1用于调整各部分预测结果的权重,使得模型适应不同场景。该算法考虑用户在QoS值中的均值偏向Q,结合MF具有较好的全局预测能力,两个模型在过拟合或欠拟合预测过程中由混合算法的参数协调以取得更高精度。
3.5算法复杂度
RWEMF模型的预测算法时间复杂度由CF和MF各自的计算过程组成。其中,CF的时间复杂度从O(m×n×n)降低到O(m×n×K),其中K是矩阵u的隐含维度。当n很大并且K很小时,计算时间将在数据量大的数据集中得到有效节省。从整体过程看,RWEMF算法在这些Web服务数据集中不会增加额外的时间复杂度。尽管其时间复杂度大于RWE和MF的总和,但其运行时间即使在数据量大的Web服务数据集上仍在可接受范围内。
4仿真实验
4.1实验设置
本实验采用真实数据集WS-DREAM对模型有效性进行验证。整个数据集包括两个子数据集:响应时间(RT)和吞吐量(TP)。其中响应时间单位为秒(s),吞吐量单位为千比特每秒(kbps),数据集详细的统计特征见表1。从表l可以看到数据集的基本情况,参加统计的数据包括339个用户和5825个服务,其中统计参数包括最小值(min)、最大值(max)、平均值(mean)、标准差(std)。可以看到RT较TP数据集具有更小的数据跨度和较小的方差。在两种分布各异的数据集上进行实验能充分反映预测方法在一般情况下的性能。
表2显示有关用户和服务位置信息。user_as行表示数据集中有339个用户,分布在136个领域中,每个领域至少有1个用户,不超过31个用户。一个领域内平均用户数为2.4745,标准差为2.8338。service_as行表示数据集中有5825个服务,分布在992个领域中。每个领域至少有1个服务,不超过1212个服务。一个领域内的平均服务数为5.8660个,标准差为40.6090。其中,后缀“as”和“ct”分别表示领域为as(自治系统)和ct(国家)。
本实验算法采用python2.7和c++混合实现,在一台CPU为Intel Core i585002.8GHz、内存为8G的PC上运行,操作系统为Ubuntu 16。
MAE反映预测的绝对误差,NMAE反映预测的相对误差。通过MAE与NMAE两个参数的比较可以反映出预测算法的预测精度和性能。
4.3预测准确性
与几种当前主流预测模型进行对比验证RWEMF模型的有效性。
(1)UPCC是一种基于用户的协同过滤算法,通过Pearson相关系数计算用户之间的相似度,以用户间协同关系为基础提供其他用户QoS值的预测。
(2)IPCC是一种基于服务的协同过滤算法,通过Pear-SOIl相关系数计算服务之间的相似度,以服务之间的协同关系为基础提供其它服务的QoS预测。
(3)UIPCC是一种混合方法,将UPCC和IPCC的预测结果组合在一起提供更高精度的预测结果,其准确性一般有更高的准确度。
(4)PMF是一种基于概率模型的矩阵分解算法。通过联合用户和服务的概率分布建立模型。通过矩阵分解,获取用户和服务隐矩阵提供其它QoS预测。
(5)RWE是一种基于用户的随机游走模型。主要通过矩阵分解的中间结果计算用户之间相似度,在基于协同过滤的基础上提供预测。
(6)XEMF是一种基于矩阵分解的算法。主要通过矩阵分解产生用户和服务隐含矩阵,结合用户和服务初始条件提供矩阵缺失值预测,是本文提出的参照算法。
表3和表4显示了7种方法分别在RT和TP数据集上的预测精度的实验结果。其中每一行是每种预测方法MAE和NMAE指标,每一列表示不同采样率,分别在5%、10%、15%、20%采样率下进行实验。
当采样密度为5%时,基于MF算法(PMF)比基于PCC(UPCC,IPCC和UIPCC)具有更小的MAE和NAME,所以预测精度更高。同时,RWE算法的MAE值为0.5255,相对于UPCC、IPCC和UIPCC等基于相似性的协同过滤算法,预测准确度更高。同样,基于矩阵分解的方法XEMF的预测精度较PMF有提升。RWEMF算法有0.5068的MAE值和0.5591的NMAE,较其它几种预测算法有很大提升。在不同采样率10%、15%、20%下,RWEMF同样有着最小的MAE和NMAE值,因而RWEMF适用于不同的采样率情况。最后RWEMF在TP的数据集上也有着相同优越的表现,较其它算法有更低的MAE和NMAE值。因此可以验证RWEMF能适用不同数据集合。实验表明使用了随机游走方法的RWEMF提高了用户间相似度计算结果,利用矩阵分解方法的优势有效提高了预测的准确性。
4.4实验参数分析
RWEMF中TOPK、MF的隐含维度ldmf(矩阵分解的隐含维度)以及RW和MF混合系数λrumf是直接影响QoS预测精度的重要参数,下面分别对这3个参数进行讨论。
图l和图2表示调整参数topK后,RWEMF分别在RT和TP数据集上的性能表现。其中x轴表示5%、10%、15%、20%的采样密度,丫轴表示RWEMF方法的预测精度MAE。从图中可以看出,当topK=3时,RWEMF在不同采样密度下较topK为其它值时有更小的MAE值,这同样适用于RT和TP。因此,选择合适的近邻数量能使算法得到更好的预测效果。
图3、图4表示RWEMF在不同MF分解维度下运行时间和预测精度性能。其中x轴为矩阵分解时的维度,1d-mf包括5、10、15、20、25等几个分解维度。左边的丫轴表示算法的运行时间对应图中条形统计部分,右边的丫轴表示算法的MAE精度对应图中折线部分。算法比较试验在5%、10%、15%、20%采样密度下进行。首先分析图中条形统计部分,在采样密度增加时,算法运行时间也在增加;其次在ldmf算法的矩阵分解维度增加时,算法运行时间也在增加;再分析折线统计部分,折线统计结果是在同一采样密度5%下得到的。随着1dmf变化,预测算法的精度也在变化。当ldmf=15时,在RT和TP数据集上,RWEMF算法的MAE相对较小,预测精度较高。随着ldmf的变化,MAE值反而增加,说明更高的分解维度不会提高算法的预测精度,表明更高维度的分解会引入数据噪声从而影响精度。综合运行时间和预测精度,当1dmf=15时,算法相对运行更快,可实现更高的预测精度。因此,选择合适的1dmf参数是RWEMF算法高效运行的基础,需要平衡运算和预测精度之间的关系。
图5、图6表示λrumf,参数在混合RWE和MF预测中提高精度的作用。其中x轴表示λrumf,参数,其值在[0,1]之间,y轴表示预测精度MAE值。实验中选择具有代表性的低5%和高20%的采样密度进行实验。每种密度都有3种线型(RWE、XEMF和RWEMF)。很明显,XEMF的MAE是三者中最大的,RWE的MAE低于MF。使用λrumf,为0.7时RWEMF达到了MAE的最小值,此即为算法的最优预测状态。RT和TP数据集具有同样的实验效果。因此,选择合适的λrumf对RWEMF提高预测精度有重要作用。
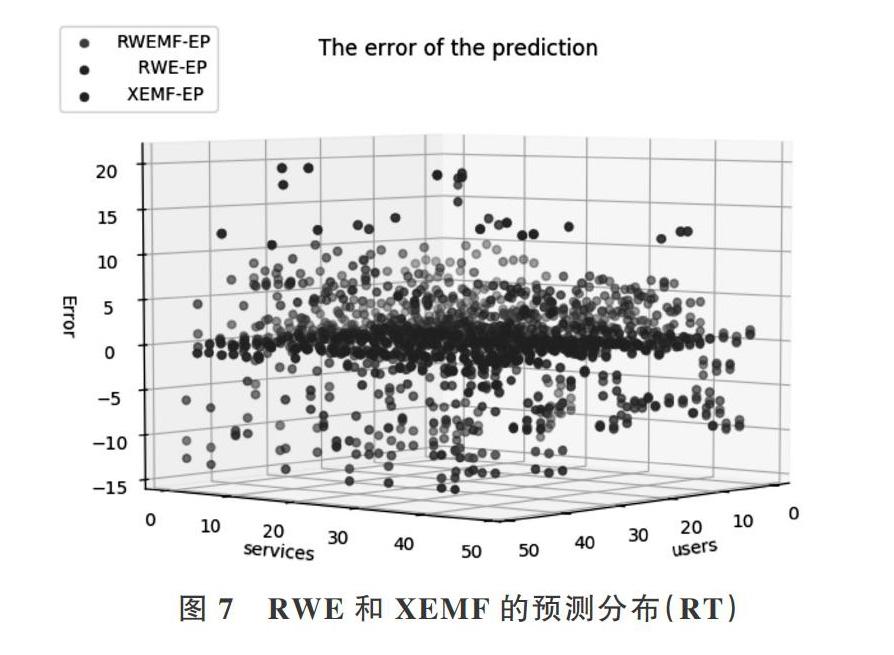
图7、图8表示在RT和TP上3种算法(RWEMF、RWE和XEMF)预测值的分布情况,其中的每个点表示此算法的預测值和实际值误差的相对位置。其中x和y轴分别代表用户和服务编号,z轴表示算法的相对误差值。图中的点经过简化处理,表示数据集上的预测相对位置。这两个图可以形象反映出3种算法的预测能力,也解释了为什么RWEMF可以有效提高预测精度的原因。RWE算法预测的点分布较为分散,在Error为-15,0,20的平面上都有聚集。分析后发现由于RWE对局部信息更加敏感,在某些位置具有较高的准确度,但在有些位置上又存在较大误差,因此它在整个数据集上具有较大的方差,表现为红色点离散度更大。XEMF预测的点聚集在靠近Error为0的平面附近,XEMF无法实现局部更高的准确性,但它的预测整体差异很小。RWEMF的点通常位于RWE和XEMF之间,且点聚集在靠近Error为0的平面附近。因此,混合算法的预测有效融合了RWE和XEMF的预测结果,在RT和TP数据集上都有良好表现。
5结语
本文针对Web服务QoS数据集在稀疏采样条件下的特点,结合现有的基于随机游走的CF和MF优点,提出了混合型预测算法RWEMF。在WS-Dream数据集上对RWEMF算法进行了验证,实验结果表明该预测方法较传统预测方法有效地提高了预测精度。通过对实验参数的进一步分析发现,相似度计算和附近邻域选择对RWEMF预测精度提高很重要。基于随机游走的CF和MF算法的融合在RT数据集上5%采样密度下的MAE为0.5068,足以体现RWEMF能有效提高Web服务QoS值预测效果。
今后将研究通过对更高精度模型的融合使Web QoS的预测准确度进一步提高。结合Web QoS数据特点,从算法角度设计运行时间少和预测精度高的Web服务预测方法,在Web服务环境中提高系统预测推荐效率。

