基于最优回归-灰色模型的走私案件预测研究
张梅美 曹金璇

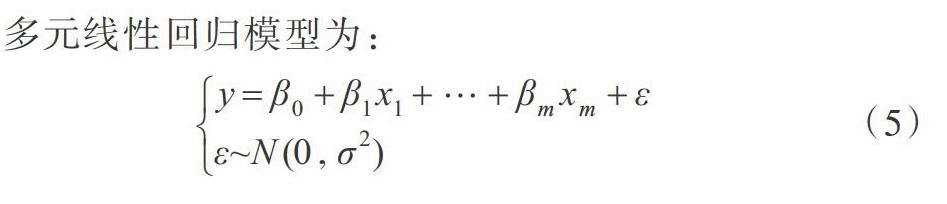

摘要:国家税收中关税占有很大比例,走私犯罪主要依靠逃避国家关税获取高额利润。以全国走私案件数为研究对象,采用回归模型对全国走私案件进行有效预测。验证结果表明:回归一灰色模型相比于单独应用回归模型方差和降低了87.67%,预测精度显著提高,预测结果具有波动性,更符合实际情况,能够为走私案件预测提供决策支持。
关键词:走私案件预测;灰色模型;回归灰色模型
DOI:10.11907/rjd k.192201
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2019)012-0069-04
0引言
税收是国家财政的重要来源,其中关税在税收中占比相当大。由于我国对外贸易的强控制、国内外同一商品的差价不断攀升,以及相关法律制度不够完善,人们一般认为走私犯罪不会对公民个人利益产生影响,因此我国走私形势相当严峻。走私犯罪大多会伴随一些其它经济犯罪,严重败坏社会风气。走私犯罪手段层出不穷,走私物品种类越来越多,在这种情况下,有效预测走私案件数量,针对未来案件发生趋势提前作好决策非常重要。在预测与预防控制方面美国有环境预防控犯罪论、社会控制犯罪论、社区警务理论等。在灰色预测模型基础上有灰色关联度组合优化模型,将两个甚至多个随时间改变的因素进行关联分析,对于交通量的预测应用灰色马尔科夫链预测模型,也有将灰色预测模型应用在人口预测中。因单一模型绝大多数情况下没有组合预测模型预测效果好,因此本文考虑组合灰色模型与回归模型进行预测。
1回归预测模型与灰色预测模型研究现状
回归分析模型和灰色理论预测模型等一些犯罪预测方法,将犯罪预测由原来的定性研究转变成为定性与定量研究相结合,使犯罪预测研究方法多样化,完善了犯罪预测体系,使预测变得更加精准、快速。
常见的回归分析预测法有:一元线性回归预测法、多元线性回归预测法和非线性回归预测法。2006年为准备北京奥运会,北京崇文区公安分局应用一元线性回归预测崇文区2005-2008年犯罪增长趋势并对相关因素进行预测。由于犯罪是由很多因素造成的,因此对于犯罪的预测更多采用多元线性回归方法。虽然对于多元线性回归研究较多,但在犯罪预测领域应用多元线性回归的却很少。由于灰色系统预测理论更注重事物的系统分析、立体思维而不是建立精确的系统模型,因此可以克服传统预测理论的一些不足。
2相关理论概述
2.1GM(1,1)模型
灰色系统是内部既包含一些已知信息也包含一些未知信息的系统,此系统可以采用一系列累加累减弱化系统的灰色不可知因素,加强已知因素对系统的影响,最终通过确定方程参数构造时间序列微分方程。此类模型的优点是对于短期预测效果明显,且不需要很多数据样本。
GM(1,1)模型用来揭示数据序列的发展变化趋势,能够通过对一些没有任何规律的原始数据进行运算得到规律较强的生成序列,而且不用考虑变化趋势与分布规律。但是灰色GM(1,1)模型的缺点是不适于长期数据预测,只能应用于中期与短期数据预测。因此考虑将回归预测模型与灰色预测模型相结合进行预测,以提高预测拟合度。
GM(1,1)模型在预测过程中存在局限。在应用GM(1,1)模型进行预测的过程中发现,模型从预测效果到拟合优度的性能都不一致,虽然灰色理论预测模型的预测结果精度与初始序列的光滑性存在一定关系,但在建立差分方程过程中不能确保拟合方程和微分方程的高度近似。
2.2回归预测模型
3回归一灰色预测模型构建与优化
目前预测犯罪数量模型很多,但在实际中有很多数据浮动范围较大,单独用回归分析模型与灰色理论分析方法都不能获得好的预测结果。为提高模型预测的准确性,本文方法为先使用回归分析模型得到回归模拟值,之后再求出残差,最终与灰色理论模型相结合,基本流程如图1所示。
开始要将初始事件序列数据进行规范化处理,之后将规范的数据分别作不同回归函数的拟合优度检验,选取相关系数最高的作为回归模型函数;随后对于选择的回归模型进行回归系数相关检验。灰色预测模型与筛选好的回归模型进行组合之前要进行准光滑性检验、准指数性检验和模型方差分析,最后得到组合预测模型。
单一预测模型较多,将几个模型组合起来能否使预测准确性提高值得研究。虽然绝大多数组合后的预测模型准确率提高很多,但是也存在一些个例。有外国学者选取14种预测模型和3003个时间序列进行研究,對样本进行任意组合,最后得出组合模型个数越多预测误差越小的结论。这是一种边际效应。单一预测模型预测误差比组合模型预测误差要大一些,但是并不显著;组合模型未必是最佳模型,然而在大量数据支撑下组合模型具有普遍优势。因此,对于预测过程中是否进行模型间的组合要看如何选择组合策略。
4应用实例分析
每一年的走私案件立案数波动较大,数据样本较少,而且有一定的随机性、模糊性。灰色预测模型在处理小数据样本、模糊数据处理上有很大优势,灰色理论模型可以在原始数据累加的过程中降低数据的随机性。表1为2003-2006年全国走私案件立案数。
在构建关于全国每年走私案件立案数模型之前,先筛选出相关系数最高的原始数据回归模型,然后对原始数据进行检验,看是否符合灰色理论预测条件,最后将回归模型与灰色预测模型组合,对预测的准确性进行评估。
图2中横轴是时间(单位:年),纵轴表示每年的走私案件立案数(单位:件)。可以看出全国走私案件立案逐年上升,但是数据存在一定的振幅,单一用回归方法预测模型或灰色理论预测都不能获得好的预测效果,因此考虑应用回归一灰色优化组合预测模型对全国走私案件立案数进行预测。
4.1回归分析
在SPSS软件中带有一些固定的函数模型,因此可以选取软件中适合的回归函数依次比较函数与原始数据的相关系数以及拟合优度,从而选取最优回归预测模型。表2列举了SPSS中选取的几个模型函数,以及各个模型函数与初始数据的相关系数和拟合优度。
4.3组合预测模型应用
由表3可知,回归模型方差比灰色模型方差小,所以在构建组合预测模型之前选择回归模型作为组合的基本模型,之后再将单一灰色预测模型平滑后的模拟值作为组合预测模型的初始值进行预测。
在前人研究中,大多数应用的是效率较高的单一预测模型。但是大量实验证明,组合预测模型准确性会高于单一预测模型,而且因为单一模型在不同时刻的预测误差不同,所以组合预测模型对于动态变化的预测效果会更好。
由表3可以看出,残差值并不均为正值,因此在带入过程中应用了符号函数sign(x)。对残差进行计算可知,单独只用回归方程进行回归模拟的回归方差和为166404.3,而回归于灰色模型组合后的方差和为20512.422,比单独用回归模型预测值方差和少了87.67%。可以看出将回归预测模型与灰色理论预测模型相组合后构成的组合模型,预测效果远好于单独使用回归模型预测以及灰色模型预测,因此回归一灰色组合模型有较好的预测性能。
5结语
本文以2003-2017年走私案件立案数为数据,分别应用单一回归模型和单一灰色模型对10年数据进行预测分析,分别计算回归模拟值、残差以及回归方差。经过比较,两个单一预测模型回归分析准确度高于灰色预测模型。因此选择回归预测模型为基础模型,选择模拟预测值为初始值,将模拟值与实际进行对比但效果不够理想。最终将回归模型与灰色预测模型组合起来形成回归一灰色预测模型,将组合后的回归一灰色模型与之前模型进行比较评估,为有效预测走私案件提供数据支持。但在实战过程中,仅仅依靠数据模型预测是不够的,预测模型只能为公安工作提供一定的技术支持,仍需结合实际情况与需求进行改进,才能更好地服务于公安工作。

